RNN Learns Suitable Hidden Dimensions with White Noise

Abstract

Neural networks need the right representations of input data to learn. Recently published in Nature Machine Intelligence, a new study examines how gradient learning shapes a fundamental property of representations in recurrent neural networks (RNNs)—their dimensionality. Through simulations and mathematical analysis, the study demonstrates how gradient descent guides RNNs to compress the dimensionality of their representations to meet task demands during training while supporting generalization to unseen examples. To achieve this, an expansion of dimensionality is needed in the early stages of training, followed by compression in the later stages. The study finds that RNNs with strong chaotic characteristics are particularly adept at learning this balance. This research not only helps clarify the benefits of appropriately initialized RNNs for training but also reveals the relationship between neural circuits in the brain and chaos. In summary, the findings show how simple gradient-based learning rules guide neural networks to produce robust representations that can solve tasks and generalize to new situations.

Research Fields: Representation Learning, Gradient Descent, Recurrent Neural Networks, Chaos, Network Dynamics

Paper Title:

Gradient-based learning drives robust representations in recurrent neural networks by balancing compression and expansion

Paper Link:

https://www.nature.com/articles/s42256-022-00498-0

1. How to Determine the Suitable Representation Dimension?

Before supervised learning, transforming raw data into suitable features is essential; this step is known as representation learning. A critical step in this process is determining the dimensionality of the data. High-dimensional representations can contain useful nonlinear combinations of features, suitable for building simple classification models, while low-dimensional representations can retain key features, allowing learning based on fewer parameters and examples, thus exhibiting better generalization ability.

Thus, a practical question arises: how to determine the suitable representation dimension? The study demonstrates that the dynamic characteristics of RNNs can produce suitable representation dimensions based on gradient descent. The specific algorithm steps are shown in Figure 1, where the input is the high-dimensional data to be classified. During the training process, the model constructs data representations using the output from the previous layer as input (attempting to construct a hyperplane that can distinguish between two classes of data). Finally, the representations from the previous nine steps are summed, and the representation model is evaluated based on the accuracy of the classification algorithm. The training of the representation model then relies on the evaluation results, using gradient descent.

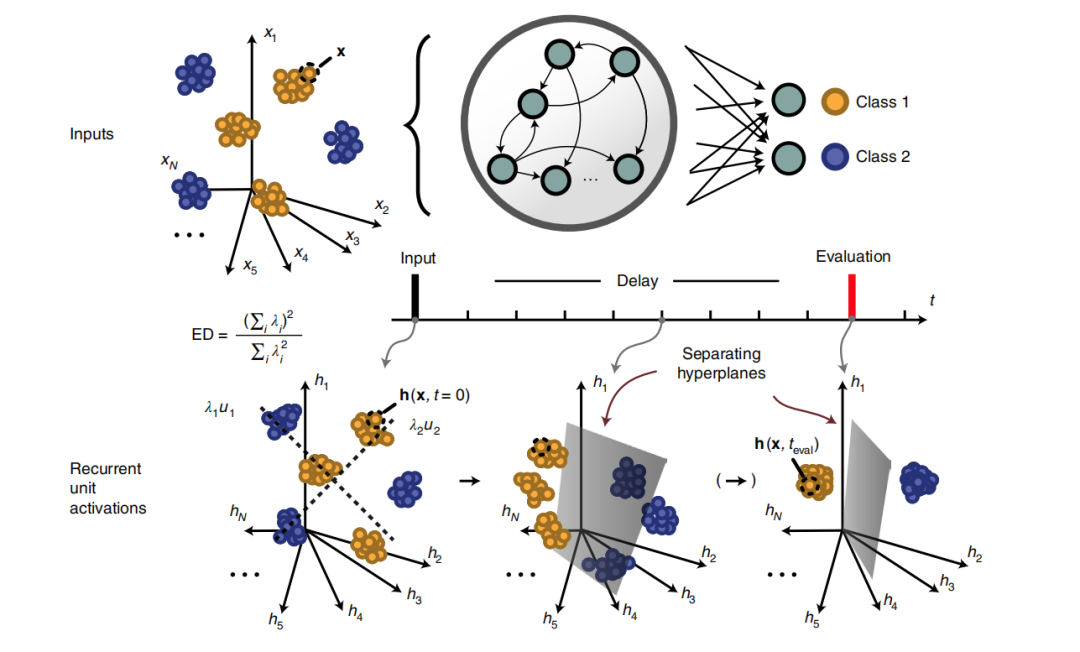
Figure 1: Task of the algorithm and illustration of using the model

2. Neural Networks and Chaos

When the hidden dimension of the known data is two-dimensional, this experiment compares RNN networks at the edge of chaos and in a strongly chaotic state, finding that networks in a strongly chaotic state achieve similar classification accuracy with less training data (Figure 2d); they can obtain suitable effective representation dimensions after training (Figure 2e). When using linear regression for classification on the representations obtained after training, the accuracy is higher (Figure 2f), and the generalization ability is better (Figure 2g).

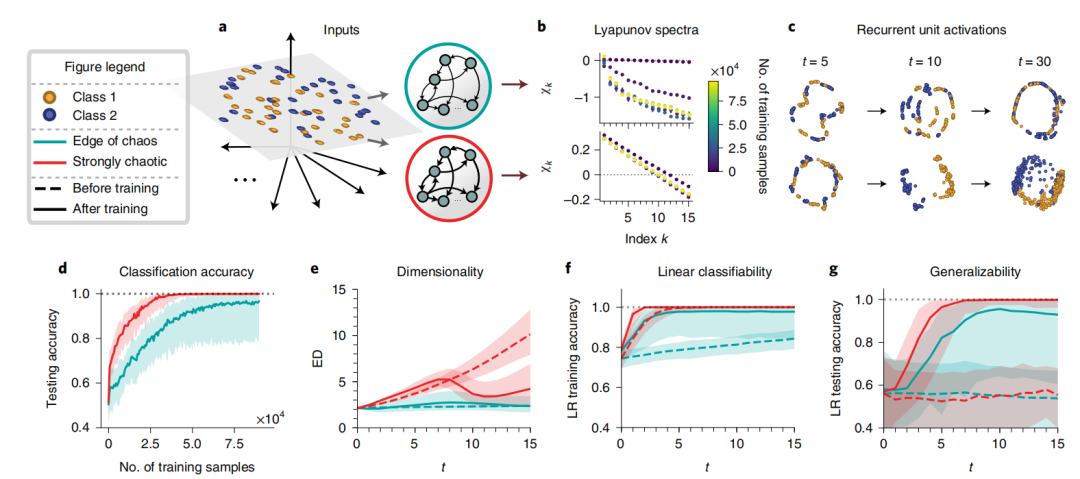
Figure 2: Dynamics and geometric properties of the learning network for two-dimensional input classification

The above data indicates that for hidden dimensions greater than or equal to two, RNNs in a strongly chaotic state can learn suitable hidden dimensions and derive representations usable for classification with linear models. Compared to RNNs at the edge of chaos, those in a strongly chaotic state perform better.

The reason RNNs can learn compressed representations may come from the formation of stable fixed points (for networks initially at the edge of chaos) or from low-dimensional chaotic attractors (for networks in a strongly chaotic state). This means that when training stable networks to learn tasks, the chaotic parts of the network will be reset in comparison before and after the training evaluation period. The former (networks at the edge of chaos) may be beneficial for long-term memory; the latter (networks from low-dimensional chaotic attractors) can be used for flexibly learning new tasks.

3. Learning Mechanism of Representation Models

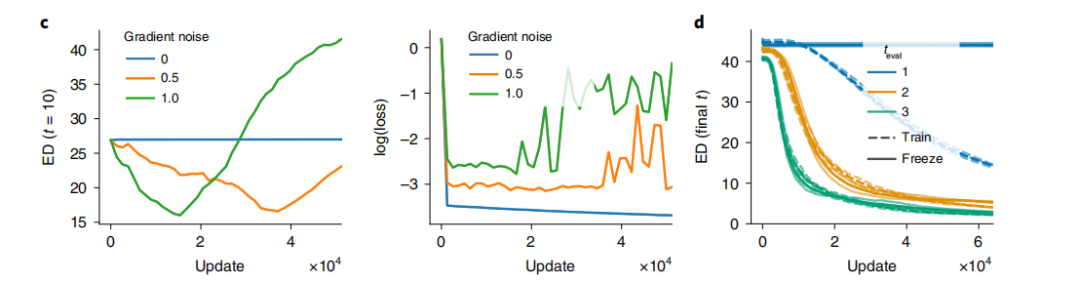
Subsequently, the evaluation metric was changed from measuring classification results using cross-entropy to measuring classification confidence using mean squared error loss. By using continuous rather than discrete evaluation metrics, the learning mechanisms of representation models can be studied. It was found that when random noise is not added to the nodes, the model does not attempt to reduce the effective dimensionality during training (Figure 3c left), but always keeps the model’s prediction error extremely low (exchanging more representations for better prediction performance). However, the model with noise will attempt to reduce the effective dimensionality, even though this leads to increased prediction error. Figure 3d shows the final effective representation dimensions at the end of training; during training, the greater the proportion of Gaussian noise added to the neuron gradients, the faster the model can learn suitable hidden dimensions.

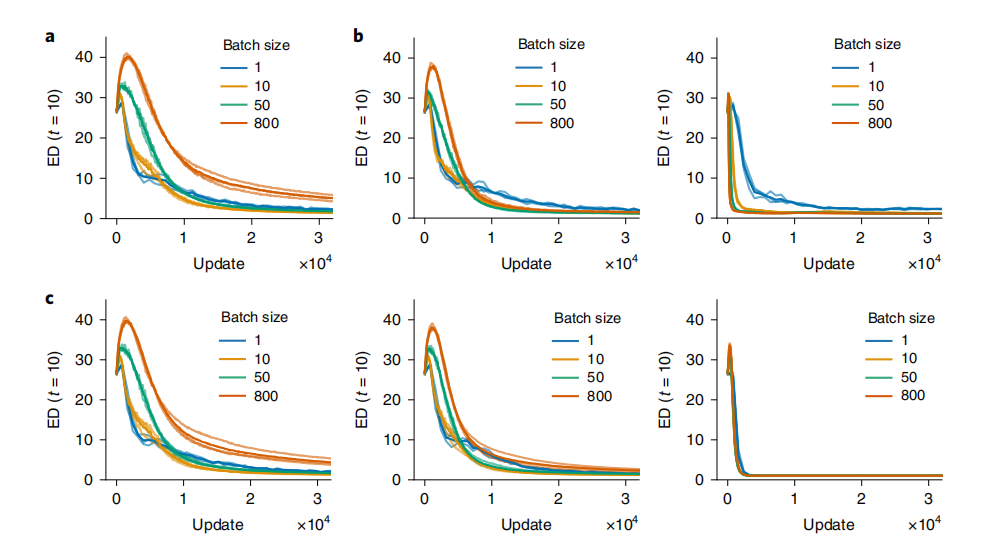
Further comparisons were made regarding the impact of different regularization methods: Figure 4a shows the dimensions learned with different batch sizes when no noise is present; the left side of Figure 4b shows the situation when Gaussian noise is added to the neuron gradients during training, while the right side shows the effect of dropout regularization with noise included; Figure 4c illustrates the cases of adding weak, moderate, and strong L2 regularization terms from left to right. It can be seen that using strong L2 regularization, as well as dropout, yields similar results, both able to learn suitable hidden dimensions in the presence of noise. This indicates that the learning mechanism of RNNs is based on random noise during the learning process.

In summary, this study points out that RNNs can learn to balance compression and chaos in representation learning in a way suitable for the task at hand, thereby obtaining suitable representation dimensions, with the driving force of the learning process coming from the noise during the neuron gradient change process. Currently, the understanding of the learning rules used by the brain is still in its early stages, and a common hypothesis is that the brain learns in a gradient descent manner. This study enhances the feasibility range of this hypothesis and proposes two potential learning mechanisms (white noise and regularization) along with corresponding validation methods.

With the development of various technical methods such as electrophysiology, network modeling, machine learning, statistical physics, and brain-like computing, our understanding of the mechanisms of interaction and connection among brain neurons, as well as functions such as consciousness, language, emotion, memory, and social behavior, is gradually deepening. The mystery of the brain’s complex systems is being unveiled. To promote communication and collaboration among researchers in neuroscience, systems science, and computer science, we have initiated the Neural Dynamics Model Reading Club.

The Intelligence Club Reading Club is a series of paper reading activities aimed at researchers, with the goal of collectively exploring a scientific topic in depth, inspiring research ideas, and promoting research collaboration. The Neural Dynamics Model Reading Club is jointly initiated by the Intelligence Club and the Tianqiao Brain Science Research Institute. It started on March 19 and takes place every Saturday afternoon from 14:00 to 16:00 (or every Friday evening from 19:00 to 21:00, depending on actual circumstances), expected to last for 10-12 weeks. During this period, discussions will focus on multi-scale modeling of neural networks and their applications in brain diseases and cognitive processes.

For more details, please see:

Neural Dynamics Model Reading Club Launch: Integrating Multidisciplinary Approaches in Computational Neuroscience