0

“How do deep learning models handle variable size inputs?”

A few days ago while studying the Flower Book, I discussed the question of “How CNN handles variable size inputs” with my colleagues. This extended to the larger question of “How do deep learning models handle variable size inputs?” because it involves some concepts that we often confuse, such as RNN units can indeed accept inputs of different lengths, but we tend to use padding during actual training; for example, CNN cannot directly handle inputs of different sizes, but after removing the fully connected layer, it can. Therefore, I would like to summarize this issue:

1. What kind of model structure can handle variable size inputs?
2. If the model can handle it, how should it be trained/predicted?
3. If the model cannot handle it, how should it be trained/predicted?

1

“What kind of network structure can handle variable size inputs?”

Directly to the conclusion (my personal summary, which may not be accurate/comprehensive, corrections are welcome):

When a certain network (layer or unit) is one of the following three situations: ①only processes local information; ②the network is non-parameterized; ③the parameter matrix is independent of the input size, this network can handle variable size inputs.

Below, I will respond to the above conclusion from several classic network structures:

CNN

First, let’s talk about CNN. The convolutional layers in CNN obtain features from the input through several kernels, each kernel slides over the entire input through a small window, so no matter how the input size changes, it is the same for the convolutional layer. So why can’t CNN directly handle images of different sizes? It is because in a typical CNN, there is usually a Dense layer, which connects to all inputs. After processing an image through convolutional and pooling layers, all units must be “flattened” and then input to the Dense layer, so the size of the image affects the dimensions input to the Dense layer, which is why CNN cannot directly handle it. However, there is a network called FCNN, or Fully Convolutional Neural Network, which is a convolutional network without Dense layers, so it can handle variable size inputs.

Another solution for CNN to handle variable size inputs is to use a special pooling layer—SSP (Spatial Pyramid Pooling), which was initially proposed by Kaiming He’s team. This pooling layer does not use a fixed-size window but has a fixed-size output. For example, regardless of the size of the input grid, a fixed output of 2×2 SSP pooling will divide this input network into 2×2 regions and then perform average or max operations to obtain a 2×2 output.

SSP and FCNN are both demonstrated in the “Flower Book”:

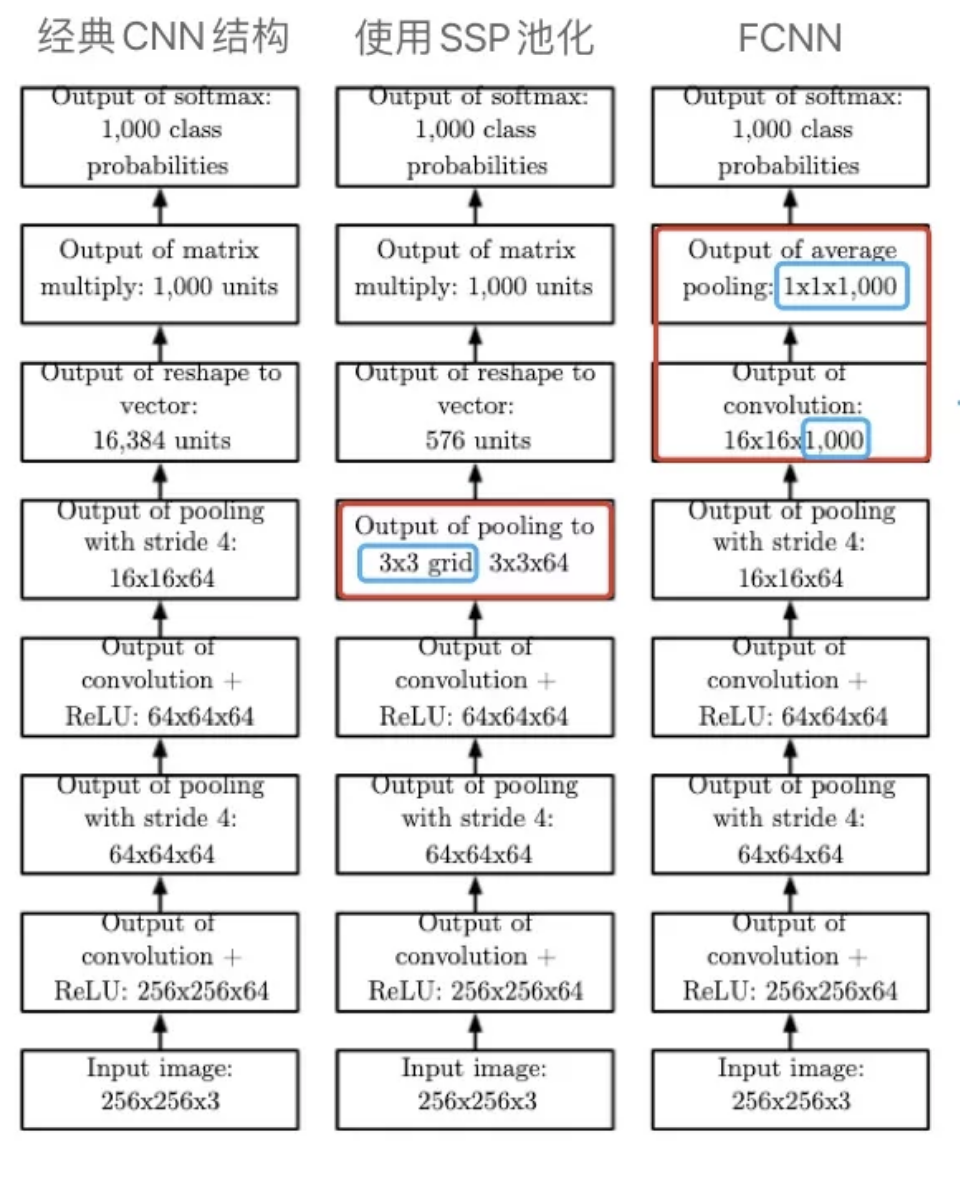
In the figure, SSP has the ability to handle variable size inputs through a pooling layer with a fixed output size. Meanwhile, FCNN removes the Dense layer, using the number of kernels to correspond to the number of categories (for example, the figure uses 1000 kernels to correspond to 1000 classes), and finally uses a global pooling—GAP (Global Average Pooling) to convert each kernel’s corresponding feature map into a single value, forming a 1000-dimensional vector that can be directly classified using softmax without using a Dense layer. Through these two special convolutional and pooling layers, FCNN also has the ability to handle variable size inputs.

RNN

Next, let’s talk about RNN. RNN consists of RNN units with shared parameters, and essentially, a layer of RNN can be seen as having only one RNN unit, which is continuously processed in a loop. Therefore, an RNN unit also processes local information—the information at the current time step. No matter how the length of the input changes, the RNN layer uses the same RNN unit. Often, we also connect a Dense layer after RNN, and then output through softmax. Does this Dense layer have an effect? The answer is no, because when using RNN, we usually only need the hidden state of the last time step, the dimension of this hidden state is set by the RNN unit, which is independent of the input length, so the interaction between this hidden state and Dense is also independent of the input dimension. For example, if the input length is l, the output dimension of the RNN unit is u, and the number of units in the Dense layer is n, then the weight matrix size in the Dense layer is u×n, which is independent of l. The weights in the RNN unit are also independent of l, only related to the input dimension at each time step, such as the dimension d of the word vector, the weight matrix size in the RNN unit is d×u. The above process can refer to the diagram below:

Transformer

Transformers can also handle variable length inputs. This issue has been discussed on Zhihu, but unfortunately, I haven’t understood it well. For example, Professor Qiu Xipeng mentioned that it is because “the weights of self-attention are dynamically generated”; I don’t understand how the weights are dynamic. For instance, Xu Tongxue said that “Transformers handle variable length data by calculating the length-related self-attention score matrix”; this is also not easy to understand at face value.

In my opinion, this has nothing to do with self-attention. Self-attention in Transformers is non-parameterized, from the input of the attention layer to the output weighted vector representation, it does not require any parameters/weights, so self-attention can naturally handle length variation inputs. The parameters in Transformers come from Dense layers, including some purely linear mapping layers (projection layer) and position-wise FFN (feed-forward layer). Understanding these Dense layer operations is key to understanding why Transformers can handle variable length inputs.

Let’s first look at the structure of Transformers:

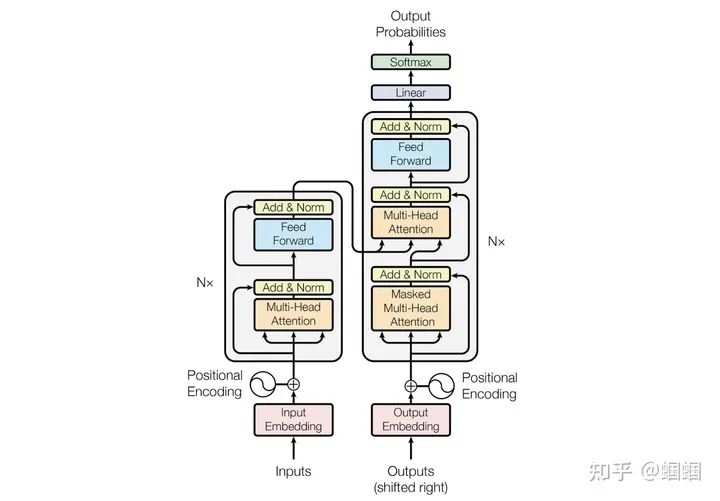
Here we focus on the encoder part, i.e., the left half. However, looking at this figure does not help us understand why it can handle length variation inputs. Therefore, I created a rough sketch (omitting multi-head, Add&Norm, and simplifying the FFN in the paper) to examine the encoder part in more detail:

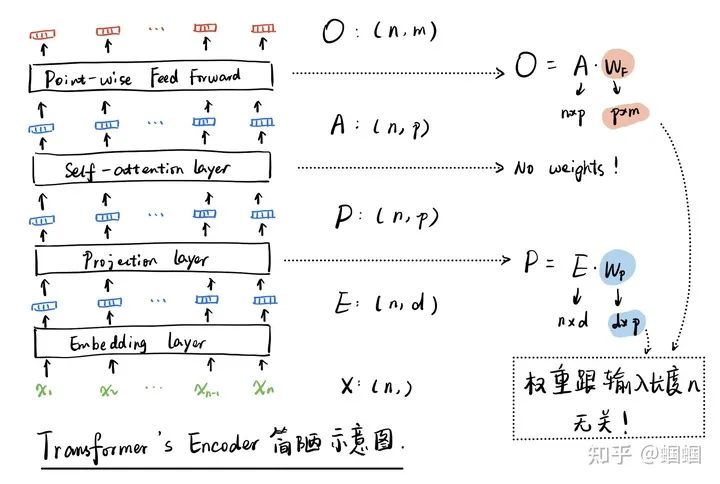
We do not need to expand on the self-attention part because it calculates attention weights between all vectors pairwise and then applies weighted sums to obtain a new set of vectors, with no parameters involved, and the dimensions and quantities of the vectors remain unchanged.

In the entire encoder, the only learnable parameters are in the projection layer and point-wise feed-forward layer, where the former is just to change the dimension of the vector of each input token (in the figure, from d to p), and the latter uses the same Dense layer for each token, converting each vector’s p dimensions to m dimensions. Thus, all parameters are independent of the sequence length n, as long as the model parameters are well learned, we can run it regardless of the sequence length n.

The only part worth examining here is the point-wise feed-forward layer, which is essentially an ordinary Dense layer, but the way it processes input is point-wise, meaning for each step in the sequence, the same operation is performed:

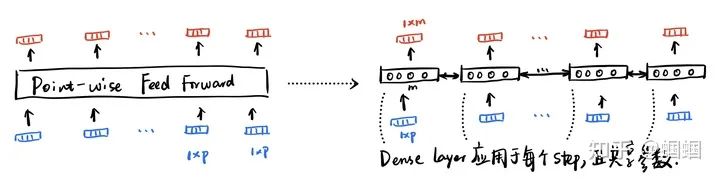
At first, I did not understand why there could still be variable length input handling with a Dense layer after the attention layer. I later realized that this is not an ordinary Dense layer, but a point-wise one, which is equivalent to a recurrent Dense layer, so it can naturally handle varying lengths.

2

“If the model can handle variable size inputs, how should it be trained and predicted?”

Through the discussion in the first part, we know what network structures can handle variable size inputs.

Taking RNN as an example, although it can handle sequences of various lengths, in training, to speed up training, we often input a batch of data into the model for computation and gradient calculation. For the same batch of data, to feed it into the network, we must organize it into matrix form, so the dimensions of each row/column in the matrix naturally need to be the same. Therefore, we must ensure that all samples in the same batch have the same length/size.

The most common method is padding, where we pad zeros to make all samples in the same batch the same length, making it easier for us to perform batch calculations. For those padded values, i.e., the zeros added, we can use a masking mechanism to prevent the model from training on these values.

In fact, research has pointed out that we can sort a batch of samples (for example, in NLP), group them, and use different max length hyperparameters for each group, which can save padding usage and improve training efficiency (I don’t know which paper this is from, I heard from others; if anyone knows, please let me know). I found a keras example code at the end of the article for reference.

Of course, if we set batch size=1, then padding is not needed, and we can happily throw in various lengths of data for training.

In prediction, if we want to perform batch predictions, we also need to use padding to fill in the gaps, while for single predictions, we can use various lengths.

3

“If the model cannot handle variable size inputs, how should it be trained and predicted?”

If it cannot handle it, we can only honestly standardize all inputs to the same size. For example, in classic CNN networks, we resize or pad all images.

Here, I need to mention the scenario of transfer learning, where we often need to directly use powerful networks trained on ImageNet for fine-tuning. The question arises: when training CNN, there must be a fixed input size established, which often does not match our usage scenario. So what to do? Anyone who has done CNN transfer learning should have experience: we need to remove all the Dense layers at the end of the other person’s network! Because as analyzed earlier, the Dense layer is the culprit that prevents CNN from handling variable size inputs. Once the Dense layer is removed, the remaining convolutional and pooling layers can happily be transferred to various different input sizes.

Another way is to modify the model structure, such as SSP and FCNN, which are modifications of classic CNNs.

During prediction in this case, we can only use a uniform input size, whether for single or batch predictions.

The above summarizes this “small problem” in deep learning—”How do deep learning models handle variable size inputs?” Although it is a small problem, a careful exploration reveals that it is quite interesting and helps us better understand the design of various model structures and the principles behind them.

Reference links:

• Discussion on Zhihu about why Transformers can handle different length data: https://www.zhihu.com/question/445895638
• Some discussions on how to implement point-wise FFN in keras:

1. https://ai.stackexchange.com/questions/15524/why-would-you-implement-the-position-wise-feed-forward-network-of-the-transforme
2. https://stackoverflow.com/questions/44611006/timedistributeddense-vs-dense-in-keras-same-number-of-parameters/44616780#44616780

• How to use masking to handle padded data in keras: https://www.tensorflow.org/guide/keras/masking_and_padding
• Setting different sequence lengths for different batches during training: https://datascience.stackexchange.com/questions/26366/training-an-rnn-with-examples-of-different-lengths-in-keras

About Us