DOI: 10.3969/j.issn.1671-7775.2023.02.003
Open Science (Resource Service) Identification Code (OSID): Citation Format: Wang Tao, He Yao. Multi-objective energy management strategy of fuel cell vehicle based on nonlinear programming and XGBoost [J]. Journal of Jiangsu University (Natural Science Edition), 2023, 44(2): 142-150.
Funding Project: National Natural Science Foundation Youth Science Foundation Project (61603120)
Wang Tao (1995—), male, from Chuzhou, Anhui, master’s student ([email protected]), mainly engaged in research on new energy vehicles.
Citation Format: Wang Tao, He Yao. Multi-objective energy management strategy of fuel cell vehicle based on nonlinear programming and XGBoost [J]. Journal of Jiangsu University (Natural Science Edition), 2023, 44(2): 142-150.
Funding Project: National Natural Science Foundation Youth Science Foundation Project (61603120)
Wang Tao (1995—), male, from Chuzhou, Anhui, master’s student ([email protected]), mainly engaged in research on new energy vehicles.
He Yao (1984—), male, from Guilin, Guangxi, associate researcher ([email protected]), mainly engaged in battery management and electric vehicle control research.
Multi-objective Energy Management Strategy of Fuel Cell Vehicle Based on Nonlinear Programming and XGBoost
(Institute of Automotive Engineering Technology, Hefei University of Technology, Hefei, Anhui 230000)
Abstract: To solve the problems of real-time and accuracy of fuel cell vehicle power distribution, an offline nonlinear programming + online XGBoost algorithm was proposed to predict fuel cell power in fuel cell vehicles. Firstly, a power system model of fuel cell hybrid vehicles was constructed, and the typical mixed driving conditions of vehicles were obtained through cluster analysis; secondly, the optimal distribution ratio of fuel cells and lithium batteries under the working condition was calculated offline using the nonlinear programming algorithm; finally, the XGBoost algorithm was trained and verified using the nonlinear programming calculation results as training data. The results show that the proposed algorithm strengthens the consideration of multi-objective optimization for the dynamic performance of fuel cell hybrid systems in current offline calculations, enhances the accuracy of online machine learning training data, and the proposed XGBoost algorithm can speed up the calculation and avoid data overfitting, achieving accurate estimation of the power of fuel cell hybrid vehicles.
Keywords: fuel cell vehicle; nonlinear programming; XGBoost ensemble learning; energy management algorithm; power distribution
Multi-objective energy management strategy of fuel cell vehicle based on nonlinear programming and XGBoost
WANG Tao,HE Yao
(Institute of Automotive Engineering Technology,Hefei University of Technology,Hefei,Anhui 230000,China)
Abstract: To solve the problems of real-time and accuracy of fuel cell vehicle power distribution in current research, the off-line nonlinear programming combining online XGBoost algorithm was used to predict the fuel cell power in fuel cell vehicles. The power system model of fuel cell hybrid vehicles was constructed, and the typically mixed driving conditions of vehicles were obtained through cluster analysis. The optimal distribution ratio of fuel cells and lithium batteries under the working condition was calculated off-line by nonlinear programming algorithm. Taking the nonlinear programming calculation results as training data, the XGBoost algorithm was used to conduct the model training verification. The comparative calculation results show that through the proposed algorithm, the multi-objective consideration of the dynamic performance optimization of fuel cell hybrid system in the current off-line calculation is strengthened, and the accuracy of the online machine learning training data is improved. The proposed XGBoost algorithm can effectively expedite the calculation speed and avoid the over-fitting of the data to realize the accurate estimation of the power of fuel cell hybrid vehicle.
Key words: fuel cell vehicle; nonlinear programming; XGBoost ensemble learning; energy management algorithm; power distribution
Classification Number: U469.7
Document Identification Code: A
Article Number: 1671-7775(2023)02-0142-09
Submission Date: 2021-12-17
Due to their high efficiency, low noise, and green emissions, fuel cell vehicles have become an important research direction in new energy vehicles. For the power energy architecture of fuel cells combined with lithium batteries, the power distribution strategy of the dual energy storage system of fuel cell vehicles has become the focus of research in recent years[1-3].
Currently, research on power distribution of fuel cell vehicles mainly focuses on optimization-based methods and machine intelligence-based methods. Optimization-based energy management distribution strategies for fuel cells can achieve accuracy and robustness in energy distribution from an optimal control perspective. The optimization-based energy distribution strategies mainly include methods based on dynamic programming, Pontryagin’s minimum principle, nonlinear programming, and model predictive control methods[4-5]. The energy management strategy based on dynamic programming starts from the global perspective of the vehicle’s driving, traversing all points in the state space to calculate the optimal solution that meets the conditions. This algorithm requires prior knowledge of the vehicle’s global working conditions, and the large calculation volume leads to its difficulty in practical application[6]. The Pontryagin’s minimum principle solves energy distribution by solving the Hamiltonian equations[7-9], which has a slightly smaller calculation volume compared to dynamic programming, but in practical applications, it requires prior knowledge of known working conditions, which limits the real-time applicability of these two algorithms. Furthermore, when analyzing the multi-objective of the fuel cell hybrid energy storage system, such as incorporating the lithium battery’s life degradation and the energy of the fuel cell unit as objective functions into the equations for constraints, the optimization algorithms based on dynamic programming and Pontryagin’s minimum principle exhibit high-dimensional characteristics, leading to a sudden increase in calculation volume[10]. Therefore, most current research uses dynamic programming and Pontryagin’s minimum principle algorithms as benchmarks for validating other algorithms and as references for strategy development. The nonlinear programming algorithm is relatively simple to model and has a smaller calculation volume, making it widely applicable.
To address the real-time issues in energy distribution of fuel cell vehicles’ hybrid energy storage systems, energy distribution strategies based on intelligent algorithms have seen significant development in recent years. Intelligent learning algorithms mainly include energy management algorithms based on neural networks[8], machine learning-based energy management algorithms, and algorithms based on neural networks. LIU Y.G. et al.[11] proposed a model based on offline Pontryagin’s minimum principle, with the degradation of lithium batteries and hydrogen consumption of fuel cells as objective functions, establishing relevant rules and conducting rule learning, which can be applied online. However, the accuracy of rule learning results still needs improvement, and the extraction of learning rules requires many preliminary preparations, while considerations for achieving multi-objectives during the simulation process are still lacking. Similarly, using machine learning algorithms, SONG K. et al.[10] proposed a modeling method for fuel cell vehicles based on deep Q-learning, categorizing different strategy gradients, and verifying the deep Q-learning strategy in multi-condition environments through the extraction of multiple working conditions. The deep Q-learning method also requires significant preliminary data processing work for multi-condition data extraction and training, and neglects considerations for multi-objectives.
In response to the aforementioned issues, the author proposes a multi-objective optimized energy management machine learning method for fuel cell hybrid vehicles[12-13]. Firstly, the modeling of the fuel cell hybrid energy storage system is introduced, detailing the framework of the power system, the modeling of the fuel cell, and the lithium battery pack, followed by the design of combined working conditions to provide a basis for subsequent offline and online calculations. The modeling process of the nonlinear programming algorithm and the objective function and function constraints of the nonlinear programming algorithm are introduced, fully considering the dynamic characteristics of fuel cells and lithium batteries to achieve accurate modeling of the fuel cell system, and the modeling process of the online XGBoost algorithm is introduced. The results of offline nonlinear programming and online XGBoost algorithms are analyzed, verifying the system stability after considering multi-objective constraints in the offline nonlinear programming algorithm, and comparing the XGBoost algorithm with the random forest algorithm to verify the advantages of the XGBoost algorithm in calculation speed and pruning optimization.
1 Hybrid Energy Storage System Modeling
1.1 Power System Framework
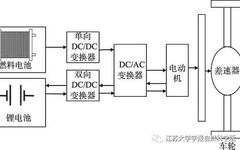
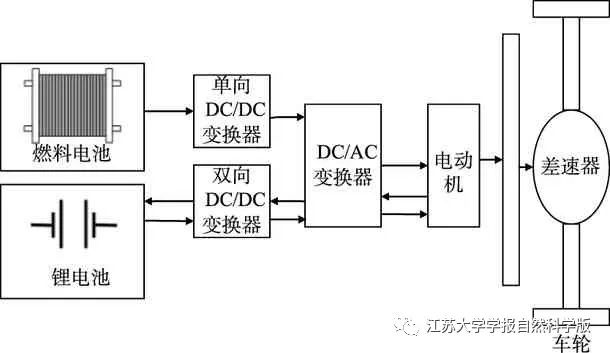
The hybrid power system is shown in Figure 1, mainly including fuel cells, lithium battery packs, DC/DC converters, DC/AC converters, and driving electric motors. The energy of the hybrid power system is transmitted to the driving electric motor through DC/AC rectification. The fuel cell module is the main module supplying energy to the power system, which has the function of charging the lithium battery and providing driving energy. It provides stable voltage to the DC bus interface through DC/DC conversion, and the lithium battery pack serves as auxiliary energy supply, bearing the role of providing peak power during vehicle acceleration and recovering braking energy.
Figure 1 Hybrid Power System Model
Analyzing the power distribution strategy of the fuel cell vehicle hybrid energy storage system first requires knowing the power demand of the vehicle. Under known working conditions, the power demand can be calculated through the vehicle dynamics model, where the vehicle driving force is
Where: mz is the total mass of the vehicle; g is the gravitational acceleration; f is the rolling resistance coefficient; CD is the air coefficient; A is the frontal area; ρ is the air density; v(t) is the vehicle speed; δ is the rotational mass coefficient.
The driving power required for the vehicle is
The demand power of the vehicle power system is
Where: ηDC/AC is the efficiency of the DC/AC converter; ηmotor is the efficiency of the motor system; ηtrans is the efficiency of the vehicle transmission system.
For simplicity, the impact of the dynamic performance of the powertrain system on modeling is not considered, thus the power modeling of the power system is simplified to
Where: Pfc is the power of the fuel cell group; ηDC/DC is the efficiency of the DC/DC converter; Pbat is the power of the lithium battery.
1.2 Fuel Cell Modeling
The fuel cell, as an energy conversion device, is adopted due to the high power density and fast start-up capability of proton exchange membrane fuel cells. The rated power is 30 kW, and a fuel cell model based on physical and empirical data is established in Simulink, providing computational parameters for nonlinear programming, ensuring that the fuel cell operates within a high-efficiency working range while ensuring good hydrogen fuel consumption during vehicle operation.
1.3 Lithium Battery Pack Modeling
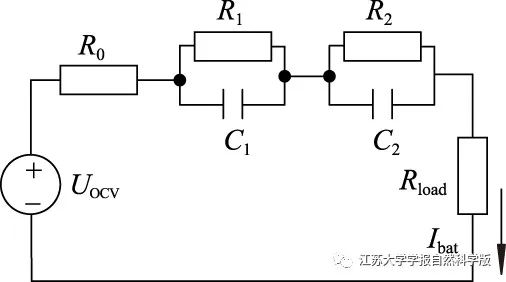
In modeling the lithium-ion battery, a second-order RC equivalent circuit model is chosen to balance battery accuracy and complexity, as shown in Figure 2.
Figure 2 Lithium-ion Battery Equivalent Circuit Model
In Figure 2: UOCV is the open-circuit voltage, which is a function of SOC; Rload is the load resistance; R0 is the internal resistance of the battery; R1, R2 are the polarization internal resistances of the battery, forming parallel RC branches with capacitors C1, C2 having different time constants. The relationship satisfied by this model is
U(t)=UOCV(SOC(t))-R1IR1(t)-R2IR2(t)-R0Ibat(t),
Where: U(t) is the terminal voltage of the battery; Ibat(t) is the loop current; IR1(t) and IR2(t) are the currents on the RC branches R1 and R2, respectively.
The expression for SOC is
Where: SOC(t0) is the initial SOC; η is the Coulomb efficiency; i(τ) is the current; Q is the total capacity of the battery.
The parameters of the lithium battery model are identified from experimental data.
1.4 Combined Working Condition Design
When a vehicle is in operation, it faces various complex working conditions. When calculating and analyzing various working conditions of the vehicle through the nonlinear programming algorithm for validation data sets for online algorithms, a large amount of working condition data is required for driving condition recognition. The standard working conditions used for testing are close to 40 types. To simplify the time and difficulty of condition calculations during modeling, clustering analysis methods are used for condition classification and recognition, and the classified working conditions are combined into a mixed condition that encompasses many working conditions. The calculation process is as follows: ① The working condition data is the speed-time relationship curve, and typical working conditions are divided using a fixed step analysis method. For the selection of vehicle driving condition parameters, the selected feature parameters include average speed, maximum speed, speed standard deviation, idle time ratio, the proportion of time from 0 to 20 km·h-1, the proportion of time from 20 to 60 km·h-1, the proportion of time greater than 60 km·h-1, constant speed cruising time ratio, maximum acceleration, maximum deceleration, and average acceleration. 24 typical working conditions are selected from ADVISOR to extract the feature parameters of each working condition; ② After obtaining the feature data for each working condition, K-means clustering divides the sample data into different clusters by minimizing the squared error, using Euclidean distance as the standard for sample classification. The calculation formula is
‖xi–xj‖=
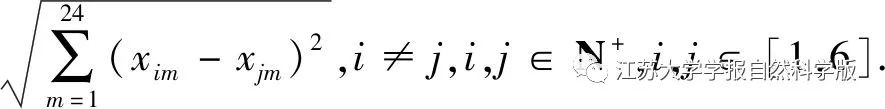 Where: xi and xj are the feature parameters of the samples.
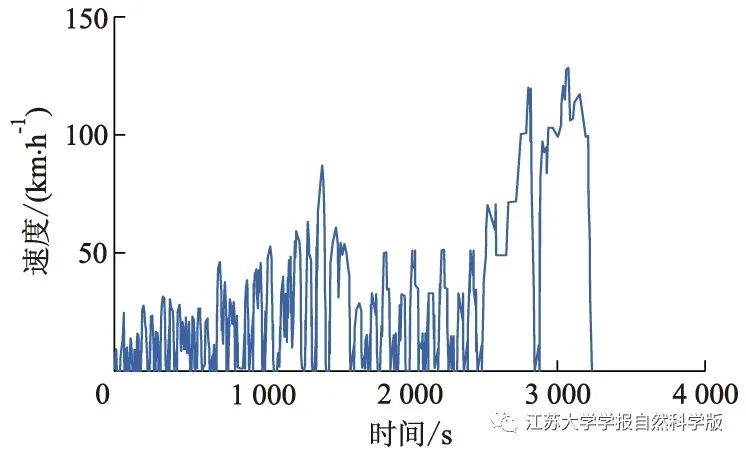
Based on the obtained clustering centers, standard working conditions are constructed, obtaining high-speed conditions, urban conditions, suburban conditions, and congested conditions, thus deriving mixed conditions suitable for validating energy management strategies. The speed curve of the mixed working condition is shown in Figure 3.
Figure 3 Speed Curve of Mixed Working Condition
Where: xi and xj are the feature parameters of the samples.
Based on the obtained clustering centers, standard working conditions are constructed, obtaining high-speed conditions, urban conditions, suburban conditions, and congested conditions, thus deriving mixed conditions suitable for validating energy management strategies. The speed curve of the mixed working condition is shown in Figure 3.
Figure 3 Speed Curve of Mixed Working Condition
2 Nonlinear Programming and XGBoost Algorithm Modeling
The control algorithm process is shown in Figure 4, extracting many typical working conditions from driving conditions, such as NEDC (New European Driving Cycle), UDDS (Urban Dynamometer Driving Schedule), and so on. These working conditions undergo clustering analysis to generate mixed working conditions, which are then fed into the nonlinear programming algorithm. Combining the objective function and constraints of nonlinear programming generates a dataset for training and verification of the XGBoost algorithm. Finally, under the influence of the XGBoost algorithm, a fuel cell vehicle power distribution prediction control algorithm is generated. In practical applications, actual driving conditions only need to be imported to complete the prediction of fuel cell vehicle power distribution. The nonlinear programming algorithm used serves as the benchmark for online energy distribution strategies, modeling the fuel cell and lithium battery packs and extracting mixed working conditions. Nonlinear programming aims at minimizing fuel consumption under mixed working conditions, with the degradation of fuel cell lifespan, fluctuations in fuel cell system power, energy fluctuations in lithium batteries (state of energy, SOE), fluctuations in lithium battery lifespan (state of power, SOP), and battery health status (state of health, SOH) as constraints, reasonably distributing the energy flow of fuel cells and lithium batteries under mixed working conditions to ensure that the power energy operates within suitable working ranges.
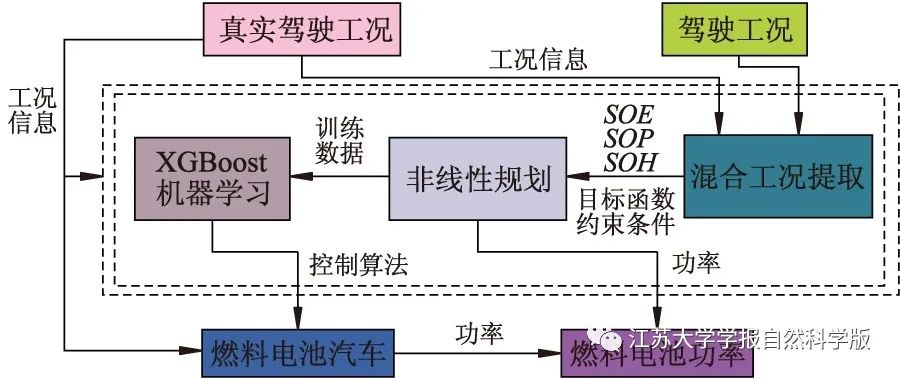 Figure 4 Control Algorithm Flowchart
Figure 4 Control Algorithm Flowchart
2.1 Nonlinear Programming Algorithm Modeling
The mathematical model of the nonlinear programming algorithm is
Where: X is a point in n-dimensional Euclidean space; f(X), gi(X), hj(X) are real-valued functions defined in the space; l1, l2 are the number of observed data.
The nonlinear programming algorithm selects the quasi-Newton method, BFGS (BROYDEN, FLETCHER, GOLDFARB, SHANNO) method, which has a small computational load per iteration while maintaining superlinear convergence, making it the most effective algorithm among quasi-Newton methods. The calculation steps of the BFGS method are as follows: ① Given an initial point x(0), allowable error ε, and the initial value of the approximate matrix Calculate the search direction
Calculate the search direction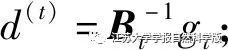 ③ Starting from the current point x(t), perform a one-dimensional search along d(t) to obtain the optimal step length λt, and update the current point x(t-1)=x(t) + λtd(t); ④ If |gt+1|<ε, stop the iteration; otherwise, proceed to step ⑤; ⑤ Calculate Δg=gt+1–gt, Δx=x(t+1)-x(t), update the approximate matrix
③ Starting from the current point x(t), perform a one-dimensional search along d(t) to obtain the optimal step length λt, and update the current point x(t-1)=x(t) + λtd(t); ④ If |gt+1|<ε, stop the iteration; otherwise, proceed to step ⑤; ⑤ Calculate Δg=gt+1–gt, Δx=x(t+1)-x(t), update the approximate matrix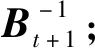 Set t=t+1, and return to step ②.
2.1.1 Nonlinear Programming Objective Function
The nonlinear programming algorithm optimizes the power distribution of fuel cells and lithium batteries. In most previous studies, the hydrogen consumption of fuel cells was set as the optimization objective. The complexity of the fuel cell and lithium battery system determines that a single objective function setting is insufficient to maximize the actual situation; therefore, when setting the objective function, it is necessary to fully consider multi-objective settings.
The energy of the fuel cell hybrid power system ultimately comes from the consumption of hydrogen fuel. The lithium battery pack is used to balance power fluctuations in the system. The charging and discharging process of the lithium battery can be equivalent to the corresponding hydrogen consumption and release. The equivalent hydrogen consumption of the lithium battery is
Where: MH2-equ is the hydrogen consumption of the fuel cell unit; T is the integration time; Ubat is the voltage of the lithium-ion battery; Istack is the current of the fuel cell; Ustack is the voltage of the fuel cell; MH2-fc is the hydrogen consumption of the fuel cell unit.
Where: P is the total power of the fuel cell; F is Faraday’s constant; Ud is the voltage of a single fuel cell.
During operation, the fuel cell vehicle’s output power is influenced by the complexity of the vehicle’s operating conditions, as changes in the motor load affect the temperature of the proton membrane and the partial pressures of hydrogen and oxygen inside the fuel cell, subsequently affecting the fuel cell’s output power. Therefore, to limit the output power of the fuel cell, a penalty function is used as the objective function for the power fluctuations of the fuel cell vehicle to constrain the power fluctuations, calculated as follows:
Cfc,load,k=α(|Pfc(k+1)-Pfc(k)|-ΔPdc,lim)2,
Where: Cfc,load,k is the power fluctuation coefficient; Pfc(k+1) is the fuel cell power at the k+1 discrete point; Pfc(k) is the fuel cell power at the k discrete point; α is the penalty coefficient; ΔPdc,lim is the maximum power change rate.
While driving, simply converting the lithium battery’s energy consumption into hydrogen fuel consumption can severely damage the lithium battery’s lifespan and charging/discharging efficiency, leading to inaccurate SOC estimates. To balance the fluctuations in SOC during vehicle operation and make SOC changes more gradual, a SOC penalty function is introduced to correct severe fluctuations in SOC, calculated as follows:
Where: x is the SOC penalty function; SOCmin, SOCmax, SOCN are the minimum, maximum, and nominal values of SOC, respectively.
Using spline curve fitting, the following relationship is obtained:
2.1.2 Nonlinear Programming Function Constraints
1) Power Demand Constraint. The demand power supplied to the motor by the hybrid power system is
Preq=PfcηDC/DC,fc+PbatηDC/DC,bat,
Where: ηDC/DC,fc and ηDC/DC,bat are the efficiencies of the DC/DC converters connecting the fuel cell and the lithium-ion battery, respectively.
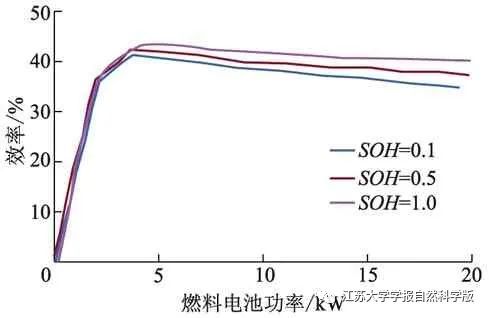
2) SOH Constraint. Rapid degradation of the fuel cell leads to changes in the health status of the fuel cell, which also affects the power distribution strategy. The degradation of the fuel cell health status mainly refers to the decrease in fuel cell power and voltage, specifically manifested as the rate of voltage drop at high or low currents. This indicates that as the degree of fuel cell degradation varies, its high-efficiency region may change. As shown in Figure 5, the output power of the fuel cell changes with its health status (SOH). When calculating the power of the fuel cell, the degradation of the fuel cell should be fully considered. Optimization control can be provided based on the decrease in efficiency, thereby utilizing unbalanced degradation to achieve higher energy efficiency throughout the fuel cell’s lifespan.
Figure 5 Fuel Cell Efficiency Under Different SOH
The coefficient of variation of system efficiency[7] is
Set t=t+1, and return to step ②.
2.1.1 Nonlinear Programming Objective Function
The nonlinear programming algorithm optimizes the power distribution of fuel cells and lithium batteries. In most previous studies, the hydrogen consumption of fuel cells was set as the optimization objective. The complexity of the fuel cell and lithium battery system determines that a single objective function setting is insufficient to maximize the actual situation; therefore, when setting the objective function, it is necessary to fully consider multi-objective settings.
The energy of the fuel cell hybrid power system ultimately comes from the consumption of hydrogen fuel. The lithium battery pack is used to balance power fluctuations in the system. The charging and discharging process of the lithium battery can be equivalent to the corresponding hydrogen consumption and release. The equivalent hydrogen consumption of the lithium battery is
Where: MH2-equ is the hydrogen consumption of the fuel cell unit; T is the integration time; Ubat is the voltage of the lithium-ion battery; Istack is the current of the fuel cell; Ustack is the voltage of the fuel cell; MH2-fc is the hydrogen consumption of the fuel cell unit.
Where: P is the total power of the fuel cell; F is Faraday’s constant; Ud is the voltage of a single fuel cell.
During operation, the fuel cell vehicle’s output power is influenced by the complexity of the vehicle’s operating conditions, as changes in the motor load affect the temperature of the proton membrane and the partial pressures of hydrogen and oxygen inside the fuel cell, subsequently affecting the fuel cell’s output power. Therefore, to limit the output power of the fuel cell, a penalty function is used as the objective function for the power fluctuations of the fuel cell vehicle to constrain the power fluctuations, calculated as follows:
Cfc,load,k=α(|Pfc(k+1)-Pfc(k)|-ΔPdc,lim)2,
Where: Cfc,load,k is the power fluctuation coefficient; Pfc(k+1) is the fuel cell power at the k+1 discrete point; Pfc(k) is the fuel cell power at the k discrete point; α is the penalty coefficient; ΔPdc,lim is the maximum power change rate.
While driving, simply converting the lithium battery’s energy consumption into hydrogen fuel consumption can severely damage the lithium battery’s lifespan and charging/discharging efficiency, leading to inaccurate SOC estimates. To balance the fluctuations in SOC during vehicle operation and make SOC changes more gradual, a SOC penalty function is introduced to correct severe fluctuations in SOC, calculated as follows:
Where: x is the SOC penalty function; SOCmin, SOCmax, SOCN are the minimum, maximum, and nominal values of SOC, respectively.
Using spline curve fitting, the following relationship is obtained:
2.1.2 Nonlinear Programming Function Constraints
1) Power Demand Constraint. The demand power supplied to the motor by the hybrid power system is
Preq=PfcηDC/DC,fc+PbatηDC/DC,bat,
Where: ηDC/DC,fc and ηDC/DC,bat are the efficiencies of the DC/DC converters connecting the fuel cell and the lithium-ion battery, respectively.
2) SOH Constraint. Rapid degradation of the fuel cell leads to changes in the health status of the fuel cell, which also affects the power distribution strategy. The degradation of the fuel cell health status mainly refers to the decrease in fuel cell power and voltage, specifically manifested as the rate of voltage drop at high or low currents. This indicates that as the degree of fuel cell degradation varies, its high-efficiency region may change. As shown in Figure 5, the output power of the fuel cell changes with its health status (SOH). When calculating the power of the fuel cell, the degradation of the fuel cell should be fully considered. Optimization control can be provided based on the decrease in efficiency, thereby utilizing unbalanced degradation to achieve higher energy efficiency throughout the fuel cell’s lifespan.
Figure 5 Fuel Cell Efficiency Under Different SOH
The coefficient of variation of system efficiency[7] is
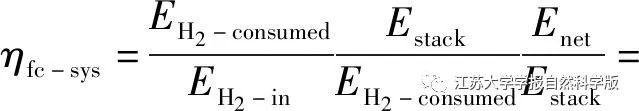 ηfuelηconvηelec=D(SOH,Pfc),
Where: EH2-consumed is the chemical energy of hydrogen consumed in the electrochemical reaction of the fuel cell; EH2-in is the input hydrogen energy; Estack is the electrical energy produced by the fuel cell stack; Enet is the output hydrogen energy.
The influence of the above fuel cell SOH on fuel cell efficiency mainly occurs through current density. Operating the fuel cell unit at the current corresponding to the tail of the polarization curve will lead to uneven current density distribution in the fuel cell, thus it is necessary to constrain the allowable range of current density of the fuel cell, as well as to impose constraints based on the operating region of the fuel cell efficiency curve:
ifc,pol,min≤ifc≤ifc,pol,max,
ifc,efficiency,min≤if≤ifc,efficiency,max,
Where: ifc is the current density of the fuel cell; ifc,pol,min is the minimum current density determined by the polarization curve; ifc,pol,max is the maximum current density determined by the polarization curve; ifc,efficiency,min is the minimum efficiency corresponding current density of the fuel cell; ifc,efficiency,max is the maximum efficiency corresponding current density of the fuel cell.
The power density begins to decline on the right side of the maximum power point, and its operational efficiency decreases. In actual operation, the fuel cell should be avoided from operating in this region. The constraints on fuel cell current density can be obtained from the fuel cell power density curve:
Where: ifc,pwr,max is the maximum current density corresponding to the fuel cell’s maximum power density.
The voltage of the fuel cell has a very close coupling relationship with the current, and compared to lithium batteries, the output characteristics of fuel cells are soft, with more noticeable voltage changes. The current density constraint of the fuel cell is obtained through the Nernst equation of the fuel cell:
Where: ifc,vol,max is the maximum current density of the fuel cell calculated based on the voltage constraint.
3) SOP Constraint. To ensure the lifespan of the lithium battery and prevent overcharging and over-discharging, the SOP constraint must be considered when predicting the charging and discharging capacity of the battery. SOP is an important indicator for predicting the maximum charging and discharging power of the battery.
The estimation method based on battery parameter constraints considers the impact of the battery’s self-constraints on peak power. The expression is as follows:
Where: Pb,min and Pb,max are the minimum charging power and maximum discharging power, respectively; Pb,min and Pb,max are the cutoff powers for charging and discharging; Upxk is the voltage; imin and imax are the minimum charging current and maximum discharging current, respectively.
4) SOE Constraint. In fuel cell vehicles, the lithium battery serves as an auxiliary energy supply, responsible for peak shaving and filling during braking and starting. The dynamic performance of the lithium battery is crucial for the entire fuel cell hybrid energy storage system, and the battery SOE serves as an energy evaluation index for the lithium battery. It is essential to constrain the SOE of the lithium battery to ensure its energy range, thus ensuring the working performance and lifespan of the lithium battery. The SOE of a single battery unit is defined as follows:
Where: SOE(t0) is the initial SOE; η is the energy efficiency; E is the rated energy of the battery.
It is necessary to ensure that the SOE of the lithium-ion battery remains within an appropriate range during operation. The constraints on SOE are as follows:
Where: SOEmin and SOEmax are the minimum and maximum limits of SOE, respectively.
The methods above have established the objective function and function constraints for the nonlinear programming of the fuel cell and lithium battery pack. The model of the nonlinear programming algorithm can be established in MATLAB to calculate the results.
ηfuelηconvηelec=D(SOH,Pfc),
Where: EH2-consumed is the chemical energy of hydrogen consumed in the electrochemical reaction of the fuel cell; EH2-in is the input hydrogen energy; Estack is the electrical energy produced by the fuel cell stack; Enet is the output hydrogen energy.
The influence of the above fuel cell SOH on fuel cell efficiency mainly occurs through current density. Operating the fuel cell unit at the current corresponding to the tail of the polarization curve will lead to uneven current density distribution in the fuel cell, thus it is necessary to constrain the allowable range of current density of the fuel cell, as well as to impose constraints based on the operating region of the fuel cell efficiency curve:
ifc,pol,min≤ifc≤ifc,pol,max,
ifc,efficiency,min≤if≤ifc,efficiency,max,
Where: ifc is the current density of the fuel cell; ifc,pol,min is the minimum current density determined by the polarization curve; ifc,pol,max is the maximum current density determined by the polarization curve; ifc,efficiency,min is the minimum efficiency corresponding current density of the fuel cell; ifc,efficiency,max is the maximum efficiency corresponding current density of the fuel cell.
The power density begins to decline on the right side of the maximum power point, and its operational efficiency decreases. In actual operation, the fuel cell should be avoided from operating in this region. The constraints on fuel cell current density can be obtained from the fuel cell power density curve:
Where: ifc,pwr,max is the maximum current density corresponding to the fuel cell’s maximum power density.
The voltage of the fuel cell has a very close coupling relationship with the current, and compared to lithium batteries, the output characteristics of fuel cells are soft, with more noticeable voltage changes. The current density constraint of the fuel cell is obtained through the Nernst equation of the fuel cell:
Where: ifc,vol,max is the maximum current density of the fuel cell calculated based on the voltage constraint.
3) SOP Constraint. To ensure the lifespan of the lithium battery and prevent overcharging and over-discharging, the SOP constraint must be considered when predicting the charging and discharging capacity of the battery. SOP is an important indicator for predicting the maximum charging and discharging power of the battery.
The estimation method based on battery parameter constraints considers the impact of the battery’s self-constraints on peak power. The expression is as follows:
Where: Pb,min and Pb,max are the minimum charging power and maximum discharging power, respectively; Pb,min and Pb,max are the cutoff powers for charging and discharging; Upxk is the voltage; imin and imax are the minimum charging current and maximum discharging current, respectively.
4) SOE Constraint. In fuel cell vehicles, the lithium battery serves as an auxiliary energy supply, responsible for peak shaving and filling during braking and starting. The dynamic performance of the lithium battery is crucial for the entire fuel cell hybrid energy storage system, and the battery SOE serves as an energy evaluation index for the lithium battery. It is essential to constrain the SOE of the lithium battery to ensure its energy range, thus ensuring the working performance and lifespan of the lithium battery. The SOE of a single battery unit is defined as follows:
Where: SOE(t0) is the initial SOE; η is the energy efficiency; E is the rated energy of the battery.
It is necessary to ensure that the SOE of the lithium-ion battery remains within an appropriate range during operation. The constraints on SOE are as follows:
Where: SOEmin and SOEmax are the minimum and maximum limits of SOE, respectively.
The methods above have established the objective function and function constraints for the nonlinear programming of the fuel cell and lithium battery pack. The model of the nonlinear programming algorithm can be established in MATLAB to calculate the results.
2.2 Online XGBoost Algorithm Modeling
Assuming that the model established by the nonlinear optimization algorithm is accurate, the data obtained from the nonlinear programming algorithm can be used to calculate the test, training, and prediction data required for the machine learning algorithm, and this data is used to verify the applicability of the XGBoost algorithm in predicting fuel cell vehicle power distribution. The analysis of the XGBoost algorithm modeling is as follows.
Currently, machine learning algorithms applied to fuel cell vehicles include rule learning-based algorithms and deep reinforcement learning-based methods. These methods face overfitting issues in practical applications, necessitating pruning of repeated increments to extract hidden rules, and the calculation speed needs improvement. The XGBoost algorithm, being the most widely used ensemble learning algorithm today, is considered for regression prediction of energy in the fuel cell hybrid energy storage system due to its extremely high computation speed and excellent ability to prevent overfitting. A fuel cell vehicle energy model is constructed to establish the mapping relationship between fuel cell power and vehicle working conditions. The mathematical model of the XGBoost algorithm is as follows:
First, obtain the dataset from the offline nonlinear programming:
Dataset={(xi,yi)∣,i=1,2,…,n,xi∈Rm,yi∈R}.
In this dataset, there are m features and n training samples, where m is the working conditions and driving features obtained from the offline nonlinear programming design. The selected feature parameters include speed conditions, acceleration, braking deceleration, lithium battery SOC, polarization voltage curve, and fuel cell SOH. yi is the corresponding fuel cell power value for the ith sample, and the relationship between the output value yi of the decision tree and the number of decision trees is
Where: yi is the predicted value; K is the number of trees; f is a sub-function of F, F={f(x)=wq(x)} (q(x):w∈R), representing the possible regression tree set, q(x) is the mapping of the sample decision tree leaf node numbers in the dataset, representing the tree structure, and w is the output value of the decision tree.
To minimize the loss error, a regularization part is introduced, and the expression of the objective function is
Where: 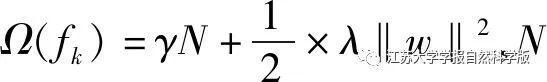 is the loss function;
is the loss function; 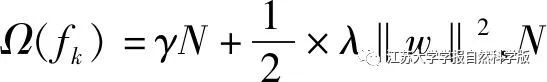 is the number of leaf nodes of the regression tree, γ is the number of leaf nodes, and λ is the regularization term penalty coefficient.
XGBoost cannot perform traditional optimization in Euclidean space but can use additional training to perform t iterations. After t iterations, the fitting residual of XGBoost is substituted into formula (26) and undergoes second-order Taylor expansion, obtaining the new objective function as
Where: gi is the derivative of the loss function.
Let Ij={i|q(xi)=j} be the sample set of decision tree nodes, combining formulas (26) and (27) yields the iterative function of XGBoost in an additive manner:
Under the condition that the tree structure is determined, the extreme points are solved by setting the first derivative to zero, yielding
Substituting the above results back into the objective function yields the scoring function:
This function adopts a greedy algorithm, continuously extending from the leaf nodes of the regression tree to the left and right, adding 2 instance sets as new objective functions IL and IR. The solving process involves summing the current IL and IR, subtracting the previous objective function to obtain the branch gain, which is
By continuously iterating and pruning, a continuous tree structure is grown, optimizing the entire model.
is the number of leaf nodes of the regression tree, γ is the number of leaf nodes, and λ is the regularization term penalty coefficient.
XGBoost cannot perform traditional optimization in Euclidean space but can use additional training to perform t iterations. After t iterations, the fitting residual of XGBoost is substituted into formula (26) and undergoes second-order Taylor expansion, obtaining the new objective function as
Where: gi is the derivative of the loss function.
Let Ij={i|q(xi)=j} be the sample set of decision tree nodes, combining formulas (26) and (27) yields the iterative function of XGBoost in an additive manner:
Under the condition that the tree structure is determined, the extreme points are solved by setting the first derivative to zero, yielding
Substituting the above results back into the objective function yields the scoring function:
This function adopts a greedy algorithm, continuously extending from the leaf nodes of the regression tree to the left and right, adding 2 instance sets as new objective functions IL and IR. The solving process involves summing the current IL and IR, subtracting the previous objective function to obtain the branch gain, which is
By continuously iterating and pruning, a continuous tree structure is grown, optimizing the entire model.
3 Algorithm Results and Analysis
3.1 Nonlinear Programming Result Analysis
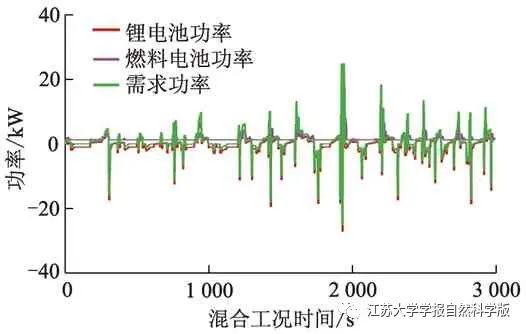
Based on the established fuel cell hybrid vehicle model and designed mixed working conditions, the power distribution results of the fuel cell hybrid storage vehicle calculated by the nonlinear programming algorithm are shown in Figure 6.
Figure 6 Nonlinear Programming Power Calculation Results
This mixed working condition combines urban, suburban, and highway conditions. In the first 1500 seconds, it mainly focuses on suburban conditions, where the vehicle’s demand power changes relatively smoothly, and all constraint conditions are met. The lithium battery, as auxiliary energy, demonstrates good power tracking characteristics. Due to the fewer instances of rapid acceleration and braking in suburban conditions, the power fluctuations of the fuel cell are small. However, in the situations around 1400 seconds, 2000 seconds, and later, as the vehicle enters urban areas and highways, and rapid acceleration and braking situations increase, the fuel cell participates more in power supply under the influence of the nonlinear programming algorithm, leading to larger fluctuations in fuel cell power. However, due to the constraints of SOH and power fluctuation constraints, the power fluctuations of the fuel cell remain within a small range, with the priority of the health status of the fuel cell being higher than that of hydrogen consumption. From Figure 6, it can be seen that the nonlinear programming planned curve shows smaller overall power fluctuations compared to the rule-based power curve, except for a few large demand power points with significant fluctuations.
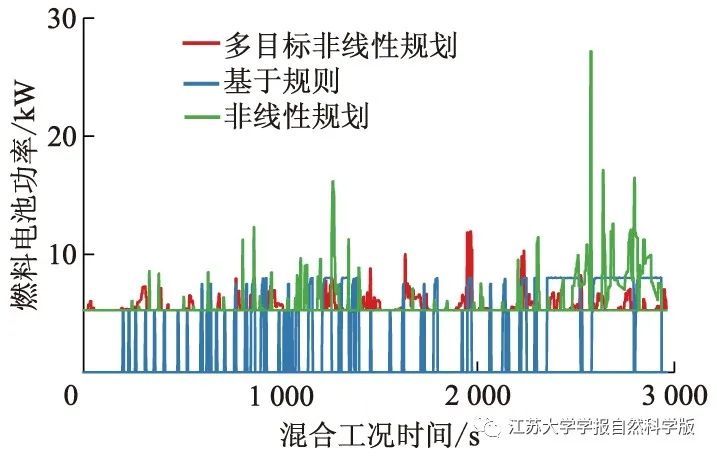
To compare the effect of adding multi-objective constraints in the nonlinear programming algorithm on improving the dynamic performance of the fuel cell, the rule-based algorithm, the nonlinear programming algorithm without multi-objective constraints, and the nonlinear programming algorithm with multi-objective constraints are selected for comparison, with results shown in Figure 7. The power of the fuel cell based on the rule changes under the set rules, showing a larger variation. The nonlinear programming algorithm sets the minimum power of the fuel cell at 3100 W. Under complex working conditions, the fuel cell operates continuously, except when charging the lithium battery during vehicle acceleration, it also outputs power during braking to ensure that the lithium battery has a high power reserve.
Figure 7 Comparison of Fuel Cell Power Under Different Constraints
From Figure 7, it can be seen that the power fluctuations under multi-objective nonlinear programming constraints are smaller. The main reason is that the nonlinear programming objective function incorporates a penalty function for power fluctuations and includes constraints on the health status of the fuel cell.
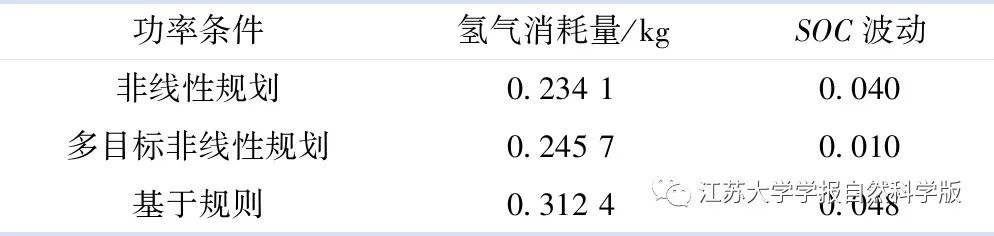
The comparison of SOC of the lithium battery under different constraints is shown in Figure 8. As the nonlinear programming sets the minimum power of the fuel cell at a certain value, both the nonlinear and multi-objective nonlinear programming approaches show a certain degree of increase in the SOC of the lithium battery. Overall, the SOC fluctuations of these two approaches are relatively small, which is attributed to the nonlinear programming algorithm’s ability to achieve better power tracking, and on the other hand, the effect of the multi-objective constraint SOC penalty function limits large fluctuations in SOC. Combined with the hydrogen consumption under the multi-objective nonlinear programming shown in Table 1, nonlinear programming can reduce hydrogen consumption over the entire working condition cycle. The difference in hydrogen consumption between nonlinear programming + multi-objective and nonlinear programming is not significant, but the effect of the SOC fluctuation constraint is very evident. If the goal is solely to minimize hydrogen consumption without considering the lifespan constraints of the fuel cell, the hydrogen consumption would be even lower. To some extent, sacrificing some economic efficiency to pursue the overall lifespan of the fuel cell is acceptable.
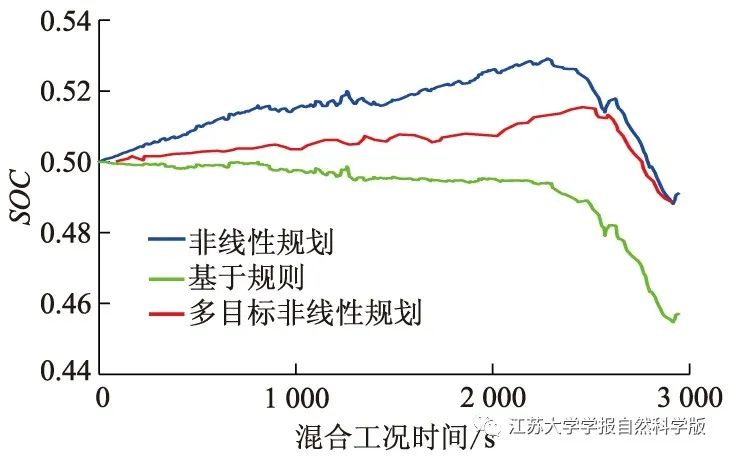 Figure 8 Comparison of Lithium Battery SOC Under Different Constraints
Table 1 Comparison of Hydrogen Consumption and SOC Fluctuations Under Different Conditions
In summary, the nonlinear programming algorithm with multi-objective constraints demonstrates better performance in maintaining the lifespan of the hybrid power system and accurately calculating the power distribution of the fuel cell hybrid power system. Therefore, the power distribution results calculated can be used in the model data of the XGBoost algorithm.
Figure 8 Comparison of Lithium Battery SOC Under Different Constraints
Table 1 Comparison of Hydrogen Consumption and SOC Fluctuations Under Different Conditions
In summary, the nonlinear programming algorithm with multi-objective constraints demonstrates better performance in maintaining the lifespan of the hybrid power system and accurately calculating the power distribution of the fuel cell hybrid power system. Therefore, the power distribution results calculated can be used in the model data of the XGBoost algorithm.
3.2 XGBoost Algorithm Result Analysis
Using the power distribution results obtained from the previous nonlinear programming algorithm, the calculated mixed condition data, such as vehicle acceleration, maximum acceleration, braking deceleration, fuel cell voltage data during vehicle operation, and fuel cell SOH, are input as feature data for the machine learning algorithm, with fuel cell power as the output. The XGBoost algorithm is employed for machine learning modeling to estimate the power distribution of the fuel cell, using 70% of the dataset as the training set and 30% as the test set. To validate the accuracy of the proposed XGBoost algorithm and its handling of overfitting in model training, a comparison is made with the commonly used random forest algorithm in regression predictions. To compare the prediction accuracy of the two algorithms, three evaluation metrics are selected: computation time, maximum error (ME), and coefficient of determination (R2).
The coefficient of determination is
Where: 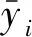 is the average of the sample data.
R2 closer to 1 indicates a higher degree of fit, while closer to 0 indicates a lower degree of fit. The comparison of different machine learning algorithms is shown in Table 2. The overall performance of the XGBoost algorithm is superior to that of the random forest algorithm, with the maximum error reduced by 28.8%, the coefficient of determination increased by 8.3%, and computation time accelerated by 62.9%. The acceleration of computation time will significantly enhance the real-time application of this model.
Table 2 Comparison of Different Machine Learning Algorithms
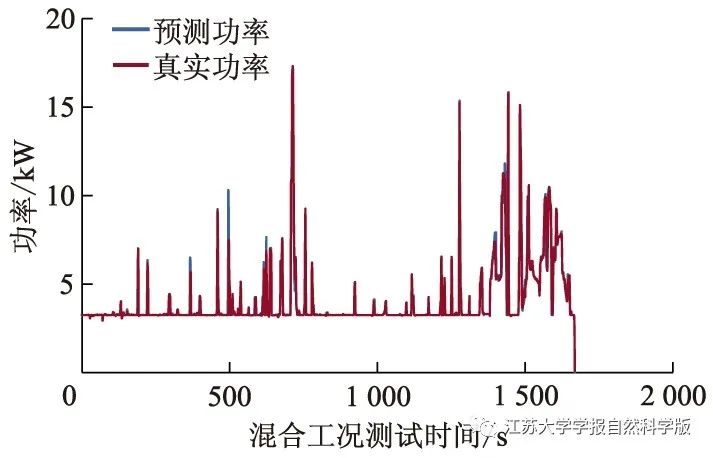
For power, the predicted results of the two algorithms are shown in Figures 9 and 10. The predicted values of the two algorithms fit well with the actual values, demonstrating good regression prediction capabilities. The fit of the XGBoost algorithm is better, with the predicted values of the random forest algorithm significantly deviating from the actual values at the tail end of the sampling points, while XGBoost can predict well. This is primarily due to the second-order Taylor expansion of the loss function in the XGBoost algorithm, which helps avoid data overfitting.
Figure 9 Random Forest Algorithm Prediction Results
Figure 10 XGBoost Algorithm Prediction Results
is the average of the sample data.
R2 closer to 1 indicates a higher degree of fit, while closer to 0 indicates a lower degree of fit. The comparison of different machine learning algorithms is shown in Table 2. The overall performance of the XGBoost algorithm is superior to that of the random forest algorithm, with the maximum error reduced by 28.8%, the coefficient of determination increased by 8.3%, and computation time accelerated by 62.9%. The acceleration of computation time will significantly enhance the real-time application of this model.
Table 2 Comparison of Different Machine Learning Algorithms
For power, the predicted results of the two algorithms are shown in Figures 9 and 10. The predicted values of the two algorithms fit well with the actual values, demonstrating good regression prediction capabilities. The fit of the XGBoost algorithm is better, with the predicted values of the random forest algorithm significantly deviating from the actual values at the tail end of the sampling points, while XGBoost can predict well. This is primarily due to the second-order Taylor expansion of the loss function in the XGBoost algorithm, which helps avoid data overfitting.
Figure 9 Random Forest Algorithm Prediction Results
Figure 10 XGBoost Algorithm Prediction Results
4 Conclusion
To address the issues of real-time and accuracy of offline calculation results when using machine learning algorithms to calculate power distribution in fuel cell vehicles, as well as the computation speed and overfitting issues in using online machine learning algorithms for fuel cell power distribution prediction, an offline nonlinear programming + online XGBoost algorithm is proposed for predicting fuel cells in fuel cell vehicles. The nonlinear programming algorithm considers multiple constraints of fuel cells and lithium battery packs, incorporating the fuel cell SOH, lithium battery SOE, and SOP as system constraints, while adding penalty functions to the objective function to establish an accurate model of the hybrid power system. Subsequently, the advanced machine learning algorithm XGBoost is utilized to address the computation speed and overfitting issues of machine learning algorithms. The overall performance of the proposed machine learning algorithm surpasses that of the random forest algorithm, with the maximum error reduced by 28.8%, and the computation time accelerated by 62.9%. By enhancing the consideration of multi-objective optimization for the dynamic performance of the fuel cell hybrid power system in current offline calculations, the accuracy of the online machine learning training data is improved, enabling precise estimation of the power of fuel cell hybrid vehicles.
[1] Wang Q, Li D G, Miao H C. Research on energy management strategy of fuel cell vehicle based on fuzzy logic control [J]. Automotive Engineering, 2019, 41(12): 1347-1355.
WANG Q, LI D G, MIAO H C. Research on energy management strategy of fuel cell vehicle based on fuzzy logic control [J]. Automotive Engineering, 2019, 41(12): 1347-1355.(in Chinese)
[2] XIANG C L, DING F, WANG W D, et al. Energy management of a dual-mode power-split hybrid electric vehicle based on velocity prediction and nonlinear model predictive control [J]. Applied Energy, 2017, 189: 640-653.
[3] WANG Y J, SUN Z D, CHEN Z H. Development of energy management system based on a rule-based power distribution strategy for hybrid power sources [J]. Energy, 2019, 175: 1055-1066.
[4] LEI Z Z, CHENG D, LIU Y G, et al. A dynamic control strategy for hybrid electric vehicles based on parameter optimization for multiple driving cycles and driving pattern recognition [J]. Energies, doi:10.3390/en10010054.
[5] ZHANG S, XIONG R. Adaptive energy management of a plug-in hybrid electric vehicle based on driving pattern recognition and dynamic programming [J]. Applied Energy, 2015, 155: 68-78.
[6] XIE S B, HU X S, XIN Z K, et al. Pontryagin’s minimum principle based model predictive control of energy management for a plug-in hybrid electric bus [J]. Applied Energy, 2019, 236: 893-905.
[7] YUAN Z, TENG L, SUN F C, et al. Comparative study of dynamic programming and Pontryagin’s minimum principle on energy management for a parallel hybrid electric vehicle [J]. Energies, 2013, 6(4): 2305-2318.
[8] BAMBANG A, ROHMAN A S, DRONKERS C J, et al. Energy management of fuel cell/battery/supercapacitor hybrid power sources using model predictive control [J]. IEEE Transactions on Industrial Informatics, 2014, 10(4): 1992-2002.
[9] ZHOU W, YANG L, CAI Y S, et al. Dynamic programming for new energy vehicles based on their work modes part II: fuel cell electric vehicles [J]. Journal of Power Sources, 2018, 407: 92-104.
[10] SONG K, DING Y H, HU X, et al. Degradation adaptive energy management strategy using fuel cell state-of-health for fuel economy improvement of hybrid electric vehicle [J]. Applied Energy, doi:10.1016/j.apenergy.2020.116413.
[11] LIU Y G, LIU J J, ZHANG Y J, et al. Rule learning based energy management strategy of fuel cell hybrid vehicles considering multi-objective optimization [J]. Energy, doi:10.1016/j.energy.2020.118212.
[12] Hu Yue. Research on control system design and energy management strategy of hybrid electric vehicles [D]. Beijing: University of Chinese Academy of Sciences, 2018.
[13] LI Wei, ZHENG Chunhua, XU Dezhou. Research on energy management strategy of fuel cell hybrid vehicles based on deep reinforcement learning [J]. Journal of Integration Technology, 2021, 10(3): 47-60.


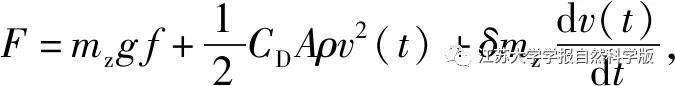
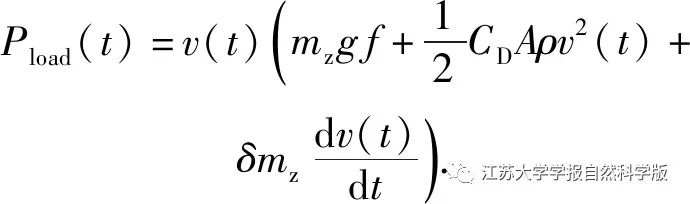
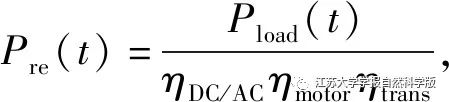
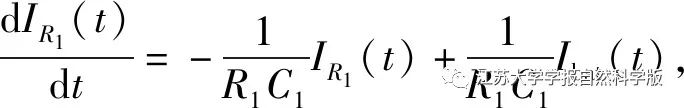
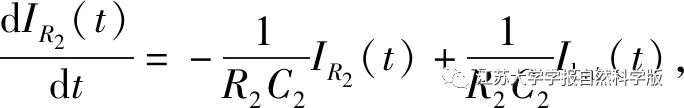
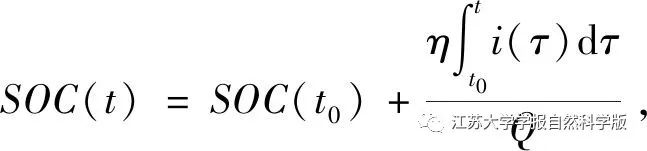

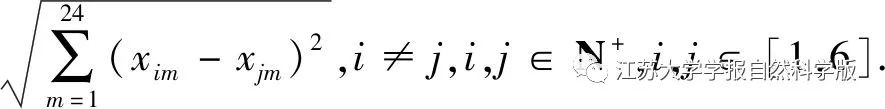

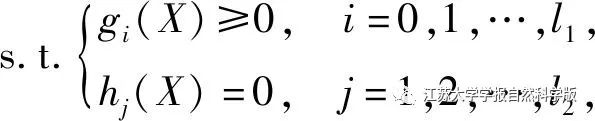
 Calculate the search direction
Calculate the search direction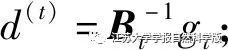 ③ Starting from the current point x(t), perform a one-dimensional search along d(t) to obtain the optimal step length λt, and update the current point x(t-1)=x(t) + λtd(t); ④ If |gt+1|<ε, stop the iteration; otherwise, proceed to step ⑤; ⑤ Calculate Δg=gt+1–gt, Δx=x(t+1)-x(t), update the approximate matrix
③ Starting from the current point x(t), perform a one-dimensional search along d(t) to obtain the optimal step length λt, and update the current point x(t-1)=x(t) + λtd(t); ④ If |gt+1|<ε, stop the iteration; otherwise, proceed to step ⑤; ⑤ Calculate Δg=gt+1–gt, Δx=x(t+1)-x(t), update the approximate matrix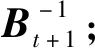 Set t=t+1, and return to step ②.
Set t=t+1, and return to step ②.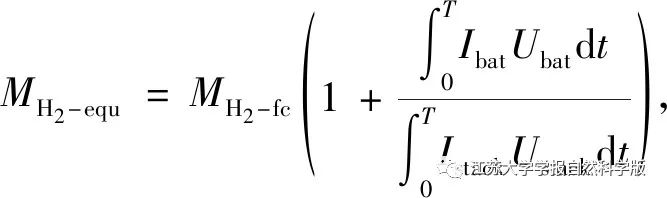
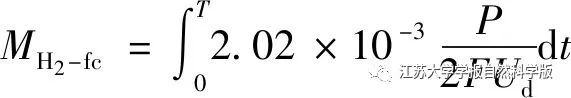
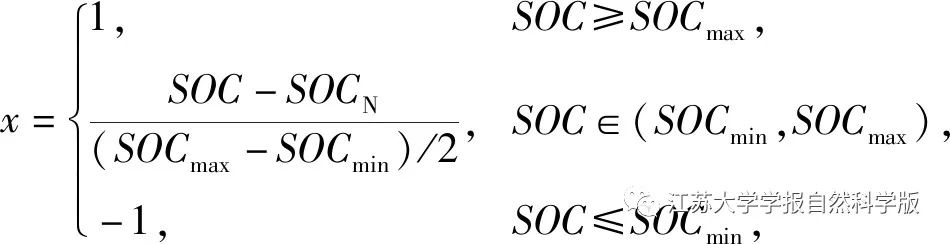
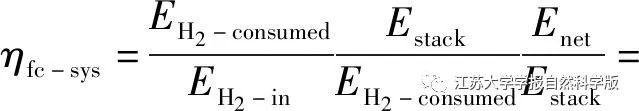 ηfuelηconvηelec=D(SOH,Pfc),
ηfuelηconvηelec=D(SOH,Pfc),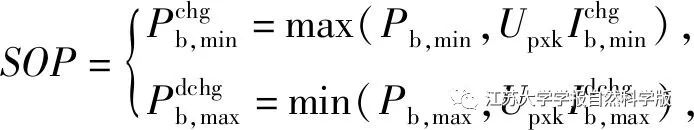
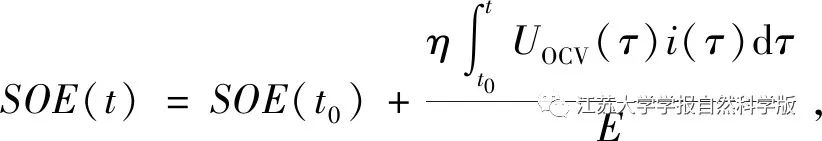
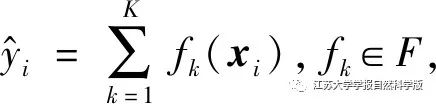
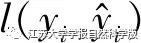
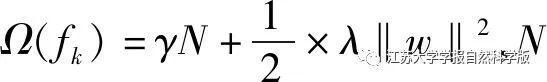 is the loss function;
is the loss function; 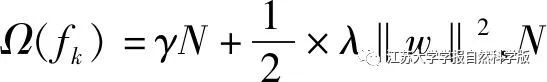 is the number of leaf nodes of the regression tree, γ is the number of leaf nodes, and λ is the regularization term penalty coefficient.
is the number of leaf nodes of the regression tree, γ is the number of leaf nodes, and λ is the regularization term penalty coefficient.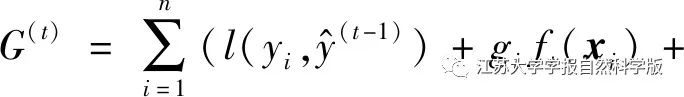
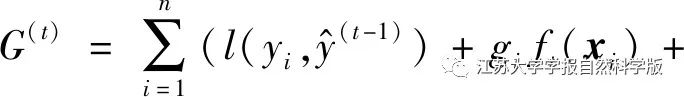
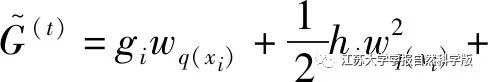
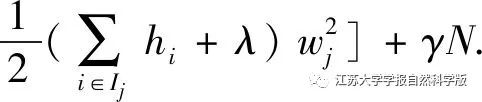
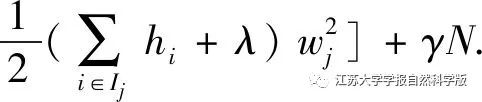
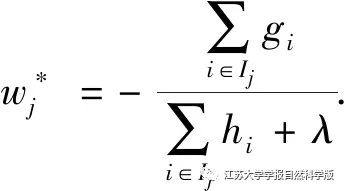
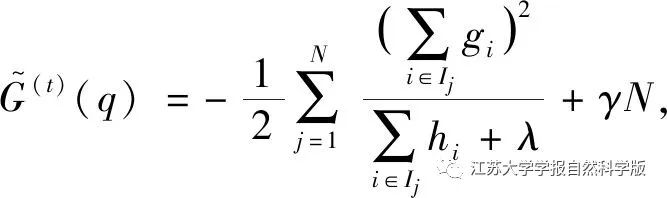


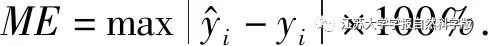
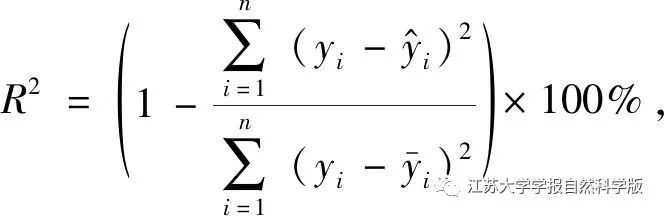
 is the average of the sample data.
is the average of the sample data.