Click the blue text above to follow us



Gift to Readers

👨💻Doing research involves a profound system of thought. Researchers need to be logical, diligent, and serious, but effort alone is not enough. Often, leveraging existing resources is more important than hard work. Additionally, one needs innovative and inspiring ideas. It is recommended that readers browse through the directory order to avoid suddenly falling into a dark maze without finding their way back. It may not reveal all the answers to your questions, but if it helps clarify the doubts rising in your mind, it could paint a beautiful sunset. If it brings you a spiritual storm, take the chance to brush off the dust from your previous complacency.
Perhaps, after the rain, the sky will be clearer…🔎🔎🔎



1 Overview

For basic first-order and second-order multi-agent control, basic Matlab simulation is provided.
For second-order multi-agents, two methods are provided.
MAS2-ode45 uses Matlab’s built-in ode45 method to solve differential equations, offering higher precision, corresponding to section 2.3.
2. MASsecond_order uses the Euler method to solve differential equations, with general precision, corresponding to section 2.2.
Python code is added for the first-order multi-agent case when each agent’s state is two-dimensional (multi-dimensional) and tends to consensus, corresponding to section 2.4.
1. Ode45 Method
Ode45 is a function in MATLAB used for solving ordinary differential equations (ODEs) numerically, particularly suitable for non-stiff ODEs. It employs a fourth-fifth order Runge-Kutta algorithm, where the fourth-order method provides candidate solutions and the fifth-order method controls the error, achieving adaptive step size (variable step) solutions.
Principle
The core of ode45 is the fourth-fifth order Runge-Kutta algorithm. This algorithm approximates the true solution by estimating several slopes and uses the fifth-order method to assess the error, thereby adjusting the step size to improve accuracy.
Syntax
The basic syntax of ode45 is as follows:
<span><span>[T,Y] = ode45(odefun,tspan,y0)</span></span> |
Where,<span><span>odefun</span></span> is the function handle describing the differential equation,<span><span>tspan</span></span> is the time interval for solving,<span><span>y0</span></span> is the initial condition.<span><span>T</span></span> returns the solved time points,<span><span>Y</span></span> returns the corresponding solution vector.
Example
Consider solving the first-order ordinary differential equation dy/dt = f(t,y), where f(t,y) = (y + 3t)/t^2, with the initial condition y(1) = -2, over the interval [1, 4]. The ode45 can be used as follows:
<span><span>odefun = @(t,y) (y + 3*t)/t^2;</span></span> |
<span><span>tspan = [1 4];</span></span> |
<span><span>y0 = -2;</span></span> |
<span><span>[t,y] = ode45(odefun,tspan,y0);</span></span> |
<span><span>plot(t,y);</span></span> |
<span><span>title('t^2y''=y+3t, y(1)=-2, 1<t<4');</span></span> |
<span><span>legend('t^2y''=y+3t');</span></span> |
<span><span>xlabel('t');</span></span> |
<span><span>ylabel('y');</span></span> |
2. Euler Method for Solving Differential Equations
The Euler method is a numerical method for solving differential equations, based on the principle of iteratively approaching the true solution.
Principle
The basic idea of the Euler method is to convert the differential equation into a difference equation and iteratively solve the difference equation to approximate the true solution. Specifically, for the first-order ordinary differential equation dy/dt = f(t,y), the iteration formula for the Euler method is:
<span><span>y_{k+1} = y_k + f(t_k, y_k) * Δt</span></span> |
Where, Δt is the step size, t_k is the time point at the k-th step, and y_k is the solution at the k-th step.
Error Analysis
The error in the Euler method mainly arises from the approximation of the integral. Since the Euler method uses the area of rectangles to approximate the integral, its truncation error is proportional to the square of the step size, i.e., O(Δt^2). This means that the precision of the Euler method is relatively low, but it remains an effective method for some simple differential equations and rough approximation needs.
Improved Methods
To improve accuracy, improved Euler methods (like Heun’s method, trapezoidal method, etc.) can be used. These methods enhance accuracy through more precise integral approximations, but correspondingly increase computational complexity.
3. Research on First-Order and Second-Order Multi-Agent Control
Multi-agent control is an emerging control method that exhibits unique advantages in cooperative control, distributed control, and fault-tolerant control. Below is a brief overview of the research on first-order and second-order multi-agent control.
First-Order Multi-Agent Control
For first-order multi-agent systems, consensus protocols can be used to achieve cooperative control. Consensus protocols are based on neighbor information exchange and adjust each agent’s control input to make all agents’ states converge.
Second-Order Multi-Agent Control
For second-order multi-agent systems (such as drone systems with position and velocity states), a leader-based second-order consensus protocol can be employed for cooperative control. This protocol not only considers neighbor information exchange but also incorporates leader information to guide the entire system’s motion.
Simulation and Analysis
To verify the effectiveness of the above algorithms, simulations can be conducted in the MATLAB environment. Through simulations, the cooperative movement process of multi-agent systems can be visually observed, and the performance metrics of the algorithms (such as convergence speed, accuracy, etc.) can be analyzed.
Applications and Outlook
Multi-agent control methods have broad application prospects in areas such as drone control, robot collaboration, and intelligent transportation. Future research can further focus on more complex multi-agent systems (such as nonlinear systems, time-varying systems, etc.) and the feasibility of multi-agent control in practical applications.
In summary, the ode45 method, the Euler method for solving differential equations, and the research on first-order and second-order multi-agent control are important topics in control theory and engineering. In-depth research on these methods and techniques can provide strong theoretical support and technical guarantees for practical engineering applications.


2 Running Results


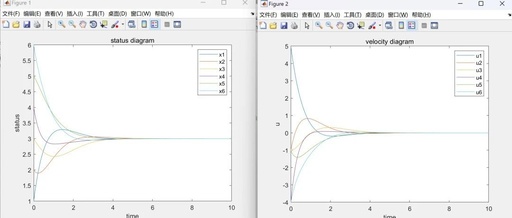
2.1 MASfirst-order
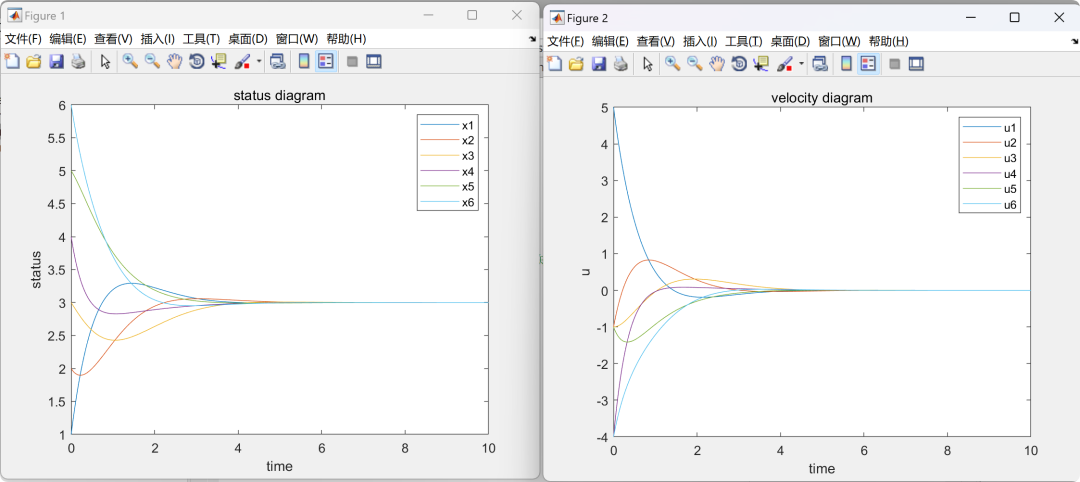

2.2 MASsecond-order
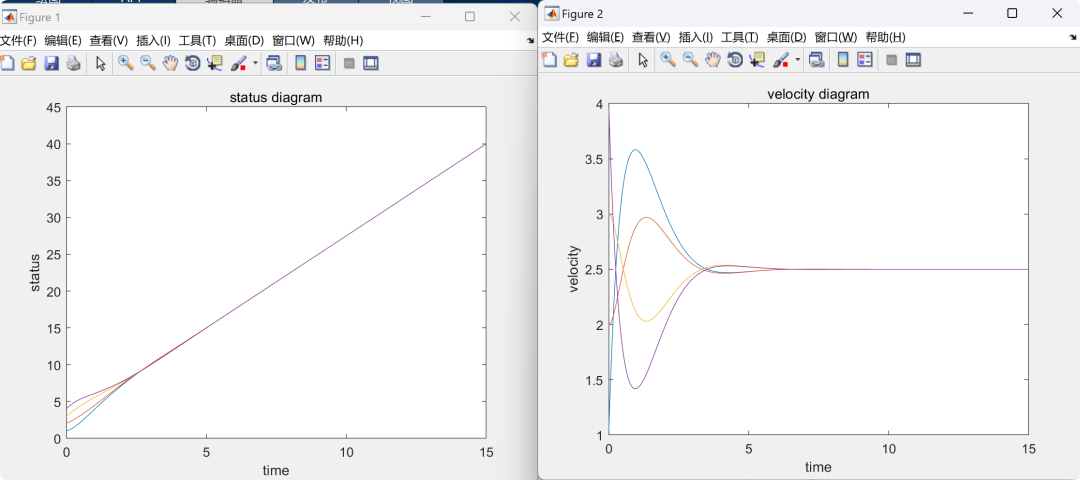
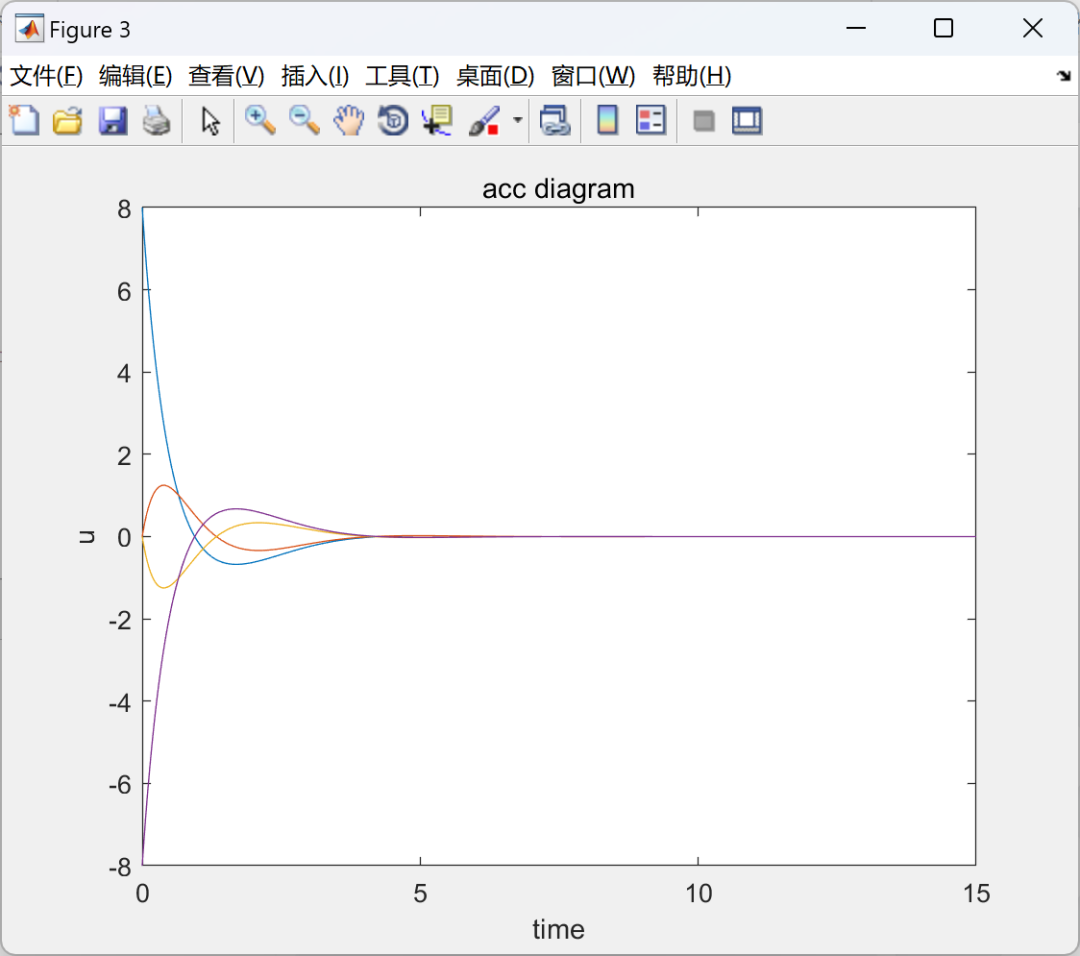

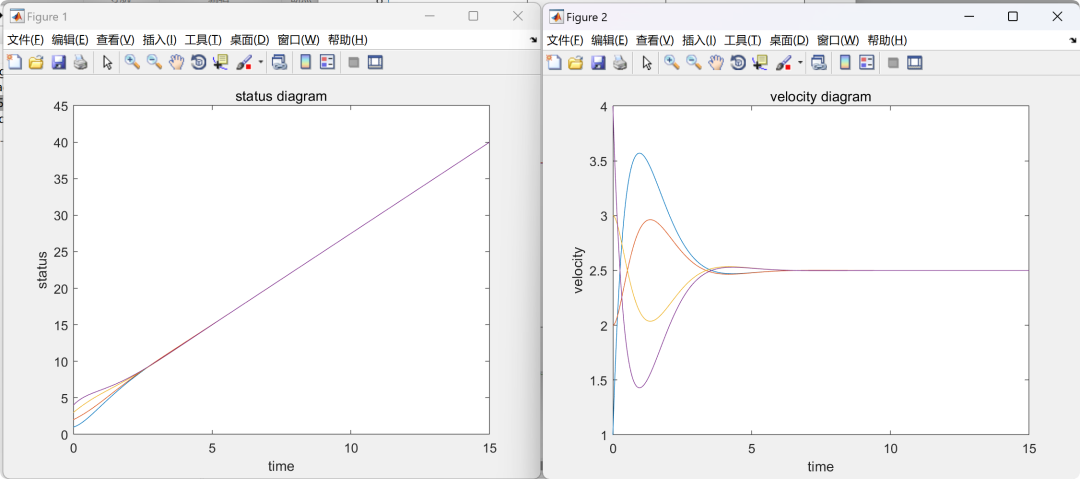
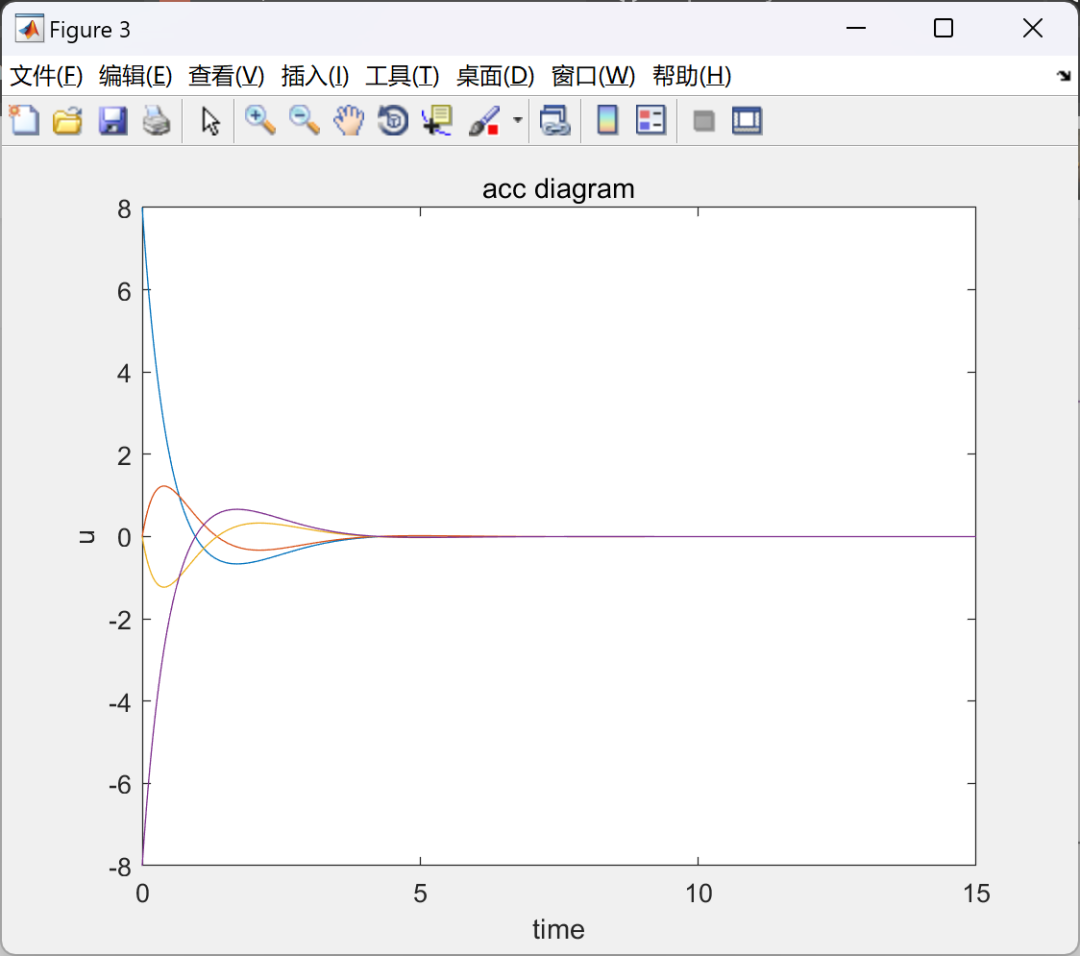
2.3 MAS2-ode45

2.4 first_order_agent (Python Code)
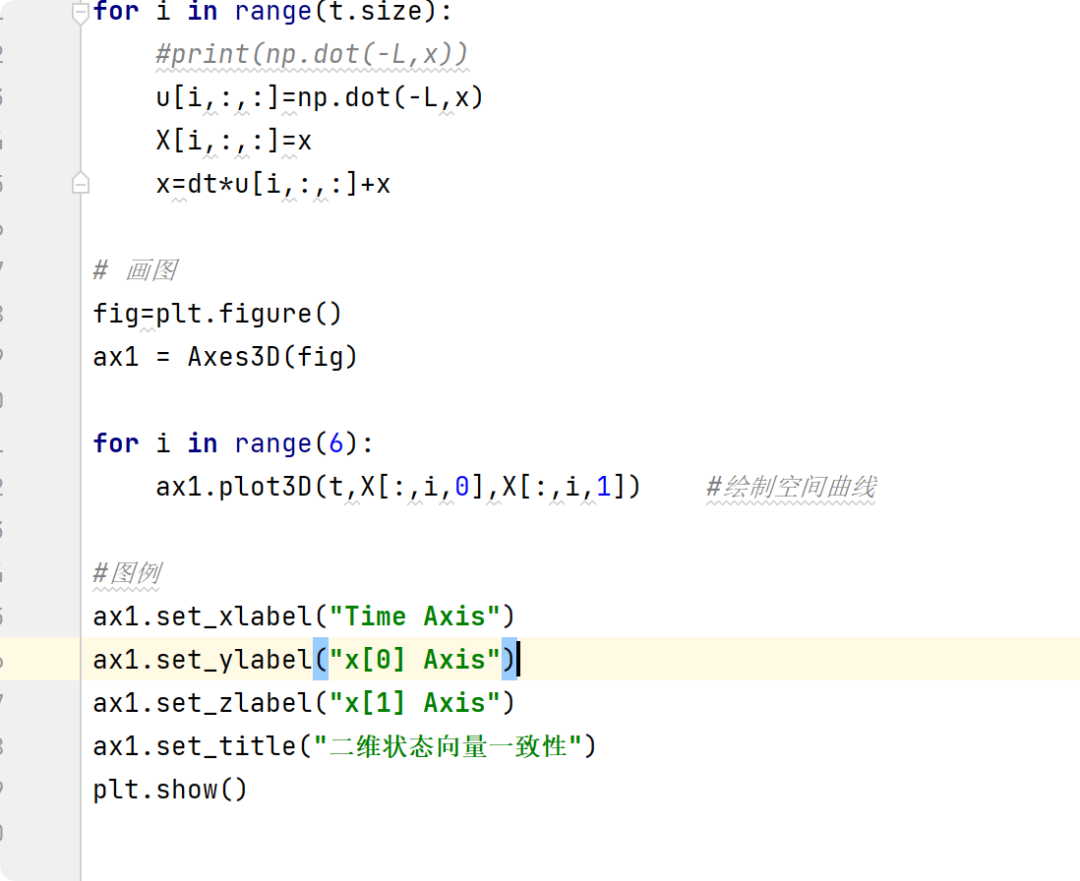
% Part of the code:
A=[0 1 0 1;1 0 1 0;0 1 0 1;1 0 1 0];% Adjacency matrix
D=diag(sum(A,2));% Construct D matrix using Laplacian with row sums equal to 0
L=D-A;% Calculate the Laplacian matrix using the definition
u0=-(L*X0+gamma*L*V0);% Initial value of u0
options = odeset('MaxStep', 1e-2, 'RelTol',1e-2,'AbsTol',1e-4);
[t,y] = ode45(@odefun,[0 15],[X0;V0;u0],options);
X=y(:,1:4);
V=y(:,5:8);
u=y(:,9:12);
% Plotting section
figure(1);
plot(t,X)
title('status diagram');


3 References

Some content in this article is cited from the internet, with sources noted or referenced as literature. If there are any discrepancies, please feel free to contact for deletion. (The content of the article is for reference only, specific effects are subject to the running results.)

[1] Pan Huan. Research on Second-Order Multi-Agent Consensus Algorithms [D]. Central South University [2025-01-18].
[2] Gao Yanping, Jiang Tongqiang, Wang Wen, et al. Consensus Analysis of Second-Order Multi-Agent Systems [J]. Complex Systems and Complexity Science, 2014, 11(4):5.
[3] Cheng Yongli. Research on Tracking Control of Second-Order Multi-Agent Systems [D]. Tianjin University [2025-01-18].



4 Matlab Code, Python Code

For more resources on MATLAB|Simulink|Python, and more fan benefits.