Machine Learning 9.4D XG Algorithm 4: Second Order Approximation

XGBoost utilizes a second technique which is second-order optimization, expanding the loss function l(x,y) using a Taylor series expansion.

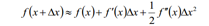
To approximate it to the second order. This is relatively unique in the XGBoost algorithm, differing from the approach of optimizing using gradient descent in GBT, and also different from Adaboost which increases the weights of misclassified samples at each iteration.

We express the residual part of the loss function in the XGBoost algorithm using a second-order Taylor expansion:

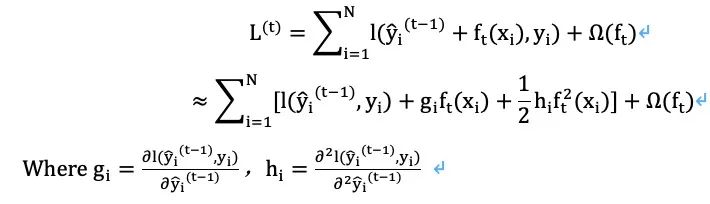
Since our optimization goal is to find the optimal tree f_t(x), during this (tth) optimization process, the first term in Σ, l(y_i^^(t-1), y_i), is independent of this optimization and can be treated as a constant. To simplify calculations, we remove the constant term, resulting in the following objective function L~^(t). Optimizing this objective function L~^(t) is equivalent to optimizing L^(t) to obtain f(t), differing only by a constant term in the loss function itself.

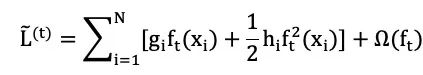
Since we are using such a CART tree, we define I_j as the space of leaf node j. For any sample falling into I_j, the final output is w_j, where j=1,2,…T. Substituting into the above objective function L~^(t) gives us

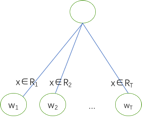
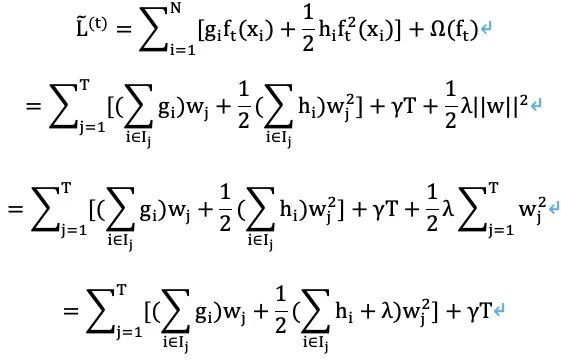
At this point, our goal is to find the score for each tree’s leaf node j. After determining w_j, we can sum the w_j values from each tree to obtain the final predicted score.

To obtain the optimal value of w_j, which minimizes our objective function, we take the partial derivative of the above expression with respect to w_j and set it to 0, yielding the value of w_j* as:

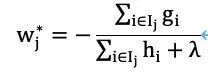
Based on this, we define the sum of the first and second derivatives at leaf node j as G_j and H_j, respectively, leading to:

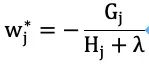
Substituting into the loss function L~^(t) gives us

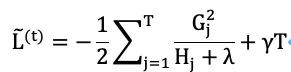
This can serve as a score to evaluate model quality; the higher the score, the worse the model’s performance.