The 2024 Nobel Prize in Physics is awarded for “fundamental discoveries and inventions in machine learning through artificial neural networks.” Artificial neural networks can be said to be the machine learning revolution triggered by statistical physics (Science for AI). The Nobel Prize in Chemistry is awarded for research related to protein design and structure prediction, showcasing the significant role of artificial intelligence in driving scientific innovation (AI for Science). This bidirectional interaction between artificial intelligence and science has ushered in a new era of AI+Science, accelerating the understanding of complex systems.
Is it surprising that the 2024 Nobel Prize in Physics is awarded for machine learning? What is the connection between machine learning and statistical physics? How do the developments in artificial intelligence and science empower each other? What insights can statistical physics and complex systems provide for artificial intelligence research? Will AI surpass human understanding to discover new physics? What will be the next Nobel Prize-worthy scientific research? To address these questions, we invited three intelligent scientists: Professor You Yizhuang from the University of California, San Diego, Professor Zhang Jiang from the School of Systems Science at Beijing Normal University and founder of the Intelligent Club, and Assistant Professor Tang Qianyuan (Fu Wocheng) from Hong Kong Baptist University, to delve into the interpretation of the 2024 Nobel Prize. This article is a transcription of the discussion, shared with our readers.
Research Fields: Statistical Physics, Complex Systems, Quantum Mechanics, Artificial Intelligence, Neural Networks, Renormalization Group
Yizhuang You, Jiang Zhang, Qianyuan Tang | Speakers
Xinyi Zhu | Organizer
Jin Liang | Editor
Table of Contents
-
Is it surprising that the 2024 Nobel Prize in Physics is awarded for machine learning?
-
What are the main contributions of John Hopfield and Geoffrey Hinton?
-
What is the connection between machine learning and statistical physics?
-
How do the developments in AI and science empower each other?
-
What insights can statistical physics and complex systems provide?
-
Will AI surpass human understanding to discover new physics?
-
What will be the next Nobel Prize-worthy scientific research?
– 1 –
Is it surprising that the 2024 Nobel Prize in Physics is awarded for machine learning?
Is it surprising?
Q: The 2024 Nobel Prize in Physics awarded research related to machine learning has sparked widespread attention and discussion among the public and the physics community. Many find it hard to understand why such an important physics award is given to research in computer science. At the same time, computer scientists are puzzled as to why physicists are venturing into their field. In this context, what are your thoughts on this Nobel Prize in Physics?
Zhang Jiang: I am quite surprised. Generally speaking, the Nobel Prize in Physics is usually awarded to research closely related to material science and physical systems, except for the 2021 award which was given to scientists studying complex physical systems, including atmospheric systems. According to our usual understanding, artificial intelligence is a branch of computer science, seemingly not closely related to physics, yet this year’s Nobel Prize in Physics was awarded to research related to artificial intelligence, which I find very surprising. Moreover, while the Hopfield network and some early research by Hinton are groundbreaking in the field of artificial intelligence, from the perspective of modern AI, these models seem a bit outdated; we have basically surpassed these early models. Therefore, I believe this award in physics is indeed shocking.
You Yizhuang: Everyone is surprised by this year’s Nobel Prize in Physics results. I noticed many colleagues chose to remain silent about it, preferring not to discuss it. In the United States, AI is increasingly being researched in physics departments, and people are gradually realizing that AI has a deep physical foundation and is closely related to physics. I feel that the professors around me seem to be more accepting of this.
Of course, on the whole, people still find it quite surprising, as AI is not one of the major fields of traditional physics. Traditionally, the Nobel Prize in Physics is often awarded in areas like quantum physics, astrophysics and cosmology, high-energy physics, condensed matter physics, and atomic and molecular physics. Before this year’s Nobel Prize announcement, people speculated in this order: which field should be next, given that these fields have taken turns in recent years. However, most of these speculations fell flat. This may indicate that from the perspective of the Nobel Prize committee, issues such as artificial intelligence, complex systems, and even the origins of intelligence or consciousness may gradually become new areas of research in physics. Physics itself should also keep pace with the times.
Therefore, although the awarded content seems, as Professor Zhang Jiang mentioned, somewhat lagging compared to current deep learning technologies, from the perspective of the development of physics paradigms and innovation across the discipline, the awarding of this prize is very timely.
Tang Qianyuan: I would like to add that although this year’s Nobel Prize in Physics results were unexpected, a popular post circulating online recently revealed an interesting phenomenon. Someone found that a textbook had already labeled Hopfield as a Nobel Prize winner in Physics during its introduction, which was actually a prophecy, as he had not yet won the award at that time. This indicates that despite misunderstandings, many people already believed that his achievements were worthy of Nobel recognition. This error may have been due to the author mistakenly thinking he was already a Nobel laureate while writing. Therefore, it shows that the physics community highly recognizes Hopfield’s contributions; he even received the Boltzmann Award at the Statistical Physics Conference in 2022, which is the highest honor in statistical physics, indicating that the physics community holds Hopfield’s contributions in very high regard. Hinton’s award, on the other hand, was relatively unexpected.
– 2 –
What are the main contributions of John Hopfield and Geoffrey Hinton?
Tang Qianyuan: Let’s start with Hopfield; I can introduce some of his work beyond the Hopfield network. In fact, his father was also a physicist, and he has always been involved in physics, initially working in the field of condensed matter. Later, starting in the 1970s, he began to shift towards biophysics. Initially, he studied a proofreading mechanism in biochemical reactions, as many biochemical reactions involve randomness that can be corrected through certain non-equilibrium mechanisms. Before the establishment of non-equilibrium physical systems, Hopfield had already proposed this mechanism. He then began studying neural networks, which led to the development of the Hopfield network. After this research, he did a lot more work, such as on the coding mechanisms for olfactory problems and more theoretical studies related to neural networks. In recent years, he has continued to conduct related research and remains an active scholar. Regarding the Hopfield network, I would like to hear from Professor Zhang Jiang about the earliest energy-based models to give everyone a brief introduction.
Zhang Jiang: About 20 years ago, when the Intelligent Club was just established, I attended a summer school jointly held by the Santa Fe Institute and the Institute of Theoretical Physics at the Chinese Academy of Sciences. After learning a lot about statistical physics, I began to enter this field. I was particularly impressed by the Ising model, which has a popular science introduction in encyclopedias; we can understand it as a scenario where villagers vote, where each villager may be influenced by their neighbors, forming an interactive system of mutual influence.
“Ising Model” Intelligent Encyclopedia: What is the Ising Model | Intelligent Encyclopedia
https://wiki.swarma.org/index.php/Ising_Model
In this system, the most interesting aspect is the competition between order and disorder. The so-called order means that each villager must obey the majority to some extent, influenced by their neighbors, while disorder indicates that there is some randomness in each villager’s voting choice. In this physical system, the Ising model was originally used to model the phase transition behavior of ferromagnetic and paramagnetic materials (i.e., magnets): when the temperature rises to a certain point, it becomes very disordered; at low temperatures, it exhibits corresponding magnetic properties, and all spins behave consistently. Interestingly, there is a critical point, and near this critical point, the entire system becomes very complex, exhibiting fractal, self-similar structures and other interesting phenomena.
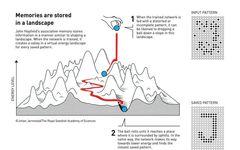
So what is the relationship between this and the Hopfield network? In fact, the Hopfield network is an extension of the Ising model. The Ising model is a lattice system, which is transformed into a fully connected network where the strength of connections can take random values, thus becoming a very complex network. At the same time, we can use a learning mechanism to allow the weights of the network to change, so that the minimum energy points correspond to the patterns we need to remember. Therefore, when the Hopfield network was first created, it was originally used for associative memory. For example, if we provide it with some data containing patterns like handwritten digits such as 1234, it will gradually converge, and its minimum energy will correspond to these patterns. Conversely, when running, if we provide it with a stimulus that resembles a certain handwritten digit, it will gradually converge to that attractor, thereby recovering the pattern stored in memory; this is the earliest Hopfield model.
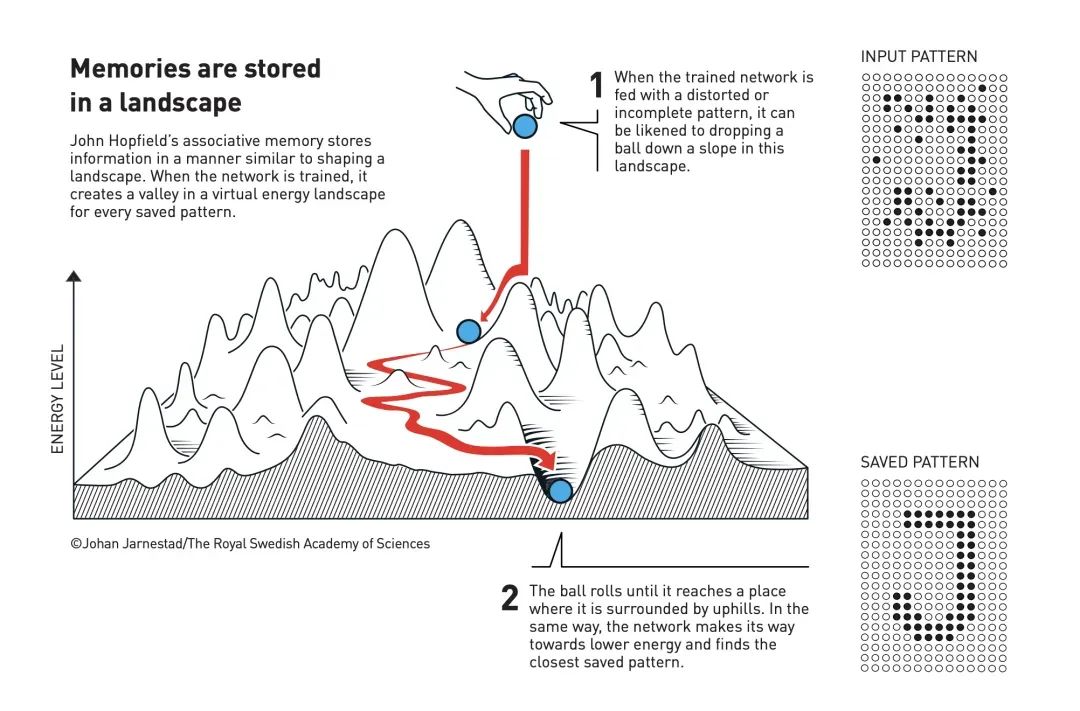 Figure 1. The Hopfield network can store and reconstruct patterns in data.
You Yizhuang: I believe that both works awarded this year’s Nobel Prize in Physics are closely related to statistical physics. The Hopfield model proposed by Hopfield is one of the earliest energy-based generative models, which actually utilizes a fundamental principle from statistical physics—the Boltzmann distribution. In fact, what we now refer to as energy-based generative models is the most basic method of equilibrium statistical physics. In the early days, physicists wanted to understand how the collective behaviors of many individuals interacted, which was the main goal of statistical physics. The term “statistical” in statistical physics refers to the statistics of individual behaviors.
For example, I was very interested in simulating the interactions between multiple particles when I was a child and would write computer models to simulate them. At that time, I had an idea that if I could understand the motion of all particles, I would be able to understand the macroscopic behavior. But later I found out that I was wrong; understanding the motion of individual particles does not help you understand macroscopic behavior. On the contrary, macroscopic behavior often only depends on a few quantities, such as the total energy of the system. Statistical physicists later discovered that the probability distribution in a many-body system only depends on the energy function of that many-body system; people can write down the expression corresponding to the probability distribution and energy function, and basically, the energy function is proportional to the logarithm of the probability distribution. Based on this principle, we can use the energy function to simulate the distributions of many different many-body systems. These many-body systems naturally include magnetic systems. In studying magnetic systems, physicists found that magnetic systems at low temperatures exhibit many different patterns, such as ferromagnetic and antiferromagnetic states. Many strange spin glass states appear. After some research, it was found that these states are related to the interactions between spins and how energy is distributed. This forms the macroscopic phenomenon we observe—there is a hidden energy behind the formation of a certain pattern.
However, I believe that Hopfield’s work represents a paradigm shift based on equilibrium statistical physics. Why do I say this? Previously, equilibrium statistical physics asked: given an energy function and the interactions of the system, what behaviors does it exhibit at high and low temperatures? People wanted to solve the behaviors of this system. But Hopfield said: No, you can change the problem, you can modify your energy function, you can modify the interaction patterns between these spins . By modifying the interaction patterns, you expect to form a specific pattern that you want to achieve. This actually transforms statistical mechanics from a discipline that answers questions into a learning process that seeks to find the generative mechanism behind a certain pattern through observation of spin patterns. He thought to reverse the question, allowing one to observe spin patterns and then modify the interaction model to best stabilize the spin patterns. This model can naturally utilize the power of statistical physics to reproduce the corresponding structure at low temperatures. Moreover, when the structure is disrupted, lowering the temperature again can correct this disruption or error.
These works actually have significant applications in modern information processing. We all know that errors can occur during communication processes, and modern quantum computing can also generate errors during calculations, and these errors need to be corrected. In fact, methods like Hopfield’s that use energy models to establish some underlying mechanisms and then correct errors by cooling down are one of the most natural error correction mechanisms. I remember that early computers used disk storage. The reason disks can store information for a long time is that they have this ferromagnetic error correction mechanism. Although disks are in a complex environment and may occasionally have some spin flips, they can still rely on many-body interactions to correct these errors.
Therefore, I think the remarkable aspects of this work are reflected in two aspects. First, it changes our view of statistical physics; it is no longer simply a group of physicists seeking to solve the conditions of a mathematical model under low-temperature environments, but rather thinking about how to build a new model from real data. Secondly, it also tells us how to use physics to help us correct errors, how physics is related to information, and how it relates to coding. This is why I believe it is very deserving of this Nobel Prize, and indeed, this Nobel Prize is very relevant to physics.
Zhang Jiang: I would like to add the value and significance of Hinton’s work for neural network research and its relationship with the Hopfield network. In fact, when I first came into contact with neural networks, I was completely unaware of their connection to statistical physics. Neural networks seem to be simple input receivers, where each neuron receives input signals, and when enough input is received, the neuron may be activated and continue to propagate signals. Through the gradient backpropagation method, we can train the network to learn. During my undergraduate studies, we worked on a project using feedforward neural networks to learn patterns in data and make predictions. But it wasn’t until I attended a summer school and came into contact with the Ising model that I had a sudden realization and recognized that neural networks could correspond completely to the Ising model and spins.
We can view each neuron as a spin in the Ising model (spin), where each spin has two states: up or down, corresponding to the activation and non-activation states of the neuron. In the Ising model, the state of each spin is influenced by its neighbors and its own randomness. For neural networks, other neurons also influence its state, so they also determine whether to activate through interactions. Additionally, the activation function itself maps randomness into the S-shaped activation function curve, thus establishing the relationship between the two. I believe that the earliest clear establishment of this relationship, and the ability for neural networks to operate in a statistical physics manner, is closely linked to Hinton’s research work. One major improvement he made to neural networks was to divide the network into two layers: one is the visible layer, equivalent to the input layer, used to receive data; the other is the hidden layer, which serves to compress and represent data. In today’s deep learning, this kind of representation learning—obtaining compressed representations of data—is very important and is the basis for how our brains process complex information. Therefore, I believe Hinton’s research work is remarkable as he completely integrated the concepts of statistical physics into the field of neural networks.
Tang Qianyuan: Hopfield’s contribution also reflects the very fundamental concept of “more is different.” Anderson regarded Hopfield as a hidden collaborator who had not co-authored papers with him. In traditional neuroscience, it was believed that memories in the brain are stored in specific areas, but Hopfield proposed a completely new perspective: memories are not stored in any one place in the brain, but rather are stored in all places in the brain. All neurons work together to form memories, which may be how the brain performs memory and other functions. Moreover, this mechanism has its corresponding neuroscience background, known as the “Hebbian learning rule,” which simply states that “during learning, if two neurons often fire together, they are more likely to connect,” that is, “Fire together wire together.” This mechanism is what Professor You Yizhuang just mentioned, how to encode a pattern to be remembered in neurons. Hopfield concretized this concept through a physical model, which is an important contribution of his.
In addition, Hopfield has another lesser-known contribution. As Professor Zhang Jiang also mentioned, criticality is a very key feature in magnetic systems. After the concept of self-organized criticality was proposed by Professor Tang Chao and others, Hopfield also became interested in critical phenomena in the brain early on and wrote papers using seismic models to illustrate the possible critical mechanisms in the brain. Therefore, Hopfield can also be regarded as a pioneer of the brain’s criticality hypothesis. (See: “How Nature Works”: A Science on Self-Organized Criticality | Preface recommended by Academician Tang Chao”)
Regarding Hinton’s contributions, the Boltzmann machine proposed by Hinton can be seen as a generalization of the Hopfield model. The Boltzmann machine itself is fully connected, but due to the excessive number of connections that need to be processed, it is not very practical. It was later transformed into a restricted Boltzmann machine, distinguishing between hidden and input layers. Although Hinton was not the original inventor of the restricted Boltzmann machine, his contributions cannot be ignored; in fact, he rediscovered this model and proposed a training method called contrast divergence, making the Boltzmann machine truly usable. Contrast divergence is a complex iterative process, but some of Hinton’s work made it feasible. Thus, I look forward to Professor You Yizhuang further discussing Hinton’s contributions to contrast divergence and sampling.
You Yizhuang: Hinton’s work is actually an advancement of the Hopfield model; he elevated the Hopfield model to new heights. The core goal of this generative model is to learn an energy function that represents the probability density distribution of samples. All generative models need to be trained based on samples.
But how to train the Boltzmann machine becomes a problem. Hinton thought of some very clever methods for training; his basic idea is this: if we use some energy function as a model to generate a probability density distribution, and the samples themselves also have their own probability density distribution. In principle, we hope that these two probability density distributions are as close as possible, that is, to make the model’s distribution as close as possible to the sample’s distribution. We need to minimize a quantity called KL divergence—representing the relative difference between the two distributions. After some research, he found that relative entropy can basically be expressed as: the difference between two free energies.
This is actually a very interesting point. Imagine that if we let the model run with its eyes closed, it will produce a free energy of a statistical mechanical system, which represents the system’s energy in some average sense. When there are sample data in the visible layer, we call this “claimed free energy,” and when data is forcibly loaded into the visible layer, the model will also have a free energy. The difference between these two free energies is exactly what the KL divergence represents as the loss function.
This points us in a training direction, as if the relationship between closing and opening our eyes. During the training process, you can first let the model close its eyes and imagine. Suppose I have a bunch of spins, some of which belong to the visible layer, and they need to be consistent with the data; the others belong to the hidden layer, which is not important for them. During the closed-eye phase, we observe how strong the correlations are between the visible layer spins, which is what the model imagines or “dreams” during its process. Then, when data is present, the model will again observe the visible layer data, studying how strong the correlations are between the visible and hidden layers when the visible layer data is fixed and the thermodynamic system reaches equilibrium. For example, in a restricted Boltzmann machine, we only need to care about the correlations between the visible and hidden layers. Therefore, we only need to compare the strengths of correlations in the presence and absence of data to determine whether the connection between the visible and hidden layers should be strengthened or weakened. If the correlations are weaker when data arrives, and stronger in the absence of data, it indicates that the system’s imagination does not match reality, thus the coupling strength between them should be reduced to achieve this. This is the basic idea of contrast divergence.
It is similar to our usual learning process, where we have both textbook learning and closed-book thinking. As Confucius said, “Learning without thinking is labor lost; thinking without learning is perilous,” meaning learning and thinking should be combined. I believe the idea of contrast divergence very well embodies the combination of learning and thinking processes. When data comes in, you need to learn to reach a certain balance, and you also need to think, then compare the differences between learning with open and closed eyes to adjust your neural network weights.
Of course, this process involves steps of thermal equilibrium. When data is input, we need to achieve thermal equilibrium for the entire system based on the data, which means going through repeated sampling iterations to bring the spin system to equilibrium. In the closed-eye thinking phase, multiple sampling iterations are also necessary. This involves considerations of computational complexity. Early algorithms were not very successful, partly because using Monte Carlo sampling methods on spin models required substantial computational resources. Hinton made a very important observation: in fact, you do not need to let the two systems reach thermal equilibrium. Although mathematically, you should compare the correlation strengths between equilibrium states, we can actually already see the differences in correlations between the closed and open eye states—i.e., in the presence and absence of data—this can already provide some learning signals. Hinton also proved that even if you follow such an incorrectly complete signal, the minimum point of the loss function will be the same as the original minimum point. This allows us to sample and learn more efficiently. These ideas transitioning from equilibrium to non-equilibrium physics are very interesting thoughts in statistical mechanics. I believe these are all valuable for us to think about and learn from.
Zhang Jiang: Hinton has played two key roles as a savior in the history of neural network research. The first time was around the 1980s. Before that, since the inception of artificial intelligence in 1956, the mainstream was traditional AI focused on search and logical reasoning. Although the concept of neural networks can be traced back to the mathematical model proposed by Warren McCullough and Walter Pitts in 1943, Minsky and Papert proved in their book “Perceptrons” that single-layer perceptron models could not solve simple XOR and other linearly inseparable problems, which nearly killed the neural network discipline. During that period, researchers feared their papers would not be published, and the neural network discipline was on the brink of extinction. However, it was Hinton who persisted in neural network research and successfully applied the backpropagation algorithm to train multi-layer neural networks, marking the first time he saved the neural network discipline.
The second rescue occurred during the early stages of deep learning. At that time, although neural networks were performing well in many learning tasks, their limited depth restricted the problems they could solve. Therefore, many people were not optimistic about neural networks, and there were many competing algorithms. Hinton demonstrated the potential of deep neural networks by making restricted Boltzmann machines very deep, and according to my recollection, he may have been the first to use the term “deep neural network” in a 2006 paper. This made people realize that it was not that neural networks were ineffective, but that we had not made them deep enough. When we deepened them, they really worked well and achieved excellent results. Initially, they made significant breakthroughs in speech recognition and image recognition, allowing more people to see that we could use deep learning to enable artificial intelligence to learn entirely through deep means and achieve very good results.
Figure 1. The Hopfield network can store and reconstruct patterns in data.
You Yizhuang: I believe that both works awarded this year’s Nobel Prize in Physics are closely related to statistical physics. The Hopfield model proposed by Hopfield is one of the earliest energy-based generative models, which actually utilizes a fundamental principle from statistical physics—the Boltzmann distribution. In fact, what we now refer to as energy-based generative models is the most basic method of equilibrium statistical physics. In the early days, physicists wanted to understand how the collective behaviors of many individuals interacted, which was the main goal of statistical physics. The term “statistical” in statistical physics refers to the statistics of individual behaviors.
For example, I was very interested in simulating the interactions between multiple particles when I was a child and would write computer models to simulate them. At that time, I had an idea that if I could understand the motion of all particles, I would be able to understand the macroscopic behavior. But later I found out that I was wrong; understanding the motion of individual particles does not help you understand macroscopic behavior. On the contrary, macroscopic behavior often only depends on a few quantities, such as the total energy of the system. Statistical physicists later discovered that the probability distribution in a many-body system only depends on the energy function of that many-body system; people can write down the expression corresponding to the probability distribution and energy function, and basically, the energy function is proportional to the logarithm of the probability distribution. Based on this principle, we can use the energy function to simulate the distributions of many different many-body systems. These many-body systems naturally include magnetic systems. In studying magnetic systems, physicists found that magnetic systems at low temperatures exhibit many different patterns, such as ferromagnetic and antiferromagnetic states. Many strange spin glass states appear. After some research, it was found that these states are related to the interactions between spins and how energy is distributed. This forms the macroscopic phenomenon we observe—there is a hidden energy behind the formation of a certain pattern.
However, I believe that Hopfield’s work represents a paradigm shift based on equilibrium statistical physics. Why do I say this? Previously, equilibrium statistical physics asked: given an energy function and the interactions of the system, what behaviors does it exhibit at high and low temperatures? People wanted to solve the behaviors of this system. But Hopfield said: No, you can change the problem, you can modify your energy function, you can modify the interaction patterns between these spins . By modifying the interaction patterns, you expect to form a specific pattern that you want to achieve. This actually transforms statistical mechanics from a discipline that answers questions into a learning process that seeks to find the generative mechanism behind a certain pattern through observation of spin patterns. He thought to reverse the question, allowing one to observe spin patterns and then modify the interaction model to best stabilize the spin patterns. This model can naturally utilize the power of statistical physics to reproduce the corresponding structure at low temperatures. Moreover, when the structure is disrupted, lowering the temperature again can correct this disruption or error.
These works actually have significant applications in modern information processing. We all know that errors can occur during communication processes, and modern quantum computing can also generate errors during calculations, and these errors need to be corrected. In fact, methods like Hopfield’s that use energy models to establish some underlying mechanisms and then correct errors by cooling down are one of the most natural error correction mechanisms. I remember that early computers used disk storage. The reason disks can store information for a long time is that they have this ferromagnetic error correction mechanism. Although disks are in a complex environment and may occasionally have some spin flips, they can still rely on many-body interactions to correct these errors.
Therefore, I think the remarkable aspects of this work are reflected in two aspects. First, it changes our view of statistical physics; it is no longer simply a group of physicists seeking to solve the conditions of a mathematical model under low-temperature environments, but rather thinking about how to build a new model from real data. Secondly, it also tells us how to use physics to help us correct errors, how physics is related to information, and how it relates to coding. This is why I believe it is very deserving of this Nobel Prize, and indeed, this Nobel Prize is very relevant to physics.
Zhang Jiang: I would like to add the value and significance of Hinton’s work for neural network research and its relationship with the Hopfield network. In fact, when I first came into contact with neural networks, I was completely unaware of their connection to statistical physics. Neural networks seem to be simple input receivers, where each neuron receives input signals, and when enough input is received, the neuron may be activated and continue to propagate signals. Through the gradient backpropagation method, we can train the network to learn. During my undergraduate studies, we worked on a project using feedforward neural networks to learn patterns in data and make predictions. But it wasn’t until I attended a summer school and came into contact with the Ising model that I had a sudden realization and recognized that neural networks could correspond completely to the Ising model and spins.
We can view each neuron as a spin in the Ising model (spin), where each spin has two states: up or down, corresponding to the activation and non-activation states of the neuron. In the Ising model, the state of each spin is influenced by its neighbors and its own randomness. For neural networks, other neurons also influence its state, so they also determine whether to activate through interactions. Additionally, the activation function itself maps randomness into the S-shaped activation function curve, thus establishing the relationship between the two. I believe that the earliest clear establishment of this relationship, and the ability for neural networks to operate in a statistical physics manner, is closely linked to Hinton’s research work. One major improvement he made to neural networks was to divide the network into two layers: one is the visible layer, equivalent to the input layer, used to receive data; the other is the hidden layer, which serves to compress and represent data. In today’s deep learning, this kind of representation learning—obtaining compressed representations of data—is very important and is the basis for how our brains process complex information. Therefore, I believe Hinton’s research work is remarkable as he completely integrated the concepts of statistical physics into the field of neural networks.
Tang Qianyuan: Hopfield’s contribution also reflects the very fundamental concept of “more is different.” Anderson regarded Hopfield as a hidden collaborator who had not co-authored papers with him. In traditional neuroscience, it was believed that memories in the brain are stored in specific areas, but Hopfield proposed a completely new perspective: memories are not stored in any one place in the brain, but rather are stored in all places in the brain. All neurons work together to form memories, which may be how the brain performs memory and other functions. Moreover, this mechanism has its corresponding neuroscience background, known as the “Hebbian learning rule,” which simply states that “during learning, if two neurons often fire together, they are more likely to connect,” that is, “Fire together wire together.” This mechanism is what Professor You Yizhuang just mentioned, how to encode a pattern to be remembered in neurons. Hopfield concretized this concept through a physical model, which is an important contribution of his.
In addition, Hopfield has another lesser-known contribution. As Professor Zhang Jiang also mentioned, criticality is a very key feature in magnetic systems. After the concept of self-organized criticality was proposed by Professor Tang Chao and others, Hopfield also became interested in critical phenomena in the brain early on and wrote papers using seismic models to illustrate the possible critical mechanisms in the brain. Therefore, Hopfield can also be regarded as a pioneer of the brain’s criticality hypothesis. (See: “How Nature Works”: A Science on Self-Organized Criticality | Preface recommended by Academician Tang Chao”)
Regarding Hinton’s contributions, the Boltzmann machine proposed by Hinton can be seen as a generalization of the Hopfield model. The Boltzmann machine itself is fully connected, but due to the excessive number of connections that need to be processed, it is not very practical. It was later transformed into a restricted Boltzmann machine, distinguishing between hidden and input layers. Although Hinton was not the original inventor of the restricted Boltzmann machine, his contributions cannot be ignored; in fact, he rediscovered this model and proposed a training method called contrast divergence, making the Boltzmann machine truly usable. Contrast divergence is a complex iterative process, but some of Hinton’s work made it feasible. Thus, I look forward to Professor You Yizhuang further discussing Hinton’s contributions to contrast divergence and sampling.
You Yizhuang: Hinton’s work is actually an advancement of the Hopfield model; he elevated the Hopfield model to new heights. The core goal of this generative model is to learn an energy function that represents the probability density distribution of samples. All generative models need to be trained based on samples.
But how to train the Boltzmann machine becomes a problem. Hinton thought of some very clever methods for training; his basic idea is this: if we use some energy function as a model to generate a probability density distribution, and the samples themselves also have their own probability density distribution. In principle, we hope that these two probability density distributions are as close as possible, that is, to make the model’s distribution as close as possible to the sample’s distribution. We need to minimize a quantity called KL divergence—representing the relative difference between the two distributions. After some research, he found that relative entropy can basically be expressed as: the difference between two free energies.
This is actually a very interesting point. Imagine that if we let the model run with its eyes closed, it will produce a free energy of a statistical mechanical system, which represents the system’s energy in some average sense. When there are sample data in the visible layer, we call this “claimed free energy,” and when data is forcibly loaded into the visible layer, the model will also have a free energy. The difference between these two free energies is exactly what the KL divergence represents as the loss function.
This points us in a training direction, as if the relationship between closing and opening our eyes. During the training process, you can first let the model close its eyes and imagine. Suppose I have a bunch of spins, some of which belong to the visible layer, and they need to be consistent with the data; the others belong to the hidden layer, which is not important for them. During the closed-eye phase, we observe how strong the correlations are between the visible layer spins, which is what the model imagines or “dreams” during its process. Then, when data is present, the model will again observe the visible layer data, studying how strong the correlations are between the visible and hidden layers when the visible layer data is fixed and the thermodynamic system reaches equilibrium. For example, in a restricted Boltzmann machine, we only need to care about the correlations between the visible and hidden layers. Therefore, we only need to compare the strengths of correlations in the presence and absence of data to determine whether the connection between the visible and hidden layers should be strengthened or weakened. If the correlations are weaker when data arrives, and stronger in the absence of data, it indicates that the system’s imagination does not match reality, thus the coupling strength between them should be reduced to achieve this. This is the basic idea of contrast divergence.
It is similar to our usual learning process, where we have both textbook learning and closed-book thinking. As Confucius said, “Learning without thinking is labor lost; thinking without learning is perilous,” meaning learning and thinking should be combined. I believe the idea of contrast divergence very well embodies the combination of learning and thinking processes. When data comes in, you need to learn to reach a certain balance, and you also need to think, then compare the differences between learning with open and closed eyes to adjust your neural network weights.
Of course, this process involves steps of thermal equilibrium. When data is input, we need to achieve thermal equilibrium for the entire system based on the data, which means going through repeated sampling iterations to bring the spin system to equilibrium. In the closed-eye thinking phase, multiple sampling iterations are also necessary. This involves considerations of computational complexity. Early algorithms were not very successful, partly because using Monte Carlo sampling methods on spin models required substantial computational resources. Hinton made a very important observation: in fact, you do not need to let the two systems reach thermal equilibrium. Although mathematically, you should compare the correlation strengths between equilibrium states, we can actually already see the differences in correlations between the closed and open eye states—i.e., in the presence and absence of data—this can already provide some learning signals. Hinton also proved that even if you follow such an incorrectly complete signal, the minimum point of the loss function will be the same as the original minimum point. This allows us to sample and learn more efficiently. These ideas transitioning from equilibrium to non-equilibrium physics are very interesting thoughts in statistical mechanics. I believe these are all valuable for us to think about and learn from.
Zhang Jiang: Hinton has played two key roles as a savior in the history of neural network research. The first time was around the 1980s. Before that, since the inception of artificial intelligence in 1956, the mainstream was traditional AI focused on search and logical reasoning. Although the concept of neural networks can be traced back to the mathematical model proposed by Warren McCullough and Walter Pitts in 1943, Minsky and Papert proved in their book “Perceptrons” that single-layer perceptron models could not solve simple XOR and other linearly inseparable problems, which nearly killed the neural network discipline. During that period, researchers feared their papers would not be published, and the neural network discipline was on the brink of extinction. However, it was Hinton who persisted in neural network research and successfully applied the backpropagation algorithm to train multi-layer neural networks, marking the first time he saved the neural network discipline.
The second rescue occurred during the early stages of deep learning. At that time, although neural networks were performing well in many learning tasks, their limited depth restricted the problems they could solve. Therefore, many people were not optimistic about neural networks, and there were many competing algorithms. Hinton demonstrated the potential of deep neural networks by making restricted Boltzmann machines very deep, and according to my recollection, he may have been the first to use the term “deep neural network” in a 2006 paper. This made people realize that it was not that neural networks were ineffective, but that we had not made them deep enough. When we deepened them, they really worked well and achieved excellent results. Initially, they made significant breakthroughs in speech recognition and image recognition, allowing more people to see that we could use deep learning to enable artificial intelligence to learn entirely through deep means and achieve very good results.
Hinton’s first key breakthrough in the history of neural network research: applying the backpropagation algorithm to multi-layer neural network training
Rumelhart, D., Hinton, G. & Williams, R. Learning representations by back-propagating errors. Nature 323, 533–536 (1986). https://doi.org/10.1038/323533a0
Hinton’s second key breakthrough in the history of neural network research: proposing deep neural networks
Hinton, Geoffrey E., Simon Osindero, and Yee-Whye Teh. A fast learning algorithm for deep belief nets. Neural computation 18.7 (2006): 1527-1554. https://direct.mit.edu/neco/article-abstract/18/7/1527/7065/A-Fast-Learning-Algorithm-for-Deep-Belief-Nets
Hinton, G. E., & Salakhutdinov, R. R. (2006). Reducing the dimensionality of data with neural networks. Science, 313(5786), 504-507.
– 3 –
What is the connection between machine learning and statistical physics?
You Yizhuang: I believe that the close integration of physics and artificial intelligence is largely due to the fact that physics essentially tries to model reality, and AI also largely aims to model reality. What is reality? Reality is the data we want to learn. What is modeling? It is the model we want to train AI on. Therefore, their objectives are consistent in many cases. For this reason, many mathematical models developed by physicists during their long-term modeling of the world are worth borrowing in the AI field.
In fact, we can see that many current generative models have borrowed ideas from physics. For example, the energy-based generative models that won the Nobel Prize in Physics this year, as well as flow-based generative models, which relate to physical concepts such as probability flow and incompressible fluids. There are also diffusion-based generative models that relate to diffusion processes in physics. Even in the field of quantum physics, quantum mechanical models have been proposed, such as tensor networks, where Professor Wang Lei has pioneering work in this area. Especially in the field of deep models, our main task is to model the world, but unfortunately, the world is random, so we must model probability densities and probability distributions.
When modeling probability distributions, two major disciplines in physics related to probability distributions come into play: statistical mechanics and quantum mechanics. These two fields each have a set of methods for modeling probability distributions. Since probability distributions must be positive definite numbers, we cannot arbitrarily design a neural network and then claim that the output of this network is a probability distribution. The outputs of neural networks do not guarantee positivity, so statistical mechanics adopts a method: using the Boltzmann distribution. This method first constructs an energy function and then exponentiates it, mapping any real number to a positive probability. In quantum mechanics, the wave function is constructed. The wave function itself does not require positivity, but by taking the square of its modulus, we can also obtain a positive probability distribution. These modeling ideas may sound like simple techniques, but in fact, they can all be applied to machine learning. There are various small techniques scattered throughout the literature or textbooks in physics, and I believe drawing experience from them is very helpful for us to enter the field of machine learning.
A Generative Model for Physicists. Wang Lei, Zhang Pan, “Physics” 2024, Issue 6
Zhang Jiang: Another interesting point I find is the close connection between the “depth” of deep neural networks and the renormalization group in physics. This connection can be understood as when we continuously propagate signals to higher layers, we are essentially observing the same system from a more macroscopic perspective, a broader scale. Therefore, deep learning is essentially a form of multi-scale learning. This characteristic of multi-scale learning is formally similar to the renormalization group. In some networks, such as convolutional neural networks (CNNs), we can also see that the features extracted from shallower to deeper layers inherently possess this multi-scale characteristic. Of course, the connection to the renormalization group may be just one aspect; there may be more connections. We can further think about what connections deep learning has with this issue in statistical physics or more broadly in the field of physics.
You Yizhuang: I am very willing to delve into the topic of the renormalization group, as it is one of my main research directions. I would like to expand on this point. Traditionally, the renormalization group is a very effective tool for understanding complex systems. Its core idea is to first coarse-grain a complex system locally, then extract the most important features, and think about how these features interact at larger scales, thereby extracting effective interactions. In this way, we build an effective model, which can be further simplified based on the effective model, extracting even more effective models, allowing the system to be gradually analyzed.
However, how to extract effective features has always been a problem, and there has not been a very clear or unified approach for a long time. Often, it relies on outstanding physicists like Leo Kadanoff to propose renormalization schemes. Some of the research in our team aims to utilize machine learning methods, especially the important function of restricted Boltzmann machines, which is to extract features; it can extract key features from observed, more detailed samples through representation learning.
Coarse-grained feature extraction can be seen as an example of deep learning applied in physics. Applying deep learning to the physics field can indeed solve some physical problems. We design renormalization algorithms based on deep learning and can genuinely apply them to statistical mechanical models. In physics, the questions we want to answer are often quantitative problems, such as what the critical exponent is during phase transitions in these statistical mechanical models, or how the spin correlation function decays exponentially during phase transitions. These are questions physicists are very eager to answer. If we can develop better renormalization schemes, we can quantitatively answer these questions. Although most deep learning applications currently focus on image and language processing, which seem to be qualitative applications, generative models and deep learning can also yield quantitative results in scientific research. Our research papers show that these algorithms can provide increasingly precise methods to determine critical exponents in physics. This is an example of artificial intelligence applied in physics. AI development provides us with new tools, allowing us to quantitatively answer some questions that may have only been qualitatively answered before, which is beneficial for quantitative science.
Conversely, physics also helps AI in many ways, and statistical physics itself contributes greatly to understanding the principles of deep learning. Scientists like Dan Roberts have studied why deep neural networks can learn, employing some quantities from statistical physics, particularly techniques from quantum field theory, to understand how networks behave as the number of neurons approaches infinity. These behaviors can be understood using statistical physics methods because statistical physics aims to understand the limit case of particles in many-body systems approaching infinity. Therefore, when the number of neurons in a neural network approaches infinity, it will also exhibit behaviors that can be treated by statistical physics, providing some theoretical support for understanding how neural networks work. For instance, in these studies, the neural scaling law was discovered, which revealed how to initialize neural network parameters and what the Gaussian width should be for initializing each layer to ensure the neural network is in the theoretically optimal state for learning and training. I believe that both AI for Physics and Physics for AI are mutually reinforcing.
Roberts, Daniel A., Sho Yaida, and Boris Hanin. The principles of deep learning theory. Vol. 46. Cambridge, MA, USA: Cambridge University Press, 2022.
-
What is the connection between facial recognition and the universe? See how physicists use renormalization group flow models to reinterpret vision
-
Renormalization group meets machine learning: A multi-scale perspective exploring the inherent unity of complex systems
-
The interdisciplinary connections of complexity: fractional calculus, renormalization group, and machine learning
– 4 –
How do the developments in AI and science empower each other?
Q: Much of what we discussed earlier was from the perspective of physics. We know that besides Physics for AI or Science for AI, there is also a corresponding field, which is AI for Science. Current AI tools can already be applied to many scientific problems. For example, this year’s Nobel Prize in Chemistry was awarded to the developers of AlphaFold, who solved a long-standing difficult scientific problem—the prediction of natural protein structures. I would like to ask the teachers, what broader applications could AI have in the field of AI for Science?
You Yizhuang: I believe AI for Science is already widely popular across the scientific research field, just like when computers emerged, everyone wanted to use computers for science. Now, I think AI’s applications in science can be summarized in the following points.
First, AI and neural networks can assist humans in providing a variational guess for science. Because neural networks can fit various functions, in science, we often face the unknown and need to propose hypotheses. Human imagination is limited, so we need AI to help us propose hypotheses. In this area of work, for instance, some have proposed using neural networks to construct quantum wave functions, optimizing quantum wave functions to calculate the ground state solutions of various molecular or many-body quantum systems, thus understanding complex materials and designing various drugs, etc. These applications are very valuable.
On the other hand, AI has the potential to replace the so-called computational bottleneck. In scientific research, many fields require large-scale simulations, and these simulations often come at a high cost, consuming substantial computational resources. Many times, people hope to adopt an end-to-end approach. Simulations are often a process akin to climbing a mountain: the input conditions are relatively simple, and the answers are not difficult to obtain, but the intermediate processes are extremely complex. If you repeat this process multiple times and accumulate enough data, you can train AI to replace the intermediate steps in this climbing process, which are the parts where computational complexity first increases and then decreases. In this way, AI can directly create a computationally flat tunnel, which is AI’s second use, namely replacing bottlenecks in computation, which is also very useful in science.
The third is AI-assisted data mining. Taking high-energy physics as an example, at CERN (European Organization for Nuclear Research), scientists conduct a large number of experiments daily, colliding atomic protons, hoping to discover whether particle physics has new violations of the standard model from the data of these high-energy collisions. However, the standard model is already quite mature, and we want to discover new physical phenomena, which is like searching for tiny signals in a huge noise background. Particle colliders generate massive amounts of data every moment, and if we record all of it and analyze it one by one, first, there won’t be enough storage space, let alone the computational resources required for analysis. Many times, we need to determine whether a collision event is worth recording in real-time at the collider, a process known as “triggering,” in their terminology, the “trigger.” They need to develop AI algorithms to mine signals directly from the collider and in the big data, using these signals to trigger all subsequent processes. This is also true in astronomy; for example, the discovery of the black hole photo, which caused a stir and later won the Nobel Prize, utilized AI technology in processing those astronomical images. Therefore, AI plays an important role as a data mining tool in data processing.
So, I believe that AI, as a tool for variational hypotheses, a means to replace computational bottlenecks, and a tool for data mining, has already matured in these three application areas and has been widely applied. However, I think one thing that AI currently struggles to achieve is that we cannot expect it to conduct research like a graduate student, planning research projects in dialogue with mentors. The development of large language models has shown us some hope in this area, but this hope does not seem to be as great as initially imagined. I believe we still need to wait patiently in this regard. Whether this requires some kind of integrated effect, whether multiple AIs need to work together to form a social structure, or whether the paradigms we are currently training with are problematic, making this process unsustainable. Perhaps we need more innovative ideas to truly enable AI to communicate with humans in scientific discoveries or even replace humans in making new scientific discoveries.
Zhang Jiang: In this regard, I believe AI may bring about a paradigm shift in scientific research. The natural sciences we are familiar with, especially fields like physics, have traditionally adopted a paradigm that spans from Tycho Brahe to Kepler, then to Newton, and can even add Einstein. That is to say, first, like Tycho, starting from data and performing data mining work. Then, Kepler’s greatest contribution was to propose a descriptive model that could summarize a set of data with some equations, but these were not mechanistic models. Newton’s greatest contribution was that he proposed three laws of motion, discovering that celestial bodies and earthly objects, like cars and apples, all follow the same set of equations, thus finding more fundamental laws. Einstein reached a more abstract level, achieving a level of spacetime symmetry to explain all these phenomena. This is a traditional scientific research paradigm.
But now we are facing many systems that are not so simple; they may be very complex, such as meteorological systems, or even the entire Earth’s climate models. For such complex systems, it is difficult to abstract and establish models according to traditional methods to explore the ultimate symmetries. In this case, artificial intelligence, especially large language models, provides us with a new possibility: a data-driven approach that understands the entire dataset through learning neural networks with a large number of parameters. This will create a confusion, as these models with a large number of parameters are difficult for us humans to understand, unlike traditional physics where we can write out an equation and understand the principles behind it. But now it is not possible; the explainability of artificial intelligence has become a huge bottleneck. In response to this problem, we may have two ways to cope with it:
One approach is to accept this status quo, not seeking explanations, directly moving from large parameter models to large parameter models. In fact, the current large language models do just that; no one knows what the beautiful equations behind language are or what the symmetry principles are, and we may not know at all, but that doesn’t matter; we can handle and simulate human language ability very well. This is one way to abandon explainability. The other approach is to develop some tools and methods for explainability, allowing models to extract principles that we humans can understand. I think this is also a possibility worth exploring.
In summary, the emergence of this new tool, AI, as You Yizhuang said, is like the emergence of computers in the past, but it may even be more powerful; it can be deeply embedded in our scientific research.
Tang Qianyuan: I would like to add that this is also related to the upcoming discussion on explainability. I want to share two new attempts I have made in this regard. The first idea is that now there are so many people developing AI, which generates massive amounts of data, yet no one analyzes the data generated by AI. My idea is that instead of having AI act like Kepler or Newton, let AI act like Tycho, while we humans become Kepler and Newton, analyzing the data generated by AI to discover new physical laws. For instance, in the field of protein structure prediction, we have now completed the genome sequencing of humans and various animals, and we humans can conduct statistical physics research based on that. I believe this is an angle to open the black box of AI; we are not opening AI’s black box, but rather looking at the statistical physics of the results learned from AI to understand what AI has actually learned.
Another angle is that we do not open the black box of AI, but when using AI tools, we do not just ask one question; sometimes we also give it some prompts. For example, asking “Why is the sky blue?” you might say, “Assume you are Feynman, please explain why the sky is blue,” or “Assume I am a five-year-old child, please explain to me why the sky is blue.” Different prompts can yield different answers. Similarly, protein structure prediction tools will not only utilize the structure sequences of the proteins they are to predict but also reference ancestral sequences similar to those sequences. This process is somewhat like inferring interactions based on correlations; we can treat the ancestral sequences as a type of prompt, providing AlphaFold with this part of the sequence to allow it to predict this structure, and giving it another part of the sequence to predict another structure. AI will predict different protein structures under different prompt conditions, indirectly solving protein dynamics with AI. Thus, we are no longer engineers of AI, but prompt engineers, designing prompts for AI; although we do not open the black box of AI, we ultimately still open the black box of AI. (See: “AI+Science New Perspectives: Using Physical Information to Guide AlphaFold 2 in Predicting Protein Dynamics”)
 Figure 2. When AI can generate data like Tycho, humans can act like Kepler to analyze the data generated by AI to discover new physical laws. | Excerpt from Professor Tang Qianyuan’s report
Figure 2. When AI can generate data like Tycho, humans can act like Kepler to analyze the data generated by AI to discover new physical laws. | Excerpt from Professor Tang Qianyuan’s report
– 5 –
What insights can statistical physics and complex systems provide for the field of artificial intelligence?
Q: Currently, the AI field mainly applies statistical physics, but we know that there are many developments in physics after statistical physics, including quantum mechanics, quantum field theory, and now frontier fields. I wonder if these physical theories could also be applied to AI architecture design in the future?
You Yizhuang: I think to a large extent, the development of AI is continually integrating various mathematical tools. For instance, feedforward neural networks achieve mappings of arbitrary functions; recurrent neural networks (RNNs) handle time series processing, similar to dynamic equations in physics; and models like Neural ODE achieve solutions to differential equations, including automatic differentiation and feedback functions. All of these are based on advanced mathematical concepts. We naturally look forward to more advanced mathematical tools being introduced into AI. When we talk about deeper physics, it often involves complex mathematics, such as category theory, topology, and other algebraic and topological fields. These mathematical tools may also be applied to the design of neural network architectures, and people are making some attempts in this area.
Overall, I believe this relates to the insights from this Nobel Prize. The two awardees applied physics to the design of learning algorithms, thus opening a new chapter in the entire field of AI. As latecomers, if we want to further develop based on their foundation, we naturally need to borrow more mathematical knowledge that they have not yet introduced into the AI field, which is a goal. More specifically, as mentioned earlier, quantum mechanics is currently a very hot topic. For instance, in the United States, there will be a conference next spring specifically discussing the combination of AI and quantum. The combination of quantum computing and artificial intelligence is very natural because they share a common topic—information. Discussions on how to process information, how to use AI to help us build quantum computers, and how to use quantum algorithms to improve AI algorithms are currently hot topics.
2025 AI+Quantum Conference
https://sites.google.com/view/quai-acp-2025/home
Tang Qianyuan: In fact, there are many connections between statistical physics, complex systems, and machine learning. First, as You Yizhuang just mentioned, what we call deep learning includes not only structures represented by deep neural networks but also recurrent neural networks, which can be described using tools from complex systems, which are also the subjects of complex systems research. In addition, some tools from the complex systems field, such as reservoir computing, can also be used to help us analyze fundamental theoretical issues in these models. There are also recently very popular diffusion models and large language models; everyone is discussing some fundamental theoretical issues in these models, and physicists can contribute more to these issues.
However, I want to ask a question, which is not my original idea. When the Nobel Prize was just announced, Professor Zhang Pan from the Institute of Theoretical Physics at the Chinese Academy of Sciences raised a point in his report, suggesting that the initial connection between deep learning or machine learning and statistical physics was very tight, but now it seems to be getting further apart. So I would like to ask both professors, is there a possibility that at some point in the future, they may reconvene, or in which areas might they merge again?
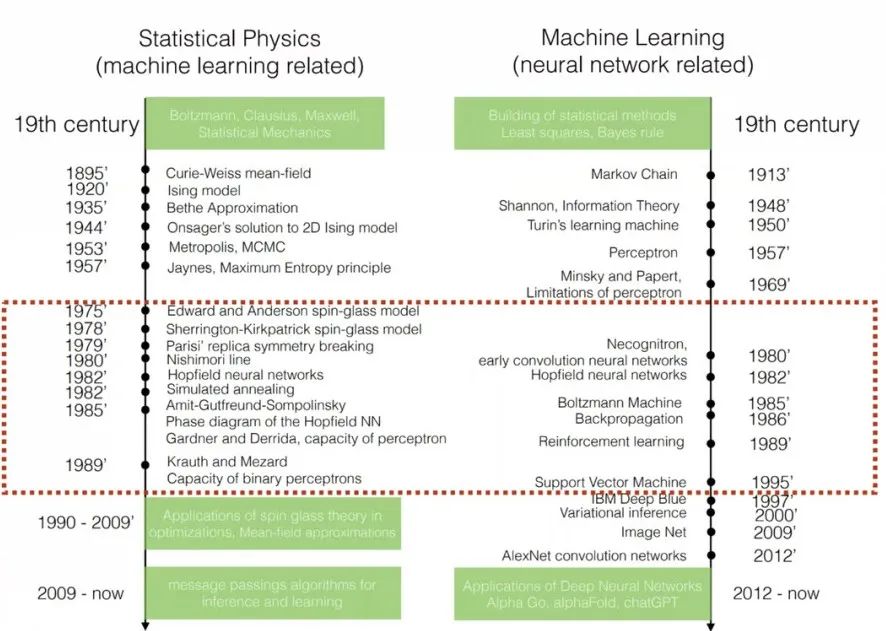
Figure 3. The connection between machine learning and statistical physics. | Excerpt from Professor Zhang Pan’s report
You Yizhuang: I believe that the content listed in Professor Zhang Pan’s table relates to statistical physics concerning spin models and spin glasses, but statistical physics encompasses much more than these; it also includes non-equilibrium statistical physics. A very important part of non-equilibrium statistical physics is the Fokker-Planck equation and the Langevin equation, which describe stochastic processes, and stochastic processes are the basis of current diffusion models. Therefore, in my view, we cannot say that machine learning and statistical physics are getting further apart; on the contrary, they are becoming more deeply integrated and increasingly merging with more fields.
Zhang Jiang: From another perspective, as mentioned earlier, complex systems, especially after the emergence of large language models, may present many phenomena that will require the tools of physics for explanation. There are two typical phenomena: one is the so-called scaling law, and the other is emergent abilities. Currently, there is no very good explanation for these two phenomena, and they are typical characteristics of complex systems. When we observe any complex system, such as cities or biology, we can see that as the scale increases, various indicators exhibit power-law scaling. In neural networks, OpenAI’s willingness to bet on large models stems from the strong predictability of scaling laws; when we scale the model to a certain extent, the loss will inevitably decrease to a certain level. But this is only a small part of many scaling laws. Now, it may also exhibit corresponding scaling laws in the reasoning phase after training. We know that scaling laws are a typical hallmark of critical phenomena, indicating that neural network models ultimately become complex systems, which must be critical systems far from equilibrium. Understanding such systems may provide corresponding tools from statistical physics, and currently, there is no deeper understanding. Therefore, I believe these are all very important points for the future close integration of the two fields.
– 6 –
Will AI surpass human understanding to discover new physics?
Q: Is it really possible for AI to help us discover new physical phenomena or new mechanisms? Or does AI’s strength not lie here, and human participation is still needed?
You Yizhuang: I think this is a very good and important question. AI currently appears to be somewhat distant from the general artificial intelligence (AGI) we pursue, so many people are asking where the path to AGI lies. I once heard Professor Qi Xiaoliang talk about this, and many people have exchanged views on this concept, which involves the notions of System 1 and System 2. System 1 is an intuitive response system, while System 2 requires reflection and modeling of the world. I believe the process of AI discovering new physics is actually a journey from System 1 towards System 2. Many times, human rational thinking abilities stem from predictions about the world; when the predictions are contradicted by reality, it causes discomfort, leading to rational reflection. Therefore, how to train AI to predict the world and build a model of the world is a very important question. Previously, the focus was more on representation learning, akin to describing the world, or more on how to encode. Now, we also need to learn how to predict, focusing more on how events evolve and how actions we take will change the world and what causal effects they will have. Therefore, these questions may be directions that AI needs to pay more attention to in the future.
As a physicist, I believe that physics laboratories provide a good platform for AI, allowing it to interact with experiments and reality in the laboratory. Perhaps we cannot directly let AI roam freely on the streets, as that would be dangerous, but we can let AI conduct chemical experiments and physical experiments in a controlled scientific laboratory environment, allowing it to learn the laws of nature and the laws of natural sciences, enabling it to model natural sciences. I believe this is a necessary pathway for AI to learn physics and discover new physical laws.
Related articles: “Time, Information, and Artificial Intelligence: Looking at the Future of Large Models from the Perspective of Information Dynamics”
Zhang Jiang: I completely agree with Professor You Yizhuang’s viewpoint that AI needs to understand the physical world more. In modern society, the world we face is full of complexity and uncertainty. Additionally, I believe another possibility may emerge, which is related to the development of large models, especially the multi-modal large models being developed by many large companies. Now, models can learn language, images, and even audio and video simultaneously. By consolidating these multi-modal data, we can have a unified representation, whether for building models of the world or for understanding it.
Therefore, I foresee that there may be such a possibility in the future, which relates to the discussions between the two of you: AI may discover some common laws between fields that are difficult for humans to handle. For example, while learning meteorological models, it may also learn economic models. If we train a larger model using data from both sides, it is very likely to find common laws across different fields. This is precisely the goal of complex science: to explore whether there are some unified laws behind complex systems. However, due to the limitations of the human brain, it is difficult for us to find this unity. In the future, in large models, artificial intelligence may learn these laws by itself. However, at that point, the issue of explainability arises again, as AI may discover new physics but finds it hard to explain clearly to us. Therefore, we may need to study its data or the model itself to unveil this layer of mystery. It is very likely that such a situation will occur.
Tang Qianyuan: Just now, Professor You Yizhuang mentioned the issue of being “slapped in the face,” meaning that why we feel surprised by some predictions is because they contradict what we expected to happen. Therefore, some people have proposed the free energy principle to explain how human or intelligent agents perceive and explore the world, suggesting that this may be the basis of consciousness formation. So, is it possible that this is another method for discovering physics? I would like to ask Professor Zhang Jiang to elaborate on this point.
Zhang Jiang: The free energy principle may greatly assist us in understanding intelligence. Some people say that the free energy principle is, in some sense, the first principle of intelligence, and there is a certain possibility to that. The greatest inspiration it gives us is that intelligent systems are actually the result of a dual combination of the internal and external. Currently, our data-driven AI models emphasize directly acquiring experience from data, possibly not paying much attention to innate structures. However, we know that the human brain has innate structures; for example, we are sensitive to symmetry, and when we see something symmetrical, we get excited, especially in physics, where we love pursuing higher levels of symmetry, which may stem from some innate structure of intelligence. Therefore, the learning process is not merely a passive one where it is trained by external data; many times, it involves mutual training between its innate structure and external data, which influences each other.
So I believe that current artificial intelligence has explored this aspect relatively little, especially the impact of the innate structure of intelligence on the final outcome. This is a very interesting question. I am very interested in this question because I believe that many AI networks, at initialization, do not conform to biological or physical principles. In nature, some simpler physical mechanisms produce initial structures, which then evolve. Although these structures may not perform as well in certain machine learning tasks, they have some advantages, such as low energy consumption, requiring less energy to execute complex tasks, which is another manifestation of intelligence. For instance, while humans cannot surpass machines in Go, the human brain consumes less energy. From this perspective, the constraints of natural laws may play an important role in helping reduce training costs or transfer difficulties, or in having stronger multi-modal capabilities, etc. These aspects may require us to have more theoretical explanations and research.
You Yizhuang: I feel that today’s AI lacks culture. In fact, much knowledge is solidified in human social culture. For example, the importance of symmetry mentioned earlier may be due to the influence of education about symmetry, emphasized repeatedly by mathematics teachers, or through experiencing its beauty. This culture can solidify in structures, passed down from generation to generation, becoming a kind of belief. However, today’s AI seems to lack this belief; it goes wherever the data points, and it cannot form its own belief. I think this is a problem we need to think about: how to let AI form its own beliefs.
– 7 –
What will be the next Nobel Prize-worthy scientific research?
Q: After the 2021 Nobel Prize in Physics was awarded to researchers studying complex systems, and this year to those in AI research, we can’t help but wonder if there will be more astonishing research related to complex systems and AI that could win the Nobel Prize in Physics in the future?
Zhang Jiang: I want to share my personal view first. I believe that while current AI research is very hot, it is still relatively limited to individual intelligence. Even if we have larger models, they are merely large parameter models owned by companies. I believe that in the future, these models themselves will become more distributed and multi-body. Why do I say this? Because I observe that although AI is developing rapidly, it still cannot solve most of the major problems we face in the material world, such as the current major issues including the energy crisis and climate crisis. The entire Earth may undergo significant changes due to rising temperatures, which is very concerning. However, current AI development has little research directed towards this area, so I believe there is vast room for improvement in this field. For example, today I noticed that traffic issues are very severe. In the future, if autonomous driving technology is widely applied, it may optimize everyone’s travel, reducing much energy waste. Of course, there are many related fields, including logistics, people’s travel, and the production and consumption of materials, all of which have significant room for improvement.
Could future AI research be more interdisciplinary, helping us make the flow of physics, materials, and energy in human society more efficient? I believe this would be of great significance and could be a Nobel Prize-worthy research area. I wonder what everyone thinks about this?
You Yizhuang: I believe that if we achieve room-temperature superconductivity, it would undoubtedly be a Nobel Prize-level achievement. Similarly, if controllable nuclear fusion is realized, that would also be a strong candidate for the Nobel Prize. From the perspective of physics, I think the quantum information field is likely to win one or two more awards, as the progress in this field is indeed significant and has become a research focus across many disciplines. As for the field of quantum gravity, it may also receive awards. For example, this year, several scientists proposed concepts of gravity related to quantum entanglement and spacetime duality and have already received an award just below the Nobel Prize. Therefore, I believe that more Nobel Prize-level research is likely to emerge in the fields of quantum mechanics, quantum information, and deepening our understanding of spacetime.
Tang Qianyuan: I believe that AI’s assistance in finding common viewpoints is worthy of a peace prize. There are many various possibilities; recently, I saw an article, possibly in “Nature” magazine, discussing how we can use AI to resolve conflicts and promote communication. For example, when there are differences between two parties, AI can conveniently find common points in both viewpoints, helping us reach a better consensus. In this sense, AI’s contributions could possibly be nominated for a peace prize.
You Yizhuang: Then GPT is completely worthy of the Nobel Prize in Literature.
Q: Can AI explain complexity?
Zhang Jiang: Currently, research on complexity is still relatively scarce, as we do not need to deeply understand what complexity is; AI’s style is to directly tackle it. Historically, there have been more than twenty quantitative definitions of complexity, and there has been much debate on this topic. However, one common point is that complexity is closely related to information, thermodynamics, and statistical physics. This shows that complexity itself is rooted in the fields of information computation and is closely related to physics and statistics, thus its relationship with AI is also very close.
Q: Since large models construct potential functions, can we extract the trained potential functions to explain AI?
You Yizhuang: This is a pretty good idea. However, the parameters in large models are too many, and many times we are not clear how they arrive at their answers. Some thoughts have already emerged in this regard. For example, in a project I previously collaborated on, we proposed an idea: perhaps we can use a second AI to analyze the thought process of the first AI. The first AI, which we call task AI, is responsible for processing data, only needing to complete the transformation task from data A to data B. During its training process, it will form its own neural network parameters, and these parameters, along with the neural activity of the neural network, can also serve as training data for the second AI to learn the thought processes of the first AI. For instance, the second AI can attempt to compress or learn representations from the neural data of the first AI. You can imagine this process can continue to nest, just like Russian dolls, where the second AI can nest into a third AI.
Therefore, I believe that in the current AI field, we are beginning to see some work where small AIs operate nested within large AI models, which may be a trend for future development. For example, the recently popular sequence model TTT (Test-Time Training) embeds small transformers into large transformers. I believe that using AI to analyze AI, rather than relying on humans to analyze AI, may be a pathway to improve explainability in the future.
Sun, Yu, et al. Learning to (learn at test time): Rnns with expressive hidden states. arXiv preprint arXiv:2407.04620 (2024). https://arxiv.org/abs/2407.04620
Q: We observe that the machine learning field has experienced a scale effect of big data, which enables the training of large models. It may also bring about reasoning scale effects. So, where will the next scale effect appear? Will it be AI creating AI, or multiple AIs working in collaboration?
Zhang Jiang: If we step outside the AI circle and look from a non-expert perspective, a significant observation is that it has expanded the bandwidth of human-machine interaction. Traditionally, this bandwidth was limited by screens, mice, and keyboards, which were very serial. But now, we have natural language processing and multi-modal interactions, meaning we can interact with computers in various ways. Don’t forget, the person standing in front of the machine is itself a naturally complex intelligent agent, hiding profound things and massive unknowns. I believe that if there is further development in the future, it is likely to occur in this bandwidth of human-machine interaction. When the bandwidth expands to a certain extent, it may trigger some kind of mutation, and perhaps in some sense, telepathy will emerge. One thought, and the machine captures your micro-expressions; you may not even need to speak, and you may not even be aware that your eyes blinked, but the machine already understands, and at that time, it may provide some services for you. I believe this is the real future, rather than simply developing the capabilities of machines, which is very cool.
You Yizhuang: I completely agree with this viewpoint. I believe an important scaling effect in human society lies here. The power of individual units is limited, but our society has developed human civilization; the continuous transmission of this civilization is where the true entity of intelligence in human society resides. I think AI is similar; the next scaling effect in AI will be reflected in the formation of AI networks, where AIs form a complex network of interactions. In this complex system, as the number of AIs N approaches the thermodynamic limit, that is, when the number is extremely large, AI will form a society, transitioning from individuals to socialization. At the same time, AI society and human society will be closely linked through human-machine interactions. This social scaling effect may be the next scaling effect.
Zhang Jiang: To add, if you review the history of AI development, it is actually very interesting. It has been cycling back and forth between individual intelligence and multi-body intelligence, iterating continuously. In the early days, for example, when the AI discipline was founded in 1956, the goal was to endow machines with strong reasoning capabilities. By the 1980s and 90s, the Santa Fe school emerged, and one of their significant contributions was the shift toward multi-body intelligence, achieving breakthroughs through the collaboration of many intelligent agents. Now, with the breakthroughs of deep learning large models in individual intelligence, the future will certainly be an era of large-scale multi-body intelligent cooperation.
Our discussion today actually started from physics. To describe such complex systems, we certainly need updated statistical physics, requiring statistical physics to have more breakthroughs, whether in the context of statistical physics for multi-modal information processing or in the interactions of multiple intelligent agents. This could bring many new questions that may be incorporated into the research scope of physics. We have already seen that some challenges in the machine learning field may be addressed using statistical physics as a tool. In the future, as we imagined, more questions may arise, and various tools from statistical physics, complex systems, and so on may be applied to this field.
We invite friends interested in further learning to scan the QR code below to watch the complete video replay.
https://pattern.swarma.org/study_group_issue/796
Non-Equilibrium Statistical Physics Reading Group Launched!
The 2024 Nobel Prize in Physics is awarded to artificial neural networks, a revolution in machine learning triggered by statistical physics. Statistical physics not only explains thermal phenomena but also helps us understand how various levels from microscopic particles to the macroscopic universe are connected, and how complex phenomena emerge. By studying the collective behaviors of large numbers of particles, it successfully links the randomness of the microscopic world to the determinism of the macroscopic world, providing a powerful tool for understanding nature and significantly driving the development of machine learning and artificial intelligence.
To explore the cutting-edge progress of statistical physics, the Intelligent Club, in collaboration with the School of Science and the Interdisciplinary Science Center at Westlake University, along with Professor Tang Leihan, Chair Professor of the Department of Chemistry and Physics at Stony Brook University, Professor Wang Jin from the Dresden Systems Biology Center, Postdoctoral Researcher Liang Shiling, Assistant Professor Tang Qianyuan from the Department of Physics at Hong Kong Baptist University, and many well-known scholars from home and abroad, jointly launched the “Non-Equilibrium Statistical Physics” reading group. The reading group aims to discuss the latest theoretical breakthroughs in statistical physics, its applications in complex systems and life sciences, and the intersection with cutting-edge fields such as machine learning. The reading group will start on December 12, meeting every Thursday from 20:00 to 22:00, expected to last for 12 weeks. We sincerely invite friends to participate in discussions and explore the universal theory envisioned by Einstein!
Recommended Reading
1. 2024 Nobel Prize in Physics awarded to artificial neural networks: A machine learning revolution triggered by statistical physics
2. Why was the 2024 Nobel Prize in Physics awarded to the field of machine learning?
3. Physics meets machine learning: The next breakthrough in deep learning may come from statistical physics
4. Zhang Jiang: The Foundation of Third-Generation AI Technology—From Differentiable Programming to Causal Reasoning | New Course at Intelligent Academy
5. Dragon Year brings good fortune; now is the time to learn! Unlock all content at Intelligent Academy and start your new year learning plan
6. Join Intelligence; let’s explore complexity together!
Click “Read the original text” to register for the reading group