| Full text is 4175 words, estimated reading time is 4 minutes |
This article is authorized to be reprinted by Machine Heart (WeChat public account: almosthuman2014), and secondary reprinting is prohibited.
Excerpted from: arXiv
Translation: Machine Heart
Contributors: Huang Xiaotian, Lu Xue, Jiang Siyuan
Recently, researchers from Nanyang Technological University published a paper describing the mathematical principles of convolutional networks, which elaborates on the operations and propagation processes of convolutional networks from a mathematical perspective. This paper is very helpful for understanding the mathematical essence of convolutional networks and assists readers in implementing convolutional networks “from scratch” (without using convolution APIs).
Paper link: https://arxiv.org/pdf/1711.03278.pdf
In this paper, we will explore the mathematical essence of convolutional networks from aspects such as convolution architecture, component modules, and propagation processes. Readers may be familiar with the specific operational processes of convolutional networks; beginners can first refer to the first part of the Capsule paper interpretation to understand the detailed convolution process. However, we generally do not focus on how convolutional networks are mathematically implemented. Since major deep learning frameworks provide concise convolution layer APIs, we can construct a variety of convolution layers without needing mathematical expressions; we only need to pay attention to the tensor dimensions of the input and output of the convolution operation. Although this allows us to perfectly implement networks, we still lack clarity on the mathematical essence and processes of convolutional networks, which is the purpose of this paper.
Below we will briefly introduce the main content of the paper and attempt to understand the mathematical process of convolutional networks. Readers with a background can consult the original paper for a deeper understanding. Additionally, we may leverage the computational formulas in this paper to implement a simple convolutional network without using hierarchical APIs.
Convolutional Neural Networks (CNN), also known as ConvNets, are widely used in many tasks such as visual image and speech recognition. After Krizhevsky et al. first applied deep convolutional networks in the 2012 ImageNet Challenge, the architecture design of deep convolutional neural networks has attracted many researchers to contribute. This has also significantly impacted the construction of deep learning architectures, such as TensorFlow, Caffe, Keras, and MXNet. Although deep learning implementations can be easily accomplished through frameworks, the mathematical theories and concepts are very difficult for beginners and practitioners to understand. This paper will attempt to outline the architecture of convolutional networks and explain the mathematical derivations involving activation functions, loss functions, forward propagation, and backward propagation. In this article, we use grayscale images as input information, ReLU and Sigmoid activation functions to construct the nonlinear properties of the convolutional network, and the cross-entropy loss function to calculate the distance between predicted values and true values. The architecture of this convolutional network includes a convolution layer, a pooling layer, and several fully connected layers.
2 Architecture
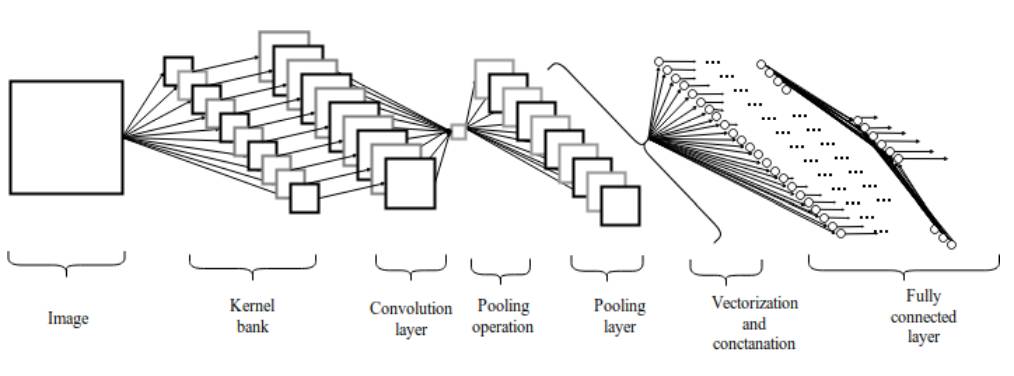
Figure 2.1: Convolutional Neural Network Architecture
2.1 Convolution Layer
The convolution layer consists of a set of parallel feature maps, formed by sliding different convolution kernels over the input image and performing certain operations. Additionally, at each sliding position, the convolution kernel performs an element-wise multiplication and summation operation with the input image to project the information within the receptive field onto an element in the feature map. This sliding process can be referred to as stride Z_s, which is a factor controlling the output feature map size. The convolution kernel is much smaller than the input image and overlaps or acts parallelly on the input image, with all elements in a feature map calculated by a single convolution kernel, meaning that a feature map shares the same weights and biases.
However, using smaller convolution kernels will lead to imperfect coverage and limit the learning algorithm’s capabilities. Therefore, we generally use zero-padding around the image or the Z_p process to control the size of the input image. Using zero-padding around the image [10] will also control the size of the feature map. During the algorithm’s training process, the dimensions of a set of convolution kernels are generally (k_1, k_2, c), and these convolution kernels slide over fixed-size input images (H, W, C). Stride and padding are important means of controlling the dimensions of the convolution layer, thus producing the feature maps that stack together to form the convolution layer. The size of the convolution layer (feature map) can be calculated using the following formula 2.1.
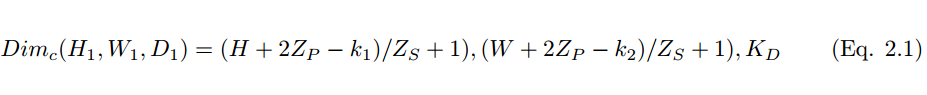
Where H_1, W_1, and D_1 represent the height, width, and depth of a feature map, respectively, Z_p is padding, and Z_s is stride size.
2.2 Activation Function
The activation function defines the output of neurons given a set of inputs. We pass the weighted sum of the linear network input values to the activation function for nonlinear transformation. Typical activation functions are based on conditional probabilities, returning 1 or 0 as output values, i.e., op {P(op = 1|ip) or P(op = 0|ip)}. When the network input information ip exceeds a threshold, the activation function returns a value of 1 and passes information to the next layer; if the network input ip value is below the threshold, it returns a value of 0 and does not pass information. Based on the separation of relevant and irrelevant information, the activation function decides whether a neuron should be activated. The higher the network input value, the greater the activation. Different types of activation functions have various applications, with some commonly used activation functions shown in Table 1.
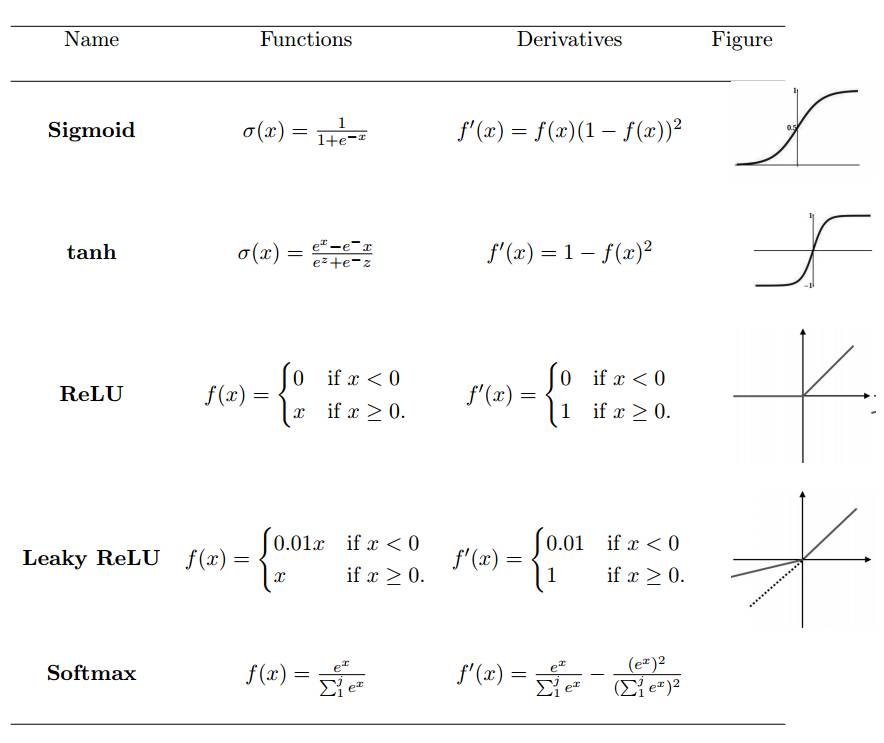
Table 1: Nonlinear Activation Functions
2.3 Pooling Layer
The pooling layer, also known as the down-sampling layer, combines the output of a cluster of neurons from the previous layer with a single neuron in the next layer. The pooling operation is performed after nonlinear activation, where the pooling layer helps reduce the number of parameters and avoid overfitting, and it can also serve as a smoothing method to eliminate unwanted noise. The most common pooling method is simple max pooling, while in some cases, we also use average pooling and L2 norm pooling operations.
When using the number of convolution kernels D_n and stride size Z_s to perform pooling operations, their dimensions can be calculated using the following formula:
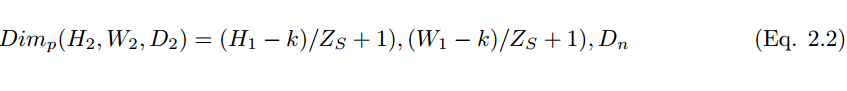
2.4 Fully Connected Layer
After the pooling layer, the three-dimensional pixel tensor needs to be converted into a single vector. These vectorized and concatenated data points are then fed into the fully connected layer for classification. The function of the fully connected layer is the weighted sum of features plus the bias term, fed to the activation function’s result. The architecture of the convolutional network is shown in Figure 2. This local connection type architecture surpasses traditional machine learning algorithms in image classification problems [11] [12].
2.5 Loss or Cost Function
The loss function maps one or more variable events to a real number related to some cost. The loss function is used to measure model performance and the inconsistency between the actual value y_i and the predicted value y hat. Model performance increases as the value of the loss function decreases.
If the output vector of all possible outputs is y_i = {0, 1} and an event x with a set of input variables x = (xi, x2, . . . xt), then the mapping from x to y_i is as follows:
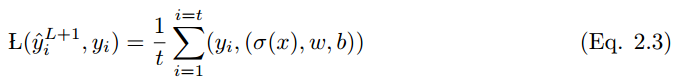
Where L(y_i hat, y_i) is the loss function. Many types of loss functions have different applications; below are some of them.
2.5.1 Mean Squared Error
The mean squared error, also known as the squared loss function, is commonly used in linear regression models to assess performance. If y_i hat is the output value of t training samples and y_i is the corresponding label value, then the mean squared error (MSE) is:
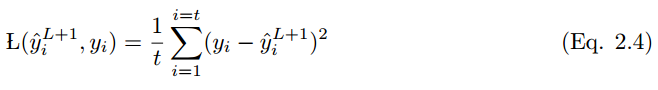
The downside of MSE is that when it occurs together with the Sigmoid activation function, it may lead to slow learning speed (slower convergence).
Other loss functions described in this section include Mean Squared Logarithmic Error, L_2 loss function, L_1 loss function, Mean Absolute Error, Mean Absolute Percentage Error, etc.
2.5.2 Cross-Entropy
The most commonly used loss function is the cross-entropy loss function, as shown below. If the output y_i has a probability in the training set label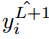 
of 
, and the output y_i does not have a probability in the training set label 
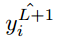of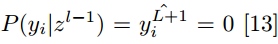 
. The expected label is y, thus:
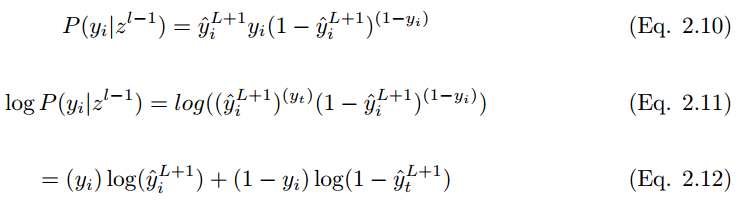
To minimize the cost function,
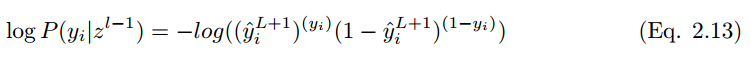
In the case of i training samples, the cost function is:
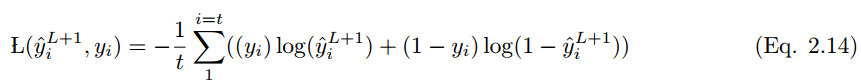
3 Learning of Convolutional Networks
3.1 Feedforward Inference Process
The feedforward propagation process of convolutional networks can be mathematically explained as multiplying the input values by randomly initialized weights, then each neuron adds an initial bias term, and finally, summing all products of all neurons to feed into the activation function, which performs a nonlinear transformation on the input values and outputs the activation results.
In discrete color space, images and convolution kernels can be represented as (H, W, C) and (k_1, k_2, c) three-dimensional tensors, where m, n, c represent the pixel at row m and column n of the c-th image channel, respectively. The first two parameters represent spatial coordinates, while the third parameter represents the color channel.
If a convolution kernel slides over a color image, the convolution operation of the multi-dimensional tensor can be represented as:
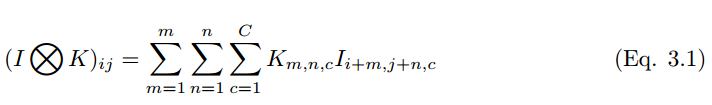
The convolution process can be denoted by the symbol ⓧ. For grayscale scalar images, the convolution process can be represented as,
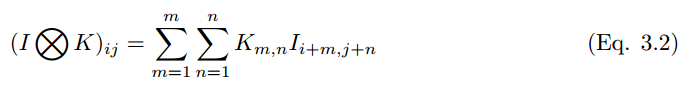
A convolution kernel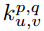 
(hereafter referred to as k_p,q|u,v) slides to the position of image I_m,n with a stride of 1 and with padding. Then, the feature map 
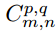(hereafter referred to as C_p,q|m,n) can be calculated as
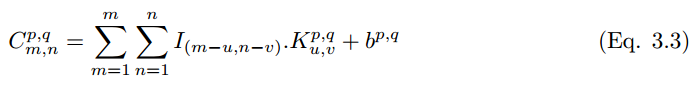
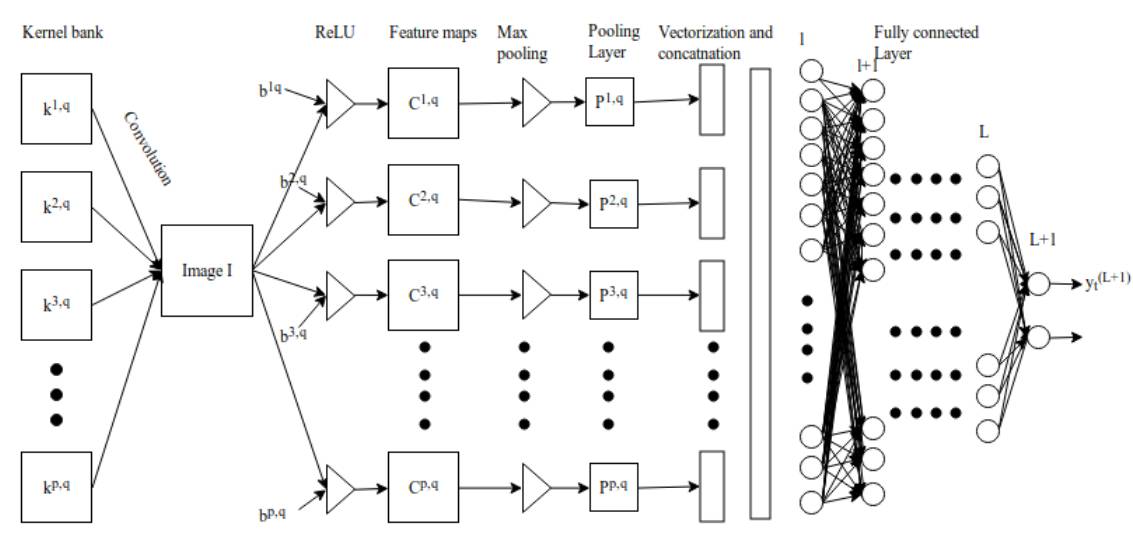
Figure 3.1: Convolutional Neural Network
After performing convolution, we need to use a nonlinear activation function to obtain the feature map:
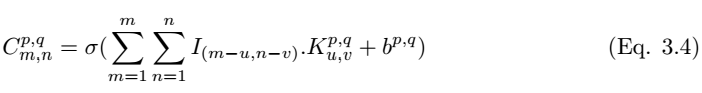
Where σ is the ReLU activation function. The pooling layer P_p,q|m,n can be constructed by selecting the maximum values from the convolution layer’s m,n, and the construction of the pooling layer can be expressed as:
The output of the pooling layer P^p,q can be concatenated into a vector of length p*q, which can then be fed into the fully connected network for classification. Subsequently, the vectorized data points from layer l-1 can be calculated using the following equation:
The long vector is fed from layer l to the L+1 layer of the fully connected network. If there are L fully connected layers and n neurons, then l can represent the first fully connected layer, L represents the last fully connected layer, and L+1 is the classification layer shown in Figure 3.2. The feedforward process in the fully connected layer can be represented as:
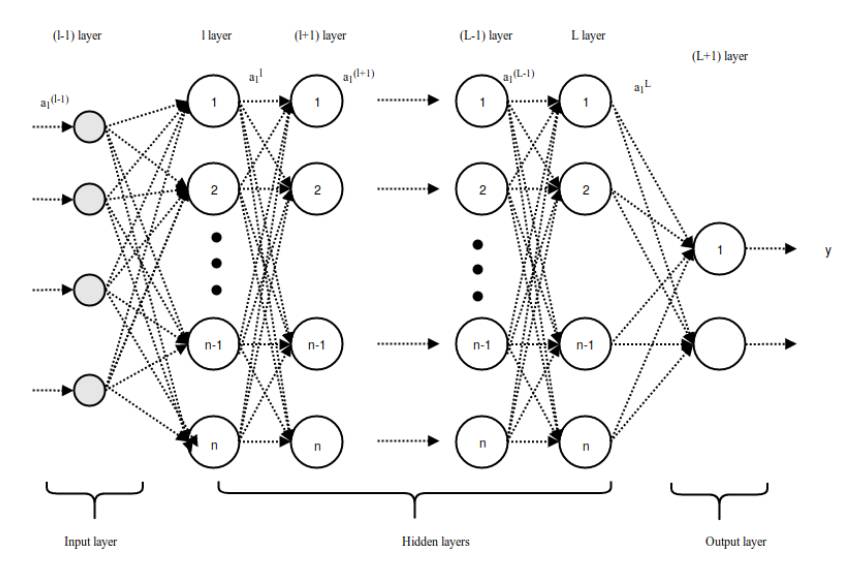
Figure 3.2: Feedforward Process in the Fully Connected Layer
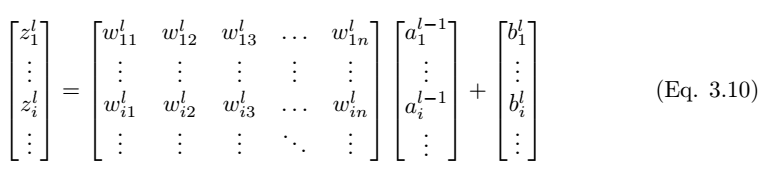
As shown in Figure 3.3, we consider a single neuron (j) in the fully connected layer l. The input values a_l-1,i are multiplied by the weights w_ij to obtain a weighted sum, and the bias term b_l,j is added. Then we feed the input value z_l,i of the last layer into the nonlinear activation function σ. The input value of the last layer can be calculated using the following equation:
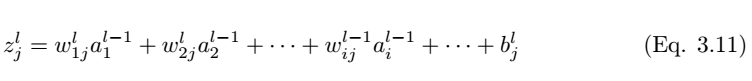
Where z_l,i is the input value of the activation function for neuron j in layer l.
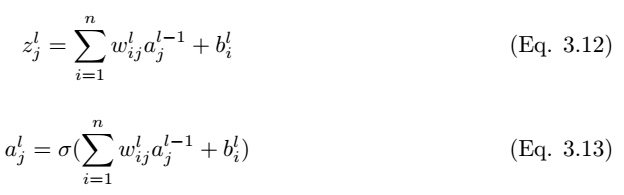
Therefore, the output of layer l is
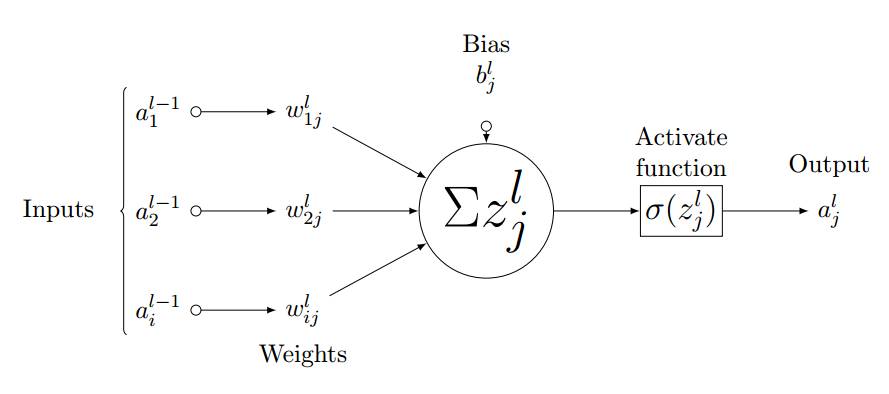
Figure 3.3: Feedforward Process for Neuron j in Layer l
Where a^l is
W^l is
Similarly, the output value of the last layer L is
Where
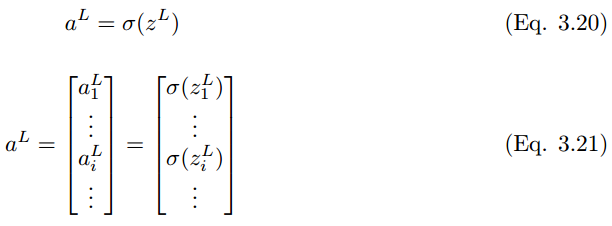
Extending these to the classification layer, the final output prediction value y_i hat for neuron unit (i) in layer L + 1 can be represented as:
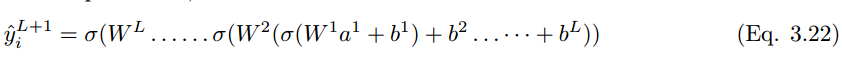
If the predicted value is y_i hat and the actual labeled value is y_i, then the model’s performance can be calculated using the following loss function equation. According to Eqn.2.14, the cross-entropy loss function is:
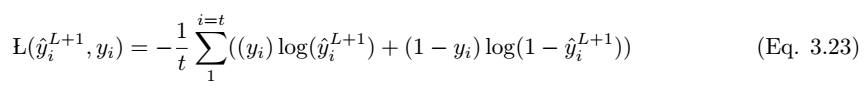
This is a brief mathematical process of forward propagation; this paper also focuses on the mathematical process of backward propagation, but due to space limitations, we will not present it in this article. Interested readers can refer to the original paper.
4 Conclusion
This article provides an overview of the architecture of convolutional neural networks, including different activation functions and loss functions, while detailing the steps of feedforward and backward propagation. For mathematical simplicity, we use grayscale images as input information. The stride value of the convolution kernel is set to 1, using padding. The nonlinear transformations of the intermediate and final layers are accomplished through ReLU and sigmoid activation functions. The cross-entropy loss function is used to measure model performance. However, a significant amount of optimization and regularization steps are needed to minimize the loss function, increase the learning rate, and avoid model overfitting. This paper attempts to consider only the formulation of a typical convolutional neural network architecture with gradient descent optimization.
Those destined to meet will eventually come together; Mu Ke Jun thought that if he didn’t share it, we might miss each other~
“Reservation, Experience – New Dimension Space Station”
“【Member Recruitment】‘New Dimension Space Station’ 100 events in a year waiting for you to join”
“Those destined to meet will always come together – MOOC public account recruiting long-term collaborators”
“【Survey】‘In the Screen Age, the Relationship Between Visual Area and Learning Efficiency’ – Did you see it right?”