Natural Language Processing
Author: Machine Learning Beginner
Original Author: Jalammar, Translated by Huang Haiguang
Since 2013, word2vec has been an effective method for word embedding. This article presents word2vec in an illustrated manner, with no mathematical formulas, making it very easy to understand, and is recommended for beginners to read.
(Original Author: jalammar, Translation: Huang Haiguang).
Note: This is another version of the translation; there are other versions available online, all independently completed..
Original link:
https://jalammar.github.io/illustrated-word2vec/
The code for this article has been uploaded to our GitHub:
https://github.com/fengdu78/machine_learning_beginner/tree/master/word2vec
The Main Text Begins
I find the concept of embeddings to be one of the most fascinating ideas in machine learning. If you have ever used Siri, Google Assistant, Alexa, Google Translate, or even the next-word prediction feature on your smartphone keyboard, you have likely benefited from this idea, which has become central to natural language processing models. In recent decades, there has been significant development in using embedding techniques for neural models (recent advancements include contextual embeddings in cutting-edge models like BERT and GPT-2).
Since 2013, word2vec has been an effective method for creating word embeddings. Beyond the method of word embedding, some of its concepts have proven to be effective in creating recommendation engines and understanding sequential data in non-linguistic tasks. Companies like Airbnb, Alibaba, Spotify, and Anghami have taken this excellent tool from the NLP world and applied it in production, thus supporting new types of recommendation engines.
We will discuss the concept of embeddings and the mechanism for generating embeddings using word2vec.
Let’s start with an example to understand how vectors can represent things.
Did you know that a list of five numbers (vectors) can represent your personality?
Personality Embedding: How is your personality?
Using a range of 0 to 100 to represent your personality (where 0 is the most introverted and 100 is the most extroverted).
The Big Five personality traits test asks you a list of questions and then scores you on many aspects, introversion/extroversion being one of them.
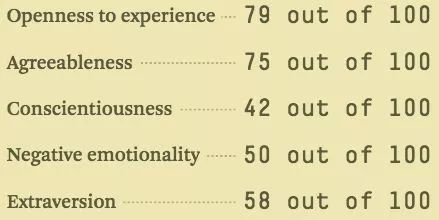
Figure: Example of test results. It can tell you a lot about yourself and has predictive power in academic, personal, and professional success.
Assuming my test score is 38/100. We can plot it this way:

Let’s switch the range to -1 to 1:

Understanding a person, one dimension of information is not enough, so let’s add another dimension – the score of another feature in the test.
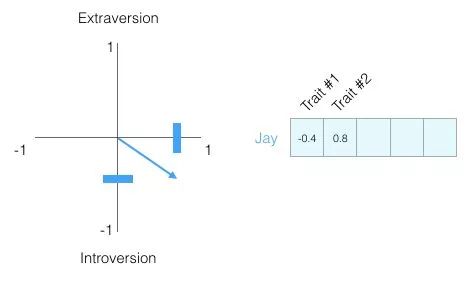
You might not know what each dimension represents, but you can still gain a lot of useful information from a person’s vector representation of personality.
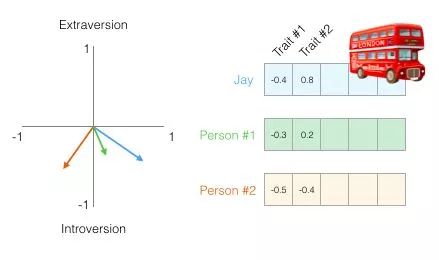
We can now say that this vector partially represents my personality. The usefulness of vector representation appears when you want to compare two other people with me. In the following image, which of the two people is more like me?
When processing vectors, a common method for calculating similarity scores is cosine similarity:

Person One has a high cosine similarity score with me, so our personalities are quite similar.
However, two dimensions are still not enough to capture sufficient information about different populations. Decades of psychological research have studied five main traits (and a large number of sub-traits). So we use all five dimensions in the comparison:
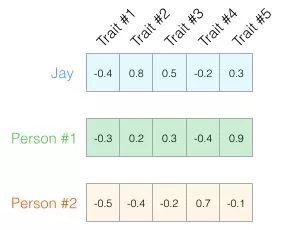 We cannot plot five dimensions in two dimensions, which is a common challenge in machine learning; we often need to think in higher-dimensional spaces. But the good news is that cosine similarity still works. It applies to any number of dimensions:
We cannot plot five dimensions in two dimensions, which is a common challenge in machine learning; we often need to think in higher-dimensional spaces. But the good news is that cosine similarity still works. It applies to any number of dimensions: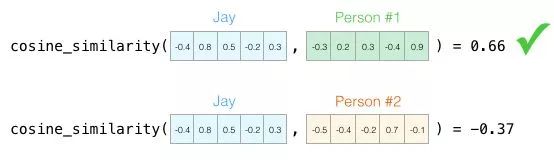
Two central ideas of embeddings:
-
We can represent people (things) as vectors of numbers.
-
We can easily compute the relationships between similar vectors.

Word Embedding
We import GloVe vectors trained on Wikipedia:
import gensim
import gensim.downloader as api
model = api.load('glove-wiki-gigaword-50')model["king"]
# View the most similar words to "king"[('prince', 0.8236179351806641),
('queen', 0.7839042544364929),
('ii', 0.7746230363845825),
('emperor', 0.7736247181892395),
('son', 0.766719400882721),
('uncle', 0.7627150416374207),
('kingdom', 0.7542160749435425),
('throne', 0.7539913654327393),
('brother', 0.7492411136627197),
('ruler', 0.7434253096580505)]This is a list of 50 numbers, and we cannot clearly say what the values represent. We put all these numbers in a row so that we can compare them with other word vectors. Let’s color-code the cells based on their values (red if close to 2, white if close to 0, blue if close to -2)
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
plt.figure(figsize=(15, 1))
sns.heatmap([model["king"]],
xticklabels=False,
yticklabels=False,
cbar=False,
vmin=-2,
vmax=2,
linewidths=0.7)
plt.show()
We will ignore the numbers and only look at the colors to indicate the values of the cells, comparing “King” with other words:
plt.figure(figsize=(15, 4))
sns.heatmap([
model["king"],
model["man"],
model["woman"],
model["king"] - model["man"] + model["woman"],
model["queen"],
],
cbar=True,
xticklabels=False,
yticklabels=False,
linewidths=1)
plt.show()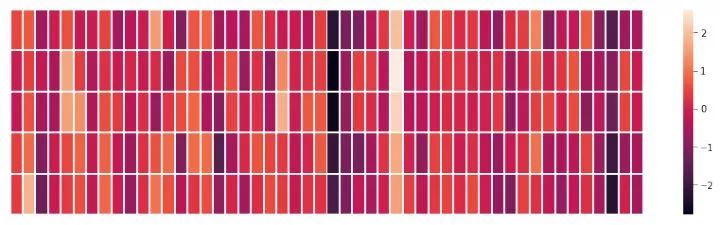
Notice how “man” and “woman” are more similar to each other than either is to “king”? This tells you something. These vector representations capture the information/meaning/associations of these words.
This is another example list (by scanning columns vertically to find columns with similar colors):
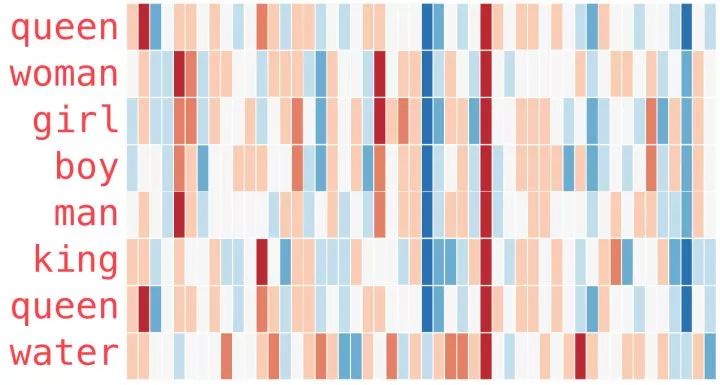
There are a few points to note:
-
All these different words have a straight red column. They are similar in this dimension (we don’t know what each dimension code represents).
-
You can see how “woman” and “girl” are similar in many places, just like “man” and “boy”.
-
“Boy” and “girl” also have similarities with each other but differ from “woman” or “man”. Could these be a fuzzy concept of youth? Possibly.
-
All words except the last one represent people. I added an object “water” to show the differences between categories. For example, you can see the blue column goes down and stops before embedding “water”.
-
There is an obvious place where “king” and “queen” are similar to each other and different from all others. Analogy.
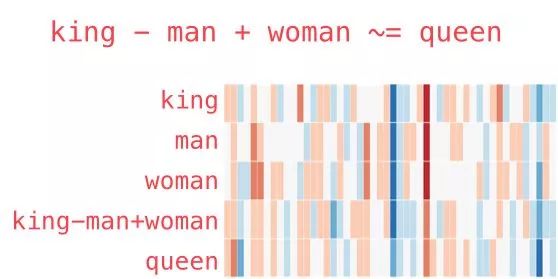
We can add and subtract word embeddings and get interesting results, the most famous example being the formula: “king” – “man” + “woman”:
model.most_similar(positive=["king","woman"],negative=["man"])[('queen', 0.8523603677749634),
('throne', 0.7664334177970886),
('prince', 0.759214460849762),
('daughter', 0.7473883032798767),
('elizabeth', 0.7460220456123352),
('princess', 0.7424569725990295),
('kingdom', 0.7337411642074585),
('monarch', 0.7214490175247192),
('eldest', 0.7184861898422241),
('widow', 0.7099430561065674)]We can visualize this analogy as before:
Language Modeling
If we want to give an example of an NLP application, one of the best examples would be the next word prediction feature on smartphone keyboards. This is a feature used hundreds of times daily by billions of people.
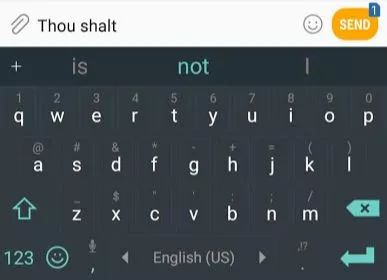
The next word prediction is a task that can be solved by language models. A language model can take a list of words (say two words) and try to predict the word that comes after them.
In the screenshot above, we can think of the model as accepting these two green words (thou shalt) and returning a list of suggestions (with “not” being the word with the highest probability):

We can imagine the model as this black box:

But in reality, the model does not output just one word. It actually outputs probability scores for all the words it knows (the model’s “vocabulary,” which can range from a few thousand to over a million words). Then the application must find the word with the highest score and present it to the user.
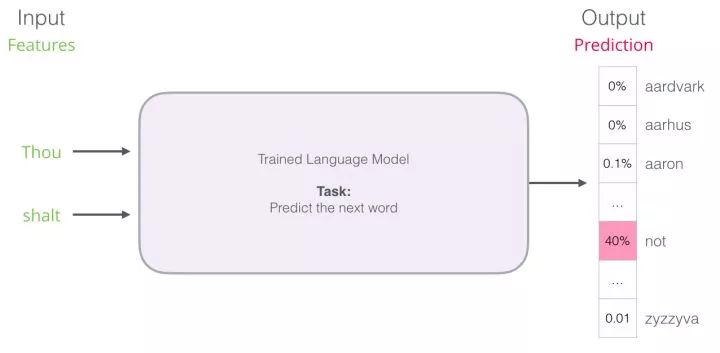
Figure: The output of a neural language model is the probability scores of all the words the model knows. Here we refer to probabilities as percentages; for example, a probability of 40% would be represented as 0.4 in the output vector.
After training, early neural language models (Bengio 2003) calculated predictions in three steps:
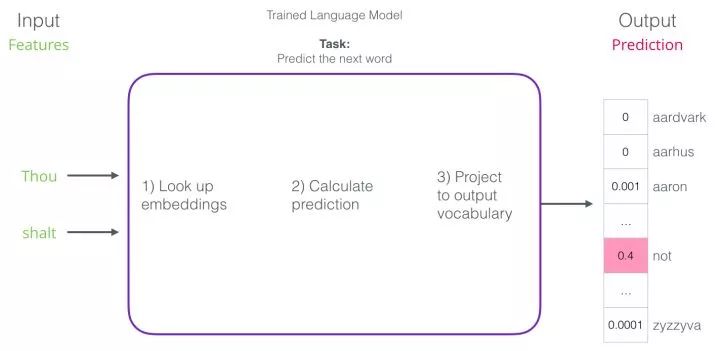
When discussing embeddings, the first step is the most relevant for us. One of the outcomes of the training process is this matrix that contains the embeddings for each word in our vocabulary. During prediction time, we simply look up the embeddings for the input words and use them to compute predictions:
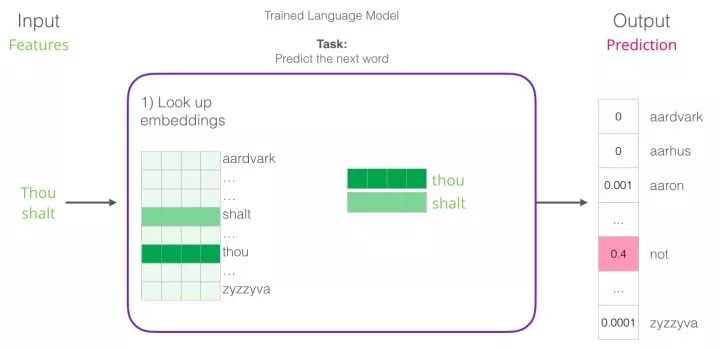
Now let’s turn to the training process to understand how the embedding matrix works.
Training Language Models
Compared to most other machine learning models, language models have a huge advantage. That is: All of our books, articles, Wikipedia content, and other forms of large text data can serve as training data. In contrast, many other machine learning models require manually designed features and specially collected data. Words are embedded by looking at the words that often appear next to them. This is how the mechanism works:
-
We obtain a large amount of text data (for example, all Wikipedia articles). Then
-
We have a window (say three words) that we slide over all the text.
-
The sliding window generates training samples for our model.
As this window slides over the text, we (virtually) generate a dataset for training the model. To accurately see how this is done, let’s look at how the sliding window processes this phrase:
When we start, the window is on the first three words of the sentence:

We take the first two words as features and the third word as the label:

We have now generated the first sample in the dataset that we can later use to train the language model.
Then we slide the window to the next position and create the second sample:
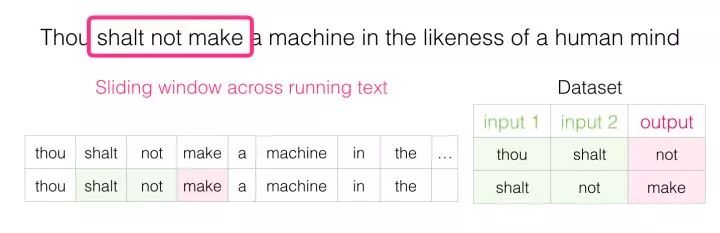
Now we generate the second example.
Before long, we will have a larger dataset with different pairs of words appearing:

In practice, the model often trains as we slide the window. But I find it clearer logically to separate the “dataset generation” phase from the training phase. Besides neural network-based language modeling approaches, a technique called N-gram is commonly used to train language models.
To understand how this transition from N-gram to neural models reflects real-world products, I recommend reading this 2015 blog post that introduces their neural language model and compares it to previous N-gram models.
Looking Both Ways
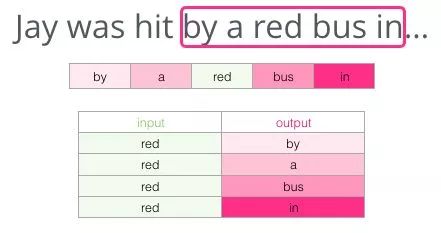
Given the content before the sentence, fill in the blanks:

The background I give you here is the five words before the blank (and the previously mentioned “bus”). I believe most people would guess that the word in the blank would be “bus.” But if I give you another piece of information: the sentence after the blank, would that change your answer?

This completely changes what should be left in the blank. The word “red” is now the most likely to fill in the blank. What we learn from this is that the words before and after specific words have informational value. It turns out that considering both directions (the words to the left and right of the word we are guessing) allows word embeddings to perform better.
Let’s see how we can adjust the way we train our model to address this issue.
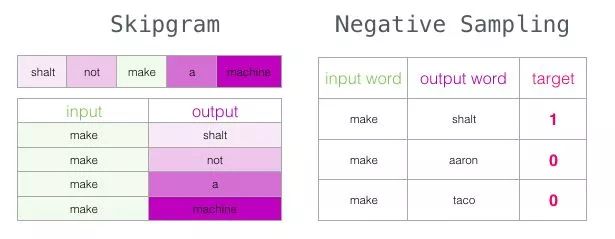
Skipgram
We can look not only at the two words before the target word but also at the two words after it.

If we do this, the dataset we actually construct and train the model on will look like this:
 This is referred to as the continuous bag-of-words structure, described in one of the word2vec papers.
This is referred to as the continuous bag-of-words structure, described in one of the word2vec papers.Another structure is slightly different from the continuous bag-of-words structure but can also yield good results. This structure attempts to use the current word to guess the neighboring words rather than guessing a word based on its context (the words before and after it). We can visualize it sliding over the training text as follows:

This method is called the skipgram architecture. We can visualize the sliding window as follows:

This adds these four samples to our training dataset:
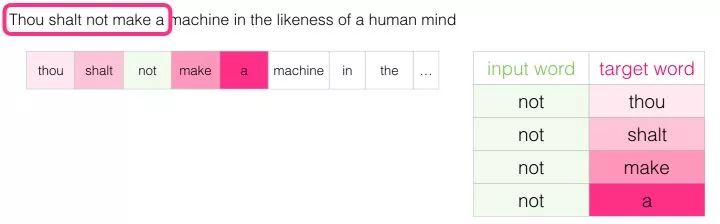
Then we slide the window to the next position:
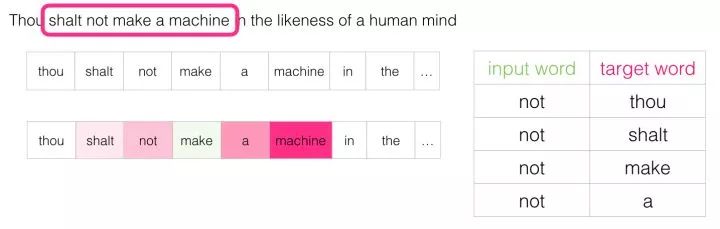
This will produce our next four samples:
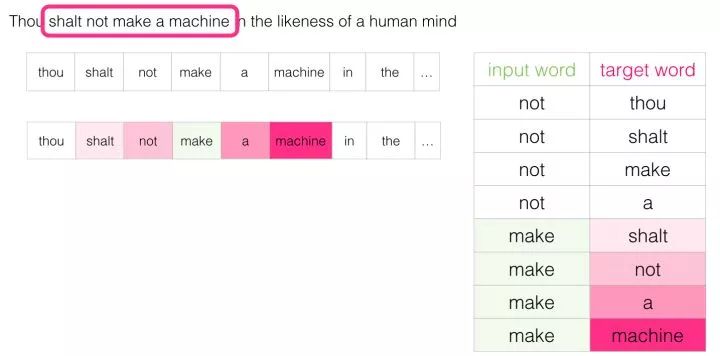
After sliding a few positions, we have more samples:
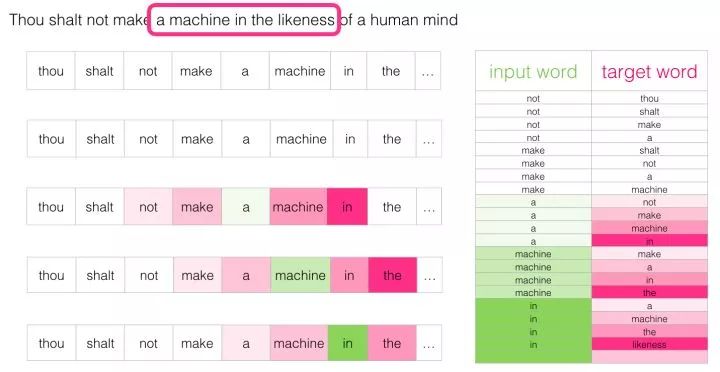
Revisiting the Training Process
Now that we have extracted our skipgram training dataset from the existing running text, let’s see how we use it to train a basic neural language model that predicts neighboring words.
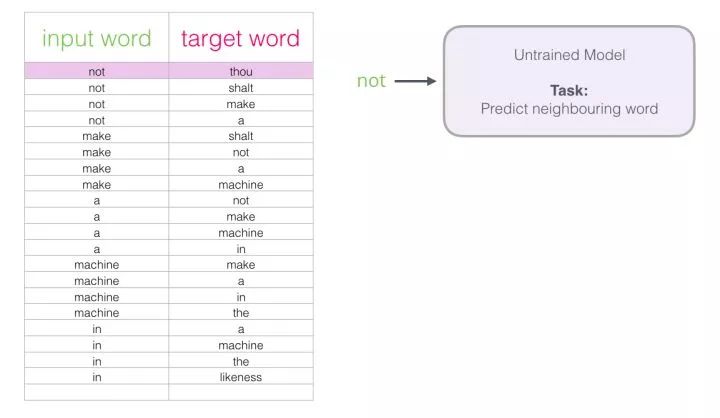
We start with the first sample in the dataset. We provide the features to the untrained model and ask it to predict an appropriate neighboring word.
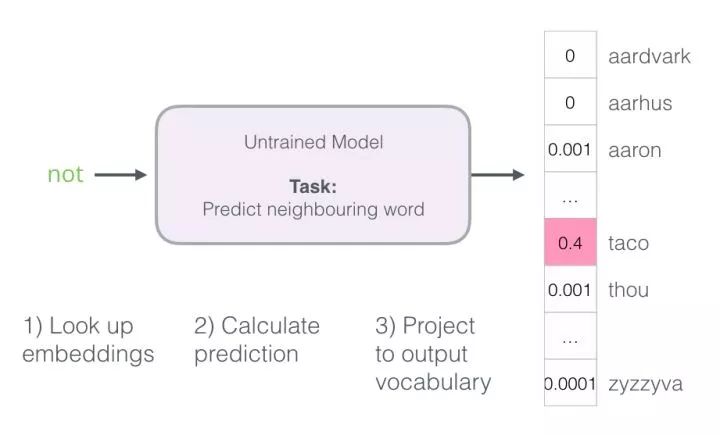
The model performs three steps and outputs a prediction vector (a probability distribution across its vocabulary). Since the model is untrained, the predictions at this stage are likely incorrect. But that’s okay. We know what word it should guess: the label/output cell in the row we are currently using to train the model:
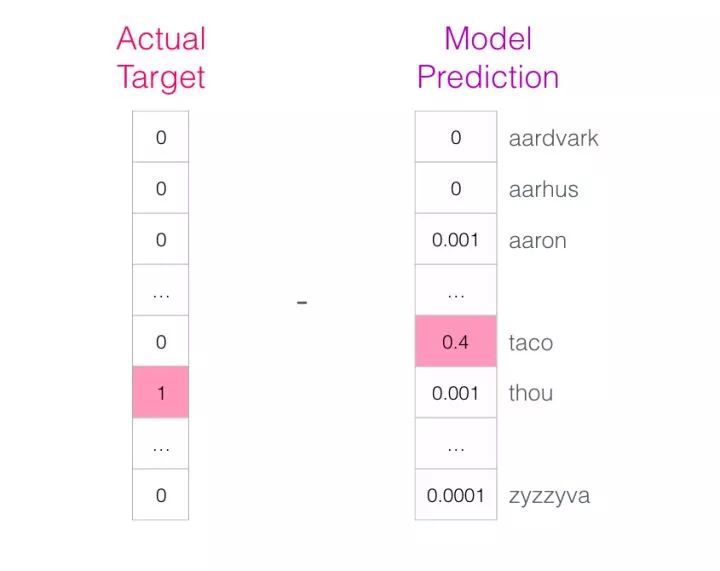
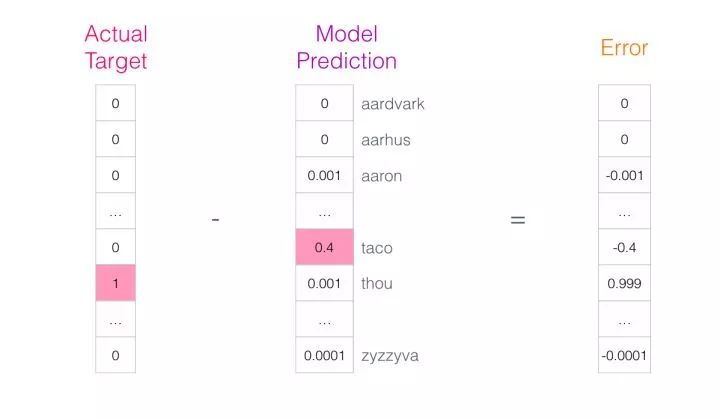
This error vector can now be used to update the model so that the next time “not” is input, the model is more likely to guess “thou.”
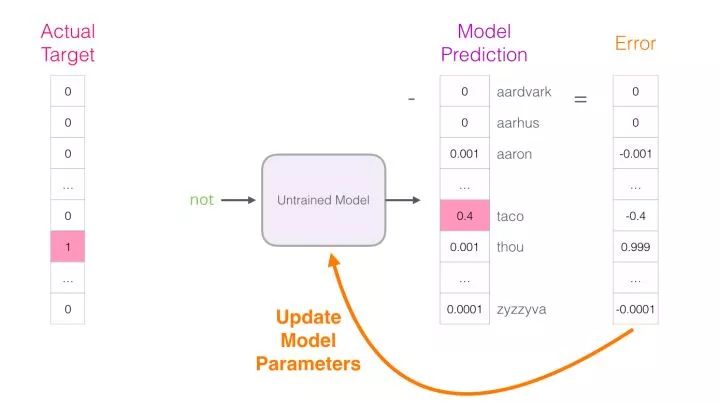
This is the first step of training. We continue with the next sample in the dataset and perform the same process, then the next sample, until we have covered all samples in the dataset. This concludes one epoch of training. We continue training for multiple epochs, and then we have a trained model from which we can extract the embedding matrix for any other applications.
While this deepens our understanding of the process, it still does not represent the actual training process of word2vec.
Negative Sampling
Recall how this neural language model calculates its predictions in three steps:
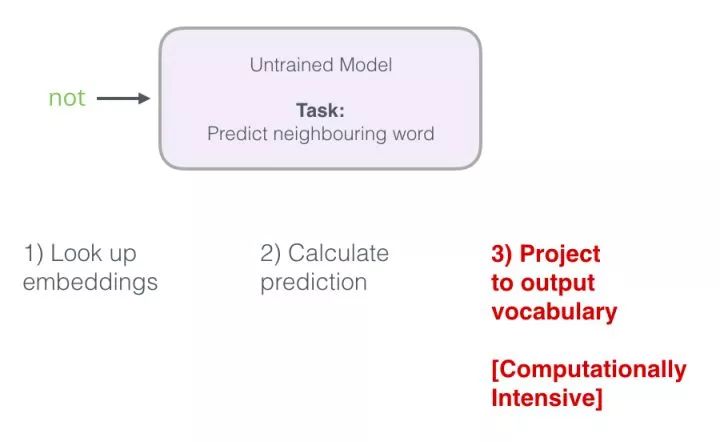
From a computational standpoint, the third step is very resource-intensive: especially since we will do this for each training sample (likely tens of millions of times). We need to do something to improve efficiency. One way is to split the target into two steps:
-
Generate high-quality word embeddings (don’t worry about predicting the next word).
-
Use these high-quality embeddings to train the language model (to predict the next word).
We will focus on step 1 because we are concentrating on embeddings. To generate high-quality embeddings using a high-performance model, we can switch the task of predicting neighboring words:
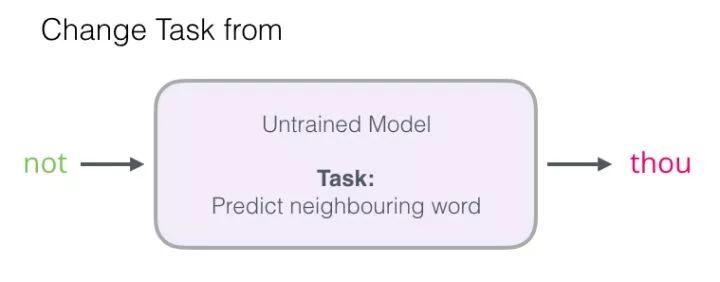
And switch it to a model that takes input and output words and produces a score indicating whether they are neighbors (0 means “not neighbors,” 1 means “neighbors”).
 This simple change transforms the model we need from a neural network to a logistic regression model: thus making it simpler and faster to compute.
This simple change transforms the model we need from a neural network to a logistic regression model: thus making it simpler and faster to compute.
This change requires us to switch the structure of the dataset – the labels are now a new column with a value of 0 or 1. They will all be 1 because all the words we added are neighbors.
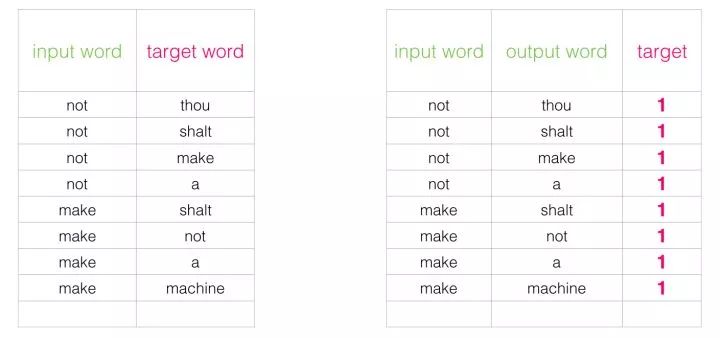
This can be computed at lightning speed – processing millions of examples in minutes. But we need to close one loophole. If all our examples are positive (target: 1), we open the possibility of our smart model always returning 1 – achieving 100% accuracy but learning nothing and generating garbage embeddings.
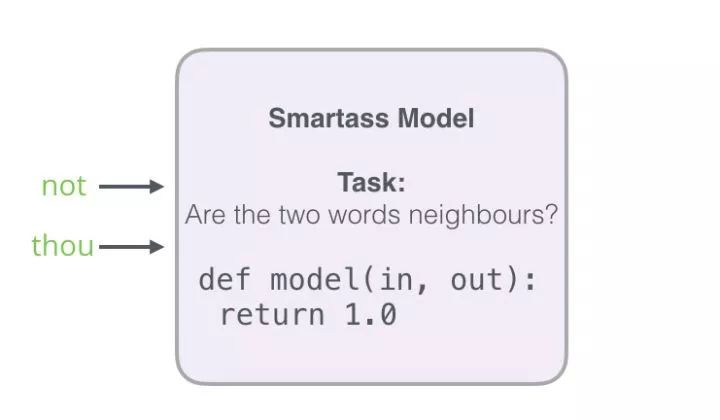
To solve this problem, we need to introduce negative samples into the dataset – samples of words that are not neighbors. Our model needs to return 0 for these samples. Now this is a challenge, and the model must work hard to solve it, and it must still be fast.

Figure: For each sample in our dataset, we added negative samples. They have the same input word and a 0 label. But what do we fill in as the output word? We randomly sample words from the vocabulary.

The inspiration for this idea comes from Noise-contrastive estimation. We contrast the actual signal (the positive examples of neighboring words) with noise (the randomly chosen non-neighboring words). This is a huge trade-off in computational and statistical efficiency.
Skipgram with Negative Sampling (SGNS)
We have now introduced two core ideas in word2vec: negative sampling and skipgram.
Word2vec Training Process
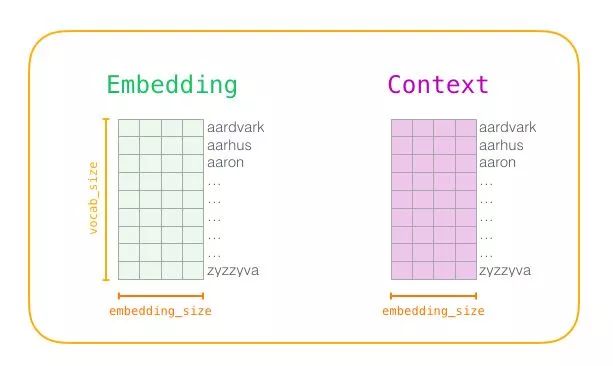
Now that we have established the two core ideas of skipgram and negative sampling, we can continue to examine the actual training process of word2vec in detail. Before the training process begins, we preprocess the text that we are training the model on. In this step, we determine the size of the vocabulary (let’s call it <span>vocab_size</span>, say, consider it as 10,000) and which words belong to it. At the beginning of the training phase, we create two matrices – the <span>Embedding</span> matrix and the <span>Context</span> matrix. These two matrices embed each word in our vocabulary (the <span>vocab_size</span> is one of their dimensions). The second dimension is the length of the embedding we want each time (<span>embedding_size</span> – 300 is a common value, but the example earlier in this article is 50).
At the beginning of the training process, we initialize these matrices with random values. Then we start the training process. In each training step, we take a positive sample and its associated negative samples. Let’s look at our first set:
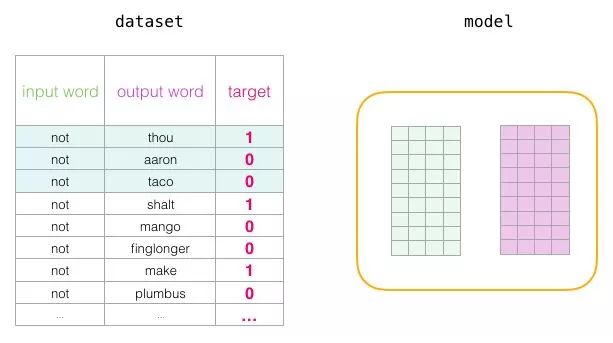
Now we have four words: the input word <span>not</span> and the output/context words: (<span>thou</span> the actual neighbor), <span>aaron</span>, and <span>taco</span> (negative samples). We continue to look for their embeddings – for the input word, we look at the <span>Embedding</span> matrix. For the context words, we look at the <span>Context</span> matrix (even though both matrices embed each word in our vocabulary).
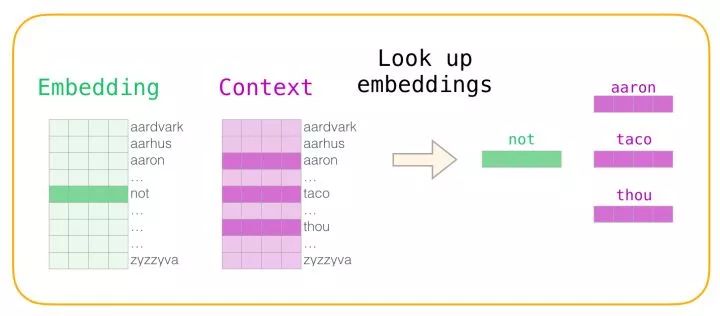
Then we compute the dot product of the input embedding with each context embedding. In each case, a number is produced that indicates the similarity between the input and context embeddings.
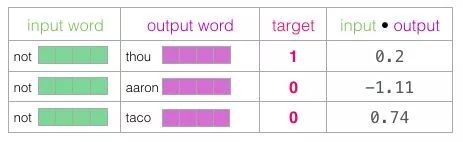
Now we need a way to transform these scores into something that looks like probabilities: using the sigmoid function to convert probabilities to 0 and 1.
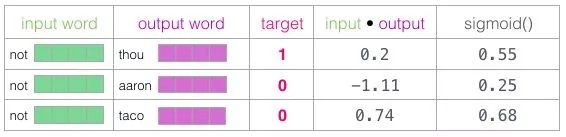
Now we can view the output of the sigmoid operation as the model output for these samples. You can see that <span>taco</span> scores higher than <span>aaron</span>, and still has the lowest score before and after the sigmoid operation. Since the untrained model has made a prediction and we have an actual target label to compare, let’s calculate the error in the model’s prediction. To do this, we simply subtract the sigmoid scores from the target label.
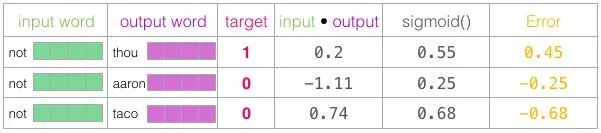
This is the “learning” part of “machine learning.” Now we can use this error score to adjust the embeddings of <span>not</span>, <span>thou</span>, <span>aaron</span>, and <span>taco</span>, so that the next time we perform this calculation, the result will be closer to the target score.
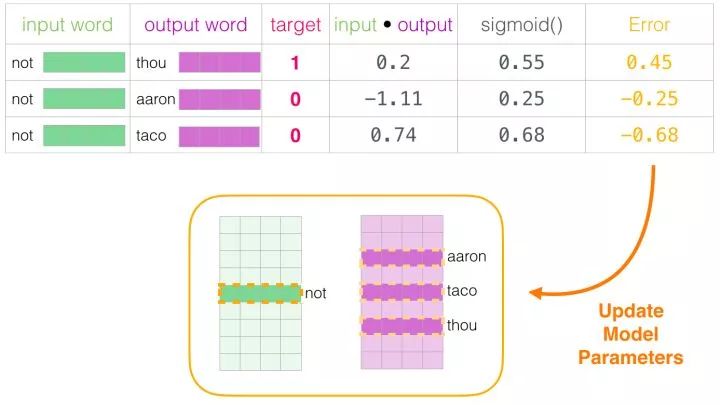
The training step ends here. We obtain slightly better embeddings from this step (<span>not</span>, <span>thou</span>, <span>aaron</span>, and <span>taco</span>). We now proceed to the next step (the next positive sample and its related negative samples) and perform the same process again.
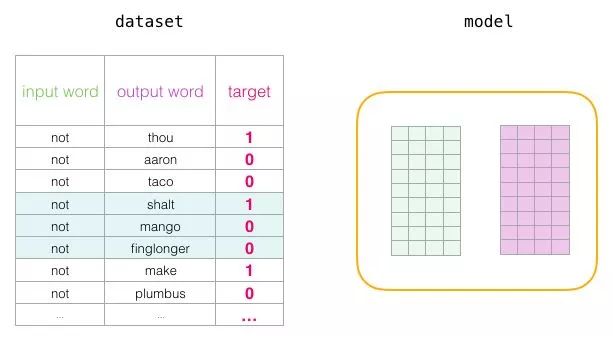
As we loop through the entire dataset multiple times, the embeddings continue to improve. Then we can stop the training process, discard the <span>Context</span> matrix, and use the <span>Embeddings</span> matrix as pre-trained embeddings for the next task.
The Window Size and Number of Negative Samples
Two key hyperparameters in the word2vec training process are the window size and the number of negative samples.
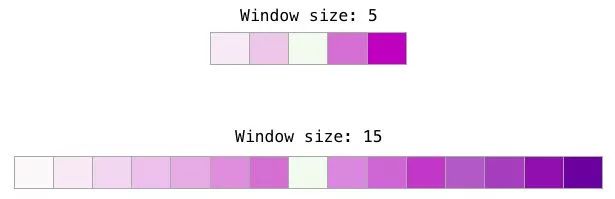
Different window sizes can better serve different tasks. A heuristic approach is to use smaller window embeddings (2-15), where a high similarity score between two embeddings indicates that these words are interchangeable (note that if we only look at surrounding words, antonyms can often be interchangeable – for example, good and bad often appear in similar contexts). Using larger window embeddings (15-50 or even more) results in embeddings where similarity is more indicative of word relevance. In reality, you often need to provide annotated guidance to the embedding process to bring useful similarity to your task. Gensim defaults to a window size of 5 (the input word itself plus the two words before and the two words after the input word).
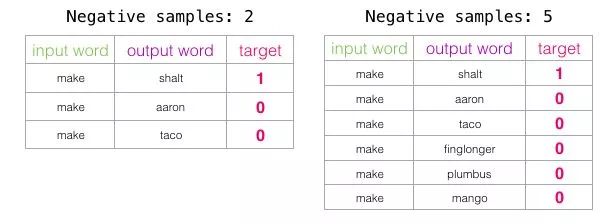
The number of negative samples is another factor in the training process. The original paper indicated a number of negative samples between 5-20. It also noted that when you have a sufficiently large dataset, 2-5 seems to be enough. Gensim defaults to 5 negative samples.
Conclusion I hope you now have a better understanding of word embeddings and the word2vec algorithm. I also hope that now when you read a paper that mentions “skip gram with negative sampling” (SGNS), you will have a better grasp of these concepts. Article Author: jalammar.
References and Further Reading
-
Distributed Representations of Words and Phrases and their Compositionality [pdf]
-
Efficient Estimation of Word Representations in Vector Space [pdf]
-
A Neural Probabilistic Language Model [pdf]
-
Speech and Language Processing by Dan Jurafsky and James H. Martin is a leading resource for NLP. Word2vec is tackled in Chapter 6.
-
Neural Network Methods in Natural Language Processing by Yoav Goldberg is a great read for neural NLP topics.
-
Chris McCormick has written some great blog posts about Word2vec. He also just released The Inner Workings of word2vec, an E-book focused on the internals of word2vec.
-
Want to read the code? Here are two options:
-
Gensim’s python implementation of word2vec
-
Mikolov’s original implementation in C – better yet, this version with detailed comments from Chris McCormick.
-
Evaluating distributional models of compositional semantics
-
On word embeddings, part 2
-
Dune