©PaperWeekly Original · Author|Su Jianlin
Unit|Zhuiyi Technology
Research Direction|NLP, Neural Networks

“Profit and loss problems”, “age problems”, “planting trees problems”, “cows eating grass problems”, “profit problems”… Have you ever been tormented by various types of math word problems during elementary school? No worries, machine learning models can help us solve these problems now. Let’s see how well they can perform!
This article will provide a baseline for solving elementary math word problems based on the ape210k dataset [1]. We will use a Seq2Seq model to directly generate executable mathematical expressions. The final large version of the model can achieve an accuracy of 73%+, which is higher than the results reported in the ape210k paper.

Data Processing
First, let’s take a look at the ape210k dataset:
{
"id": "254761",
"segmented_text": "Xiao Wang wants to dilute 150 kilograms of pesticide with a drug content of 20% to a solution with a drug content of 5%. How much water needs to be added in kilograms?",
"original_text": "小王要将150千克含药量20%的农药稀释成含药量5%的药水.需要加水多少千克?",
"ans": "450",
"equation": "x=150*20%/5%-150"
}
{
"id": "325488",
"segmented_text": "A circular flower bed has a radius of 4 meters. Now, we want to expand the flower bed by increasing the radius by 1 meter. How much has the area increased?",
"original_text": "一个圆形花坛的半径是4米,现在要扩建花坛,将半径增加1米,这时花坛的占地面积增加了多少米**2.",
"ans": "28.26",
"equation": "x=(3.14*(4+1)**2)-(3.14*4**2)"
}However, we need to do some preprocessing because the equation provided by ape210k is not always directly evaluable. For example, the expression 150*20%/5%-150 is an illegal expression in Python. The processing I did is as follows:
-
For percentages like a%, uniformly replace with (a/100); -
For mixed fractions like a(b/c), uniformly replace with (a+b/c); -
For true fractions like (a/b), remove parentheses in the problem to become a/b; -
For ratios represented by colons :, uniformly replace with /.
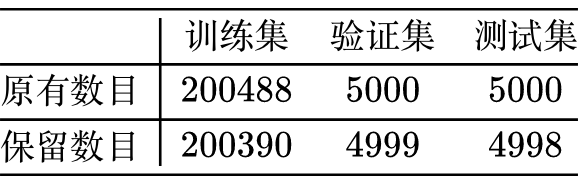

Model Overview
The model is quite straightforward; it takes original_text as input and equation as output, based on the “BERT+UniLM” architecture, training a Seq2Seq model. If you have any doubts about the model, please read “From Language Models to Seq2Seq: Transformer is Like a Play, All Rely on Mask”.
Cloud Link:
https://pan.baidu.com/s/1Xp_ttsxwLMFDiTPqmRABhg
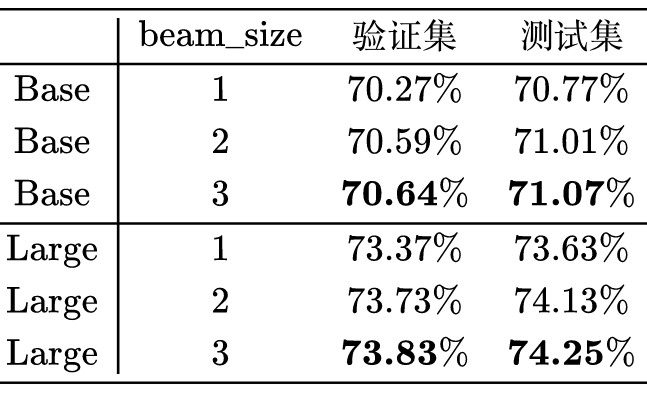
The results of the Large model are significantly higher than the 70.20% reported in the ape210k paper Ape210K: A Large-Scale and Template-Rich Dataset of Math Word Problems [4], indicating that our model here is a reasonably good baseline.

Standard Output
From a modeling perspective, our task is already complete; the model only needs to output the expression, and during evaluation, we only need to determine whether the result of evaluating the expression matches the reference answer.
However, from a practical perspective, we also need to further standardize the output based on different problems, which means we need to: 1) decide when to output what format; 2) convert the result according to the specified format.
The first step is relatively simple; generally, we can determine this based on some keywords in the problem or equation. For example, if the expression contains decimals, the output result is usually also a decimal; if the problem asks “how many vehicles”, “how many items”, “how many people”, etc., the output will be integers; if it directly asks “what fraction” or “what percentage”, then the corresponding output will be a fraction or percentage.
The more challenging part is for rounding problems, such as “each cake costs 7.90 yuan, how many cakes can be bought for 50 yuan at most?” which requires us to round down 50/7.90, but sometimes it requires rounding up. However, I was surprised to find that there are no rounding problems in ape210k, so this issue does not exist. If we encounter a dataset with rounding problems and the rule-based judgment is complicated, the most direct method is to include the rounding symbol in the equation for the model to predict.
The second step seems a bit complicated, mainly in the scenario of fractions. General readers may not know how to keep the fraction result of the expression. If we directly eval(‘(1+2)/4’, we get 0.75 (Python3), but sometimes we want the result to be the fraction 3/4.
In fact, keeping the fraction calculation falls under the category of CAS (Computer Algebra System), which essentially means symbolic computation rather than numerical computation, and Python happens to have such a tool, which is SymPy [5]. By using SymPy, we can achieve our goal. Please see the example below:
from sympy import Integer
import re
r = (Integer(1) + Integer(2)) / Integer(4)
print(r) # Output is 3/4 instead of 0.75
equation = '(1+2)/4'
print(eval(equation)) # Output is 0.75
new_equation = re.sub('(\d+)', 'Integer(\1)', equation)
print(new_equation) # Output is (Integer(1)+Integer(2))/Integer(4)
print(eval(new_equation)) # Output is 3/4

Article Summary
This article introduces a baseline for using the Seq2Seq model to solve math word problems, primarily by using “BERT+UniLM” to directly convert the questions into evaluable expressions, and shares some experiences in result standardization. Through the BERT Large model’s UniLM, we achieved an accuracy of 73%+, surpassing the results of the original paper.
References
More Reading




#Submission Channel#
Let your paper be seen by more people
How can more quality content reach readers in a shorter path and reduce the cost for readers to find quality content? The answer is: people you do not know.
There are always some people you do not know who know what you want to know. PaperWeekly may become a bridge, facilitating the collision of scholars and academic inspiration from different backgrounds and directions, generating more possibilities.
PaperWeekly encourages university laboratories or individuals to share various quality content on our platform, which can be latest paper interpretations, learning insights, or technical insights. Our only goal is to make knowledge truly flow.
📝 Submission Standards:
• The submission must be an original work, and the author must provide personal information (name + school/work unit + degree/position + research direction)
• If the article has been published elsewhere, please remind us during submission and include all published links
• PaperWeekly assumes every article is a first publication and will add an “original” label
📬 Submission Email:
• Submission Email:[email protected]
• Please send all article images separately in an attachment
• Please leave immediate contact information (WeChat or mobile phone) so we can communicate with authors during editing and publishing
🔍
Now, you can also find us on “Zhihu”
Go to the Zhihu homepage and search for “PaperWeekly”
Click “Follow” to subscribe to our column
About PaperWeekly
PaperWeekly is an academic platform for recommending, interpreting, discussing, and reporting the latest AI research papers. If you study or work in the AI field, feel free to click “Discussion Group” in the WeChat public account backend, and our assistant will take you into the PaperWeekly discussion group.


