Artificial intelligence is flourishing today; large models dominate with scale, while small models win with data.

Of course, we hope to achieve the same results with fewer resources.

A long time ago, Google conducted related research exploring how to allocate model parameter counts and training data amounts under fixed computational power to achieve the best performance.

Recently, a work involving LeCun has shown us from another angle just how flexible neural networks are in practice.

Paper link: https://arxiv.org/pdf/2406.11463

This flexibility refers to the ability of neural networks to fit training data (sample size) and what factors in practical applications influence this.

For example, the first thing we might think of is the model’s parameter count.

It is widely believed that neural networks can fit at least as many training samples as their own parameters.

This is similar to solving a system of linear equations, where the number of parameters (or equations) determines the number of solutions.

However, neural networks are actually much more complex. Although they can theoretically perform universal function approximation, in practice, the capacity of the models we train is limited, and different optimizers can lead to different results.

Therefore, this article decides to use experimental methods to examine the properties of the data itself, model architecture, size, optimizers, and regularizers.

The model’s ability to fit data (or learn information) is represented by effective model complexity (EMC).

How is this EMC calculated?

Initially, the model is trained on a small number of samples. If it achieves 100% training accuracy after training, the model is reinitialized, and the number of training samples is increased.

This process is iteratively executed, gradually increasing the sample size until the model no longer perfectly fits all training samples, taking the maximum sample size that the model can perfectly fit as the network’s EMC.

— Keep feeding until full, and you get the amount of food.

Empirical Analysis

To comprehensively analyze the factors affecting the flexibility of neural networks, researchers considered various datasets, architectures, and optimizers.

Datasets

The experiments used visual datasets such as MNIST, CIFAR-10, CIFAR-100, and ImageNet, as well as tabular datasets like Forest-Cover Type, Adult Income, and Credit.

Additionally, larger synthetic datasets were used, generating high-quality image datasets with a resolution of 128×128 through efficient diffusion training using a Min-SNR weighting strategy—ImageNet-20MS, containing 20 million samples across 10 categories.

Models

The experiments evaluated multi-layer perceptrons (MLP), CNN architectures like ResNet and EfficientNet, as well as Transformer architectures like ViT.

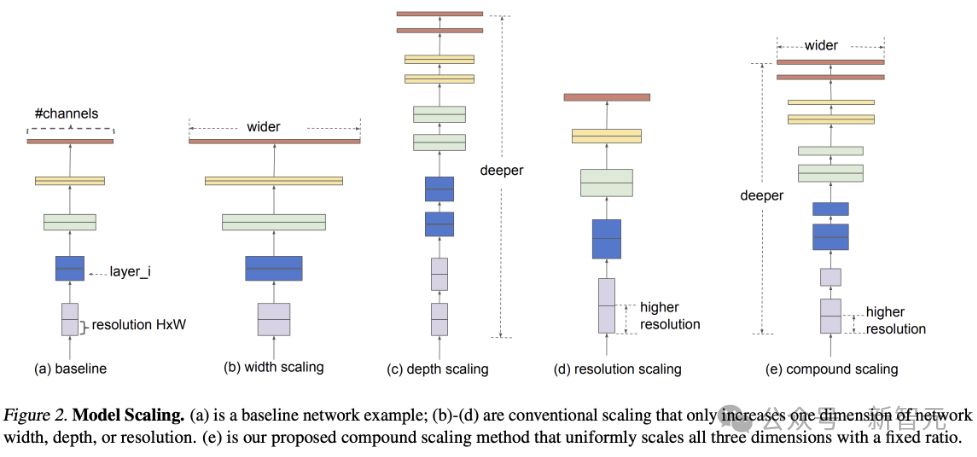
The authors systematically adjusted the width and depth of these architectures:

For MLP, width was increased by adding neurons to each layer while keeping the number of layers constant, or by adding more layers while keeping the number of neurons per layer constant.

For general CNNs (multiple convolutional layers followed by a fixed-size fully connected layer), the number of kernels per layer or the total number of convolutional layers can be changed.

For ResNet, the number of kernels or blocks (depth) can be altered.

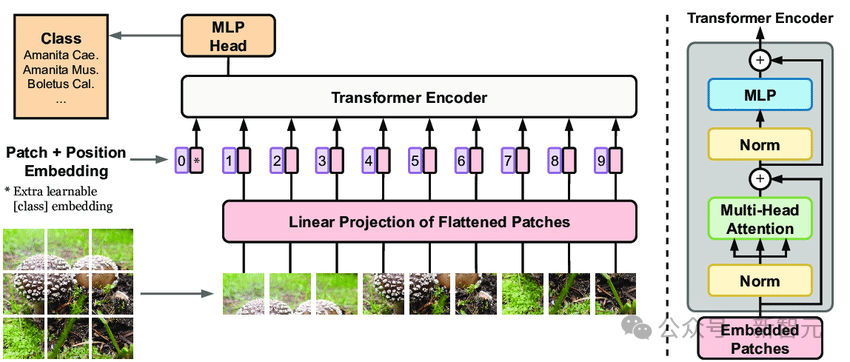
For ViT, the number of encoder layers (depth), patch embedding dimensions, and self-attention (width) can be modified.

Optimizers

The optimizers used in the experiments included Stochastic Gradient Descent (SGD), Adam, AdamW, full-batch Gradient Descent, and second-order Shampoo optimizer.

As a result, researchers could test how randomness and preprocessing features affect the minima. Additionally, to ensure effective optimization across datasets and model sizes, researchers carefully adjusted the learning rates and batch sizes for each setting and omitted weight decay.

The Impact of Data on EMC

Researchers expanded a 2-layer MLP by modifying the width of the hidden layers, expanded CNNs by altering the number of layers and channels, and trained models on a series of image (MNIST, CIFAR-10, CIFAR-100, ImageNet) and tabular (CoverType, Income, and Credit) datasets.

The results showed significant differences in EMC among networks trained on different data types:

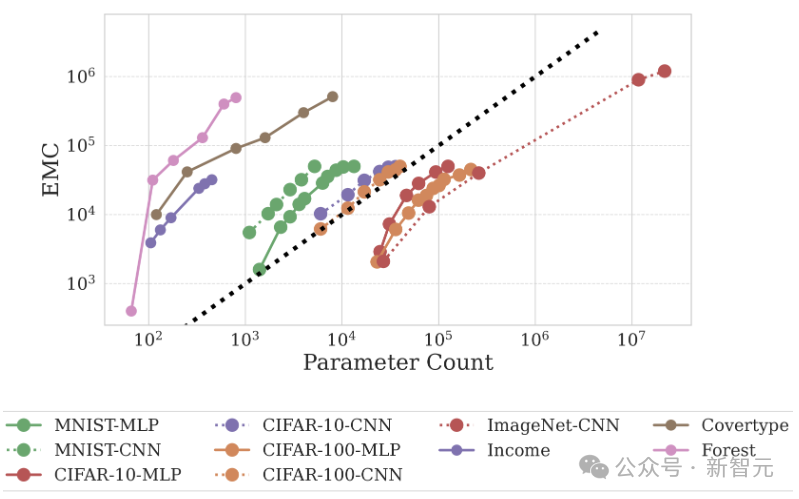
Networks trained on tabular datasets exhibited higher capacity; in image classification datasets, there was a strong correlation between test accuracy and capacity.

Notably, the EMC generated from MNIST (where the model achieved over 99% test accuracy) was the highest, while ImageNet had the lowest EMC, indicating the relationship between generalization and data fitting ability.

The Role of Inputs and Labels

Here, by changing the number of neurons or kernels in each layer, the width of MLPs and CNNs was adjusted, and training was conducted on the synthetic dataset ImageNet-20MS.

The experiments tested EMC under four conditions: semantic labels, random labels, random inputs (Gaussian noise), and inputs under fixed random arrangements.

The purpose of assigning random labels (instead of true labels) was to explore the boundary between overparameterization and underparameterization.

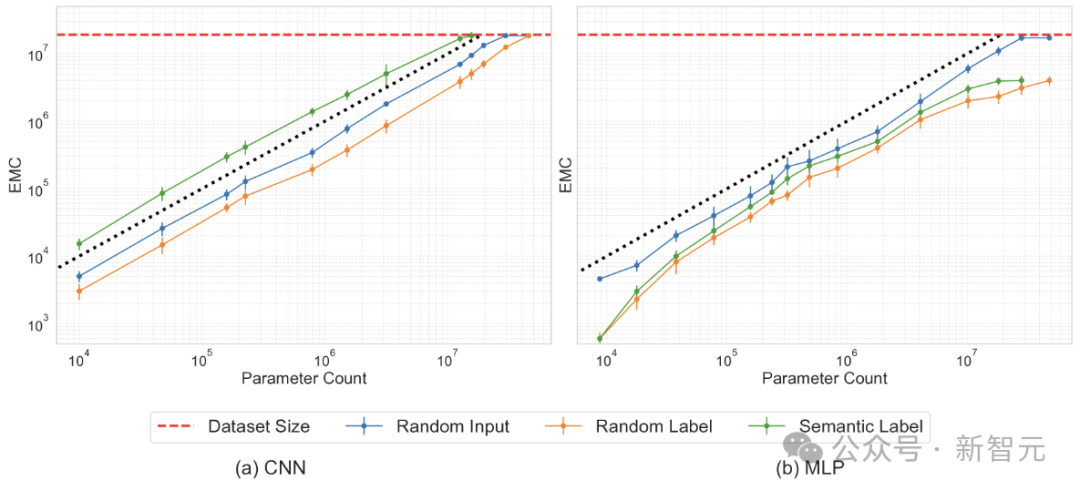
From the results above, it can be observed that when random labels are assigned compared to original labels, the network fits significantly fewer samples, and the parameter efficiency of the neural network is lower than that of linear models. Overall, the relationship between the model’s parameter count and the amount of data fitted is roughly linear.

The Impact of Class Count on EMC

The authors randomly merged categories in CIFAR-100 (keeping the original dataset size) and conducted experiments on a 2-layer CNN with different numbers of kernels.

The results are shown above; as the number of classes increases, the data with semantic labels becomes increasingly difficult to fit because the model must encode each sample in its weights.

In contrast, the data with random labels becomes easier to fit because the model is no longer forced to assign the same class labels to semantically different samples.

Prediction Generalization

Neural networks tend to fit semantically coherent labels rather than random labels, and the proficiency of the network in fitting semantic labels is usually related to its generalization ability compared to random labels.

This generalization also allows architectures like CNN to fit more samples than the number of model parameters.

Traditional machine learning concepts suggest that high-capacity models often overfit, thus affecting their generalization to new data, while PAC-Bayes theory indicates that models prefer correctly labeled data.

This article’s experiments connect these two theories.

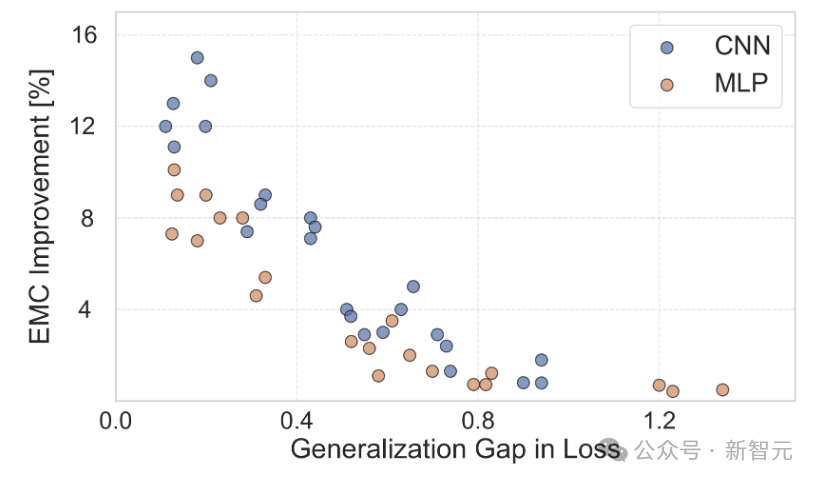
In the figure above, various CNNs and MLPs’ EMC were calculated on correctly labeled and randomly labeled data, measuring the percentage increase in EMC when the model encountered semantic labels versus random labels.

The results show a significant negative correlation between the percentage increase in EMC and the generalization gap, confirming the theoretical foundation of generalization while clarifying its practical significance.

The Impact of Model Architecture on EMC

There has always been a debate about the efficiency and generalization capabilities of CNNs and ViTs.

Experiments show that CNNs, characterized by hard-coded inductive biases, outperform ViTs and MLPs in EMC. This advantage persists across all model sizes when evaluating semantic labeled data.

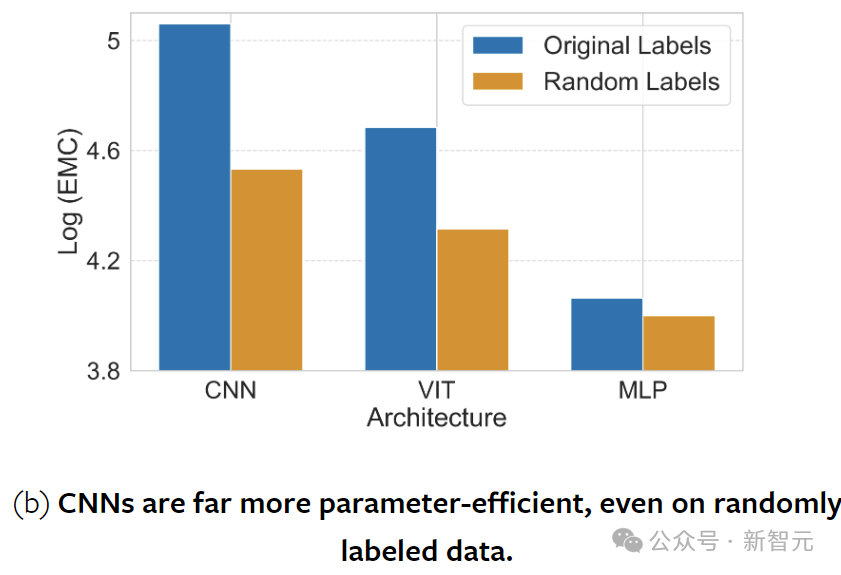
CNNs benefit greatly from data with spatial structure; when this spatial structure is disrupted by arrangement, the number of samples fitted decreases. In contrast, MLPs lack this preference for spatial structure, thus their ability to fit data remains unchanged.

Additionally, replacing inputs with Gaussian noise can increase the capacity of both architectures, which can be interpreted as, in high dimensions, noisy data is far apart, making it easier to separate.

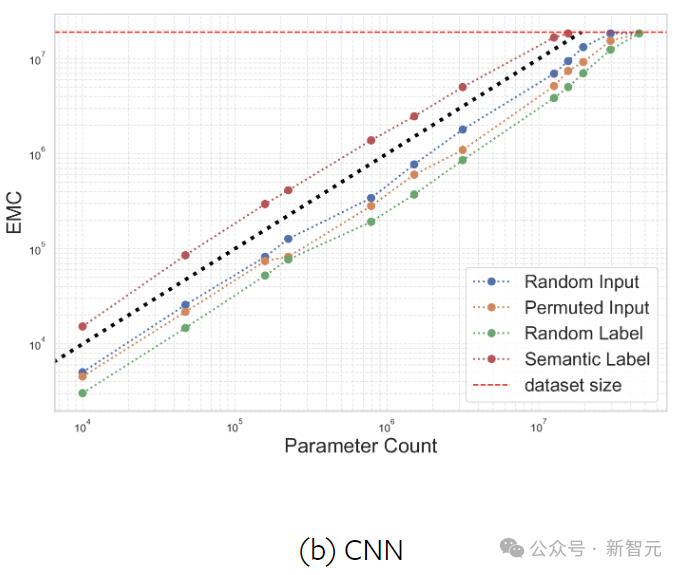
Notably, compared to random inputs, CNNs can fit many more samples with semantic labels, while MLPs are just the opposite, further highlighting CNNs’ superior generalization ability in image classification.

Expanding Network Size

The figure below shows EMC under various expansion configurations.

For ResNet, expansion measures include increasing width (number of kernels) and increasing depth. EfficientNet scales depth, width, and resolution simultaneously with a fixed coefficient. ResNet-RS adjusts scaling based on model size, training duration, and dataset size.

For ViT, SViT and SoViT methods were used, attempting to change the number of encoder blocks (depth) and patch embedding dimensions and self-attention (width) respectively.

Analysis shows that scaling depth is more parameter-efficient than scaling width. This conclusion also applies to randomly labeled data, indicating it is not merely a product of generalization.

Activation Functions

Non-linear activation functions are crucial for the capacity of neural networks; without them, neural networks are just large factored linear models.

Research findings indicate that ReLU significantly enhances model capacity. While its initial role was to alleviate gradient vanishing and explosion, ReLU also improves the network’s data fitting ability.

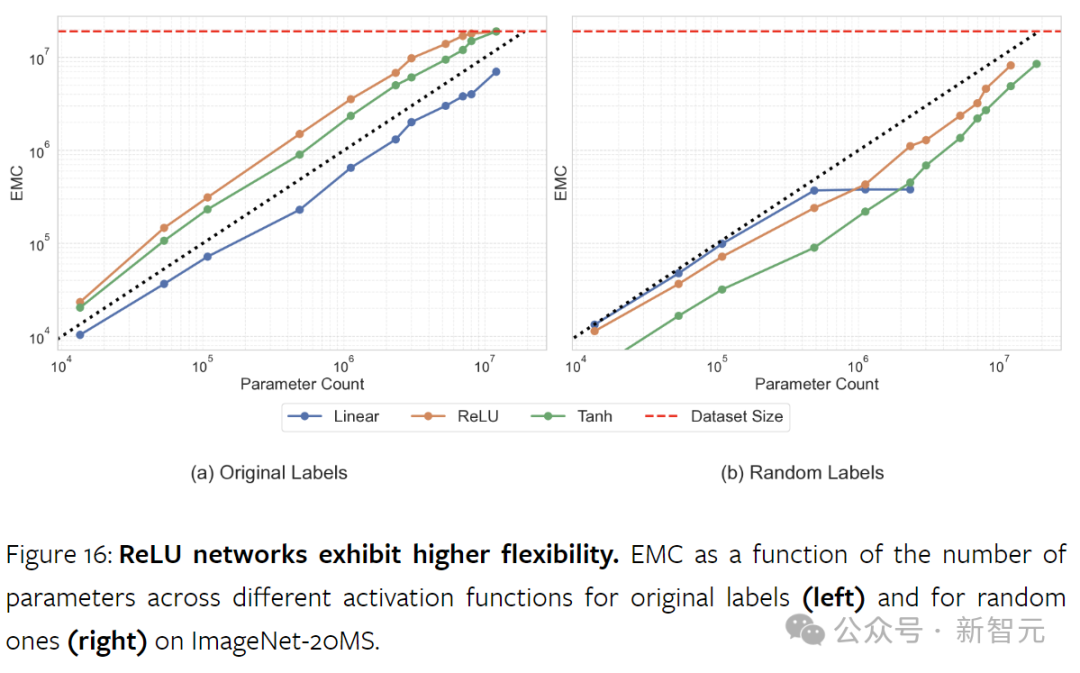
In contrast, while tanh is also non-linear, it cannot achieve similar effects.

The Role of Optimization in Fitting Data

The choice of optimization techniques and regularization strategies is crucial in neural network training. This choice not only affects training convergence but also the nature of the solutions found.

The optimizers involved in the experiments included SGD, full-batch Gradient Descent, Adam, AdamW, and Shampoo.

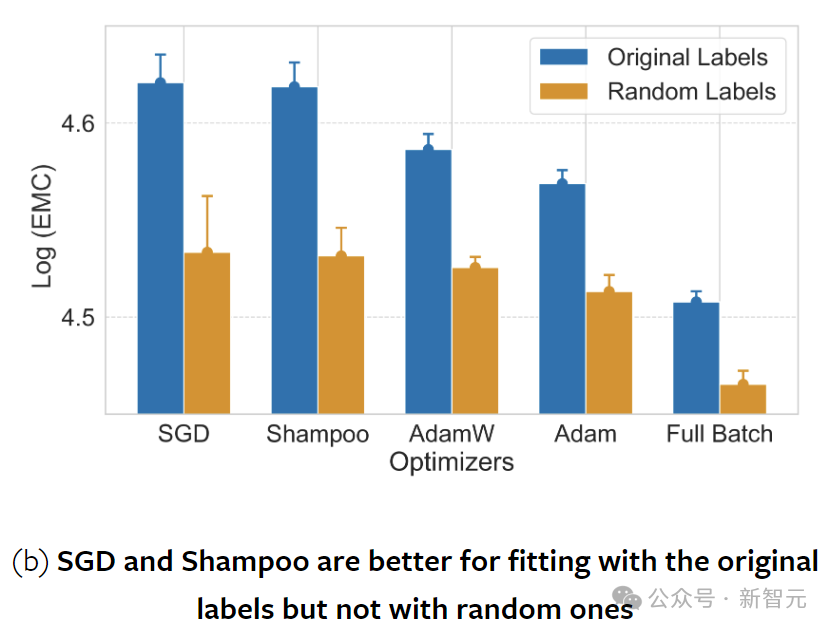
Previous research suggested that SGD has a strong flatness-seeking regularization effect, but the above figure shows that SGD can also fit more data than full-batch (non-random) gradient descent training.

Measurements of EMC for different optimizers indicate that optimizers differ not only in convergence rates but also in the types of minima found.

References:

https://x.com/micahgoldblum/status/1803088886513496392