
AliMei Guide
Learn about Transformer, and come write one with the author.
1. Preparation Knowledge
Using a model to predict second-hand house prices, let’s first understand the core concepts in machine learning.
1.1, Manual Version
1. Prepare Training Data
# Number of samples
num_examples = 1000
# Number of features: house size, age
num_input = 2
# Linear regression model, 2 W parameters values: 2, -3.4
true_w = [2, -3.4]
# 1 b parameter value
true_b = 4.2
# Randomly generate samples: feature values
features = torch.randn(num_examples, num_input, dtype=torch.float32)
# print(features[0])
# Randomly generate samples: y values
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
# print(labels[0])
# Randomly generate a batch of data, randomizing y values again
_temp = torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float32)
labels = labels + _temp
# print(labels[0])2. Define Model
# Model parameters w: w1, w2, b: b, initialized
w = torch.tensor(np.random.normal(0, 0.01, (num_input, 1)), dtype=torch.float32)
b = torch.zeros(1, dtype=torch.float32)
# Set to require gradient calculation
w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)
# Linear regression model: define torch.mm(X, w) + b, mm is matrix multiplication (m: multiply abbreviation)
def linreg(X, w, b):
return torch.mm(X, w) + b
# Define loss function: y_pred=predicted value, y=true value, simplest squared error
def squared_loss(y_pred, y):
return (y_pred - y.view(y_pred.size())) ** 2 / 2
# Define gradient descent algorithm: sgd
# params are parameters (data is parameter value, grad is gradient value), lr is learning rate, batch is size
# Why divide by batch? Because this gradient value is accumulated over batch data.
def sgd(params, lr, batch):
for param in params:
# Note that param.data is used to change param
param.data -= lr * param.grad / batch3. Train Model
# Initial learning rate
lr = 0.03
# Number of training epochs
epoch = 5
# Network: one layer, 2 inputs (2 parameters w1, w2), 1 b parameter
net = linreg
# Loss function
loss = squared_loss
# Batch size
batch_size = 10
# Training the model requires a total of epoch iterations
for epoch in range(epoch):
# In each iteration, all samples run from 0~1000, each batch=10
for X, y in data_iter(batch_size, features, labels):
# ls is the sum of losses for this batch
ls = loss(net(X, w, b), y).sum()
# Calculate gradient value
ls.backward()
# Update parameters
sgd([w, b], lr, batch_size)
# Don’t forget to zero gradients for the next time
w.grad.data.zero_()
b.grad.data.zero_()
# After completing this round of training, print loss to observe it decreasing
train_l = loss(net(features, w, b), labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))Auxiliary function: by batch & random, read sample data
# Define random reading of data by batch
def data_iter(batch, features, labels):
nums = len(features) # Get the number of samples
# Generate 0-1000 array
indices = list(range(nums)) # Generate index list
# Shuffle the reading order of indices
random.shuffle(indices) # Shuffle the indices
# Generate: start=0, stop=1000, step=batch=10
for i in range(0, nums, batch):
# Slice a segment of indices, size=batch
t_ind = indices[i: min(i + batch, num_examples)] # Last one may not be a full batch
# Convert to tensor format required by torch: tensor
j = torch.LongTensor(t_ind)
# Find from vector according to indices
# yield: generates an iterator return, similar to a closure, returns once per call, and continues from the last paused position on the next call
yield features.index_select(0, j), labels.index_select(0, j)1.2, Pytorch Version
1. Prepare Training Data
2. Define Model
# Define model: linear regression
class LinearNet(nn.Module):
def __init__(self, n_feature):
super(LinearNet, self).__init__()
# Linear planning: n_feature=number of w, 1=1 b
self.linear = nn.Linear(n_feature, 1)
# forward defines [forward propagation]
def forward(self, x):
y = self.linear(x)
return y
# Instantiate model, initialize parameters
net = LinearNet(num_input)
init.normal_(net[0].weight, mean=0, std=0.01)
init.constant_(net[0].bias, val=0)
# Define loss function
loss = nn.MSELoss()
# Define gradient descent algorithm (lr is learning rate)
optimizer = optim.SGD(net.parameters(), lr=0.03)3. Train Model
num_epochs = 3
for epoch in range(1, num_epochs + 1):
for X, y in data_iter:
output = net(X)
# Calculate loss value
l_sum = loss(output, y.view(-1, 1))
# Update gradients
l_sum.backward()
# Update w and b
optimizer.step()
# Zero gradients
optimizer.zero_grad()
print('epoch %d, loss: %f' % (epoch, l_sum.item()))Batch reading data
# Read data by batch & random
batch_size = 10
data_set = Data.TensorDataset(features, labels)
data_iter = Data.DataLoader(data_set, batch_size, shuffle=True)a. nn.Module and forward() function: represents a layer in the neural network, overrides init and forward methods (Question: how to implement a 2-layer network?)
2. Handwriting Transformer
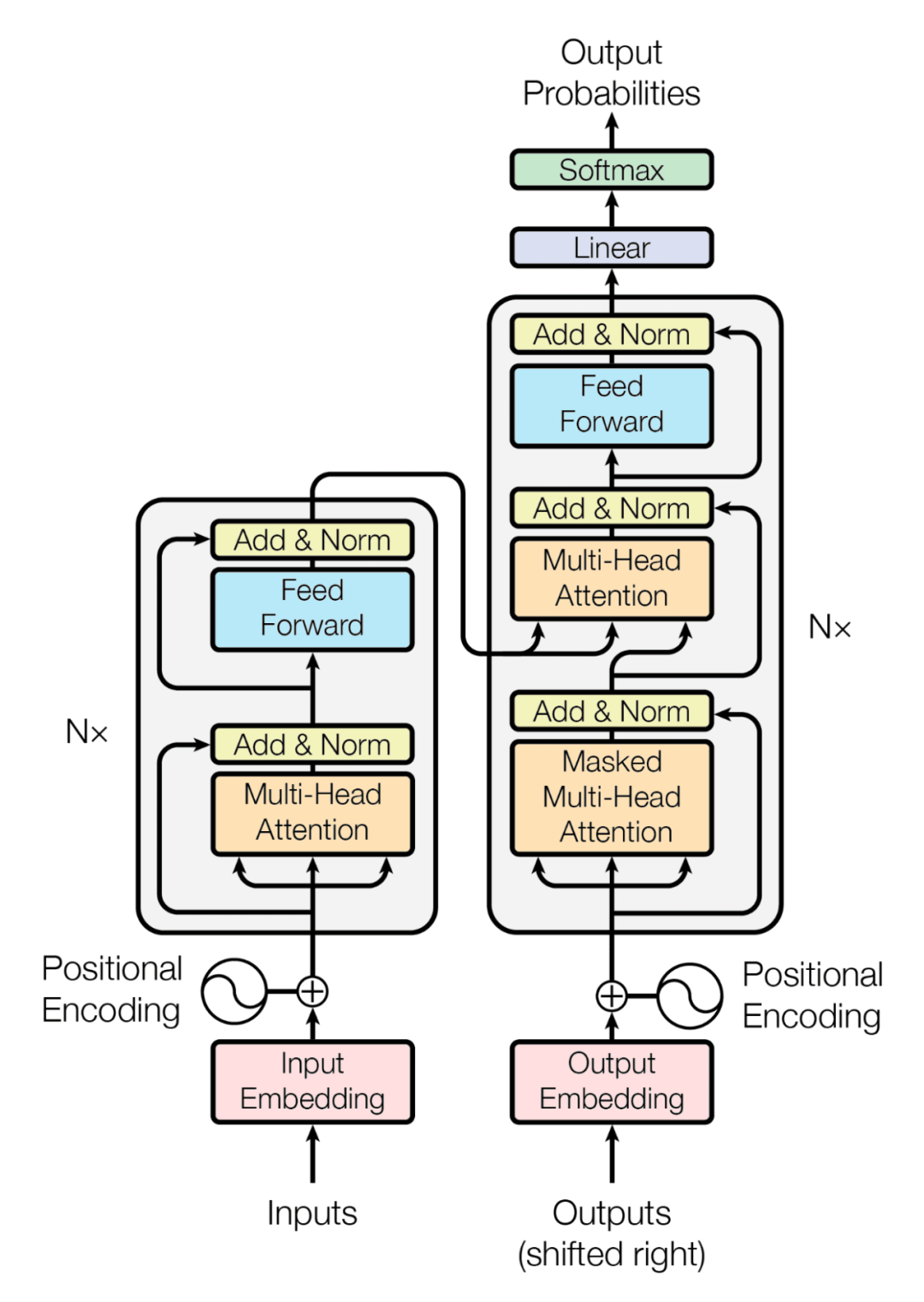
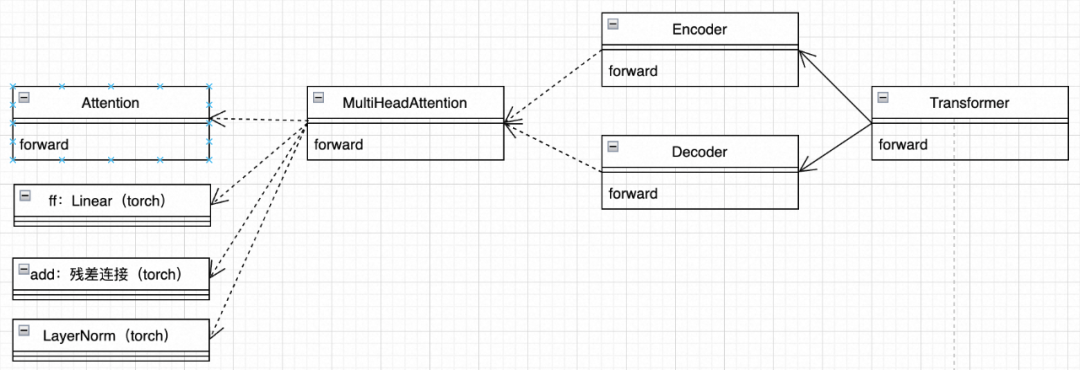
2.1, Example: Translation
# Define dictionary
source_vocab = {'E': 0, '我': 1, '吃': 2, '肉': 3}
target_vocab = {'E': 0, 'I': 1, 'eat': 2, 'meat': 3, 'S': 4}
# Sample data
encoder_input = torch.LongTensor([[1, 2, 3, 0]]).to(device) # 我 吃 肉 E, E represents the end word
decoder_input = torch.LongTensor([[4, 1, 2, 3]]).to(device) # S I eat meat, S represents the start word, and is shifted right for parallel training
target = torch.LongTensor([[1, 2, 3, 0]]).to(device) # I eat meat E, translation targetAccording to the class diagram above, let’s implement it step by step
1. Attention
class ScaledDotProductAttention(nn.Module):
def __init__(self):
super(ScaledDotProductAttention, self).__init__()
def forward(self, Q, K, V, attn_mask):
# Q, K, V have already been multiplied by W(q), W(k), W(v) matrices
# As shown in the diagram, but no need to calculate one by one, matrix multiplication handles it all at once
scores = torch.matmul(Q, K.transpose(-1, -2)) / np.sqrt(d_k)
# Set the values in the masked area to near 0, indicating E end or decoder self-order masking, attention is discarded
scores.masked_fill_(attn_mask, -1e9)
# After softmax (masked area becomes 0)
attn = nn.Softmax(dim=-1)(scores)
# The product means: bringing attention information to V. prob is the z in the diagram (matrix calculation does not need to be v1+v2).
prob = torch.matmul(attn, V)
return prob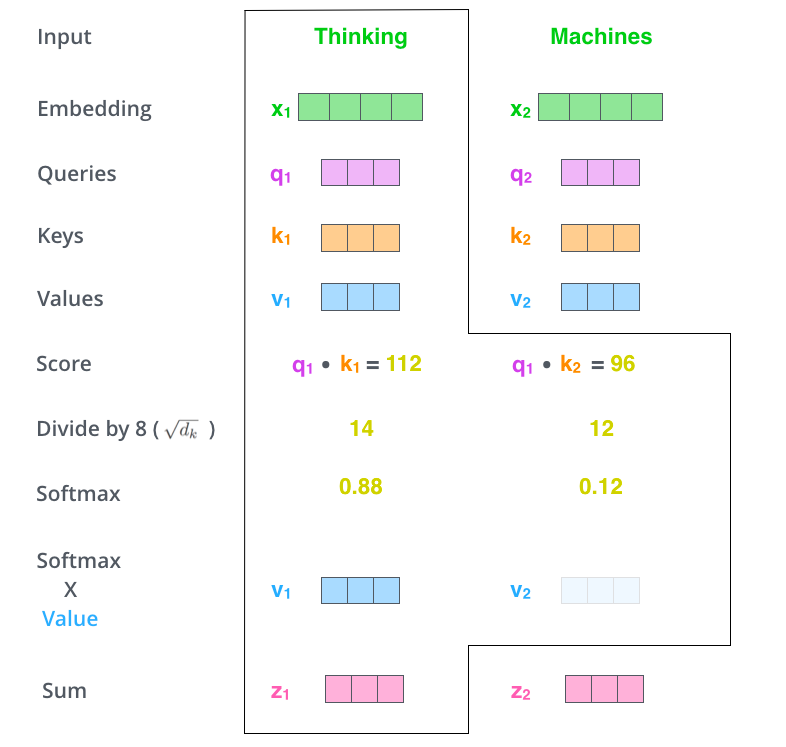
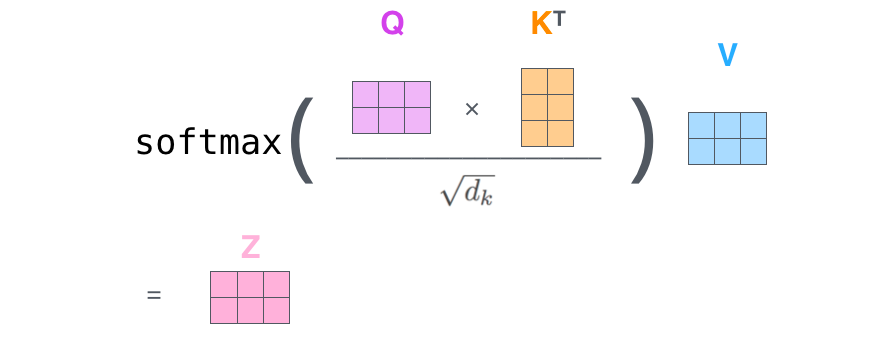
2. MultiHeadAttention
General variable definitions
d_model = 6 # embedding size
d_ff = 12 # feedforward neural network dimension
d_k = d_v = 3 # dimension of k (same as q) and v
n_heads = 2 # number of heads in multihead attention
# n_heads = 1 # number of heads in multihead attention [Note: To simplify debugging, it can be changed to 1 head]
p_drop = 0.1 # probability of dropout
device = "cpu"Note 1: By inertia, one might think there will be multiple heads and serial loop calculations, but no, multiple heads are a tensor input
Note 2: FF fully connected, residual connection, normalization, lines 35, 38 industry code, simplification brought by the pytorch framework
class MultiHeadAttention(nn.Module):
def __init__(self):
super(MultiHeadAttention, self).__init__()
self.n_heads = n_heads
self.W_Q = nn.Linear(d_model, d_k * n_heads, bias=False)
self.W_K = nn.Linear(d_model, d_k * n_heads, bias=False)
self.W_V = nn.Linear(d_model, d_v * n_heads, bias=False)
self.fc = nn.Linear(d_v * n_heads, d_model, bias=False) # FF fully connected
self.layer_norm = nn.LayerNorm(d_model) # normalization
def forward(self, input_Q, input_K, input_V, attn_mask):
# input_Q: 1*4*6, each batch 1 sentence * each sentence 4 words * each word 6 length encoding
# residual temporarily saves the original value for later residual connection addition
residual, batch = input_Q, input_Q.size(0)
# Multiply by W matrix. Note: The dimension changes from 2D to 3D, increasing the head dimension, also parallel computation at once
Q = self.W_Q(input_Q) # Multiply by W(6*6) becomes 1*4*6
Q = Q.view(batch, -1, n_heads, d_k).transpose(1, 2) # Split into 2 Heads becomes 1*2*4*3 1 batch 2 Heads 4 words 3 encodings
K = self.W_K(input_K).view(batch, -1, n_heads, d_k).transpose(1, 2)
V = self.W_V(input_V).view(batch, -1, n_heads, d_v).transpose(1, 2)
# 1*2*4*4, 2 Heads of 4*4, the last column is true
# Because the last column is the E end symbol
attn_mask = attn_mask.unsqueeze(1).repeat(1, n_heads, 1, 1)
# Returns 1*2*4*3, 2 heads, 4*3 with attention relationships for 4 words
prob = ScaledDotProductAttention()(Q, K, V, attn_mask)
# Concatenate the 2 heads back together to become 1*4*6
prob = prob.transpose(1, 2).contiguous()
prob = prob.view(batch, -1, n_heads * d_v).contiguous()
# Fully connected layer: performs a linear transformation on the output of multi-head attention to better extract information
output = self.fc(prob)
# Residual connection & normalization
res = self.layer_norm(residual + output) # return 1*4*6
return res3. Encoder
In the attention concept, there is a key concept of “masking” that we won’t delve into now; debugging it will help you understand better.
def get_attn_pad_mask(seq_q, seq_k): # Essentially masking the end E for attention, returns 1*4*4, the last column is true
batch, len_q = seq_q.size() # 1, 4
batch, len_k = seq_k.size() # 1, 4
pad_attn_mask = seq_k.data.eq(0).unsqueeze(1) # If 0, then true, becomes f,f,f,true, meaning ignore the ending corresponding attention
return pad_attn_mask.expand(batch, len_q, len_k) # Expand to 1*4*4, the last column true indicates the end corresponding attention is discarded
def get_attn_subsequent_mask(seq): # decoder self-order attention masking, upper triangular area is true
attn_shape = [seq.size(0), seq.size(1), seq.size(1)]
subsequent_mask = np.triu(np.ones(attn_shape), k=1)
subsequent_mask = torch.from_numpy(subsequent_mask)
return subsequent_maskclass Encoder(nn.Module):
def __init__(self):
super(Encoder, self).__init__()
self.source_embedding = nn.Embedding(len(source_vocab), d_model)
self.attention = MultiHeadAttention()
def forward(self, encoder_input):
# input 1 * 4, 1 sentence with 4 words
# 1 * 4 * 6, expands each word's integer encoding to 6 floating-point encodings
embedded = self.source_embedding(encoder_input)
# 1 * 4 * 4 matrix, the last column is true, indicating ignore the ending word's attention mechanism
mask = get_attn_pad_mask(encoder_input, encoder_input)
# 1*4*6, the 4 words matrix with attention
encoder_output = self.attention(embedded, embedded, embedded, mask)
return encoder_outputclass Decoder(nn.Module):
def __init__(self):
super(Decoder, self).__init__()
self.target_embedding = nn.Embedding(len(target_vocab), d_model)
self.attention = MultiHeadAttention()
# The three input shapes are 1*4, 1*4, 1*4*6, the last one is the encoder_output
def forward(self, decoder_input, encoder_input, encoder_output):
# Encoded to 1*4*6
decoder_embedded = self.target_embedding(decoder_input)
# 1*4*4 all false, indicating no end word
decoder_self_attn_mask = get_attn_pad_mask(decoder_input, decoder_input)
# 1*4*4 upper triangular area is 1, others are 0
decoder_subsequent_mask = get_attn_subsequent_mask(decoder_input)
# 1*4*4 upper triangular area true, others false
decoder_self_mask = torch.gt(decoder_self_attn_mask + decoder_subsequent_mask, 0)
# 1*4*6 words matrix with attention [Note: In decoder, this is the first attention]
decoder_output = self.attention(decoder_embedded, decoder_embedded, decoder_embedded, decoder_self_mask)
# 1*4*4 last column true, indicating E end word
decoder_encoder_attn_mask = get_attn_pad_mask(decoder_input, encoder_input)
# All inputs are 1*4*6, Q represents "S I eat meat", K represents "我吃肉E", V represents "我吃肉E"
# [Note: In decoder, this is the second attention]
decoder_output = self.attention(decoder_output, encoder_output, encoder_output, decoder_encoder_attn_mask)
return decoder_output5. Transformer
class Transformer(nn.Module):
def __init__(self):
super(Transformer, self).__init__()
self.encoder = Encoder()
self.decoder = Decoder()
self.fc = nn.Linear(d_model, len(target_vocab), bias=False)
def forward(self, encoder_input, decoder_input):
# Input 1*4, output 1*4*6, function: "我吃肉E", and brings attention information among the three words
encoder_output = self.encoder(encoder_input)
# Input 1*4, 1*4, 1*4*6=encoder_output
decoder_output = self.decoder(decoder_input, encoder_input, encoder_output)
# Predict 4 words, each word corresponds to the probability in the vocabulary
decoder_logits = self.fc(decoder_output)
res = decoder_logits.view(-1, decoder_logits.size(-1))
return resmodel = Transformer().to(device)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=1e-1)
for epoch in range(10):
# Output 4*5, representing the predicted 4 words, each corresponding to the probability of 5 words in the vocabulary
output = model(encoder_input, decoder_input) # Calculate the difference with the target word I eat meat E
loss = criterion(output, target.view(-1))
print('Epoch:', '%04d' % (epoch + 1), 'loss =', '{:.6f}'.format(loss))
# These three operations: zero gradients, calculate gradients, update parameters
optimizer.zero_grad()
loss.backward()
optimizer.step()# Predict target is 5 words
target_len = len(target_vocab) # 1*4*6 Input "我吃肉E", first calculate [self-attention]
encoder_output = model.encoder(encoder_input) # 1*5 all 0, indicating EEEEE
decoder_input = torch.zeros(1, target_len).type_as(encoder_input.data) # Indicates S start character
next_symbol = 4 # 5 words are predicted one by one [Note: This means predicting one by one]
for i in range(target_len):
# For example, in the first round when i=0, the decoder input is SEEEE, in the second round it is S I EEE, adding the predicted I, continue looping
decoder_input[0][i] = next_symbol
# Decoder output
decoder_output = model.decoder(decoder_input, encoder_input, encoder_output)
# Responsible for mapping the decoder output to the target vocabulary, each element represents the score corresponding to the target word
# Take the largest five words’ indices, e.g. [1, 3, 3, 3, 3] indicates i,meat,meat,meat,meat
logits = model.fc(decoder_output).squeeze(0)
prob = logits.max(dim=1, keepdim=False)[1]
next_symbol = prob.data[i].item() # Only take current i
for k, v in target_vocab.items():
if v == next_symbol:
print('Round', i, ':', k)
break
if next_symbol == 0: # When the end is reached, the translation is complete
breakReferences:
3, gpt4: During the learning process, there were many doubts, it is indeed a good teacher
Aliyun Developer Community, the choice of millions of developers
Aliyun Developer Community, millions of quality technical content, thousands of free system courses, rich experience scenarios, active community activities, industry experts sharing and communication, welcome to click [Read Original] to join us.
