1. Grok-3 Claims to Prove the Riemann Hypothesis and the Attention It Has Drawn
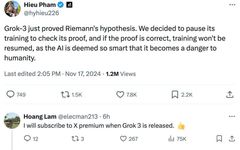
In 2024, Hieu Pham, an engineer from Elon Musk’s AI startup xAI, shocked the social media world by announcing that the company’s third-generation AI model, Grok-3, has successfully proven the long-standing mathematical Riemann Hypothesis. This news hit the mathematics and technology communities like a bombshell. Originally scheduled for release in December 2024, this leak has instantly focused attention on this powerful AI model.
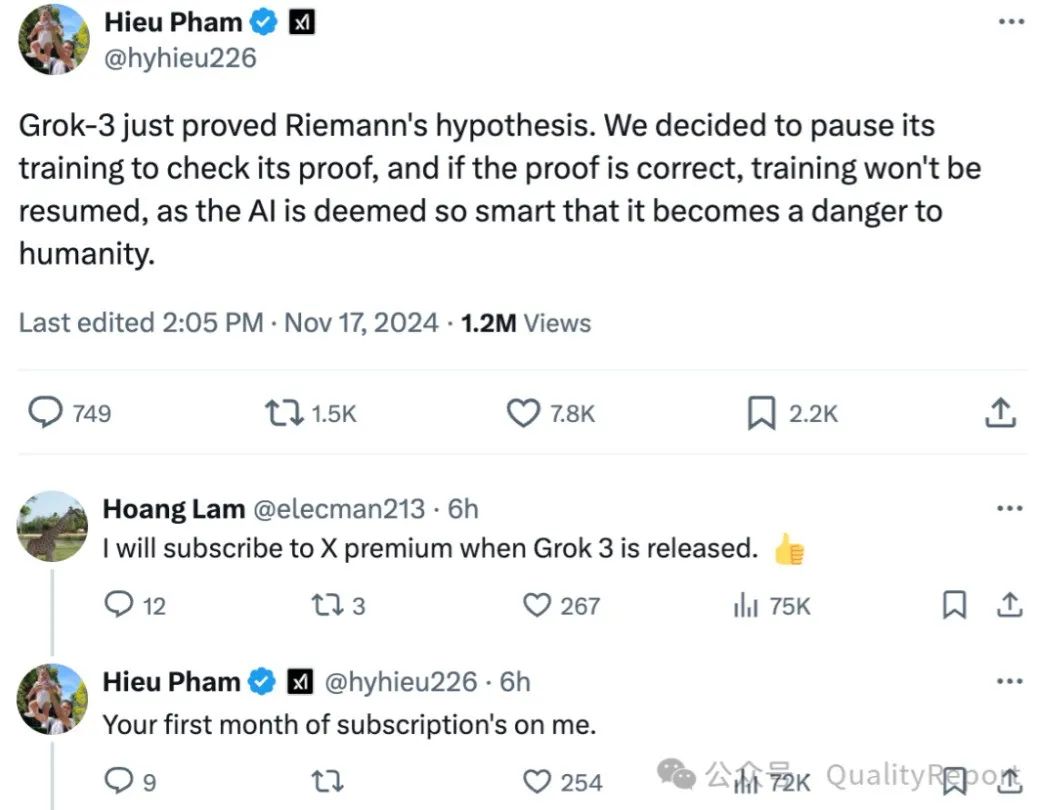
xAI made a bold decision: they will suspend further training of Grok-3 until this proof is verified, as they are concerned that the model may have developed beyond human control. It is worth noting that Grok-3’s training utilized 100,000 of Nvidia’s latest H100 GPUs, showcasing xAI’s ambition and significant investment in the AI field. The financial investment alone in GPUs may reach nearly $3 billion, raising expectations about Grok-3’s capabilities.
This event not only amazed people regarding Grok-3’s intelligence level but also sparked deep reflections on the potential and risks of AI development. If Grok-3 has indeed proven the Riemann Hypothesis, it would represent a major breakthrough in the field of artificial intelligence, profoundly impacting mathematics, cryptography, physics, and other disciplines.
2. Introduction to the Riemann Hypothesis
The Riemann Hypothesis was first proposed by the German mathematician Bernhard Riemann in 1859 and is a core problem in number theory. In a paper titled “On the Number of Primes Less Than a Given Value,” Riemann discussed the distribution of prime numbers using functions and proposed the Riemann Hypothesis. This hypothesis primarily concerns the distribution of the non-trivial zeros of the Riemann zeta function, stating that all non-trivial zeros of the Riemann zeta function lie on the critical line where the real part equals 1/2.
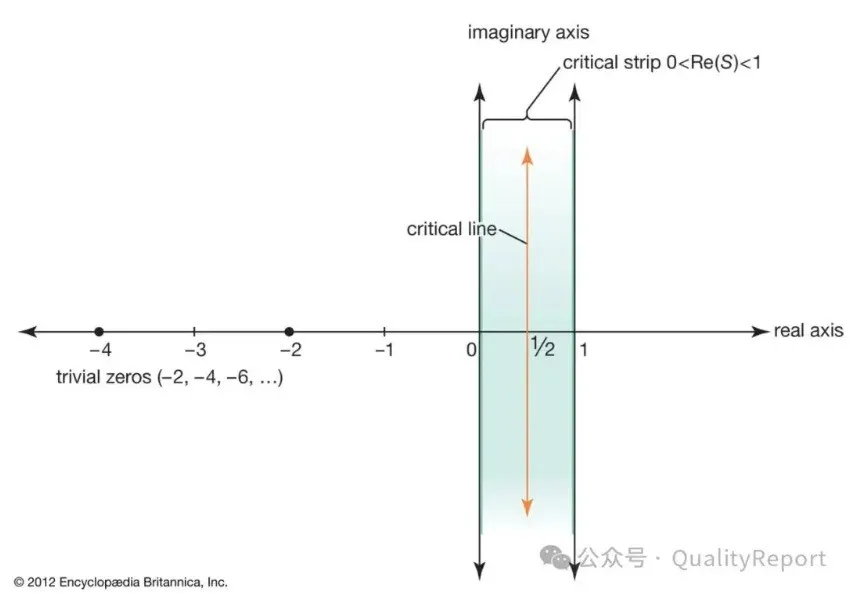
The Riemann zeta function is a complex function that was initially a generalization of series. When the variable in the series is extended from real numbers to complex numbers, the function becomes more complex and interesting. For certain complex numbers, the zeta function evaluates to zero, and determining the specific locations of these zeros in the complex plane is one of the most challenging problems in mathematics. Among them, it is easy to prove that the zeta function evaluates to zero for all negative even integers; these zeros are called trivial zeros. The Riemann Hypothesis focuses on the distribution of non-trivial zeros.
The importance of the Riemann Hypothesis is self-evident. It is one of the most significant unsolved problems in mathematics, profoundly influencing the development of function theory and number theory. Much work in number theory and the field of complex functions is based on the assumption that the Riemann Hypothesis is true; thus, once the Riemann Hypothesis is proven, many other related works will also be completely proven. For example, solving the Riemann Hypothesis may help resolve other famous mathematical problems such as the Goldbach Conjecture. Because of this, the Riemann Hypothesis is listed as one of the seven Millennium Prize Problems by the Clay Mathematics Institute, attracting the attention of countless outstanding mathematicians.
3. Historical Claims of Solving the Riemann Hypothesis
1903 Gelfond’s Research: In 1903, Gelfond proved that the first 15 zeros of the Riemann zeta function supported the validity of the Riemann Hypothesis, marking one of the earliest achievements in this area of research. Although this was only a preliminary verification, it provided important reference and confidence for subsequent studies. Since then, mathematicians have continuously worked to verify whether more zeros conform to the Riemann Hypothesis.
1989 Conley’s Research: In 1989, American mathematician Conley proved that at least 40% of the zeros lie on the critical line. This was a significant advancement in the study of the Riemann Hypothesis, further supporting its correctness. However, this was still only a partial result and could not fully prove that all non-trivial zeros lie on the critical line.
2018 Michael Atiyah’s Claim: On September 20, 2018, mathematician Michael Atiyah claimed to have proven the Riemann Hypothesis. At the Heidelberg Forum, Sir Atiyah explained the essence of the Riemann Hypothesis and its relation to prime numbers, presenting a simple idea for proving the Riemann Hypothesis, inspired by his derivation of the fine structure constant at the 2018 ICM. However, since this paper has not yet undergone peer review, some scholars are skeptical of his derivation or proof process. Nevertheless, Atiyah’s attempt has provided a new perspective for cracking the Riemann Hypothesis.
2024 Breakthrough by Guth and Maynard: In May 2024, MIT mathematics professor Larry Guth and Fields Medalist James Maynard achieved a significant breakthrough regarding the Riemann Hypothesis. They established a new upper limit on the number of specific types of exceptions, breaking a record that had stood for over 80 years, resulting in a better approximation of the number of primes in short intervals on the number line and potentially providing more insights into prime behavior. Although this is still far from completely solving the Riemann Hypothesis, it remains a historic moment.
4. Deep Reflections on the Grok-3 Incident
4.1 The Potential of AI in Mathematical Proofs
Artificial intelligence has already demonstrated remarkable capabilities in the field of mathematics:
1. In 2020, DeepMind’s AI system made breakthroughs in combinatorial mathematics problems.
2. In 2022, machine learning algorithms helped discover new mathematical theorems.
3. In 2023, multiple AI systems made progress in assisting mathematical proofs.
4.2 Reasons to Exercise Caution
However, the academic community generally maintains a cautious attitude toward the news that Grok-3 may have proven the Riemann Hypothesis:
1. The rigor required for mathematical proofs is extremely high and needs to undergo strict peer review.
2. AI-generated “proofs” may contain logical leaps or implicit assumptions.
3. Historical errors remind us to remain vigilant.
4. The “black box” nature of AI models may complicate verification efforts.
5. Future Outlook
Regardless of whether Grok-3’s proof is ultimately validated, this incident brings us important insights:
1. The role of AI in mathematical research is shifting from auxiliary tools to core contributors.
2. Human-machine collaboration may be a new paradigm for solving complex mathematical problems.
3. There is a need to establish new methodologies to verify AI-generated mathematical proofs.
4. Traditional mathematical research may need to adapt to the new characteristics of the AI era.
The encounter between Grok-3 and the Riemann Hypothesis is not only an important moment in the history of mathematics but also a key juncture in the development of artificial intelligence. Regardless of the final outcome, this incident will drive us to rethink AI’s role in mathematical research and the relationship between human intelligence and machine intelligence.
While waiting for expert validation, we must maintain a moderate level of skepticism while being open to the potential of AI in the field of mathematics. After all, as with many significant breakthroughs in history, revolutionary discoveries often come from unexpected places.
More Exciting:
Yan Shi | The Impact of Generative AI on Computer Science Education and Countermeasures
Principal Interview | Focusing on Teacher Training in Ethnic Minority Areas — An Interview with Principal Chen Benhui of Lijiang Normal University
Yan Shi | A Review and Prospect of Cultivating Computer System Abilities
The Concept of “Student-Centered” Teaching and Its Implementation Path
Principal Interview | Promoting Interdisciplinary Integration to Cultivate Innovative Talents in the New Era — An Interview with Professor Ni Mingxuan, Founding President of Hong Kong University of Science and Technology (Guangzhou)
The New Year Message from the Seventh Editorial Committee
Guidelines for Ideological and Political Education in Computer Science Courses
Academician Chen Guoliang | Cultural Construction of Virtual Teaching and Research Office for Computer Courses
Professor Chen Daoxu of Nanjing University | Change and Constancy: Dialectics in the Learning Process
Yan Shi | Thoughts and Suggestions on the “Predicament” of Young Teachers in Colleges and Universities
Xu Xiaofei et al. | The Metaverse Education and Its Service Ecosystem
[Table of Contents] “Computer Education” Issue 10, 2024
[Table of Contents] “Computer Education” Issue 9, 2024
[Table of Contents] “Computer Education” Issue 8, 2024
[Editorial Committee Message] Professor Li Xiaoming of Peking University: Reflections on the “Year of Classroom Teaching Improvement”…
Professor Chen Daoxu of Nanjing University: Which is more important, teaching students to ask questions or teaching students to answer questions?
[Yan Shi Series]: Trends in Computer Discipline Development and Their Impact on Computer Education
Professor Li Xiaoming of Peking University: From Fun Mathematics to Fun Algorithms to Fun Programming — A Path for Non-professional Learners to Experience Computational Thinking?
Reflections on Several Issues in Building First-Class Computer Disciplines
New Engineering and Big Data Professional Development
Learning from Others — A Compilation of Research Articles on Computer Education from China and Abroad