When adjusting the way the model updates weights and bias parameters, have you considered which optimization algorithm can yield better and faster results for the model? Should you use gradient descent, stochastic gradient descent, or the Adam method?

This article introduces the main differences between different optimization algorithms and how to choose the best optimization method.

What Are Optimization Algorithms?

The function of optimization algorithms is to minimize (or maximize) the loss function E(x) by improving the training method.

Some parameters within the model are used to calculate the deviation between the true values Y and the predicted values in the test set, based on these parameters, the loss function E(x) is formed.

For example, weights (W) and biases (b) are such internal parameters, generally used to calculate output values, playing a major role when training neural network models.

When effectively training models and producing accurate results, the internal parameters of the model play a very important role. This is why we should use various optimization strategies and algorithms to update and compute the network parameters that affect model training and output, bringing them closer to or achieving optimal values.

Optimization algorithms are divided into two main categories:

1. First-order Optimization Algorithms

This type of algorithm uses the gradient values of parameters to minimize or maximize the loss function E(x). The most commonly used first-order optimization algorithm is gradient descent.

Function gradient: the multivariable expression of the derivative dy/dx, used to represent the instantaneous rate of change of y with respect to x. Often, to calculate the derivative of multivariable functions, gradients replace derivatives and partial derivatives are used to calculate gradients. A key difference between gradients and derivatives is that the gradient of a function forms a vector field.

Thus, for single-variable functions, derivatives are used for analysis; while gradients arise from multivariable functions. More theoretical details will not be elaborated here.

2. Second-order Optimization Algorithms

Second-order optimization algorithms use the second derivatives (also known as Hessian methods) to minimize or maximize the loss function. Due to the high computational cost of second derivatives, this method is not widely used.

Detailed Explanation of Various Neural Network Optimization Algorithms

Gradient Descent

When training and optimizing intelligent systems, gradient descent is one of the most important techniques and foundations. The function of gradient descent is:

To control variance and update model parameters by finding the minimum value, ultimately leading the model to converge.

The formula for updating network parameters is: θ=θ−η×∇(θ).J(θ), where η is the learning rate, and ∇(θ).J(θ) is the gradient of the loss function J(θ).

This is the most commonly used optimization algorithm in neural networks.

Today, gradient descent is mainly used for weight updates in neural network models, i.e., updating and adjusting model parameters in one direction to minimize the loss function.

The backpropagation technique introduced in 2006 made it possible to train deep neural networks. Backpropagation calculates the product of input signals and their corresponding weights during forward propagation, then applies the activation function to the sum of these products. This method of transforming input signals into output signals is a crucial means of modeling complex nonlinear functions, introducing nonlinear activation functions that enable the model to learn almost any form of function mapping. Then, during the network’s backpropagation process, relevant errors are fed back, using gradient descent to update weight values by calculating the gradient of the error function E with respect to the weight parameters W, updating the weight parameters in the opposite direction of the loss function gradient.

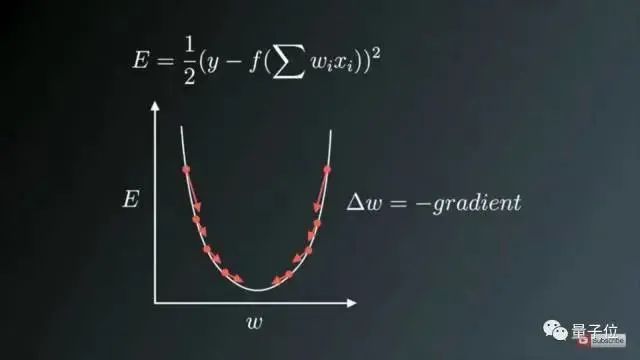
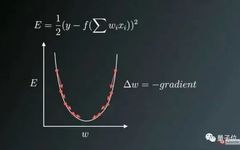
Figure 1: Direction of Weight Update Opposite to Gradient Direction

Figure 1 shows the process of weight updates in the opposite direction of the gradient vector error, where the U-shaped curve represents the gradient. It should be noted that when the weight value W is too small or too large, there will be significant errors, necessitating updates and optimization of weights to convert them into suitable values, so we try to find a local optimal value in the direction opposite to the gradient.

Variants of Gradient Descent

Traditional batch gradient descent computes the gradient of the entire dataset but only performs one update, making it slow and difficult to control when dealing with large datasets, even leading to memory overflow.

The speed of weight updates is determined by the learning rate η, and it can converge to the global optimal value in convex error surfaces, while it may tend towards local optimal values in non-convex surfaces.

Using the standard form of batch gradient descent has another issue, which is the redundant weight updates during training on large datasets.

The aforementioned issues of standard gradient descent are resolved in the stochastic gradient descent method.

1. Stochastic Gradient Descent (SGD)

Stochastic gradient descent (SGD) updates parameters for each training sample, performing an update for each execution, and thus is faster.

θ=θ−η⋅∇(θ) × J(θ;x(i);y(i)), where x(i) and y(i) are the training samples.

Frequent updates result in high variance among parameters, causing the loss function to fluctuate with varying intensities. This is actually beneficial, as it helps us discover new and potentially better local minima, while standard gradient descent will only converge to a certain local optimal value.

However, the problem with SGD is that due to frequent updates and fluctuations, it will eventually converge to a minimum limit and may experience overshooting due to the frequent fluctuations.

It has been shown that when the learning rate η is slowly reduced, the convergence pattern of standard gradient descent is similar to that of SGD.

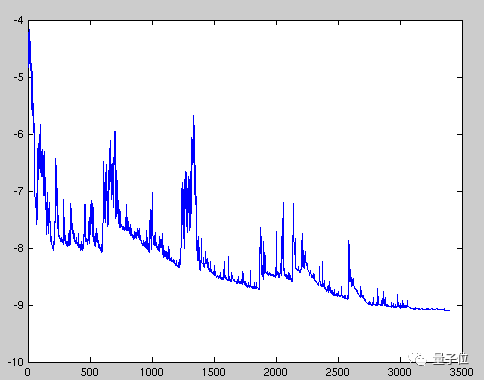
Figure 2: High Variance Parameter Updates in Each Training Sample Cause Significant Fluctuations in Loss Function, Thus We May Not Obtain the Minimum Value of the Loss Function.

Another variant known as “mini-batch gradient descent” can address the issues of high variance parameter updates and unstable convergence.

2. Mini-Batch Gradient Descent

To avoid the problems present in SGD and standard gradient descent, an improved method is mini-batch gradient descent, which performs one update for every n training samples in each batch.

The advantages of using mini-batch gradient descent are:

1) It can reduce the fluctuations of parameter updates, ultimately achieving better and more stable convergence.

2) It can also utilize common matrix optimization methods in the latest deep learning libraries, making the computation of gradients for mini-batch data more efficient.

3) Generally, the size range of mini-batch samples is from 50 to 256, which can vary depending on the actual problem.

4) When training neural networks, the mini-batch gradient descent algorithm is usually chosen.

This method is sometimes still referred to as SGD.

Challenges Faced When Using Gradient Descent and Its Variants

1. It is difficult to choose a suitable learning rate. A learning rate that is too small can lead to the network converging too slowly, while a learning rate that is too large may affect convergence and cause the loss function to fluctuate around the minimum value, or even lead to gradient divergence.

2. Moreover, the same learning rate does not apply to all parameter updates. If the training data is very sparse and the feature frequencies are very different, it should not be updated uniformly; instead, features that occur infrequently should use a larger update rate.

3. Another key challenge in neural networks when minimizing non-convex error functions is avoiding getting stuck in multiple other local minima. In fact, the problem does not stem from local minima, but from saddle points, which are points that incline in one dimension and decline in another. These saddle points are often surrounded by planes with the same error value, making it difficult for the SGD algorithm to escape, as the gradients approach zero in all dimensions.

Further Optimizations of Gradient Descent

Now we will discuss various algorithms used for further optimizing gradient descent.

1. Momentum

The high variance oscillation in the SGD method makes it difficult for the network to converge stably, so researchers proposed a technique called momentum, which accelerates SGD training by optimizing the training in relevant directions and dampening oscillations in irrelevant directions. In other words, this new method adds the component of the previous update vector ‘γ’ to the current update vector.

V(t)=γV(t−1)+η∇(θ).J(θ)

Finally, parameters are updated by θ=θ−V(t).

The momentum term γ is typically set to 0.9 or a similar value.

The momentum here is consistent with momentum in classical physics, just like throwing a ball from a hill, where the ball collects momentum as it falls, and its speed increases.

In the parameter update process, the principle is similar:

1) It enables the network to converge better and more stably;

2) It reduces the oscillation process.

When its gradient points in the actual direction of movement, the momentum term γ increases; when the gradient is opposite to the actual direction of movement, γ decreases. This means that the momentum term updates parameters only for relevant samples, reducing unnecessary parameter updates, thus achieving faster and more stable convergence, and reducing the oscillation process.

2. Nesterov Accelerated Gradient

A researcher named Yurii Nesterov pointed out a problem with the momentum method:

If a ball rolls down a slope blindly, it is very inappropriate. A smarter ball should be aware of where it is going; thus, when it encounters an upward slope again, the ball should slow down.

In fact, when the ball reaches the lowest point on the curve, the momentum is quite high. High momentum can cause it to completely miss the minimum, as the ball does not know when to slow down, thus continuing to move upward.

Yurii Nesterov published a paper in 1983 on solving the momentum problem, hence we call this method Nesterov Accelerated Gradient.

In this method, he proposed to take a large step based on previous momentum and then calculate the gradient for correction, thus achieving parameter updates. This pre-update method can prevent large oscillations, not missing the minimum, and is more sensitive to parameter updates.

Nesterov Accelerated Gradient (NAG) is a method that endows the momentum term with predictive capability, by using the momentum term γV(t−1) to modify the parameters θ. By calculating θ−γV(t−1), we obtain an approximate value of the parameters at the next position, where the parameters are a rough concept. Thus, we do not calculate the gradient value of the current parameter θ, but effectively predict the future based on the approximate future position of related parameters:

V(t)=γV(t−1)+η∇(θ)J(θ−γV(t−1)), then use θ=θ−V(t) to update parameters.

Now, by adapting the network updates to the slope of the error function, we can also accelerate SGD, adjusting and updating corresponding parameters according to their importance, to perform larger or smaller update amplitudes.

3. Adagrad Method

The Adagrad method adjusts the suitable learning rate η based on parameters, making large updates for sparse parameters and small updates for frequent parameters. Therefore, the Adagrad method is very suitable for handling sparse data.

In each time step, the Adagrad method calculates different learning rates for different parameters θ based on the past gradients.

Previously, each parameter θ(i) used the same learning rate, updating all parameters θ at each step. In each time step t, the Adagrad method selects different learning rates for each parameter θ, updates the corresponding parameters, and then vectorizes. For simplicity, let’s set the gradient of the loss function for parameter θ(i) at time t as g(t,i).

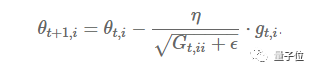
Figure 3: Parameter Update Formula

The Adagrad method modifies the corresponding learning rates η for each parameter θ(i) based on the previously calculated parameter gradients at each time step.

The main benefit of the Adagrad method is that it does not require manual adjustment of the learning rate. Most parameters use a default value of 0.01, remaining constant.

The main drawback of the Adagrad method is that the learning rate η constantly decreases and decays.

Since each additional term is positive, the cumulative sum of the squared gradient values in the denominator keeps growing during training. This, in turn, leads to a decrease in the learning rate, resulting in very small numbers, causing the model to completely stop learning and stop acquiring new additional knowledge.

As the learning speed decreases, the model’s learning capability rapidly diminishes, and the convergence speed is very slow, requiring long training and learning, i.e., learning speed degradation.

Another algorithm called Adadelta addresses the issue of this continuous decay of learning rates.

4. AdaDelta Method

This is an extension of Adagrad that aims to solve its learning rate decay problem. Adadelta does not accumulate all previous squared gradients; instead, it limits the accumulation of previous gradients to a fixed window size w.

Unlike the previous ineffective storage of w previous squared gradients, the sum of gradients is recursively defined as the exponentially decaying average of all previous squared gradients. Similar to the momentum term, the sliding average Eg² at time t depends solely on the previous average and the current gradient value.

Eg²=γ.Eg²+(1−γ).g²(t), where γ is set to a value close to the momentum term, about 0.9.

Δθ(t)=−η⋅g(t,i).

θ(t+1)=θ(t)+Δθ(t)

Figure 4: Final Parameter Update Formula

Another advantage of the AdaDelta method is that it no longer requires setting a default learning rate.

Improvements Made So Far

1) Calculated different learning rates for each parameter;

2) Also calculated the momentum term;

3) Prevented issues such as learning rate decay or gradient vanishing.

What Further Improvements Can Be Made?

In previous methods, the corresponding learning rates for each parameter were calculated, but why not calculate the corresponding momentum changes for each parameter and store them independently? This is the improvement point proposed by the Adam algorithm.

Adam Algorithm

The Adam algorithm stands for Adaptive Moment Estimation, which can calculate adaptive learning rates for each parameter. This method not only stores the exponentially decaying averages of the previous squared gradients of AdaDelta but also retains the exponentially decaying averages of the previous gradients M(t), similar to momentum:

M(t) is the first moment average of the gradient, and V(t) is the second moment non-central variance.

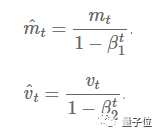
Figure 5: The Two Formulas Represent the First Moment Average and the Second Moment Variance of the Gradient

Thus, the final formula for parameter updates is:

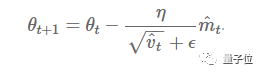
Figure 6: Final Formula for Parameter Updates

Where β1 is set to 0.9, β2 is set to 0.9999, and ϵ is set to 10-8.

In practical applications, the Adam method performs well. Compared to other adaptive learning rate algorithms, it converges faster and is more effective in learning, as well as correcting issues present in other optimization techniques, such as learning rate vanishing, slow convergence, or high variance parameter updates leading to significant fluctuations in the loss function.

Visualizing Optimization Algorithms

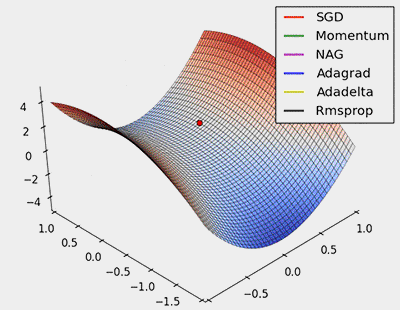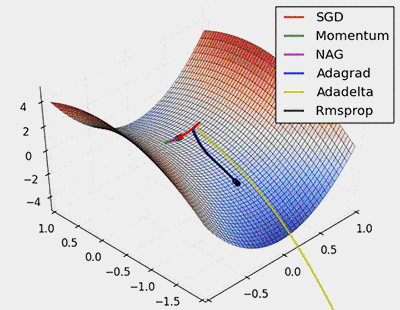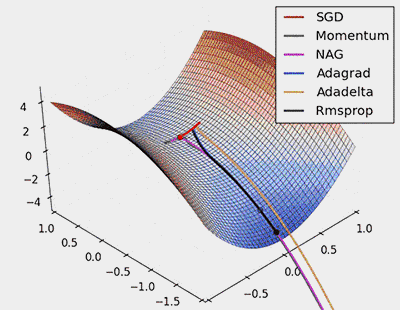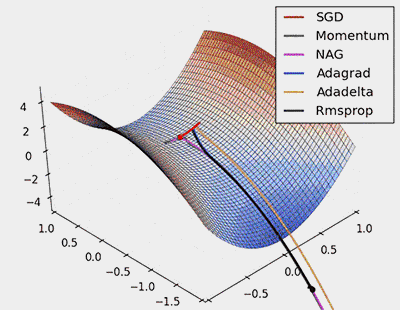
Figure 7: SGD Optimization of Saddle Points

From the above animation, it can be seen that adaptive algorithms can converge quickly and quickly find the correct target direction in parameter updates; while standard SGD, NAG, and momentum methods converge slowly and have difficulty finding the correct direction.

Conclusion

Which optimizer should we use?

When building neural network models, it is essential to select the best optimizer to ensure rapid convergence and accurate learning, while adjusting internal parameters to minimize the loss function to the greatest extent.

Adam performs well in practical applications, surpassing other adaptive techniques.

If the input dataset is relatively sparse, methods like SGD, NAG, and momentum may not perform well. Therefore, for sparse datasets, an adaptive learning rate method should be used, and another benefit is that it does not require manual adjustment of the learning rate; using default parameters can achieve optimal values.

If you want to make deep network model training converge quickly or if the neural network you build is complex, you should use Adam or other adaptive learning rate methods, as these methods are more effective in practice.

I hope this article helps you understand the differences in characteristics among different optimization algorithms.

From Gradient Descent to Adam: Understanding Neural Network Optimization Algorithms