This article is about 10,000 words long, and it is recommended to read for over 10 minutes.
This article introduces graph FMs and provides examples of their use.
Foundation models in language, vision, and audio have become one of the main research topics in machine learning for 2024, while FMs targeting graph-structured data are somewhat lagging behind. In this article, we argue that the era of graph FMs has begun and provide some examples of how to use them today.
What are Graph Foundation Models and How to Build Them?
Due to a certain degree of ambiguity regarding what constitutes a “foundation” model, it is appropriate to first define it to establish common ground:
“Graph foundation models are a single (neural) model that can learn transferable graph representations and can generalize to any new, previously unseen graph.”
One of the challenges is that graphs can take various forms and shapes, and their connections and feature structures can be quite different. Standard Graph Neural Networks (GNNs) are not considered “foundational” as they work best only on graphs with the same types and feature dimensions. Graph heuristic methods that can run on any graph (e.g., label propagation or personalized PageRank) also cannot be regarded as graph FMs because they do not involve any learning. While we appreciate large language models, it remains unclear whether parsing graphs into sequences that can be fed to LLMs (as in GraphText or Talk Like A Graph) is a suitable approach that preserves graph symmetry and scales to anything larger than toy-sized datasets (we will leave LLM + graph for a separate post).
The most important question in designing Graph FMs may be the transferable graph representation. As suggested by Mao, Chen, et al. in a recent ICML 2024 position paper LLMs can compress any text in any language into tokens from a fixed-size vocabulary. Video language FMs resort to patches that can always be extracted from images (RGB channels are always present in any image or video). It is currently unclear what a universal characterization (tokenization) scheme is for graphs that may have very diverse features, such as:
- A large graph with node features and some given node labels (typical for node classification tasks).
- A large graph without node features and categories but with meaningful edge types (typical for link prediction and KG reasoning).
-
Many small graphs with/without node/edge features, with graph-level labels (typical for graph classification and regression).
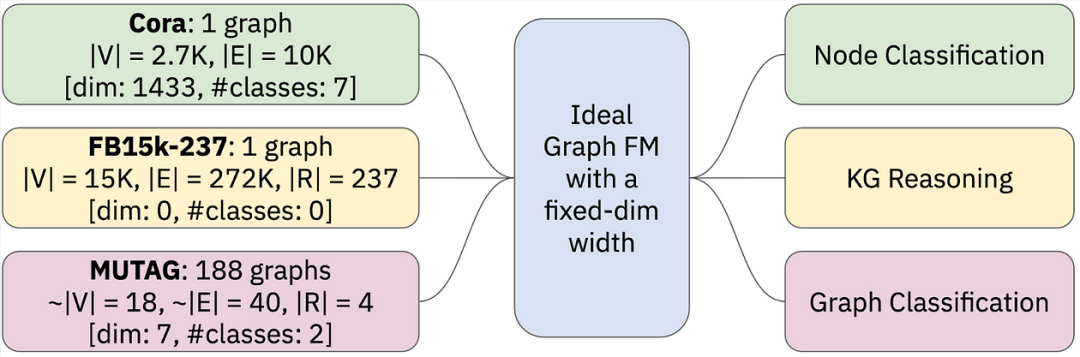
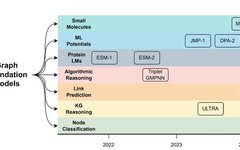
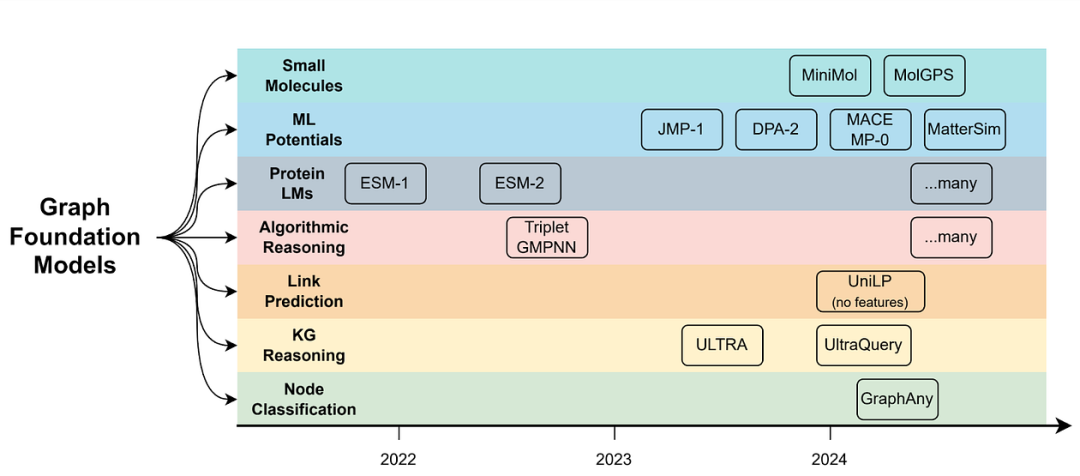
So far, the graph learning community still has several unresolved research questions when designing graph FMs:1️⃣ How to generalize in graphs with heterogeneous node/edge/graph features?For example, the popular Cora dataset for node classification is a graph with 1,433-dimensional node features, while the Citeseer dataset has 3,703-dimensional features. How to define a single representation space for such diverse graphs?2️⃣ How to promote in prediction tasks?Node classification tasks may have different numbers of node categories (e.g., Cora has 7 categories, while Citeseer has 6). Furthermore, can node classification models perform well in link prediction?3️⃣ What should the expressive capacity of foundation models be?There has been extensive research on the expressive capacity of GNNs, typically analogized with the Weisfeiler-Lehman isomorphism test. Since graph foundation models should ideally handle a wide range of problems, the correct expressive capacity is elusive. For example, in node classification tasks, node features are as important as graph homogeneity or heterogeneity. In link prediction, structural patterns and breaking self-isomorphism are more crucial (node features often do not yield significant performance improvements). In graph-level tasks, graph isomorphism begins to play a key role. In 3D geometric tasks like molecular generation, additional complexities due to continuous symmetry need to be addressed (see “A Guide to Geometric GNNs” ).In the following sections, we will show that at least in some tasks and domains, Graph FMs are already available. We will focus on their design choices regarding transferable characteristics and the practical advantages in inductive reasoning over new unseen graphs.📚 For more content, please refer to references [1][2] and the GitHub Repo Awesome_Graph_Foundation_Models.
Node Classification: GraphAny
For years, GNN-based node classifiers have been limited to single graph datasets. That is, for example, given a Cora graph with 2.7K nodes, 1433-dimensional features, and 7 classes, a GNN must be specifically trained on the Cora graph with its labels and run inference on the same graph. Applying the trained model to another graph (e.g., with 3703-dimensional features and 6 classes, Citeseer) would encounter insurmountable difficulties: how can a model generalize to different input feature dimensions and different numbers of classes? Typically, the prediction head is hardcoded to a fixed number of classes.To our knowledge, GraphAny is the first Graph FM where a single pre-trained model can perform node classification on any graph with any feature dimension and any number of classes. A single GraphAny model pre-trained on 120 nodes from the standard Wisconsin dataset successfully generalizes to over 30 other graphs of different sizes and features, and on average, its performance surpasses that of GCN and GAT GNN architectures trained from scratch on each graph.
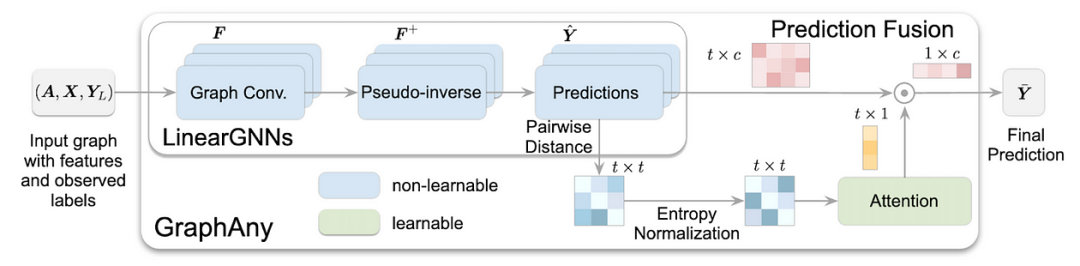
Setup: Semi-supervised node classification: Given graph G, node features X, and several labeled nodes from C classes, predict the labels of target nodes (binary or multi-class). The dimensionality of node features and the number of unique classes are not fixed and depend on the graph.Transferability: GraphAny does not model a universal latent space for all possible graphs (which is quite cumbersome, and may actually be impossible), but rather circumvents this issue by focusing on the interactions between spectral filter predictions. Given a set of high-pass and low-pass filters similar to simplified graph convolutions (e.g., operations in the form of AX and (IA)X, referred to as “LinearGNN” in the paper):0️⃣ GraphAny applies the filters to all nodes;1️⃣ GraphAny obtains the optimal weights for each predictor from nodes with known labels by solving a closed-form least squares optimization problem (optimal weights are represented as pseudo-inverse);2️⃣ The optimal weights are applied to unknown nodes to obtain tentative prediction logits;3️⃣ The pairwise distances between these logits are computed and entropy regularization is applied (so that different graphs and feature sizes do not affect the distribution). For example, for 5 LinearGNNs, this would yield 5 x 4 = 20 combinations of logits scores;4️⃣ Learn these logical inductive attention matrices to weight predictions most effectively (e.g., placing more attention on high-pass filters in heterogeneous graphs).Finally, the only learnable component in the model is the parameterization of attention (via MLP), which does not depend on the number of unique class targets but only on the number of LinearGNNs used. Similarly, all LinearGNN predictors are non-parametric, and their updated node features and optimal weights can be pre-computed for faster inference.📚 For more content, please refer to reference [3].
Link Prediction: Not Yet
Setup: Given a graph G, with or without node features, predict whether a link exists between a pair of nodes (v1, v2). For graphs with node features, we do not know of any single transferable model for link prediction. For non-featured graphs (or when you decide to deliberately omit node features), there is much to discuss – basically, all GNNs with labeling tricks may transfer to new graphs due to a unified node featureization strategy.It is well known that the biggest barrier in link prediction is the presence of self-isomorphic nodes (nodes with the same structural role) – standard GNNs assign them the same features, making it difficult to distinguish between the two links (v1, v2) and (v1, v3) in the diagram below. Double-radius node labeling or distance encoding are labeling tricks that disrupt self-isomorphic symmetry in node featureization.
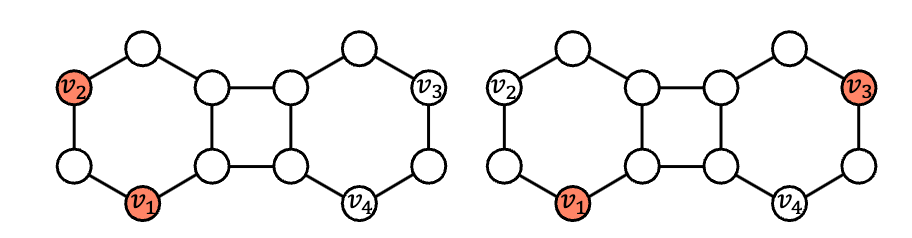
Perhaps the only way to use labeling tricks (for non-featured graphs) and evaluate on unseen graphs for link prediction is UniLP. UniLP is a context contrastive learning model that requires a set of positive and negative samples for each target link to predict. In practice, UniLP uses SEAL as the backbone GNN and learns attention on a fixed number of positive and negative samples. On the other hand, SEAL is very slow, so the first step to scale UniLP to large graphs is to replace subgraph mining with more efficient methods like ELPH and BUDDY .
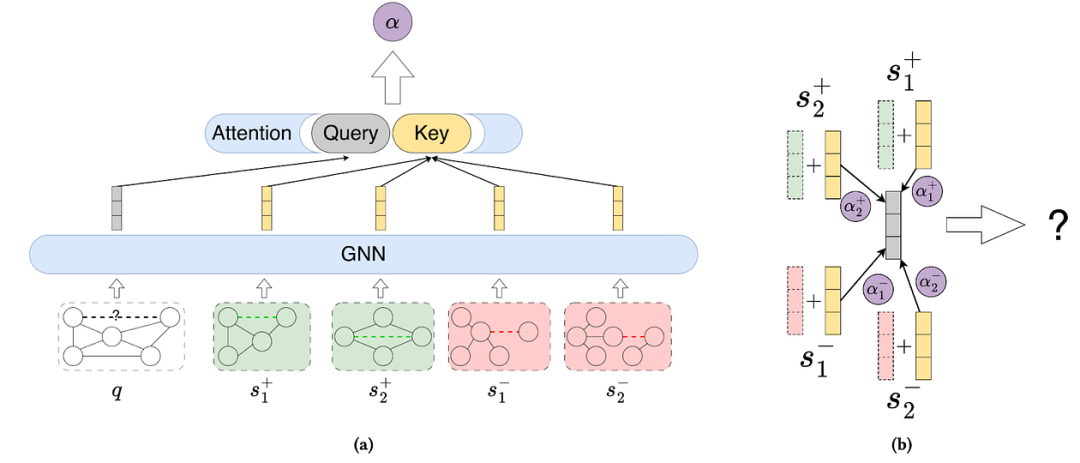
Transferable: The structural patterns learned by GNNs through labeling tricks – it turns out that methods like Neural Bellman-Ford can capture metrics for node pairs, such as personalized PageRank or Katz index (commonly used for link prediction).Now that we know how to handle self-isomorphism, the only step to achieve a single graph FM for link prediction is to add support for heterogeneous node features – perhaps a GraphAny-style approach could provide inspiration?📚 For more content, please refer to references [4][5][6][7].
Knowledge Graph Reasoning: ULTRA and UltraQuery
Knowledge graphs have sets of entities and relationships specific to the graph, such as common encyclopedic facts in Wikipedia/Wikidata or biomedical facts in Hetionet, which have different semantics and cannot be directly mapped to each other. For years, KG reasoning models have been hardcoded to a given relationship vocabulary, making them unable to transfer to new, unseen KGs with entirely new entities and relationships.ULTRA is the first KG reasoning foundation model that can transfer to any KG in a zero-shot manner during reasoning. That is, a single pre-trained model can perform reasoning on any multi-relational graph with any size and entity/relationship vocabulary. ULTRA’s average score exceeds 57 graphs, and its performance significantly outperforms baselines trained specifically on each graph. Recently, ULTRA has been extended to UltraQuery to support more complex logical queries involving conjunctions, disjunctions, and negation operators on graphs. UltraQuery can transfer to unseen graphs and over 10 complex query patterns on these unseen graphs, outperforming larger baselines trained from scratch.
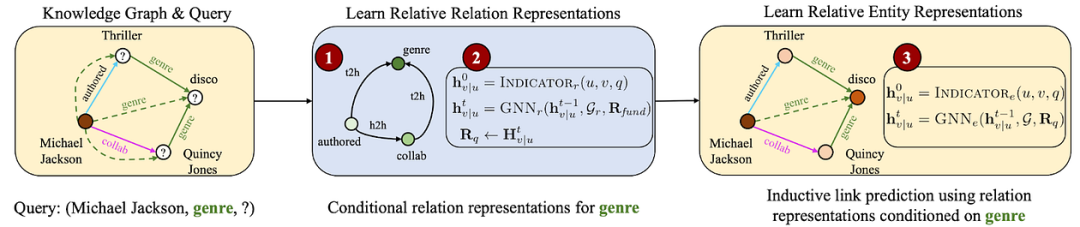
Setup: Given a multi-relational graph G with |E| nodes and |R| edge types, answer simple KG completion queries (head, relation, ?) or complex queries involving logical operators by returning the probability distribution of all nodes in the given graph. The sets of node and relationship types depend on the graph and may vary.Transferability: ULTRA relies on modeling relational interactions. Temporarily forgetting relationship identities and target graph domains, if we find that the “author” and “collaborator” relationships can share the same starting node, while the “student” and “co-author” relationships in another graph can also share the starting node, then the relative structural representations of these two pairs of relationships may be similar. This applies to any multi-relational graph in any domain, whether encyclopedic or biomedical KG. ULTRA goes further to capture four such “fundamental” interactions between relationships. These fundamental interactions can transfer to any KG (along with learned GNN weights) – thus, a pre-trained model can perform reasoning on any unseen graph and simple or complex reasoning queries.📚 For more content, please refer to references [8][9].
Algorithmic Reasoning: Generalist Algorithm Learner
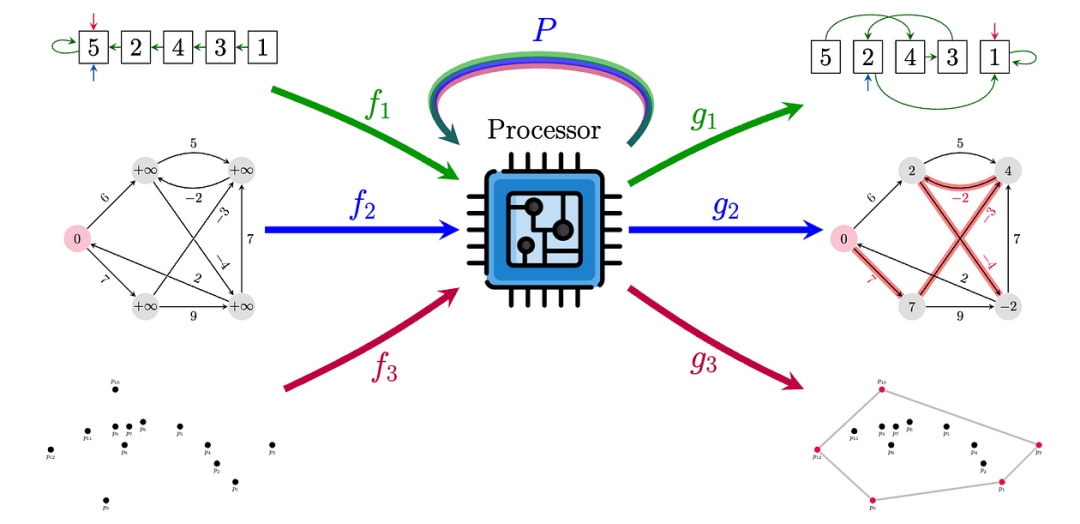
Setup: Neural Algorithm Reasoning (NAR) studies the execution of standard algorithms (e.g., sorting, searching, dynamic programming) in latent space and generalization to arbitrary size inputs. Many such algorithms can be represented with graphical inputs and pointers. Given a graph G with node and edge features, the task is to simulate the algorithm and produce the correct output. Alternatively, you can access prompts – time series of intermediate states of the algorithm, which can serve as intermediate supervision signals. Clearly, different algorithms require performing different numbers of steps, so the length here is not fixed.Transferability: Homogeneous feature spaces of similar algorithms and similar control flows. For example, Prim’s algorithm and Dijkstra’s algorithm have similar structures, differing only in the choice of key functions and edge relaxation subroutines. Moreover, there is evidence indicating a direct connection between message passing and dynamic programming. This is the main motivation for the “processor” neural network, which can update the latent states of all considered algorithms (30 classic algorithms from the CLRS book ).Triplet-GMPNN is the first such generalist processor neural network (by 2024, it has become quite a standard neural network in the NAR literature) – it is a GNN that operates on node triplets and their features (similar to Edge Transformers in AlphaFold and triangular attention). This model is trained in a multitask mode on all algorithmic tasks in benchmark tests and employs various optimizations and tricks. Compared to single-task expert models, a single model improves the average performance across 30 tasks by over 20% (in absolute numbers).Nevertheless, both the encoder and decoder are specifically parameterized for each task – one way to unify input and output formats might be to use text from LLM processors, as done in the recent CLRS text version .
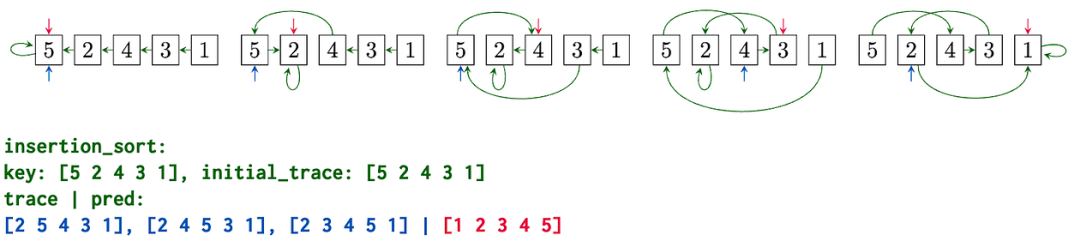
Perhaps the most interesting question in NAR for 2024 and 2025 is:
Can the algorithmic reasoning ideas of OOD generalization become the key to generalizable LLM reasoning?
It is well known that LLMs struggle with complex reasoning problems, with dozens of papers appearing monthly on arXiv attempting a new prompting method to improve benchmark performance by one or two percentage points, yet most papers fail to transfer between tasks with similar graph structures (see examples below). We need more principled approaches, and NAR has the potential to fill this gap!

📚 For more content, please refer to references [10][11].
Geometric and AI4Science Foundation Models
In the fields of geometric deep learning and scientific applications, foundation models are gradually becoming universal ML potentials, protein language models, and universal molecular property predictors. Although there exists a common vocabulary in most cases (e.g., atomic types in small molecules or amino acids in proteins), and we do not have to consider universal featureization, the main complexity lies in the physical properties of atomic objects in the real world – they exhibit distinct 3D structures and properties (such as energy), which theoretical bases are rooted in chemistry, physics, and quantum mechanics.
ML Potential: JMP-1, DPA-2 for Molecules, MACE-MP-0 for Inorganic Crystals, and MatterSim
Setup: Given a 3D structure, predict the energy of the structure and the forces on each atom;What is transferable: atomic vocabulary from the periodic table.ML potentials estimate the potential energy of compounds (such as molecules or periodic crystals) based on their 3D coordinates and optional inputs (like periodic boundary conditions of crystals). For any atomic model, the possible atomic vocabulary is always constrained by the periodic table, which currently includes 118 elements. The “foundation” aspect of ML potentials is the ability to generalize to any atomic structure (which can have various combinations) and be stable enough for molecular dynamics (MD), drug discovery, and material discovery processes.Roughly around the same time, JMP-1 and DPA-2 aim to become such universal ML potential models – they are trained on a wide variety of structures – from organic molecules to crystals to MD trajectories. For instance, a single pre-trained JMP-1 performs excellently on QM9, small molecule rMD17, crystal MatBench and QMOF, and large molecule MD22, SPICE, matching or exceeding specialized dataset models. Similarly, MACE-MP-0 and MatterSim are state-of-the-art inorganic crystal FMs (MACE-MP-0 has already provided weights), evaluated on over 20 crystal tasks, from multi-component alloys to combustion and molten salts. Equivariant GNNs are at the core of these systems, helping to process equivariant features (Cartesian coordinates) and invariant features (such as atomic types).
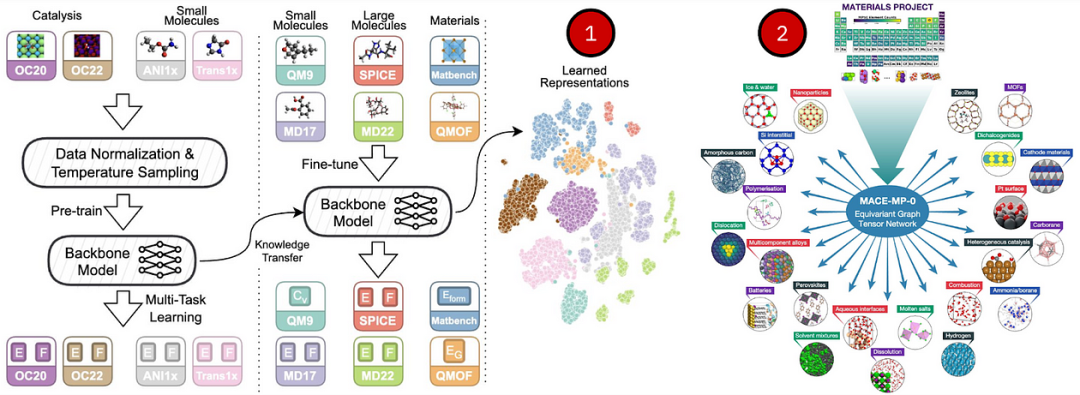
The next frontier seems to be machine learning accelerated molecular dynamics simulations – traditional computational methods operate on the femtosecond scale (10-15) and require millions and billions of steps to simulate molecules, crystals, or proteins. Accelerating such computations would have a tremendous scientific impact.📚 For more content, please refer to references [12][13][14][15].
Protein LM: ESM-2
Setup: Given a protein sequence, predict masked tokens similar to masked language modeling;Transferable vocabulary: 20 (22) amino acids.Protein sequences are similar to natural language with amino acids as tokens, and Transformers excel at encoding sequential data. Although the vocabulary of amino acids is relatively small, the potential protein space is enormous, thus training on a large number of known proteins may imply properties of unseen combinations. Due to the large amount of pre-training data, various available checkpoints, and informative features, ESM-2 may be the most popular protein LM.
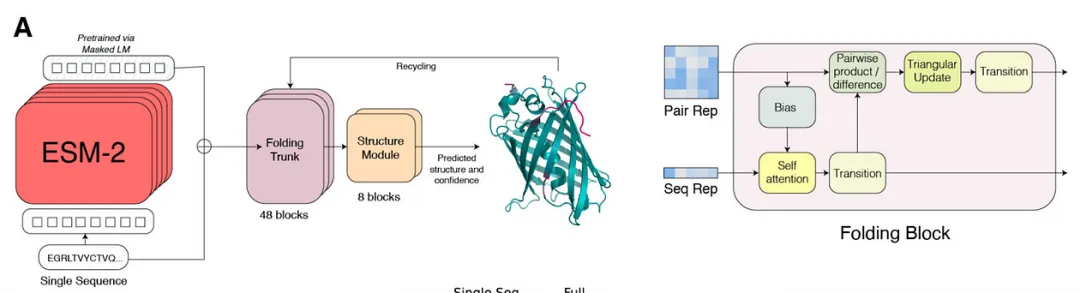
📚 For more content, please refer to references [16][17].
2D Molecules: MiniMol and MolGPS
Setup: Given a 2D graphical structure with atomic types and bond types, predict molecular properties.What is transferable: atomic and bond types vocabulary from the periodic table.For 2D graphs (without 3D atomic coordinates), general encoding and transferability come from a fixed vocabulary of atomic and bond types, which can be fed into any GNN or Transformer encoder. Although molecular fingerprints (Morgan fingerprints ) have been used since the 1960s, their main goal is to evaluate similarity rather than model potential space. Recent examples of universal models for learning molecular representations include MiniMol and MolGPS , which have been trained on large molecular graph corpora and explored across dozens of downstream tasks. That is to say, you still need to fine-tune separate task-specific decoders/predictors based on the model’s representations – in this sense, a pre-trained model will not run zero-shot inference on all possible unseen tasks but will run zero-shot inference on tasks the decoder has been trained on. However, fine-tuning remains a good cheap option, as these models are several orders of magnitude smaller than LLMs.

📚 For more content, please refer to references [19][20].
Expressiveness and Scaling Laws: Can Graph FMs Scale?
Transformers in LLMs and multimodal boundary models are quite standard, and we know some basic principles of their expansion. Are Transformers (as an architecture, not LLMs) equally effective on graphs? What are the general challenges faced when designing backbones for Graph FMs?If we classify the models highlighted above, only two fields have transformers – protein LMs (ESM) and small molecules (MolGPS). The rest are GNNs. The reasons are as follows:
-
Vanilla Transformers cannot scale to reasonably large graphs larger than the standard context length (>4-10k nodes). Any situation beyond this range requires tricks, such as providing only subgraphs (losing the entire graph structure and long-distance dependencies) or linear attention (which may not have good scalability). In contrast, GNNs are linear in edge count and, in sparse graphs (V ~ E), linear in node count.
-
The expressive capacity of Vanilla Transformers without position encoding is less than that of GNNs . Mining position encodings like Laplacian PE on a graph with V nodes is O(V³).
- When encoding graphs through transformers, what should “tokens” be? There is no clear winner in the literature, for example, nodes , node + edge , or subgraphs are all viable options.
➡️ When it comes to expressiveness, different graph tasks require handling different symmetries, for instance, self-isomorphic nodes in link prediction lead to indistinguishable representations, while in graph classification/regression, going beyond 1-WL is necessary to distinguish molecules, or otherwise these molecules may appear isomorphic to the original GNN.
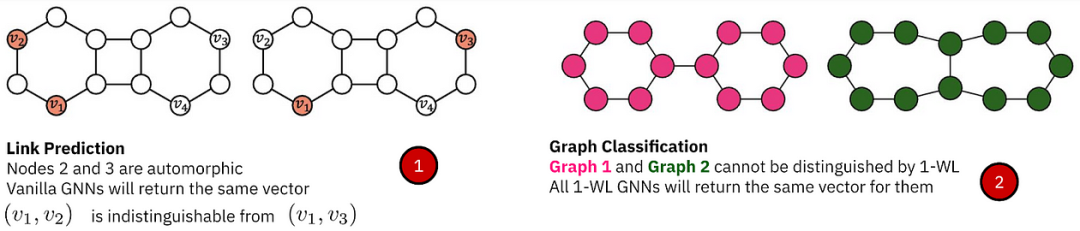
This fact raises two questions:
How powerful should GFM be? What is the trade-off between expressiveness and scalability?
Ideally, we want a single model to excel at solving all these symmetry problems equally well. However, a more expressive model will lead to higher computational costs in architecture for training and inference. We agree with the recent ICML’24 position paper on the future directions of Graph ML theory that the community should seek a balance between expressiveness, generalization, and optimization.However, it is worth noting that as the availability of training data continues to increase, delaying the direct learning of complex symmetries and invariances from data (rather than baking them into the model) may be a computationally cheaper idea. Several recent good examples are AlphaFold 3 and Molecular Conformer Fields , which achieve SOTA in many generative applications without expensive equivariant geometric encoders.📚 For more content, please refer to references [21].➡️ When it comes to scaling, both models and data should scale. However:❌ Non-geometric graphs: Currently, there is no principled research on scaling GNNs or Transformers to large graphs and common tasks (like node classification and link prediction). 2-layer GraphSAGE is often not far from huge 16-layer graph Transformers. A similar trend is seen in KG reasoning, where a ULTRA model with fewer than 200k parameters (as mentioned above) outperforms shallow embedding models with millions of size across over 50 graphs. Why is this? We hypothesize the key lies in 1️⃣ Task nature – most non-geometric graphs are noise similarity graphs, unconstrained by specific physical phenomena like molecules, 2️⃣ Given rich node and edge features, the model must learn representations of graph structures (commonly used in link prediction) or merely be a function of given features (a good example is node classification in OGB , where most gains are achieved by adding LLM feature encoders).✅ Geometric graphs: Recently, several studies have focused on molecular graphs:
-
Frey et al. (2023) studied the scaling of geometric GNNs for ML potential;
-
Sypetkowski, Wenkel et al. (2024) introduced MolGPS and studied scaling MPNNs and Graph Transformers to 1 billion parameters on large datasets of 5 million molecules;
- Liu et al. (2024) probed GCNs, GINs, and GraphGPS with up to 100 million parameters on molecular datasets with up to 4 million molecules.
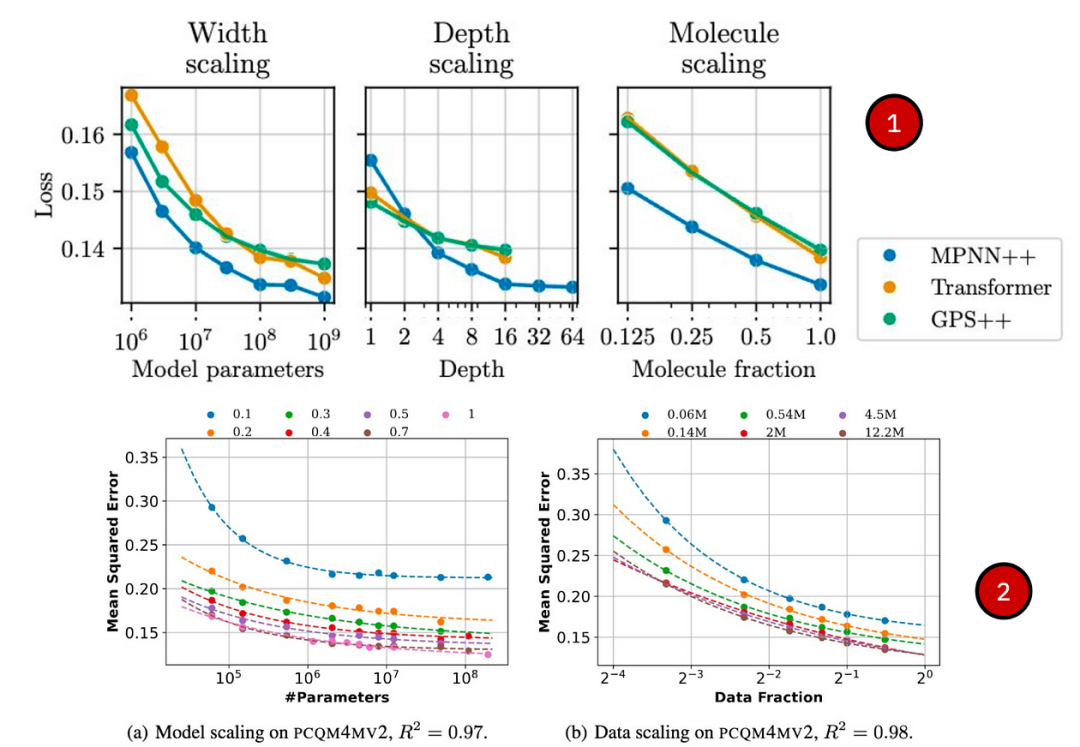
Data Issues: What Should Scale? Is There Enough Graph Data to Train Graph FMs?
1️⃣ What should scale in graph data? Nodes? Edges? Number of graphs? Is there anything else?There is no clear winner in the literature; we prefer to use the broader term diversity, i.e., pattern diversity in graph data. For instance, in node classification on large product graphs, it may not make much difference whether you train on a graph with 100 million nodes or 10 billion nodes, as it is similar to the nature of user-item graphs. However, showcasing examples of homogeneity and heterogeneity across different scales and sparsity may be very beneficial. In GraphAny, demonstrating such examples can build a robust node classifier that generalizes to different graph distributions; when using ULTRA for KG reasoning, it was found that the diversity of relational patterns in pre-training had the most significant impact on inductive generalization, for example, a large dense graph performs worse than a set of smaller but sparse, dense, few-relational, and multi-relational graphs.In molecular graph-level tasks, for example, in MolGPS, scaling the number of unique molecules with different physical properties is very beneficial (as shown in the above figure).Moreover, UniAug found that the higher the coverage of structural patterns in pre-training data, the better the performance across different downstream tasks in various domains.2️⃣ Is there enough data to train Graph FMs?Publicly available graph data is several orders of magnitude smaller than natural language tokens, images, or videos, and there is no problem with that. This article contains thousands of language and image tokens, but no explicit graphs (unless you try to parse this text into a graph resembling Abstract Meaning Representation ). The number of “good” proteins with known structures in the PDB is very few, and the number of known “good” drug molecules is also very few.
Are graph FMs doomed to fail due to data scarcity?
Not necessarily. Two feasible paths are: (1) more efficient sampling architectures; (2) using more black-box and synthetic data.GraphWorld and other synthetic benchmarks may help increase the diversity of training data and improve generalization to real-world datasets. Conversely, black-box data obtained from scientific experiments is likely to be a key factor in building successful foundation models in AI 4 Science – those who master it will have an advantage in the market.📚 For more content, please refer to references [20][22][23].
Key Takeaways
➡️ How to generalize across graphs with heterogeneous node/edge/graph features?
-
Non-geometric graphs: relative information transfer (e.g., prediction differences in GraphAny or relational interactions in Ultra), while absolute information does not transfer.
- Geometric graphs: transfer becomes easier due to the fixed set of atoms, but models must learn some physical concepts to be reliable.
➡️ How to generalize in prediction tasks?
-
So far, there has not been a single model (in non-geometric GNNs) capable of performing node classification, link prediction, and graph classification in zero-shot inference mode.
- Building all tasks from a single perspective may help, for example, node classification can be constructed as link prediction.
➡️ What is the optimal model expressiveness?
-
Node classification, link prediction, and graph classification leverage different symmetries.
-
Maximizing expressiveness of models will quickly lead to exponential runtime complexity or huge memory costs – a balance between expressiveness and efficiency needs to be maintained.
- The relationship between expressiveness, sample complexity (how much training data is needed), and inductive generalization is still unknown.
➡️ Data
-
Publicly available graph data is several orders of magnitude smaller than text/visual data, and models must be sample efficient.
-
Scaling laws are in an emerging stage; it is unclear what to scale – node counts? Edges? Motifs? What is the concept of tokens in graphs?
- Geometric GNNs: more experimental data is available, which may not mean much to domain experts but could be valuable for neural networks.
- Mao, Chen, et al. Graph Foundation Models Are Already Here. ICML 2024
- Morris et al. Future Directions in Foundations of Graph Machine Learning. ICML 2024
- Zhao et al. GraphAny: A Foundation Model for Node Classification on Any Graph. Arxiv 2024. Code on Github
- Dong et al. Universal Link Predictor By In-Context Learning on Graphs, arxiv 2024
- Zhang et al. Labeling Trick: A Theory of Using Graph Neural Networks for Multi-Node Representation Learning. NeurIPS 2021
- Chamberlain, Shirobokov, et al. Graph Neural Networks for Link Prediction with Subgraph Sketching. ICLR 2023
- Zhu et al. Neural Bellman-Ford Networks: A General Graph Neural Network Framework for Link Prediction. NeurIPS 2021
- Galkin et al. Towards Foundation Models for Knowledge Graph Reasoning. ICLR 2024
- Galkin et al. Zero-shot Logical Query Reasoning on any Knowledge Graph. arxiv 2024. Code on Github
- Ibarz et al. A Generalist Neural Algorithmic Learner LoG 2022
- Markeeva, McLeish, Ibarz, et al. The CLRS-Text Algorithmic Reasoning Language Benchmark. arxiv 2024
- Shoghi et al. From Molecules to Materials: Pre-training Large Generalizable Models for Atomic Property Prediction. ICLR 2024
- Zhang, Liu et al. DPA-2: Towards a universal large atomic model for molecular and material simulation, arxiv 2023
- Batatia et al. A foundation model for atomistic materials chemistry, arxiv 2024
- Yang et al. MatterSim: A Deep Learning Atomistic Model Across Elements, Temperatures and Pressures, arxiv 2024
- Rives et al. Biological Structure and Function Emerge from Scaling Unsupervised Learning to 250 Million Protein Sequences. PNAS 2021
- Lin, Akin, Rao, Hie, et al. Language models of protein sequences at the scale of evolution enable accurate structure prediction. Science 2023. Code
- Morgan HL (1965) The generation of a unique machine description for chemical structures — a technique developed at chemical abstracts service. J Chem Doc 5:107–113
- Kläser, Banaszewski, et al. MiniMol: A Parameter Efficient Foundation Model for Molecular Learning, arxiv 2024
- Sypetkowski, Wenkel et al. On the Scalability of GNNs for Molecular Graphs, arxiv 2024
- Morris et al. Future Directions in Foundations of Graph Machine Learning. ICML 2024
- Liu et al. Neural Scaling Laws on Graphs, arxiv 2024
- Frey et al. Neural scaling of deep chemical models, Nature Machine Intelligence 2023
Editor: Huang Jiyuan
About Us
Data Pie THU, as a public account on data science, backed by the Tsinghua University Big Data Research Center, shares the latest research dynamics in data science and big data technology innovation, continuously disseminating knowledge of data science, striving to build a talent aggregation platform for data, and creating the strongest group in China’s big data.

Sina Weibo: @Data Pie THU
WeChat Video Number: Data Pie THU
Today’s Headlines: Data Pie THU