First Review on Multimodal Trajectory Prediction

Trajectory prediction is a critical task for providing safe and intelligent behavior for autonomous systems. Over the years, many cutting-edge methods have been proposed to improve spatial and temporal feature extraction. However, human behavior is inherently multimodal and uncertain: given past trajectories and surrounding environmental information, agents can have multiple possible future trajectories. To address this issue, a fundamental task known as Multimodal Trajectory Prediction (MTP) has recently been studied, which aims to generate diverse, acceptable, and interpretable future prediction distributions for each agent. This article serves as the first review of MTP, providing a unique taxonomy and comprehensive analysis of frameworks, datasets, and evaluation metrics. Additionally, this paper discusses several future directions that can help researchers propose new multimodal trajectory prediction systems.

1 Introduction

Over the years, trajectory prediction has garnered significant attention in autonomous systems such as social robots and self-driving cars. It aims to predict the future trajectories of road users, such as vehicles, pedestrians, and cyclists, based on past trajectories and surrounding environments (including static factors like terrain and obstacles, as well as dynamic factors like surrounding moving agents).

Traditional trajectory prediction explores physical models to simulate human behavior, using physical models to predict future motion, such as social forces [Helbing and Molnár, 1995], which describe social behaviors like gathering and collision avoidance as attractive and repulsive forces. However, such models struggle with complex interactions, and their predictions are not human-like. Recently, learning-based models have been proposed that utilize advanced modules to learn complex spatial and temporal interactions from datasets, such as pooling [Alahi et al., 2016], attention [Gupta et al., 2018], and graph neural networks [Mohamed et al., 2020; Huang et al., 2019].

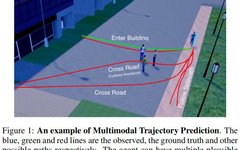
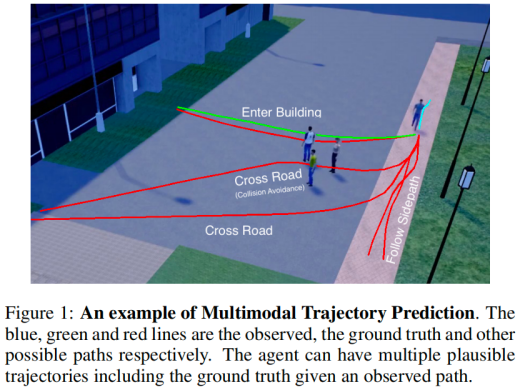
Trajectory prediction is often framed as a Deterministic Trajectory Prediction (DTP) task, where the model provides only one prediction for each agent. However, DTP is severely impacted by the uncertainty of limited social cues, and its performance is often constrained. For example, in Figure 1, suppose an agent is about to enter a building, and the observed path indicates that it could also cross the street or walk on the sidewalk. Since all scenarios are reasonable, it is unrealistic for DTP to predict a single trajectory without sufficient cues (such as human intent).

Therefore, Gupta et al. [2018] proposed a task called Multimodal Trajectory Prediction (MTP), where the model can provide multiple predictions to encompass all modes of future trajectories, i.e., possible paths. MTP can handle the uncertainty of predictions and has become the default setting in nearly all recent studies. Some methods focus on improving feature extraction modules, while others attempt to generate a more diverse and socially acceptable distribution using only one ground truth future trajectory.

This paper presents the first review of multimodal trajectory prediction. Existing reviews on pedestrian trajectory prediction [Rudenko et al., 2020] and vehicle trajectory prediction [Teeti et al., 2022] have constructed their taxonomies from the perspective of feature extraction, briefly introducing MTP as auxiliary content. As a more realistic scenario in trajectory prediction, we believe a deeper investigation and analysis are necessary. This paper provides a taxonomy of MTP frameworks, datasets, and evaluation metrics, analyzing their advantages and issues. It then discusses potential directions that should become the focus of future research.

2 Background

Agents

Agents in trajectory prediction are road users with self-awareness, such as pedestrians, drivers, or cyclists.

Trajectories

The trajectory of agents in trajectory prediction is defined as a sequence of two-dimensional real-world or pixel coordinates: where is the timestamp observed trajectory, is the ground truth of the time step, and is the index of the scene’s agents. All contain 2D indices.

Trajectory Prediction

The goal of trajectory prediction is to optimize the model to predict future trajectories using observed information as input:

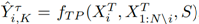
where is the adjacent observed trajectory of the agent, and is the scene information, such as radar data, high-definition maps, scene graphs, etc. At that time, each agent is allowed to make only one prediction, and the task is to determine the trajectory prediction (DTP) and minimize the expected prediction error compared to the ground truth. Otherwise, it becomes Multimodal Trajectory Prediction (MTP), which aims to predict the distribution of all acceptable future trajectories.

DTP Standard Framework

The DTP framework typically follows the sequence-to-sequence structure shown in Figure 3a, where past encoding extracts spatial and temporal information from observed data, and the decoder predicts future paths. To construct a DTP model, past encoding can be a combination of (1) encoding modules for temporal, social, and physical features [Xue et al., 2018; Sadeghian et al., 2019; Dendorfer et al., 2021]; (2) CNN-based raster high-definition maps [Wang et al., 2020] or heat maps [Mangalam et al., 2021]; or (3) graph neural network-based vectorized high-definition map encoding modules [Gao et al., 2020]. The decoder can be an autoregressive module based on recurrent networks, or a non-autoregressive module based on MLP or CNN. Reconstruction loss (e.g., l1 or l2 loss) is used to optimize predictions to achieve minimal error between expected predictions and the ground truth. MTP models can also utilize these past encodings and decodings within their frameworks, except their decoding is executed repeatedly with different feature inputs.

Multimodality in Trajectory Prediction

Given the observed information, there can be multiple reasonable and socially acceptable future predictions for an agent. Thus, it differs from data modalities in other multimodal learning tasks. Due to the limited cues available from the environment and the inherent randomness of each motion, it is unlikely that the model can predict a future trajectory that consistently and accurately matches the ground truth. Therefore, MTP requires the model to provide multiple trajectories that are acceptable to humans.

3 MTP Framework

The “good” distribution predicted from the MTP model should meet several aspects:

1. Diversity, where the predicted distribution should cover all possible solutions;
2. Social acceptability, where the predicted paths should conform to past trajectories and follow social norms;
3. Interpretability/controllability, where each prediction should follow reasonable intentions or be controlled by understandable conditions.

This is challenging because the optimal distribution is estimated using only one ground truth trajectory, which often leads to a lack of diversity and acceptability in predictions. To address this issue, many advanced frameworks have been proposed. In this section, we review the MTP frameworks and their classification in Figure 2 and the general process in Figure 3.

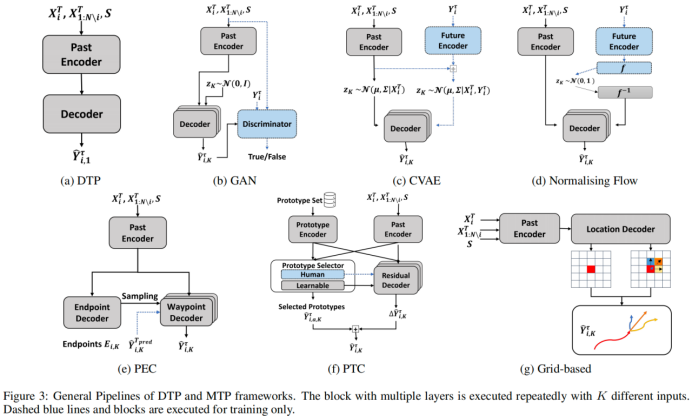
3.1 Noise-Based MTP Framework

The simplest way to convert DTP to MTP is to inject random noise into the model. This section will discuss the noise-based MTP framework introduced by Gupta et al. [2018]. Features from the past encoder are concatenated with a Gaussian noise vector and sent to the decoder for different predictions. The predictions are optimized using variety loss through minimal reconstruction error:

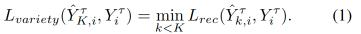
As described by Gupta et al. [2018], variety loss can successfully mitigate the mode collapse problem caused by reconstruction loss. Thiede and Brahma [2019] explain that learners trained with variety loss can converge to the square root of the ground truth probability density function, further demonstrating the success of this loss function.

This framework can be easily integrated into any DTP model and has been widely used in trajectory prediction. However, this framework may produce unrealistic predictions and be difficult to control. To address this issue, many advanced generative frameworks have been proposed.

Generative Adversarial Networks (GAN)

To obtain high-quality predictions, a special loss function is needed to distinguish bad predictions from good ones, known as adversarial loss. Gupta et al. [2018] introduced the GAN-based MTP framework and its first model S-GAN. The general process is shown in Figure 3b, where a discriminator is learned to classify whether future trajectories are real or predicted, and the adversarial loss is its cross-entropy result. Further work aims to use more advanced GAN frameworks to improve performance. For example, Kosaraju et al. [2019] proposed Social-BiGAT, which performs reversible transformations between its latent noise vector in each generation to further mitigate mode collapse. Meanwhile, Amirian et al. [2019] claim that reconstruction loss is a major factor leading to mode collapse. Therefore, their model S-Way diminishes this loss and follows InfoGAN to use latent encoding to control predictions. Dendorfer et al. [2021] show that the manifold of future path distributions has become discontinuous, so other GAN-based methods may not cover well. Therefore, they proposed MG-GAN, which uses multiple decoders, each handling a continuous sub-manifold.

Conditional Variational Autoencoders (CVAE)

CVAE-based trajectory prediction models [Lee et al., 2017; Yuan et al., 2021; Chen et al., 2021] follow [Sohn et al., 2015] to maximize the evidence lower bound of feature distributions, as shown in Figure 3c, as an alternative to obtain diverse predictions. Additionally, CVAE can better control and enhance its latent distribution. For example, Dis-Dis [Chen et al., 2021] and ABC [Halawa et al., 2022] predict personalized and action-known motion patterns by distinguishing feature distributions through contrastive learning. A recent model named SocialVAE [Xu et al., 2022] applies CVAE with recurrent networks to utilize the temporal dimension of CVAE. This paper strongly recommends [Ivanovic et al., 2021] for a comprehensive overview of CVAE in trajectory prediction.

Normalizing Flows (NF)

Due to implicit distribution modeling, GAN or CVAE-based models are challenging to train. Therefore, the NF-based MTP framework has been proposed to explicitly learn data distributions through reversible networks, as shown in Figure 3d, which can transform complex distributions into manageable forms via reversible transformations. For instance, HBAFlow [Bhattacharyya et al., 2021] uses a Haar wavelet-based block autoregressive model that splits coupling to learn the distribution of motion predictions, while FloMo [Schöoller and Knoll, 2021] employs monotonic rational quadratic splines for representation and rapid inversion. STGlow [Liang et al., 2022] proposes generative flows with mode normalization to learn motion behaviors conditioned on social interactions. However, no NF-based model has been able to handle discontinuous manifolds. A seemingly reasonable solution is to mimic MG-GAN using multiple reversible decoders.

3.2 Anchor Conditional MTP Framework

To effectively guide the model in predicting trajectories with controlled behavior, it has been proposed that each prediction should be conditioned on prior knowledge [Chai et al., 2020; Zhao et al., 2021], also named anchors, which are explicit for each mode. Well-known anchors include endpoints, the final positions that agents might reach, or prototype trajectories, the basic actions agents might follow. Ideally, using anchors can effectively alleviate the mode collapse problem and yield more robust and interpretable predictions. This paper classifies the framework using anchors as the anchor conditional MTP framework. This framework generally includes two sub-tasks: (1) anchor selection, selecting K possible anchors from the anchor set; (2) waypoint encoding, predicting waypoints based on the given anchors, ultimately predicting future trajectories. Anchor selection can be done through random sampling or top K ranking. The “best” anchor is then selected as a guiding force during training to optimize waypoint decoding [Williams and Zipser, 1989]. In this section, two derivative frameworks are discussed, using endpoints and prototype trajectories as anchors, referred to as the Predictive Endpoint Conditional (PEC) and Prototype Trajectory Conditional (PTC) frameworks, respectively.

Predictive Endpoint Conditional (PEC) Framework

Intuitively, agents can first decide where they will arrive and then plan their future trajectories [Rehder and Kloeden, 2015]. This introduces the PEC framework, where endpoints can be predicted as anchors, and path points are generated to reach these positions. As shown in Figure 3e, this framework first predicts the endpoint distribution through an endpoint decoder. Then, the path point decoder predicts intermediate positions given each selected endpoint. During training, real endpoints are selected to enhance the relationship between predicted path points and the conditioned endpoints. During testing, endpoints are selected by randomly sampling from the heatmap or from the top K. The PEC framework is widely used in current trajectory prediction methods due to its simplicity and effectiveness.

Mangalam et al. [2020] first introduced the PEC framework and proposed PECNet, which generates multiple endpoints using CVAE. Further methods indicate that if predictions can be controlled by scene-compliant endpoints, the model can achieve better performance. For example, TNT [Zhao et al., 2021] and DenseTNT [Gu et al., 2021] predict vehicle endpoints by sampling the positions of lane centerlines, while YNet [Mangalam et al., 2021] and Goal-GAN [Dendorfer et al., 2020] directly predict endpoint heatmaps by integrating observed trajectories and scene segmentation images. Meanwhile, ExpertTraj [Zhao and Wildes, 2021] suggests that endpoints can be sampled from existing trajectory repositories with minimal dynamic time transformation differences. Additionally, PEC framework work can assist in long-term predictions by adjusting endpoints and intermediate path points [Mangalam et al., 2021; Wang et al., 2022]. Tran et al. [2021] estimate the destination of agents leaving the observation area to better control future trajectories within the dynamic prediction range. Future PEC models can focus on avoiding unreachable endpoints due to intermediate obstacles and utilize multimodality of path points to the same endpoint.

Prototype Trajectory Conditional (PTC) Framework

The anchor set of the PTC framework consists of prototype trajectories, where each trajectory represents a mode and provides the basic motion that path points should follow and necessary improvements. As shown in Figure 3f, the PTC framework learns to select candidate prototype trajectories from the anchor set and predicts their residuals to the ground truth during the path point decoding phase via a residual decoder. To construct an anchor set with sufficient diversity, k-means clustering can be used on trajectories from existing datasets in MultiPath [Chai et al., 2020], and a greedy approximation algorithm in CoverNet [Phan-Minh et al., 2020]. Additionally, S-Anchor [Kothari et al., 2021] constructs a set with different speeds and directions through discrete selection models [Antonini et al., 2006] to integrate social interactions. SIT [Shi et al., 2022] builds a tree-like roadmap and dynamically selects and refines path segments. Clearly, using prototype trajectories can simplify training and achieve diversity. However, current prototype trajectories are often too simplistic to handle complex scenarios. Therefore, future work can explore more advanced prototype trajectories.

3.3 Grid-Based MTP Framework

The grid-based MTP framework is an alternative approach that uses occupancy grid maps to indicate where agents will arrive in the next time step. As shown in Figure 3g, the scene is divided into grid cells, and the model predicts the occupancy probability in each cell, determined by the observed information for each time step. Multimodal predictions can be obtained through precise decision sampling for the next position in TDOR [Guo et al., 2022] using Gumbel Softmax, or searching for trajectories with the top K cumulative log probabilities in Multiverse [Liang et al., 2020] and ST-MR [Li et al., 2022]. The main advantage of grid-based frameworks is their high compatibility with advanced training strategies (e.g., reinforcement learning or occupancy loss) and their suitability for long-term predictions. However, due to the extensive computation of convolution operations and high sensitivity to map resolution, they are rarely used.

3.4 Bivariate Gaussian for Output Representation

Some models do not regress precise two-dimensional coordinates but assume a bivariate Gaussian distribution for the position at each time step. The goal of these models is to maximize the likelihood of the ground truth in the predicted distribution through negative log-likelihood loss. This strategy was first used for deterministic predictions in S-LSTM [Alahi et al., 2016], but was replaced by GAN-based models due to its non-differentiable position sampling. It was then reused in Social STGCNN [Mohamed et al., 2020] and [Shi et al., 2021] for MTP, where multiple trajectories can be obtained by sampling K future positions from the predicted distribution.

However, the output positions are sampled individually, which may be temporally uncorrelated, leading to unrealistic predictions. One solution is to integrate it with recurrent neural networks as a special grid-based framework to generate different predictions. It can also be combined with the anchor-based MTP framework to avoid the expectation-maximization training process and visualize uncertainties at each time step for better optimization [Chai et al., 2020].

3.5 Other Techniques to Improve MTP

Improved Discriminators

Advanced discriminators in GAN models have been proposed to enhance the quality of generated trajectories. Parth and Alexandre [2019] and Huang et al. [2020] proposed improved discriminators to simplify adversarial training of recurrent neural networks. SC-GAN [Wang et al., 2020] enhances the discriminator to check scene compliance using distinguishable rasterized maps and scene images, while some methods propose improved discriminators to ensure social acceptability [Kothari and Alahi, 2022; van der Heiden et al., 2019].

Improved Sampling Techniques

Due to the limited number of samples, random sampling from MTP models may not cover all modes. Therefore, improved sampling techniques have been proposed to ensure coverage of the distribution. For example, Ma et al. [2021] proposed a post-processing method called Likelihood Diversity Sampling (LDS), which trains the sampling model by balancing the likelihood of individual trajectories and spatial separation between trajectories, thereby improving the quality and diversity of flow-based methods, and it can also be applied to other frameworks. Mangalam et al. [2021] proposed a test-time sampling technique that clusters sampled endpoints into K centers to cover predicted endpoints more broadly. Bae et al. [2022] proposed generating unbiased samples through a non-probabilistic sampling network based on Monte Carlo methods.

4 MTP Datasets and Benchmarks

Datasets and Benchmarks for Trajectory Prediction

Existing widely used benchmarks for MTP and DTP include ETH and UCY [Lerner et al., 2007], and the Stanford Drone Dataset [Robicquet et al., 2016] for pedestrians and NuScenes [Caesar et al., 2020], Argoverse [Chang et al., 2019], and Waymo [Ettinger et al., 2021] for vehicles. Each provides annotated trajectories and environmental information represented by videos, reference images, or high-definition (HD) maps.

Synthetic Datasets for Toy Experiments

The distribution of trajectories in each dataset is implicit, making it challenging to evaluate whether the model correctly conforms to the distribution. Therefore, simple and controllable synthetic datasets have been proposed for evaluation. For example, Amirian et al. [2019] proposed a toy dataset containing six groups of trajectories, each starting from a specific point and following three different paths to reach the endpoint. Chai et al. [2020] introduced a 3-way interaction toy dataset, with the probability of selecting left, middle, or right path sets. Experiments using these datasets highlight the mode collapse problem and social acceptability in current frameworks.

ForkingPath: A Special MITP Benchmark

Liang et al. [2020] pointed out that current trajectory prediction benchmarks have the same issue of providing only one possible ground truth trajectory for each agent, which is not suitable for MTP evaluation. To address this issue, they proposed the ForkingPath dataset, which provides multiple manually annotated ground truth trajectories for each agent to achieve visible ground truth distribution. Further research [Dendorfer et al., 2021; Ma et al., 2021] has also used it to compare predicted distributions with ground truth distributions.

5 Evaluation Metrics

In DTP, the default evaluation metrics are Average Displacement Error (ADE) and Final Displacement Error (FDE), which measure the l2 distance to the ground truth trajectory over all future time steps and the last future time step, respectively. Additionally, several metrics measuring social acceptability, such as collision rate, overlap rate, and off-road rate, are used to assess whether the predicted trajectory of agents collides with surrounding agents or enters inaccessible areas. The evaluation metrics for MTP need to consider all predictions, making them more challenging. In this section, we review these MTP metrics summarized in the classification in Figure 4 and their challenges.

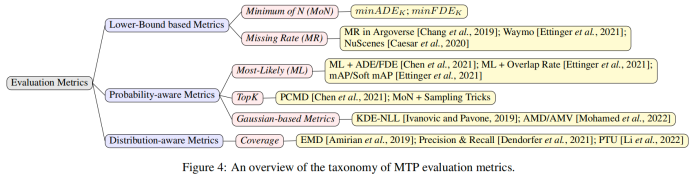
5.1 Lower Bound Based MTP Metrics

Lower bound-based MTP metrics are simple and widely used in MTP. Given K predicted trajectories, each prediction is compared with the ground truth, and the best score is recorded without considering the exact confidence. Thus, these metrics can be easily converted from DTP metrics and are valid for any models in trajectory prediction.

Minimum-of-N (MoN)

MoN was first proposed in [Gupta et al., 2018] and is the default metric for most MTP research. It calculates the minimum error among all predictions:

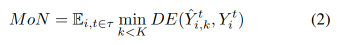
where DE can be any distance metric used in DTP. Many works adopt this strategy to make ADE and FDE applicable for multimodal predictions, abbreviated as and, which have become the default metrics in all multimodal trajectory prediction methods and benchmarks.

Miss Rate (MR)

Some vehicle trajectory prediction benchmarks like Waymo, Argoverse, and nuScenes use MR to indicate whether predictions can cover the ground truth. If the distance between the prediction and ground truth exceeds d meters according to their displacement error, the prediction misses the ground truth; otherwise, it hits. MR counts the scenes where all predictions miss the ground truth:

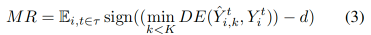
where FDE is used as the displacement metric in Argoverse and Waymo benchmarks, while ADE is used in NuScenes. The distance threshold d is 2 meters in Argoverse and NuScenes, while it is adjusted according to speed in Waymo benchmarks.

Challenge: Information Leakage

Lower bound-based metrics are sensitive to randomization and insufficient to represent model performance. Information leakage occurs during testing because only the best predictions will be used for evaluation based on the distance to the ground truth. This allows distributions with high entropy to achieve lower errors. For example, a Constant Velocity Model (CVM) [Schöoller et al., 2020] can even “outperform” deep learning-based models by adjusting angles to obtain a broader distribution. This further leads to unreliable indications of interactive processing. For example, predictions that violate social rules can be generated from DTP models without social interaction modules and ignored in MTP due to the selection of the best prediction.

Probability Known MTP Metrics

Probability known metrics measure how likely it is to draw basic facts from the predicted distribution. In contrast to lower bound metrics, MTP models need to mark the highest probability as the best prediction.

Most Likely (ML) Based Metrics

The simplest approach is to select the most probable prediction for DTP evaluation. For example, the ML metric [Chen et al., 2021] simply selects the most likely prediction for ADE and FDE calculations, as well as for overlap rate calculations in the Waymo benchmark. Similarly, Mean Average Precision (mAP) is used for Waymo benchmark testing [Ettinger et al., 2021]. If the most likely prediction matches the ground truth, it is considered a true positive; otherwise, it is a false positive. All other predictions are designated as false positives. It then calculates the area under the precision-recall curve. Starting from 2022, the Waymo benchmark uses Soft mAP, which is the same as mAP but ignores penalties for predictions other than the most likely prediction.

TopK Based Metrics

Chen et al. [2021] indicate that a single prediction cannot represent the entire distribution. Therefore, we can select candidates with probabilities greater than a threshold for MoN evaluation from M >> K predictions, called Probability Cumulative Minimum Distance (PCMD):

Then, the predictions with the top K probabilities are selected. However, if the probabilities for each prediction are not provided, this cannot be used. To address this issue, we can use sampling techniques from Section 3.5 to select K predictions.

Gaussian Based Metrics

If probabilities are not provided, another approach is to first estimate the Gaussian distribution by methods such as Kernel Density Estimation (KDE), which estimates the probability density function given a sequence of independent random variables, in the case of K discrete predictions. In trajectory prediction [Ivanovic and Pavone, 2019], KDE-NLL was first introduced as one of the evaluation metrics in MTP, calculating the average log-likelihood of the ground truth trajectory at each future time step:

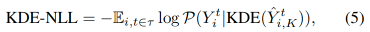
and further used in subsequent research, such as [Mangalam et al., 2020, 2021]. Mohamed et al. [2022] further improved KDE-NLL by proposing Average Mahalanobis Distance (AMD) and Average Maximum Eigenvalue (AMV), where AMD measures the distance between the ground truth and the generated distribution, and proposes Average Maximum Eigenvalue (AMV) to measure the confidence of predictions.

Challenge: Ground Truth May Not Be Most Likely

Probability known metrics assume that the ground truth is likely to be sampled with the highest probability. However, datasets are noisy, and predictions may be more reasonable than the ground truth based on observed cues, so they should not be penalized. For example, if an agent exhibits “zig-zag” behavior in pedestrian datasets and “sudden cut-in” behavior in vehicle datasets, how likely is this behavior to occur? In these cases, we believe that lower bound metrics are more appropriate.

5.3 Distribution Known Metrics

None of the above metrics penalize unacceptable predictions outside the ground truth distribution. The main obstacle is that only one ground truth is provided, and its distribution cannot be estimated. To address this issue, datasets like ForkingPath provide multiple ground truth trajectories for each agent so that we can directly assess the coverage of predicted distributions and ground truth distributions.

Coverage Based Metrics

Amirian et al. [2019] proposed the Earth Mover’s Distance (EMD) by using linear and distribution calculations between predicted samples and ground truth samples to calculate ADE results. Dendorfer et al. [2021] proposed recall and precision metrics for generative networks to measure coverage. Given sets of predicted and ground truth future trajectories, recall calculates how many predicted trajectories can find ground truth trajectories located within a specific range d.

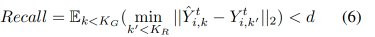
where KG is the number of predictions, and KR is the number of labeled ground truths for agent i. In other words, the predicted distribution should cover all ground truth trajectories. On the other hand, precision, also known as Trajectory Usage Percentage (PTU) in [Li et al., 2022], calculates the ratio of generated samples predicted outside the support of the ground truth distribution and penalizes distributions:

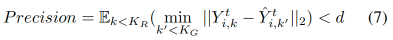
Challenge: Labor-Intensive

Clearly, distribution known metrics require human experts for additional annotation and correction of real-world datasets, which is labor-intensive. Moreover, even manual annotations cannot guarantee coverage of all modes. While synthetic datasets can alleviate this issue, they can only evaluate simple and unrealistic interactions. Therefore, most benchmarks do not use these metrics.

6 Conclusion and Future Directions

This paper provides a comprehensive overview of MTP through the classification of frameworks, datasets, and evaluation metrics, with an in-depth analysis and discussion of their advantages and issues. Finally, several future research directions are suggested as follows:

Better Evaluation Metrics

Evaluation metrics are crucial for guiding the design of model architectures and loss functions. Unfortunately, the current metrics described in Section 5 either ignore unacceptable predictions or are limited by datasets and frameworks. Therefore, it is necessary to propose more comprehensive evaluation metrics that can accurately represent the performance of MTP models without being constrained by datasets or frameworks.

Motion Planning Using Multimodal Predictions

We believe that MTP will ultimately be used for downstream tasks, such as motion planning and control in autonomous systems. Planning models can provide safe and collision-free routes based on trajectory predictions with multiple modalities. However, to our knowledge, motion planning and MTP are currently developed independently. To connect these two fields, we first suggest exploring MTP-aware motion planning models that can benefit from multimodal predictions. Then, the performance of these models can serve as evaluation metrics, and research can investigate MTP models with planning awareness to help motion planning models achieve better results.

Language-Guided Interpretable MTP

To build trustworthy and safe autonomous systems, interpretable MTP frameworks must be constructed to provide human-understandable decisions for multimodal predictions. Currently, most MTP frameworks provide multiple predictions without explaining their decisions [Kothari et al., 2021]. Although anchor-based MTP frameworks alleviate this issue by controlling the modality of each prediction using anchors, they are far from interpretable. Recently, Xue and Salim [2022] proposed a new prompt-based learning paradigm called PromptCast, indicating that human language can serve as a prompt to guide time series predictions in a question-and-answer format. Therefore, we suggest that language-guided MTP frameworks could be a reasonable solution for interpretable MTP. We believe that language can serve as a prompt to guide predictions of complex modalities and provide human-readable explanations for predicted future trajectories.

Lightweight MTP Frameworks

Predicting longer horizon trajectories is also beneficial, requiring larger K to cover all modalities. Additionally, some trajectory prediction models, such as YNet [Mangalam et al., 2021], use convolutional decoders to generate heatmaps and propose scene-compatible predictions. However, as shown in Figure 3, decoders in MTP frameworks are executed repeatedly, leading to excessive time and memory consumption. Therefore, exploring lightweight MTP frameworks could benefit real-time autonomous systems.

MTP with Out-of-Distribution (OOD) Modalities

Current MTP models’ predictions match existing modalities in the dataset, thus requiring the dataset to cover all types of modalities. Predicting OOD modalities is challenging, especially when datasets are biased and therefore not robust in unseen environments. Proposing a universal framework to tackle this issue would be interesting. Future directions could involve constructing more comprehensive datasets or considering methods for OOD problems in domain generalization to help address this issue.

Urban-Scale MTP

Current MTP focuses on future short-distance movements. However, we believe it can be extended to urban-scale location predictions: Human Mobility Prediction (HMP), which predicts the next Point of Interest (POI) based on previous locations and rich contextual information, such as the semantics of locations. HMP is inherently multimodal, as multiple POIs with different uncertainties can be accepted, thus the development of MTP can also be applied to it. Additionally, MobTCast [Xue et al., 2021] uses DTP to enhance the geographic context of HMP. Therefore, we believe that MTP can become a more powerful auxiliary task that considers the uncertainty of future POIs.

References

[1] Multimodal Trajectory Prediction: A Survey