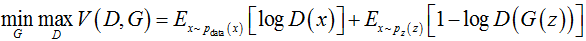Table of Contents
-
What is GAN?
-
What Can GAN Do?
-
Framework and Training of GAN
-
Similarities and Differences Between GAN and Other Generative Models
-
Existing Problems of GAN Models
(Continued from last issue)
3 Framework and Training of GAN
Previously, we mentioned that GAN consists mainly of two parts: the generator model and the discriminator model. Through the adversarial process, the generator’s ability to fit the distribution of real data can gradually improve. Now, we delve into the specific formalization and training process of GAN. Let G be the generator model, D be the discriminator model, z be the noise input to the generator, p(z) be the distribution of the input noise, and V(G,D) be the loss function of the GAN model. After training, the output of the generator is taken as the output of GAN.
|
Extension:The loss function of the GAN model is:
V(D,G) is a classic binary classification problem loss function, which defines the cross-entropy of binary classification. The training goal is to minimize the cross-entropy. Unlike general classification problems, all positive examples in the GAN model come from real samples, while all negative examples come from model samples. The GAN model can also be viewed as a zero-sum game problem between the discriminator and the generator, where the equilibrium point allows the generator to accurately reproduce the real data. |
The basic steps for training a GAN model are:
1) Obtain z~p(z) and input it into the generator model G;
2) Let the output of the generator x=G(z) be the corresponding model sample, and sample from real data to obtain the real sample x~pdata;
3) Mix model samples and real samples, and train the discriminator model D to maximize its ability to distinguish between the two types of samples, i.e.,
;
4) The generator model minimizes its error based on the training error from the discriminator model D, i.e.,
;
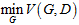5) Repeat the above steps until the discriminator model cannot distinguish between real samples and model samples, i.e., D*(x)=1/2. (Note: D* represents the ideal discriminator model)
Figure 6 shows the basic framework for training a GAN model.
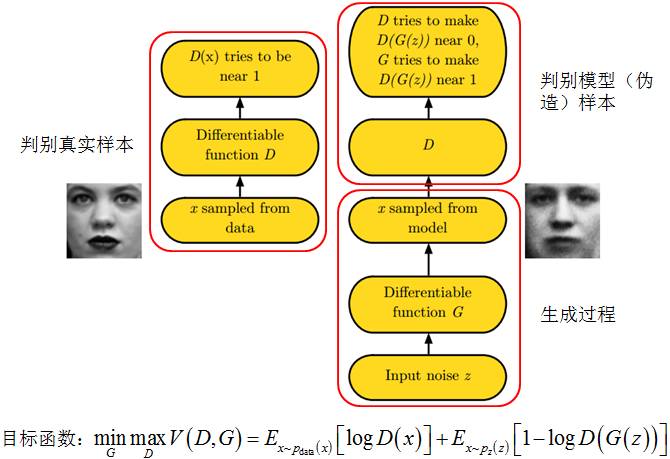
Figure 6 GAN Framework
Goodfellow et al. published a paper titled “Generative Adversarial Nets” in NIPS 2014, which vividly illustrates the training process of GAN. As shown in Figure 7, the black dotted line represents the distribution of real samples, the blue dashed line represents the accuracy of the discriminator model in identifying real samples from the given samples, and the green solid line represents the distribution fitted by the generator model. The bottom has two solid lines: z is set as the sampling space from a uniform distribution, while x is the mapping space transformed from z by the generator model G.
The initial state of the GAN model is shown in Figure 7 (a); after the training steps (1)~(3), we obtain the current optimal discriminator model D, which is used to distinguish between the current model samples and real samples (see Figure 7 (b)). Ideally,
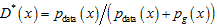Then, fixing the discriminator model D, we adjust the parameters of the generator model G so that the distribution of the generated samples approaches the distribution of real samples (see Figure 7 (c)); repeating the adjustment process of the discriminator model and the generator model, ultimately, under the convergence of the GAN model, the discriminator model D fails, and the distribution of generated samples is consistent with the distribution of real samples, concluding the training (see Figure 7 (d)).
Figure 7 Illustration of GAN Optimization Process
4 Similarities and Differences Between GAN and Other Generative Models
Next, we will compare GAN with models in the generative model family one by one, clarifying the advantages of GAN as a generative model.
Generative models primarily model the distribution of observed data, utilizing maximum likelihood to solve for the true sample distribution. Generally, we can divide this type of maximum likelihood solving methods into two categories: those with a specific probability density function form and those without a specific probability density function form. First, looking at those with a specific probability density function form, we can write their specific forms. Depending on their forms and the complexity of computation, they can be further divided into directly solvable and approximately computable categories. Directly solvable methods, such as Gaussian distribution, are common, as their computational forms are simple, allowing direct fitting of observations to solve for parameters in a specific distribution. Approximate computation is relatively more complicated; one common approach is to use mean field theory and variational approximations. Although Monte Carlo approximations are less guaranteed in convergence and less efficient, they are easier to implement and are thus often used for approximate estimation of probability density functions. However, methods given a specific probability density function form will always have model or prior/posterior constraints, which can easily lead to estimation errors due to inappropriate constraint information. In this regard, modeling methods without a specific probability density function form have advantages. These methods primarily approximate the true distribution through sampling and can be divided into two categories: one indirectly estimates the true sample distribution through sampling, such as the Generative Stochastic Networks proposed by Bengio et al. in 2014, which belongs to this category; the other directly estimates the true sample distribution through sampling, currently represented only by GAN. Compared to other generative models, GAN has the following advantages: 1) GAN is a direct estimate of the real sample distribution, eliminating the cumulative errors that arise from modeling the generation process using Markov chains; 2) GAN has no specific distribution form constraints; 3) By introducing adversarial modeling, GAN can gradually approximate the real sample distribution; 4) GAN can generate samples in parallel; 5) In practice, GAN has been shown to generate model samples that are subjectively perceived as superior.
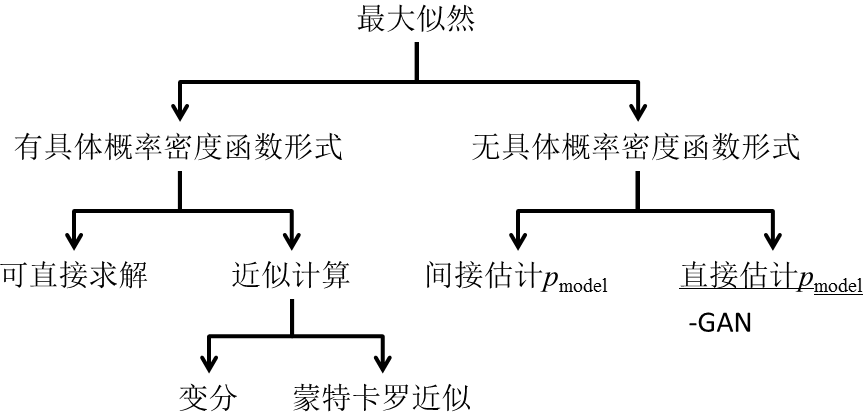
Figure 8 Classification Tree of Generative Models
5 Existing Problems of GAN Models
GAN models themselves also have a considerable number of issues, some of which still lack reasonable solutions, limiting their development in related fields. We will not elaborate too much on this part; related portions can be discussed in detail in future specific paper introductions. At the end of the article, I will list the relevant materials, and interested readers can refer to them. Here, we mainly discuss several problems encountered by GAN in image applications:
1) Difficult to Train.Due to the adversarial nature of the discriminator and generator models in GAN, if a fairly accurate discriminator model is obtained at the beginning of training that can distinguish a large number of generated model samples, the loss value for the generator will become very large, preventing proper updates of the model parameters. To solve this problem, it is necessary to modify the loss function of the model to better balance the discriminator and generator in GAN, allowing parameter updates under such circumstances. Currently, two common methods are: (i) using an approximate generator model loss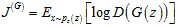
; (ii) adjusting the classification boundary of the discriminator model, labeling 1-α as real samples and 0+β as model samples. When α and β are greater than 0, the discriminator tends to force the generator to either produce real samples or continue generating similar model samples from the previous round (see Salimans et al. 2016).
2) Large Solution Space Leading to Suboptimal Convergence Results.Since GAN has no constraints, its large solution space makes it difficult to converge to a good fit for the real sample distribution. Currently, two common solutions are: 1) adding certain constraint conditions on the input z, such as the conditional constraint CGAN; 2) reducing the mapping space of the generator model, for example, learning only the residuals in LAGAN.
3) Model Collapse.GAN models often encounter situations where multiple inputs z correspond to the same model sample. Figure 9 illustrates a typical example of model collapse: for a target image of a two-dimensional ring lattice, GAN tends to converge to a single mode, resulting in an inability to reproduce the two-dimensional ring lattice image. In other image generation applications, the model collapse issue can also lead to insufficient diversity in the generated images. One possible solution is to change the order of optimization in the objective function, optimizing the generator model first and then the discriminator model, especially in the early stages of model optimization, which can help the generator produce more potential model samples with less constraint from the discriminator model. Another potential solution is to use minibatch features for training: this method divides real samples and model samples into small batches, with discrimination based on the feature conditions within each batch (see Salimans et al. 2016). Additionally, in unrolled GANs (Metz et al. 2016), it is suggested not to wait for the discriminator model to reach optimality before optimizing the generator model, but to optimize the generator model with a few iterative steps first, which can effectively avoid the model collapse issue.
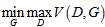
Figure 9 Typical Model Collapse Problem
4) GAN also faces issues in image generation results, such as inability to accurately count, perspective deviations in generated images, and global structure blurriness.As shown in Figure 10, generated animal images may have multiple heads, display multiple dimensions on a single plane, and exhibit structural issues such as misalignment of heads, hands, and feet. These problems currently limit the development of GAN, and corresponding solutions need to be proposed in future work.
Figure 10 Issues with Counting, Perspective, and Structure in GAN Generated Images
References
Bengio, Y., Thibodeau-Laufer, E., Alain, G., and Yosinski, J. Deep generative stochastic networks trainable by backprop. In ICML’2014.
Denton, E., Chintala, S., Szlam, A., and Fergus, R. Deep generative image models using a Laplacian pyramid of adversarial networks. In NIPS’15.
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., and Bengio, Y. (2014b). Generative adversarial networks. In NIPS’14.
Goodfellow, I. NIPS 2016 Tutorial: Generative Adversarial Networks. arXiv’16.
MirzaM, Osindero S. Conditional generative adversarial nets. arXiv’14.
Salimans, T., Goodfellow, I., Zaremba, W., Cheung, V., Radford, A., and Chen, X. Improved techniques for training gans. In NIPS’16.
Radford, A., Metz, L., and Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv’15.
GAN project: https://github.com/openai/improved-gan
iGAN project: https://github.com/junyanz/iGAN
DCGAN project: https://github.com/Newmu/dcgan_code
Summary
During discussions with colleagues, I found that using GAN can indeed enhance the generative capabilities of models, especially in generating sequential data. Originally, using maximum likelihood methods modeled by Markov chains had difficulty accurately depicting the entire sequence generation process, whereas GAN has this capability. The adversarial mechanism provided by the discriminator model can offer richer information to guide the optimization process of the originally unsupervised generative model. However, GAN still faces many issues, and it has not yet achieved good results in fields other than images. In practical applications, it tends to favor end-to-end learning, which may also be a limiting factor for GAN’s development in other areas.
Feel free to follow the author’s WeChat public account
