I am a master’s student at a double first-class university, and I am currently preparing for the 2024 autumn recruitment. While looking for internships in large model algorithm positions, I encountered many interesting interviews, so I decided to record these interview questions and share them with friends who, like me, are striving for a satisfactory offer!!!

Explaining the Basic Structure of Convolutional Neural Networks (CNN)

Interview Question

What is the basic structure of a Convolutional Neural Network (CNN)?

Answer

Question 1: What is a Convolutional Neural Network?

A Convolutional Neural Network (CNN) is a type of deep learning model that is particularly well-suited for processing data with a grid-like topology, such as images. CNNs effectively extract features from images and perform classification or regression through a combination of convolutional layers, pooling layers, and fully connected layers.

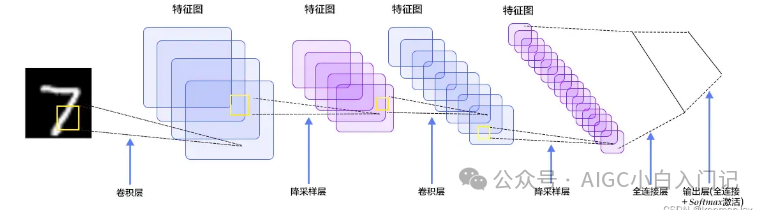
The entire process involves computations across the following layers:

• Input Layer: Input image and other information
• Convolutional Layer: Used to extract low-level features from images
• Pooling Layer: Prevents overfitting and reduces data dimensions
• Fully Connected Layer: Summarizes the low-level features and information obtained from the convolutional and pooling layers
• Output Layer: Produces the result with the highest probability based on the information from the fully connected layer

Question 2: Describe the Convolutional Layer?

Function: The convolutional layer is used to extract local features from the input data. By sliding a convolution kernel (filter) over the input data and calculating the dot product between the kernel and the input data, it generates a feature map.

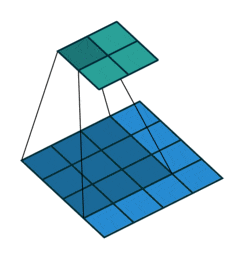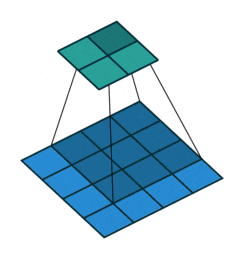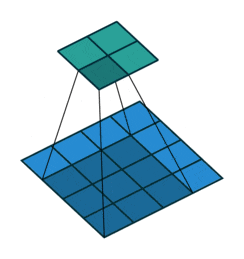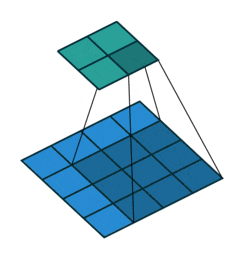
Key Parameters:

• Kernel Size (Kernel Size): The size of the convolution kernel, typically 3×3 or 5×5.
• Stride (Stride): The step size by which the convolution kernel moves, usually 1 or 2.
• Padding (Padding): Adding zeros to the edges of the input data to maintain the feature map size. Common padding methods include ‘valid’ (no padding) and ‘same’ (maintains feature map size).

Mathematical Formula:

Assuming the input data is , the convolution kernel is , and the bias is , the convolution operation can be represented as:

Where, represents the convolution operation, is the activation function (e.g., ReLU).

Question 3: Describe the Pooling Layer?

Function: The pooling layer is used for dimensionality reduction, reducing the size of the feature map while retaining important features. Common pooling operations include max pooling and average pooling.

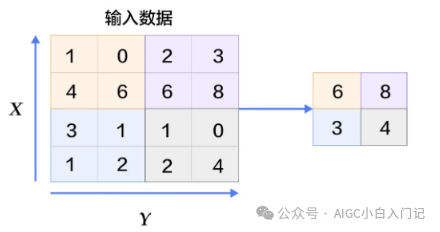
Key Parameters:

• Pooling Size (Pool Size): The size of the pooling kernel, typically 2×2.
• Stride (Stride): The step size by which the pooling kernel moves, usually the same as the pooling size.

Mathematical Formula: Assuming the input feature map is , the pooling size is , and the stride is 2, the max pooling operation can be represented as:

Question 4: Describe the Fully Connected Layer?

Function: The fully connected layer integrates the features extracted from the convolutional and pooling layers, outputting the final classification or regression results. Each neuron in the fully connected layer is connected to every neuron in the previous layer.

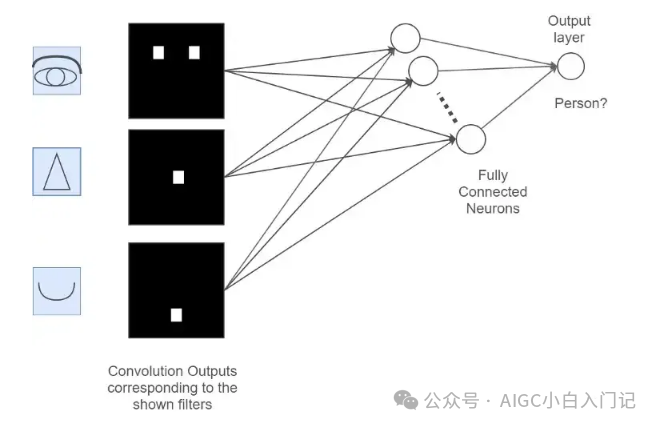
Mathematical Formula: Assuming the input feature vector is , the weight matrix is , and the bias vector is , the output of the fully connected layer can be represented as:

Where, is the activation function (e.g., ReLU or softmax).

Question 5: Describe the Activation Function?

Function: The activation function introduces non-linearity, allowing the neural network to learn complex functions. Common activation functions include ReLU, Sigmoid, and Tanh.

ReLU:

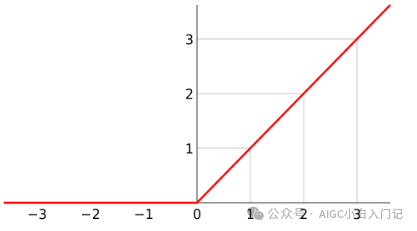
Sigmoid:

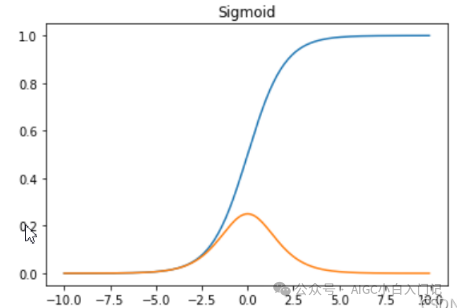
Tanh:

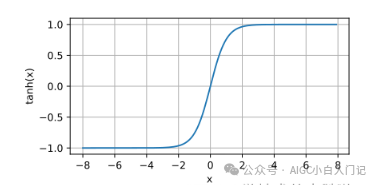
Question 6: Describe the Dropout Layer?

Function: The dropout layer is used to prevent overfitting. During training, a portion of the neurons’ outputs are randomly dropped, making the model more robust.

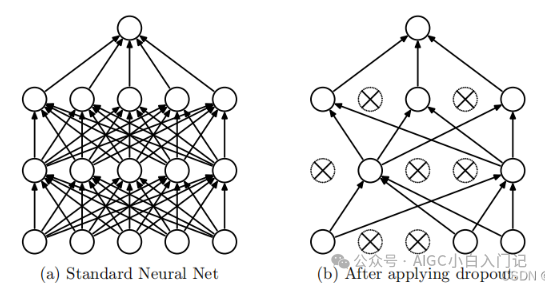
Key Parameters:

• Dropout Rate: The proportion of neurons to drop, typically between 0.2 and 0.5.

Question 7: Describe the Output Layer?

Function: The output layer generates the final prediction results. For classification tasks, the softmax activation function is typically used; for regression tasks, a linear activation function is usually employed.

Classification Task:

Regression Task:

An Example of a Typical CNN Structure

Assuming we have a CNN for image classification with an input image size of (224 x 224 x 3) (height, width, channels) and an output category count of 10. A typical CNN structure may be as follows:

1. Convolutional Layer 1:

• Kernel Size: 3×3
• Number of Kernels: 64
• Stride: 1
• Padding: same
• Activation Function: ReLU
• Output Size:

• Pooling Size: 2×2
• Stride: 2
• Output Size:

• Kernel Size: 3×3
• Number of Kernels: 128
• Stride: 1
• Padding: same
• Activation Function: ReLU
• Output Size:

• Pooling Size: 2×2
• Stride: 2
• Output Size:

• Kernel Size: 3×3
• Number of Kernels: 256
• Stride: 1
• Padding: same
• Activation Function: ReLU
• Output Size:

• Pooling Size: 2×2
• Stride: 2
• Output Size:

• Kernel Size: 3×3
• Number of Kernels: 512
• Stride: 1
• Padding: same
• Activation Function: ReLU
• Output Size:

• Pooling Size: 2×2
• Stride: 2
• Output Size:

• Input Size:
• Output Size: 4096
• Activation Function: ReLU
• Dropout Rate: 0.5

• Input Size: 4096
• Output Size: 4096
• Activation Function: ReLU
• Dropout Rate: 0.5

• Input Size: 4096
• Output Size: 10
• Activation Function: softmax

Code Example (Using PyTorch)

import torch
import torch.nn as nn
import torch.nn.functional as F

class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1)
        self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2)
        self.conv2 = nn.Conv2d(64, 128, kernel_size=3, stride=1, padding=1)
        self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
        self.conv3 = nn.Conv2d(128, 256, kernel_size=3, stride=1, padding=1)
        self.pool3 = nn.MaxPool2d(kernel_size=2, stride=2)
        self.conv4 = nn.Conv2d(256, 512, kernel_size=3, stride=1, padding=1)
        self.pool4 = nn.MaxPool2d(kernel_size=2, stride=2)
        self.fc1 = nn.Linear(14 * 14 * 512, 4096)
        self.fc2 = nn.Linear(4096, 4096)
        self.fc3 = nn.Linear(4096, 10)
        self.dropout = nn.Dropout(0.5)

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = self.pool1(x)
        x = F.relu(self.conv2(x))
        x = self.pool2(x)
        x = F.relu(self.conv3(x))
        x = self.pool3(x)
        x = F.relu(self.conv4(x))
        x = self.pool4(x)
        
        # Flatten the tensor for the fully connected layers
        x = x.view(-1, 14 * 14 * 512)
        
        x = F.relu(self.fc1(x))
        x = self.dropout(x)
        x = F.relu(self.fc2(x))
        x = self.dropout(x)
        x = self.fc3(x)
        
        return x

# Example usage
if __name__ == "__main__":
    # Create an instance of the CNN
    model = CNN()
    
    # Create a random input tensor of shape (batch_size, channels, height, width)
    # For example, a batch of 4 images of size 224x224 with 3 channels (RGB)
    input_tensor = torch.randn(4, 3, 224, 224)
    
    # Forward pass through the network
    output = model(input_tensor)
    
    # Print the output shape (batch_size, num_classes)
    print(output.shape)  # Should print: torch.Size([4, 10])

• Code Explanation

1. Define the CNN Class:

• <span>__init__</span> method defines the convolutional layers, pooling layers, fully connected layers, and dropout layer.
• <span>forward</span> method defines the forward propagation process, including convolution, activation, pooling, flattening, fully connected, and dropout operations.

• <span>nn.Conv2d</span> defines the convolutional layer, with parameters for input channels, output channels, kernel size, stride, and padding.
• <span>F.relu</span> applies the ReLU activation function.

• <span>nn.MaxPool2d</span> defines the max pooling layer, with parameters for pooling size and stride.

• <span>nn.Linear</span> defines the fully connected layer, with parameters for input features and output features.
• <span>F.relu</span> applies the ReLU activation function.
• <span>self.dropout</span> applies the dropout layer to prevent overfitting.

• <span>x.view(-1, 14 * 14 * 512)</span> flattens the multi-dimensional tensor output from the convolutional layers into a one-dimensional tensor for input into the fully connected layers.

• The output feature count of the last fully connected layer is 10, corresponding to 10 categories.
• The output layer does not apply an activation function, as it is typically applied in the loss function (e.g., cross-entropy loss) using the softmax activation function.

• Example Usage
• Create an instance of the CNN.
• Generate a random input tensor simulating a batch of 4 images of size 224×224 RGB images.
• Perform forward propagation through the network, where the output tensor shape should be <span>(4, 10)</span>, indicating the probabilities for 10 categories for 4 samples.

This example demonstrates how to define and use a simple CNN model using PyTorch. You can adjust the network structure and parameters according to specific tasks.