Essential Knowledge! 5 Major Deep Generative Models!

Essential Knowledge! 5 Major Deep Generative Models!

by
Essential Knowledge! 5 Major Deep Generative Models!
About 5200 words, recommended reading time 10 minutes.
This article summarizes commonly used deep learning models, providing an in-depth introduction to their principles and applications.
With the rise of models like Sora, diffusion, and GPT, deep generative models have once again become the focus of attention.
Deep generative models are a class of powerful machine learning tools that can learn the underlying distribution from input data and generate new sample data similar to the training data. They have been successfully applied in fields such as computer vision, density estimation, natural language processing, and speech recognition, providing a good paradigm for unsupervised learning.
This article summarizes commonly used deep learning models and provides an in-depth introduction to their principles and applications: VAE (Variational Autoencoder), GAN (Generative Adversarial Network), AR (Autoregressive Model such as Transformer), Flow (Flow Model), and Diffusion (Diffusion Model).

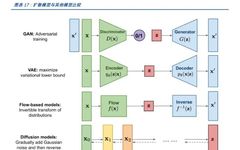
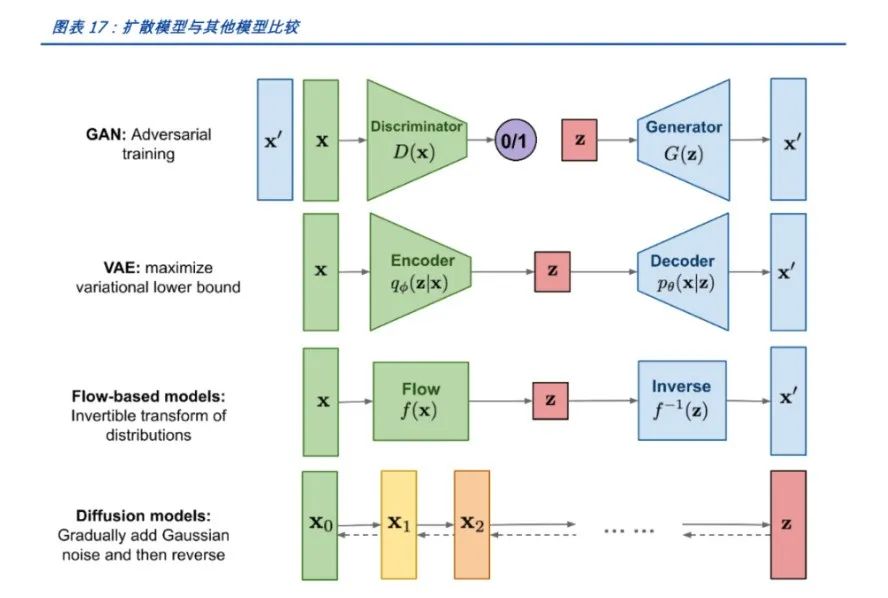
Essential Knowledge! 5 Major Deep Generative Models!

VAE (Variational Autoencoder)
Algorithm Principle:
VAE is a deep generative model proposed based on autoencoders, combining variational inference and Bayesian theory. The goal of VAE is to learn a model that can generate samples similar to the training data. It assumes that the latent variables follow a certain prior distribution (such as a standard normal distribution) and maps the input data to the posterior distribution of the latent variables through an encoder, then restores the latent variables into generated samples through a decoder. The training of VAE involves optimizing two parts: reconstruction error and KL divergence.

Essential Knowledge! 5 Major Deep Generative Models!

Training Process:
  1. Encoder: Encodes the input data x into the mean μ and standard deviation σ of the latent variable z.
  2. Sampling: Samples an ε from the standard normal distribution, calculates z = μ + ε * σ.
  3. Decoder: Decodes z into generated samples x’.
  4. Calculates reconstruction error (such as MSE) and KL divergence, optimizing model parameters to minimize their sum.
Advantages:
  • Can generate diverse samples.
  • The latent variables have a clear probabilistic interpretation.
Disadvantages:
  • The training process can be unstable.
  • The quality of generated samples may not be as good as other models.
Applicable Scenarios:
  • Data generation and interpolation.
  • Feature extraction and dimensionality reduction.
Python Example Code (implemented using PyTorch):
import torch
import torch.nn as nn
import torch.optim as optim
class VAE(nn.Module):
    def __init__(self, input_dim, hidden_dim):
        super(VAE, self).__init__()
        self.encoder = nn.Sequential(
            nn.Linear(input_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, 2 * hidden_dim)  # Mean and standard deviation
        )
        self.decoder = nn.Sequential(
            nn.Linear(hidden_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, input_dim),
            nn.Sigmoid()  # Binary data, use Sigmoid activation function
        )
    def reparameterize(self, mu, logvar):
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        return mu + eps * std
    def forward(self, x):
        h = self.encoder(x)
        mu, logvar = h.chunk(2, dim=-1)
        z = self.reparameterize(mu, logvar)
        x_recon = self.decoder(z)
        return x_recon, mu, logvar
# Example training process
model = VAE(input_dim=784, hidden_dim=400)
optimizer = optim.Adam(model.parameters(), lr=1e-3)
# Assume x is input data, batch_size is batch size
x = torch.randn(batch_size, 784)
recon_x, mu, logvar = model(x)
loss = nn.functional.binary_cross_entropy(recon_x, x, reduction='sum') + 0.5 * torch.sum(torch.exp(logvar) + mu.pow(2) - 1 - logvar)
optimizer.zero_grad()
loss.backward()
optimizer.step()
GAN (Generative Adversarial Network)
Algorithm Principle:
GAN consists of two parts: the generator and the discriminator. The generator’s task is to generate fake data as close to real data as possible, while the discriminator’s task is to distinguish whether the input data is real or generated by the generator. The two parts evolve together through competition and adversarial training, ultimately allowing the generator to produce samples very close to real data.

Essential Knowledge! 5 Major Deep Generative Models!

Training Process:
  1. The discriminator receives real data and fake data generated by the generator, training in a binary classification manner to optimize its ability to judge real or generated data.
  2. The generator attempts to generate more realistic fake data to deceive the discriminator based on the feedback from the discriminator.
  3. Alternately train the discriminator and generator until the discriminator can no longer distinguish between real and generated data or reaches a preset number of training rounds.
Advantages:
  • Can generate high-quality samples.
  • The training process is relatively free and not limited by data distribution.
Disadvantages:
  • Training can be unstable and easily fall into local optima.
  • Requires a large amount of computational resources.
Applicable Scenarios:
  • Image generation.
  • Text generation.
  • Speech recognition, etc.
Python Example Code (implemented using PyTorch):
import torch
import torch.nn as nn
import torch.optim as optim
# Discriminator
class Discriminator(nn.Module):
    def __init__(self, input_dim):
        super(Discriminator, self).__init__()
        self.fc = nn.Sequential(
            nn.Linear(input_dim, 128),
            nn.LeakyReLU(0.2),
            nn.Linear(128, 1),
            nn.Sigmoid()
        )
    def forward(self, x):
        return self.fc(x)
# Generator
class Generator(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(Generator, self).__init__()
        self.fc = nn.Sequential(
            nn.Linear(input_dim, 128),
            nn.ReLU(),
            nn.Linear(128, output_dim),
            nn.Tanh()
        )
    def forward(self, x):
        return self.fc(x)
# Example training process
discriminator = Discriminator(input_dim=784)
generator = Generator(input_dim=100, output_dim=784)
optimizer_D = optim.Adam(discriminator.parameters(), lr=0.0002)
optimizer_G = optim.Adam(generator.parameters(), lr=0.0002)
criterion = nn.BCEWithLogitsLoss()
# Assume real_data is real data, batch_size is batch size
real_data = torch.randn(batch_size, 784)
# Train the discriminator
for p in discriminator.parameters():
    p.requires_grad = True
for p in generator.parameters():
    p.requires_grad = False
noise = torch.randn(batch_size, 100)
fake_data = generator(noise)
real_loss = criterion(discriminator(real_data), torch.ones_like(real_data))
fake_loss = criterion(discriminator(fake_data.detach()), torch.zeros_like(real_data))
discriminator_loss = real_loss + fake_loss
optimizer_D.zero_grad()
discriminator_loss.backward()
optimizer_D.step()
# Train the generator
for p in discriminator.parameters():
    p.requires_grad = False
for p in generator.parameters():
    p.requires_grad = True
noise = torch.randn(batch_size, 100)
fake_data = generator(noise)
gen_loss = criterion(discriminator(fake_data), torch.ones_like(real_data))
optimizer_G.zero_grad()
gen_loss.backward()
optimizer_G.step()

AR (Autoregressive Model)

Algorithm Principle: The autoregressive model is a generative model based on sequential data, generating data by predicting the value of the next element in the sequence. Given a sequence (x_1, x_2, …, x_n), the autoregressive model attempts to learn the conditional probability distribution (P(x_t | x_{t-1}, …, x_1)), where (t) indicates the current position in the sequence. The AR model can be implemented using structures such as recurrent neural networks (RNN) or Transformers, analyzed here as an example of the Transformer.
In the early stages of deep learning, convolutional neural networks (CNNs) achieved significant success in image recognition and natural language processing. However, as task complexity increased, sequence-to-sequence (Seq2Seq) models and recurrent neural networks (RNNs) became common methods for processing sequential data. Although RNNs and their variants perform well on certain tasks, they often encounter gradient vanishing and model degradation issues when handling long sequences. To address these issues, the Transformer model was proposed, and subsequent large models like GPT and BERT have achieved excellent performance based on Transformers!

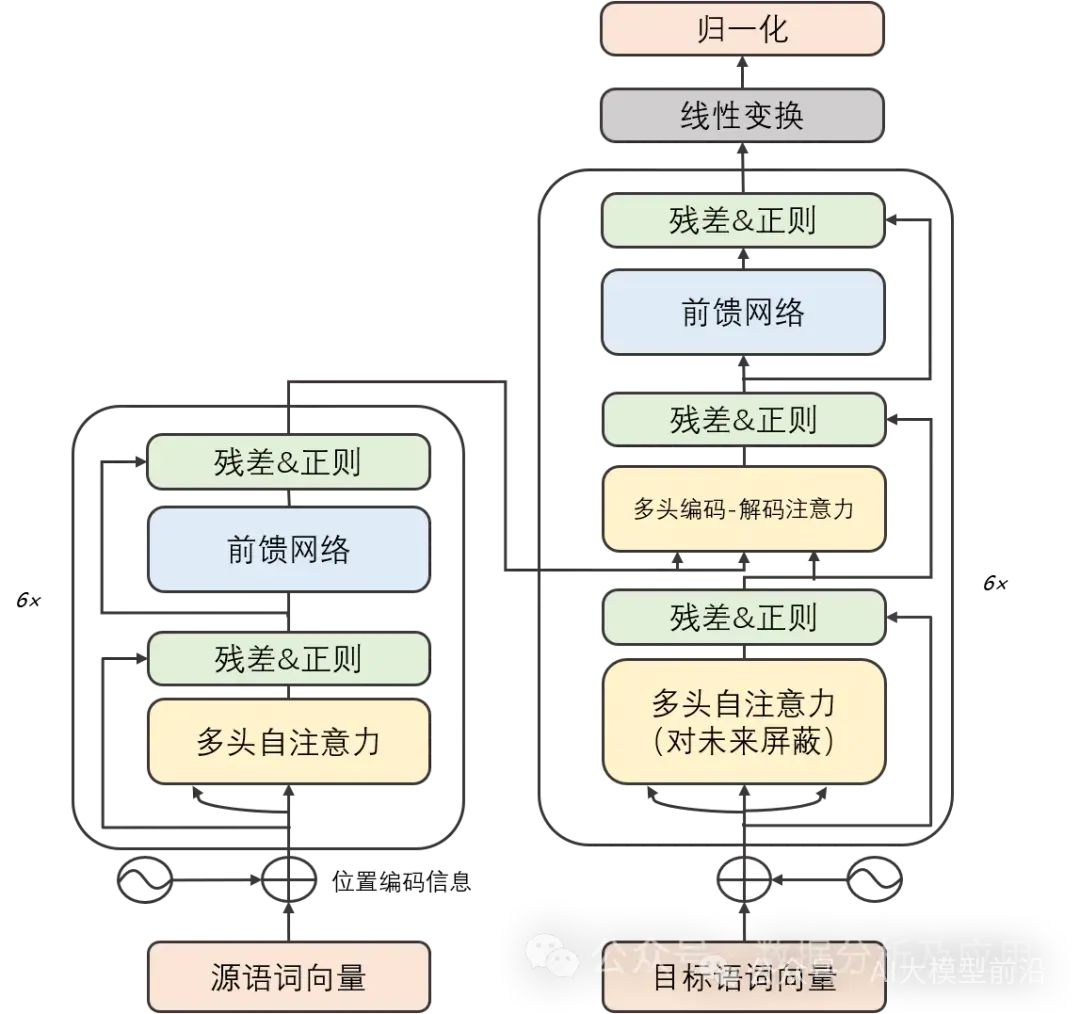
Essential Knowledge! 5 Major Deep Generative Models!

Model Principle:

The Transformer model cleverly combines the encoder and decoder components, each consisting of several identical layers stacked together. These layers ingeniously combine self-attention sublayers with linear feedforward neural network sublayers. The self-attention sublayer skillfully utilizes the dot-product attention mechanism to weave unique representations for each position in the input sequence, while the linear feedforward neural network sublayer draws on the insights from the self-attention layer to produce informative output representations. Notably, both the encoder and decoder are equipped with a positional encoding layer specifically designed to capture the positional context in the input sequence.
Model Training:
The training of the Transformer model relies on backpropagation and optimization algorithms, such as stochastic gradient descent. During training, it meticulously calculates the gradient of the loss function with respect to the weights and uses optimization algorithms to fine-tune these weights to minimize the loss function. To accelerate training and enhance the model’s generalization capability, practitioners often employ regularization techniques and ensemble learning strategies.
Advantages:
  1. Gradient vanishing and model degradation problems are resolved: The Transformer model, with its unique self-attention mechanism, can effectively capture long-term dependencies in sequences, freeing it from the shackles of gradient vanishing and model degradation.
  2. Outstanding parallel computing capability: The computational architecture of the Transformer model has inherent parallelism, allowing for rapid training and inference on GPUs.
  3. Excellent performance across multiple tasks: With its strong feature learning and representation capabilities, the Transformer model exhibits outstanding performance in various tasks, including machine translation, text classification, and speech recognition.
Disadvantages:
  1. High computational resource demand: Due to the parallelism of the Transformer model, both training and inference processes require substantial computational resource support.
  2. Sensitive to initialization weights: The Transformer model is highly selective about the choice of initialization weights; improper initialization can lead to training instability or overfitting issues.
  3. Limited handling of long-term dependencies: Although the Transformer model effectively addresses gradient vanishing and model degradation issues, it still faces challenges when processing extremely long sequences.
Application Scenarios:
The Transformer model has a wide range of applications in natural language processing, covering machine translation, text classification, text generation, and more. Additionally, the Transformer model shines in image recognition, speech recognition, and other fields.
Python Example Code:
import torch
import torch.nn as nn
import torch.optim as optim
# This example is only for illustrating the basic structure and principles of the Transformer. Actual Transformer models (like GPT or BERT) are much more complex and require more preprocessing steps such as tokenization, padding, masking, etc.
class Transformer(nn.Module):
    def __init__(self, d_model, nhead, num_encoder_layers, num_decoder_layers, dim_feedforward=2048):
        super(Transformer, self).__init__()
        self.model_type = 'Transformer'
        # encoder layers
        self.src_mask = None
        self.pos_encoder = PositionalEncoding(d_model, max_len=5000)
        encoder_layers = nn.TransformerEncoderLayer(d_model, nhead, dim_feedforward)
        self.transformer_encoder = nn.TransformerEncoder(encoder_layers, num_encoder_layers)
        # decoder layers
        decoder_layers = nn.TransformerDecoderLayer(d_model, nhead, dim_feedforward)
        self.transformer_decoder = nn.TransformerDecoder(decoder_layers, num_decoder_layers)
        # decoder
        self.decoder = nn.Linear(d_model, d_model)
        self.init_weights()
    def init_weights(self):
        initrange = 0.1
        self.decoder.weight.data.uniform_(-initrange, initrange)
    def forward(self, src, tgt, teacher_forcing_ratio=0.5):
        batch_size = tgt.size(0)
        tgt_len = tgt.size(1)
        tgt_vocab_size = self.decoder.out_features
        # forward pass through encoder
        src = self.pos_encoder(src)
        output = self.transformer_encoder(src)
        # prepare decoder input with teacher forcing
        target_input = tgt[:, :-1].contiguous()
        target_input = target_input.view(batch_size * tgt_len, -1)
        target_input = torch.autograd.Variable(target_input)
        # forward pass through decoder
        output2 = self.transformer_decoder(target_input, output)
        output2 = output2.view(batch_size, tgt_len, -1)
        # generate predictions
        prediction = self.decoder(output2)
        prediction = prediction.view(batch_size * tgt_len, tgt_vocab_size)
        return prediction[:, -1], prediction
class PositionalEncoding(nn.Module):
    def __init__(self, d_model, max_len=5000):
        super(PositionalEncoding, self).__init__()
        # Compute the positional encodings once in log space.
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len).unsqueeze(1).float()
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * -(torch.log(torch.tensor(10000.0)) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)
        self.register_buffer('pe', pe)
    def forward(self, x):
        x = x + self.pe[:, :x.size(1)]
        return x
# Hyperparameters
d_model = 512
nhead = 8
num_encoder_layers = 6
num_decoder_layers = 6
dim_feedforward = 2048
# Instantiate model
model = Transformer(d_model, nhead, num_encoder_layers, num_decoder_layers, dim_feedforward)
# Randomly generated data
src = torch.randn(10, 32, 512)
tgt = torch.randn(10, 32, 512)
# Forward pass
prediction, predictions = model(src, tgt)
print(prediction)
Flow (Flow Model)
Algorithm Principle: Flow models are a type of deep generative model based on invertible transformations. They transform simple distributions (such as uniform or normal distributions) into complex data distributions through a series of invertible transformations.

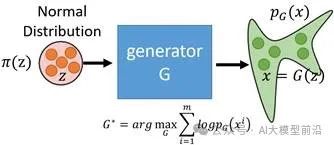
Essential Knowledge! 5 Major Deep Generative Models!

Training Process: In the training phase, the flow model learns the parameters of the invertible transformations by minimizing the loss function between samples in the latent space and the real data.
Advantages:
  • Can efficiently perform sample generation and density estimation.
  • Has invertibility, facilitating backpropagation and optimization.
Disadvantages:
  • Designing suitable invertible transformations can be challenging.
  • For high-dimensional data, flow models may struggle to capture complex dependencies.
Applicable Scenarios: Flow models are suitable for tasks such as image generation, audio generation, and density estimation.
Python Example Code:
import torch
import torch.nn as nn
class FlowModel(nn.Module):
    def __init__(self, input_dim, hidden_dim):
        super(FlowModel, self).__init__()
        self.transform1 = nn.Sequential(
            nn.Linear(input_dim, hidden_dim),
            nn.Tanh()
        )
        self.transform2 = nn.Sequential(
            nn.Linear(hidden_dim, input_dim),
            nn.Sigmoid()
        )
    def forward(self, x):
        z = self.transform1(x)
        x_hat = self.transform2(z)
        return x_hat, z
Diffusion Model
The Diffusion Model is a type of deep generative model inspired by the diffusion process in physics. Unlike traditional generative models (like VAE, GAN), the Diffusion Model generates data by simulating the gradual diffusion of data from random noise to target data. This model has shown outstanding performance in image generation, text generation, and audio generation.

Essential Knowledge! 5 Major Deep Generative Models!

Algorithm Principle:
The basic idea of the Diffusion Model is to view the data generation process as a Markov chain. Starting from the target data, at each step, it approaches random noise until reaching a pure noise state. Then, through a reverse process, it gradually recovers to the target data from pure noise. This process is typically described by a series of conditional probability distributions.
Training Process:
  1. Forward Process: Starting from real data, gradually add noise until reaching a pure noise state. During this process, the noise level at each step needs to be calculated and saved.
  2. Reverse Process: Starting from pure noise, gradually remove noise until recovering to the target data. In this process, a neural network (usually a U-Net structure) is used to predict the noise level at each step and generate data accordingly.
  3. Optimization: Train the model by minimizing the difference between real data and generated data. Common loss functions include MSE (Mean Squared Error) and BCE (Binary Cross Entropy).
Advantages:
  1. High generation quality: The Diffusion Model can generate high-quality data due to its stepwise diffusion and recovery process.
  2. Strong interpretability: The generation process of the Diffusion Model has clear physical meaning, making it easier to understand and explain.
  3. Good flexibility: The Diffusion Model can handle various types of data, including images, text, and audio.
Disadvantages:
  1. Long training time: The Diffusion Model requires a lengthy training time due to the multiple steps of diffusion and recovery.
  2. High computational resource demand: To ensure generation quality, the Diffusion Model typically requires substantial computational resources, including memory and computational power.
Applicable Scenarios:
The Diffusion Model is suitable for scenarios requiring high-quality data generation, such as image generation, text generation, and audio generation. Additionally, due to its strong interpretability and good flexibility, the Diffusion Model can also be applied to other fields requiring deep generative models.
Python Example Code:
import torch
import torch.nn as nn
import torch.optim as optim
# Define U-Net model
class UNet(nn.Module):
    # ... omitted model definition...
# Define Diffusion Model
class DiffusionModel(nn.Module):
    def __init__(self, unet):
        super(DiffusionModel, self).__init__()
        self.unet = unet
    def forward(self, x_t, t):
        # x_t is the data at the current moment, t is the noise level
        # Use U-Net to predict noise level
        noise_pred = self.unet(x_t, t)
        # Generate data based on noise level
        x_t_minus_1 = x_t - noise_pred * torch.sqrt(1 - torch.exp(-2 * t))
        return x_t_minus_1
# Initialize model and optimizer
unet = UNet()
model = DiffusionModel(unet)
optimizer = optim.Adam(model.parameters(), lr=0.001)
# Training process
for epoch in range(num_epochs):
    for x_real in dataloader:  # Get real data from data loader
        # Forward process
        x_t = x_real  # Start from real data
        for t in torch.linspace(0, 1, num_steps):
            # Add noise
            noise = torch.randn_like(x_t) * torch.sqrt(1 - torch.exp(-2 * t))
            x_t = x_t + noise * torch.sqrt(torch.exp(-2 * t))
            # Calculate predicted noise
            noise_pred = model(x_t, t)
            # Calculate loss
            loss = nn.MSELoss()(noise_pred, noise)
            # Backpropagation and optimization
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
By analyzing and comparing these five common generative models: GAN, VAE, Flow, Diffusion, and AR, we can see the advantages and disadvantages of different models and their applicable scenarios. VAE and GAN are two commonly used deep generative models that generate samples based on Bayesian probability theory and adversarial training, respectively. The AR model is suitable for handling data with temporal dependencies, such as sequential data. Flow models and Diffusion models exhibit good stability and diversity in sample generation but require high computational costs. Future research on generative models may further explore the stability and trainability of models, as well as how to improve the quality and diversity of generated samples.
Editor: Wang Jing

About Us

Data Party THU, as a data science public account backed by the Tsinghua University Big Data Research Center, shares cutting-edge data science and big data technology innovation research dynamics, continuously disseminates data science knowledge, and strives to build a platform for gathering data talents, creating the strongest group of big data in China.

Essential Knowledge! 5 Major Deep Generative Models!

Sina Weibo: @Data Party THU

WeChat Video Account: Data Party THU

Today’s Headlines: Data Party THU

Leave a Comment