
On March 26, 2024, Professor Huang Jiajun’s team from City University of Hong Kong, in collaboration with Tencent AI Lab and Shanghai Ruige Pharmaceutical, published an article in Nature Communications titled “A Dual Diffusion Model Enables 3D Molecule Generation and Lead Optimization Based on Target Pockets.”

The authors proposed a Pocket-based Molecular Diffusion Model (PMDM) for generating three-dimensional molecules targeting specific targets. PMDM consists of a dual diffusion model, which possesses both local and global conditional equivariant diffusion, allowing it to fully consider the protein information characterized by conditional probability for effective molecule generation. Experimental results demonstrate that the model’s performance surpasses existing methods.
Background
Structure-based generative chemical models are crucial in computer-aided drug discovery, as they explore vast chemical spaces to design ligands with high binding affinity to targets. However, existing generative models face bottlenecks due to the limitations of autoregressive sampling, and their computational efficiency still needs improvement.
Method
Figure 1 outlines the conditional generative model PMDM, clarifying its structural components and the processes involved in training and sampling. PMDM gradually introduces Gaussian noise during the forward process while employing a parameterized backward process to iteratively eliminate noise (Figure 1a). The model consists of two equivariant graph neural networks that obtain molecular embeddings and target pocket embeddings, respectively (Figure 1b). To facilitate conditional generation, the authors designed a contextual mechanism to combine the semantic and geometric information of protein pockets, using cross-attention layers to compute attention scores between molecules and protein pockets.
Additionally, PMDM employs a dual diffusion strategy that enables the model to recognize the interaction forces between different atoms within a molecule. This strategy includes constructing two types of virtual edges. Firstly, atom pairs with distances below the local threshold τl are bonded through covalent local edges, as chemical bonds tend to dominate interactions when atoms are close. Secondly, PMDM establishes global edges connecting to the remaining atom pairs to simulate van der Waals forces for atoms with distances greater than the local threshold τl but less than the global threshold τg (Figure 1d). Furthermore, the authors designed an equivariant dynamic kernel that accommodates transformations such as translation, rotation, reflection, and arrangement consistent with molecular geometry. To ensure the generated molecules fit structural pockets, the pocket positions are kept fixed during the hidden state update process of the dual equivariant encoder.
During the training phase, both the molecules and their corresponding binding protein pockets are treated as three-dimensional point clouds. In the forward process of PMDM, the input molecules undergo diffusion, akin to phenomena observed in nonequilibrium thermodynamics, with the sampling time steps derived from the joint distribution. Meanwhile, the protein pocket input is maintained as fixed conditional information (Figure 1c). The primary goal of PMDM is to learn how to reverse this process, thereby modeling the conditional data distribution. This allows for the efficient generation of precise molecules with high binding affinity when pocket information is fixed. At each time step, the model outputs a score that represents the log density of the data points. The evidence lower bound (ELBO) objective is derived from these scores and serves as the loss function.
In the sampling phase, the data state is initialized through probabilistic sampling. Given the target pocket protein, the transition probabilities are obtained through PMDM’s dual equivariant encoder. The final molecules are generated through progressive sampling. Ultimately, the argmax function is used to identify the atomic types of the molecules, which directly selects the atomic type with the highest value as output by the model.
Figure 1 Structure of PMDM
The diffusion model is represented as two Markov chains: the diffusion process and the reverse process (i.e., the denoising process). The diffusion process iteratively adds Gaussian noise to the data based on a variance-preserving schedule, while the reverse process progressively refines the data until the noise is eliminated, restoring the true data. The improvement goal of the diffusion model is to learn the reverse process through parameterized neural networks.
The diffusion process gradually spreads the actual data distribution into a predefined noise distribution over T time steps. The transformations at each time step are set as Gaussian distributions. The entire process is represented as a fixed Markov chain that gradually adds Gaussian noise to the data according to a variance schedule. It can be observed that if the time steps are sufficiently large, the final distribution will be closer to a standard Gaussian distribution.
To recover the true data from the diffusion data obtained during the diffusion process, a reverse process needs to be designed. This process is also a learnable parameter Markov chain that maximizes the probability of the training data. Since directly calculating the likelihood function is tricky, the diffusion model employs the evidence lower bound (ELBO) for optimization. In fact, the ultimate goal of the reverse process is to learn the noise added during the diffusion process.
Unlike pure diffusion models, PMDM is a conditional diffusion model, guided by pocket proteins as conditional probabilities for molecule generation. Thus, it is necessary to establish a model that obtains the ligand distribution binding to pocket proteins. By utilizing cross-attention layers, the conditional semantic information of pocket proteins can be effectively fused with various modalities. Specifically, PMDM designs a dual equivariant diffusion model to learn and generate the geometric shapes of binding molecules, simulating localized chemical bond graphs and global distance graphs. To ensure the relative distances between ligands and proteins, an equivariant graph neural network (EGNN) is employed to process the entire pocket, using the pocket’s geometric shape as conditional information.
As shown in Figure 1b, the equivariant graph neural network SchNet is first used to encode the semantic information of the protein. SchNet is a graph neural network that simulates molecular quantum interactions in three-dimensional space. It consists of continuous filter convolution layers designed to model atomic systems while maintaining invariance, achieving advanced performance for balancing molecular and molecular dynamics trajectories. Similarly, PMDM uses another SchNet to project the ligand atomic features into an intermediate representation, fusing the semantic information of the protein and the hidden information of the ligand through a cross-attention mechanism, transforming the attention matrix into a standard normal distribution. Specifically, the protein information is used as a query to calculate attention scores. The output of the cross-attention layer uses the protein semantic information as conditional context.
The geometric shape of the molecules is invariant to rotation and translation, a property that should be considered when designing the diffusion model Markov kernel. In fact, the desired property can be achieved using equivariant Markov kernels. Since the geometric shapes of molecules in three-dimensional generation can be represented as point clouds, edges must be manually constructed for the point clouds to input them into the subsequent equivariant Markov kernel. Specifically, edges with lengths less than the radius τl are defined as local edges to simulate covalent bonds, while edges with lengths between τl and τg are defined as global edges to capture information about van der Waals forces and other long-range interactions, as shown in Figure 1d. The authors set the local radius τl to 3 Å, which can encompass almost all chemical bonds, while the global radius τg is set to 6 Å. The one-hot encoded atomic features and coordinates with local and global edges are input into the dual equivariant encoder. In summary, the local equivariant encoder simulates the forces within the molecule through local edges, akin to real chemical bonds, while the global equivariant encoder captures interaction information between distant atoms through global edges, such as van der Waals forces.
In addition to the semantic information of the conditional protein, the spatial information of the conditional protein must also be considered to ensure that the generated ligands can fit the pocket structure without collision issues. Here, both the ligand and protein are combined as a complete pocket input for the equivariant kernel. Therefore, a similar approach is needed to construct local and global edges for the input pocket. PMDM models the shape of the pocket by constructing such edges and ensures that the ligand can independently aggregate neighborhood information through the message-passing process of the graph neural network. Since the pocket spatial information is used as a condition, the position of the protein is kept fixed during the update process of each layer of the equivariant kernel.
As illustrated in Figure 1c, PMDM samples from the uniform distribution of each iteration during training. From another perspective, it integrates multiple small models to learn the reverse process. Unlike the sampling strategy that starts from scratch with standard Gaussian distributed molecular noise, the given fragment information should be fixed as the starting point for iterations. Here, a masking strategy is employed to simulate the sampling process from scratch. During each iteration, the molecular fragments are masked according to the corresponding time steps, and the identification of atomic types and coordinates is the same as in the sampling process from scratch. Finally, the fragment data is combined with the denoised part to obtain the complete molecule.
Results
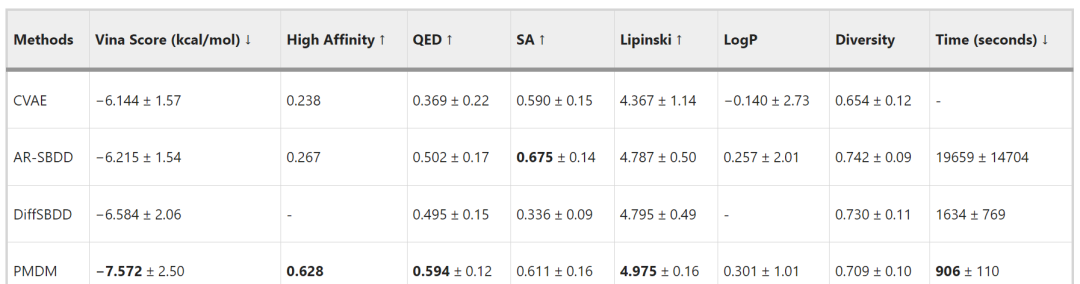
The authors compared PMDM with several representative methods. As shown in Table 1, the comparison was made using the following metrics: (1) The Vina score estimates the binding affinity between the ligand and the target pocket, which is the most important measure of how well the generated molecule fits a specific protein pocket, with lower values being better; (2) High affinity refers to the percentage of cases in the test set where the Vina score is higher than that of baseline molecules, with higher percentages being better; (3) QED estimates the drug-likeness of the molecule by combining several ideal molecular properties, with higher values being better; (4) SA (synthetic accessibility) indicates the synthetic accessibility of the molecule, with higher values being better; (5) The Lipinski coefficient measures how many of the 5 Lipinski rules a drug adheres to, with higher values being better; (6) LogP indicates the octanol-water partition coefficient; if the molecule is a good drug candidate, this coefficient should be between -0.4 and 5.6. Since in most cases, LogP does not exceed 1, higher values are generally considered better; (7) Diversity indicates the dissimilarity of molecules generated for each pocket, with higher values being better; (8) Time is the average time taken to generate 100 samples for each pocket, with shorter times being better. PMDM surpassed existing methods in 6 out of 8 metrics.
Table 1 Comparison with Other Methods
The authors designed ablation experiments to compare the model’s performance when removing cross-attention or local information. Although the training time was shortened for the ablation models, the performance on key metrics such as Vina scores, affinity, and Lipinski scores generally decreased. The results highlight the importance of cross-attention and local information for PMDM.
Table 2 Ablation Experiment
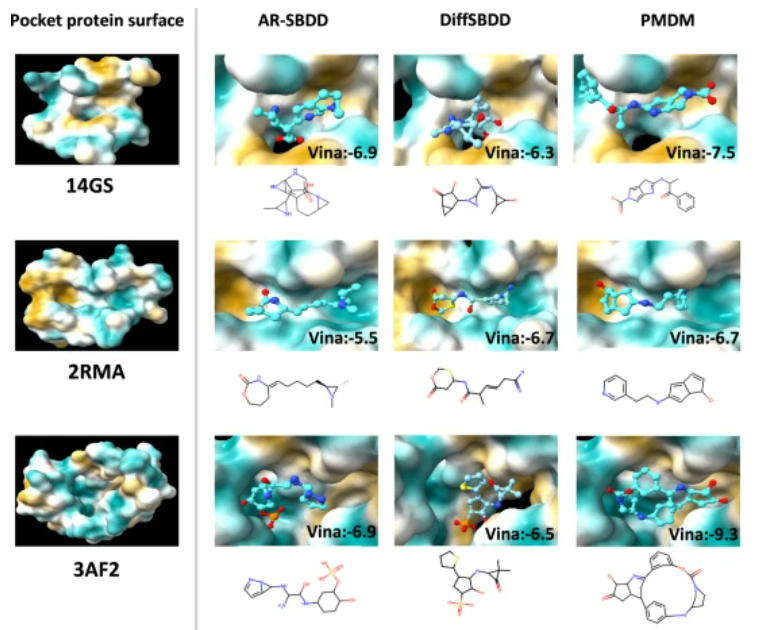
The authors also conducted case analyses, selecting three pocket proteins for visualization as representative samples. As shown in Figure 2, for the three targeted pocket proteins 14GS, 2RMA, and 3AF2, AR-SBDD and DiffSBDD tend to produce unstable three-atom rings, while the proposed model PMDM avoids the generation of such unstable rings. Although the dataset contains only 3% of three-atom rings, the AR-SBDD method produces more of these unstable structures, indicating that these methods get trapped in local optima and fail to learn the data distribution well. In contrast, PMDM considers the shape of the pocket holes and generates larger, more complex rings with lower Vina scores and better performance.
Conclusion
Source | Zhiyuan Bang

