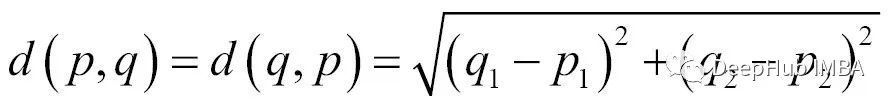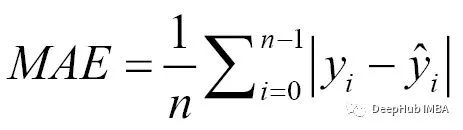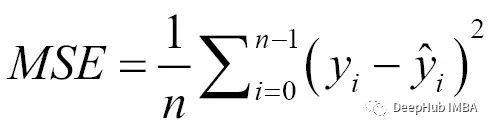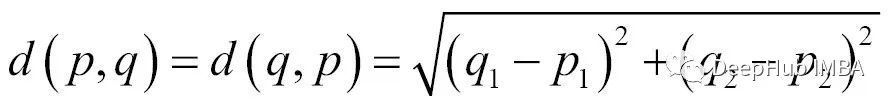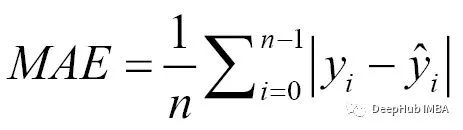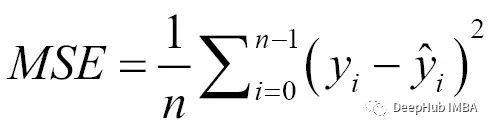Skip to content

This article is about 1700 words, and it is recommended to read for 7minutes.
This article compares KNN with simple linear regression.
Generally, k-Nearest Neighbor (KNN) is used to solve classification problems; in fact, KNN is a simple algorithm that can be applied to both data classification and prediction. In this article, we will compare it with simple linear regression.
The KNN model is a simple model that can be used for both regression and classification tasks. Most machine learning algorithms are described using its name, and KNN is no exception, using a space to represent the metric of neighbors, where the metric space defines the distance between them based on the features of the set members. For each test instance, the neighborhood is used to estimate the value of the response variable. The estimation can be done using up to k neighbors, where hyperparameters control the learning method of the algorithm; these are not estimated based on training data but are selected based on some distance function for the nearest k neighbors.
In this article, we will focus on binary classification; to avoid ties, k is usually set to an odd number. Unlike classification tasks, in regression tasks, the feature vector is associated with real-valued scalars rather than labels, and KNN predicts by averaging or weighted averaging the response variable.
Lazy Learning and Non-Parametric Models
Lazy learning is a hallmark of KNN. Lazy learners, also known as instance-based learners, rarely or never process the training data. Unlike active learning algorithms such as linear regression, KNN does not estimate the parameters of a model that generalizes the training data during the training phase. Lazy learning has its pros and cons; the cost of training an active learner can be high, but the cost of making predictions using the generated model is low. Simple results can be predicted by multiplying coefficients by features and adding bias parameters, which has low computational costs and fast prediction speeds. However, the cost for a lazy learner to make predictions is high because KNN predictions require calculating the distances between test instances and training instances, meaning all training data must be accessed.
Parametric models use a fixed number of parameters or coefficients to summarize the data. Regardless of how many training instances are used, the number of parameters remains constant. Non-parametric might seem like a misnomer because it does not mean that the model has no parameters; rather, it means that the number of parameters varies with the amount of training data.
Non-parametric models can be useful when the relationship between the response variable and explanatory variables is not well understood. KNN is such a non-parametric model, where if instances are close to each other, the response variable may have similar values. When training data is scarce or this relationship is already known, models with assumptions may be more useful than non-parametric models.
Using KNN for Classification
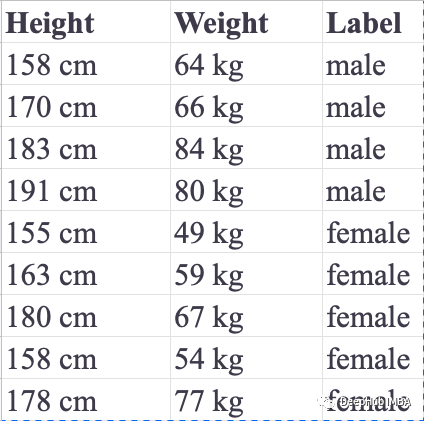
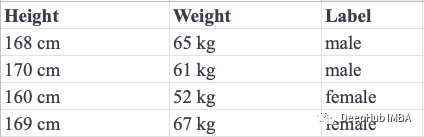
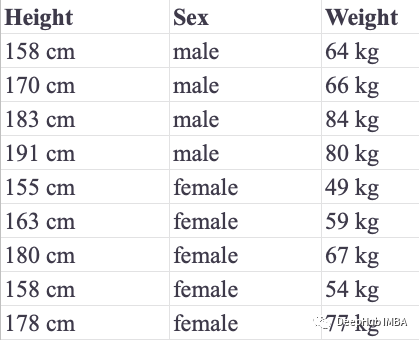
We use a simple problem where we need to predict a person’s gender based on their height and weight. There are two labels that can be assigned to the response variable, which is why this problem is called binary classification. The following table records nine training instances:
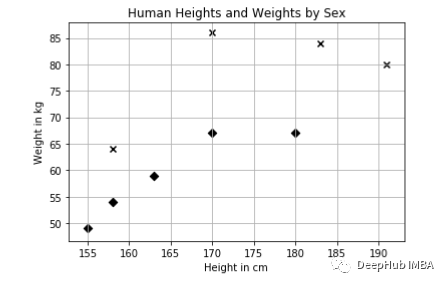
KNN can use an unlimited number of features, but visualizing more than three features is not possible (this is because we live in a 3D space and cannot visualize data in more dimensions). By creating scatter plots, we can visualize the data using matplotlib:
From the graph, it can be seen that males tend to be taller and heavier than females, as indicated by the x markers. Our experience also aligns with this observation. To predict a person’s gender based on their height and weight, we need to define a distance metric: we will measure the Euclidean distance between two points. In two-dimensional space, the Euclidean distance is calculated as follows:
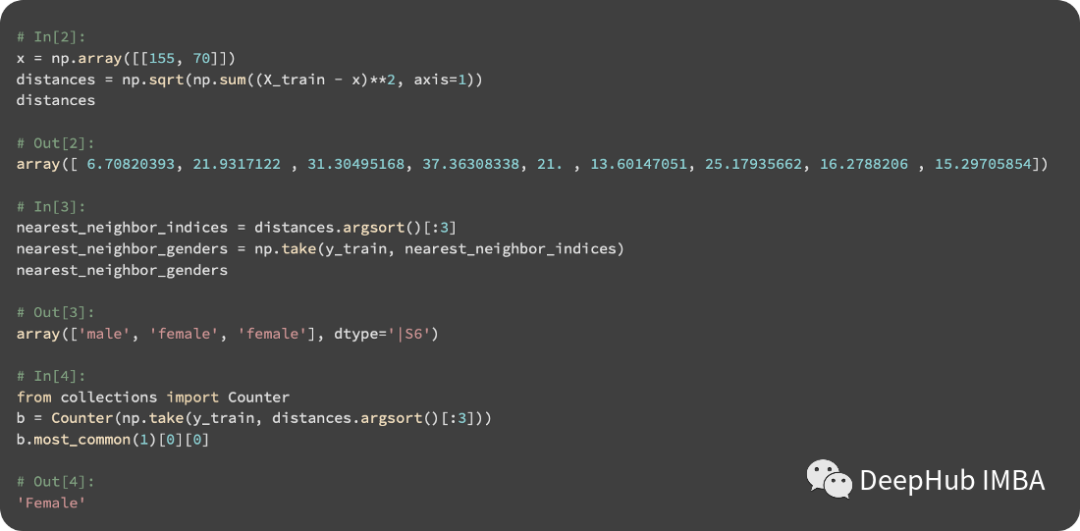
The next step is to calculate the distance between the query instance and all training instances:
Setting k to 3, we will choose the three nearest instances for prediction. In the script below, we calculate the distances between the test and training instances and determine the most common gender among the neighbors:
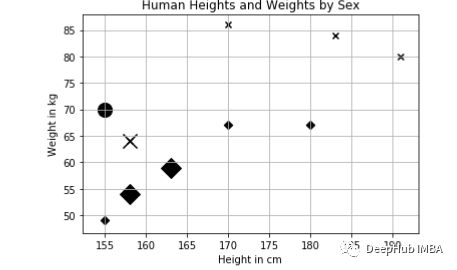
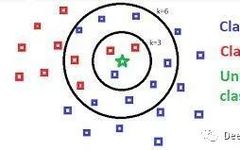
In the following figure, the circle represents the query instance, and the enlarged markers represent its three nearest neighbors:
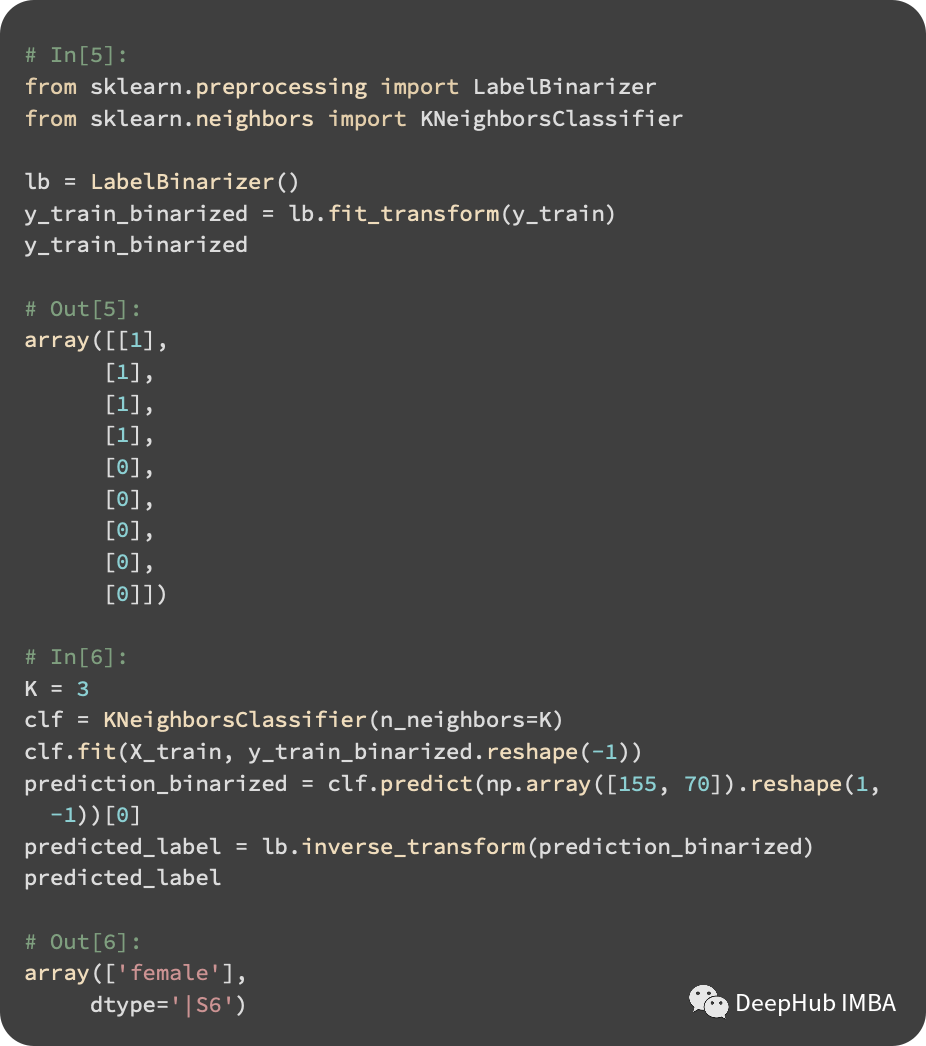
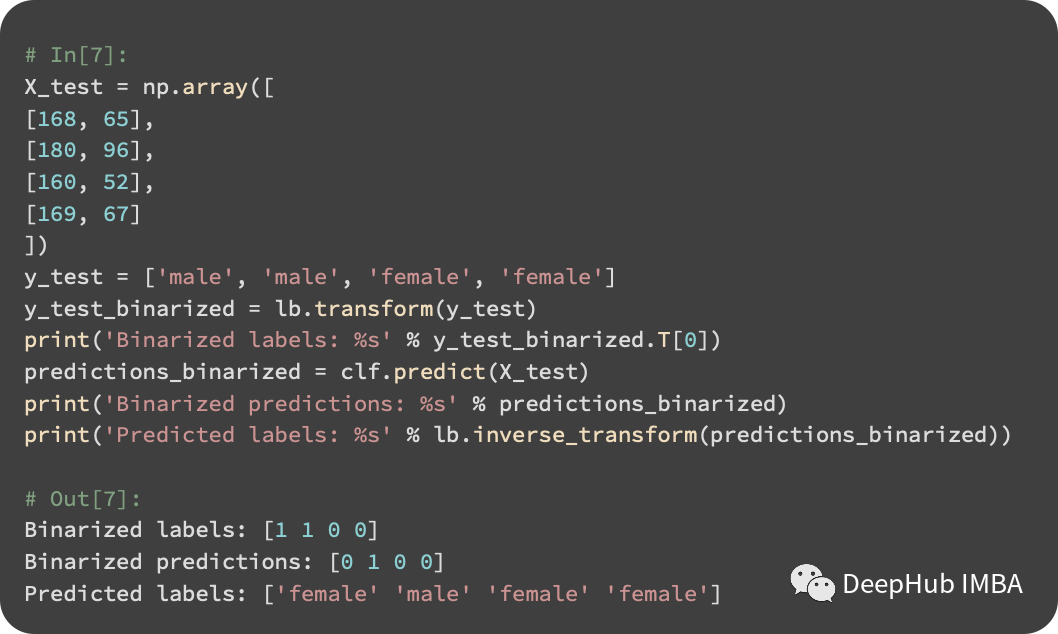
There are two female neighbors and one male neighbor. Therefore, the result for our test instance is female. The KNN classifier is implemented using scikit-learn, and the code is as follows:
LabelBinarizer first converts strings to integers, and the fit method creates a mapping from label strings to integers. The input labels are transformed using the transform method. The fit_transform method calls both fit and transform at the same time. If the training and test sets are independently transformed, then in the training set, males may map to 1, while in the test set, they may map to 0. Thus, we use the object from the training set for fitting. Then we use KNeighborsClassifier for prediction.
By comparing our test labels with the classifier’s predictions, we find that a male test instance was incorrectly predicted as female. Thus, our accuracy is 75%:
Using KNN for Regression
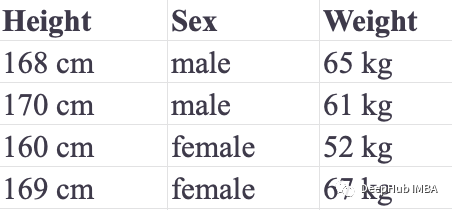
KNN can also perform regression analysis. Let’s use their height and gender to predict their weight. We have listed our training and test sets in the table below:
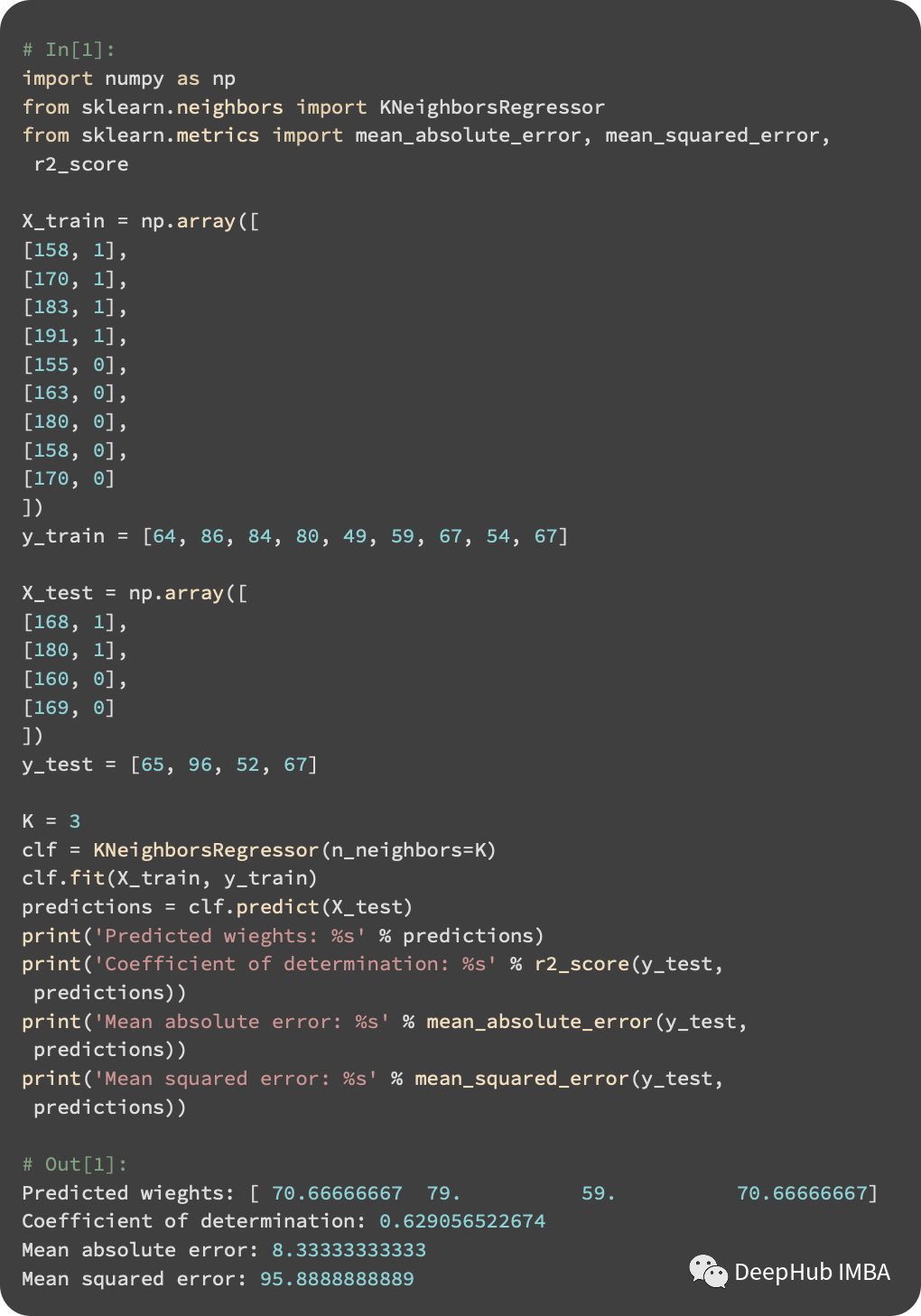
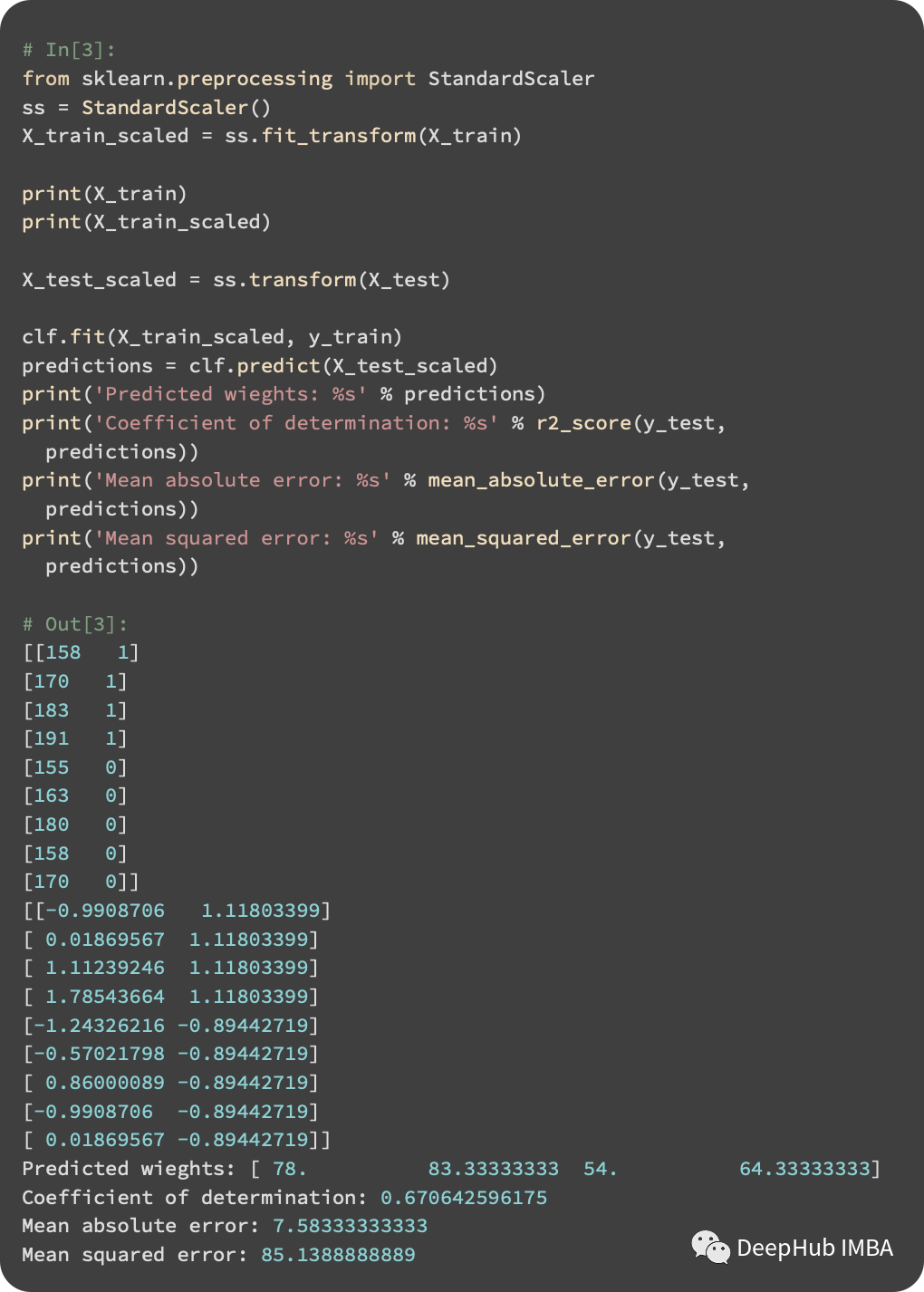
Using KNeighborsRegressor, we can perform regression tasks. Here, the two performance metrics for the regression task are: Mean Absolute Error (MAE) and Mean Squared Error (MSE).
The calculation method for MAE is to take the average of the absolute values of the prediction errors. The calculation method for MAE is as follows:
Compared to Mean Absolute Error, Mean Squared Error (MSE) is more commonly used. MSE can be calculated by averaging the squares of the prediction errors, as shown in the formula below:
MSE is more sensitive to outliers than MAE; generally, ordinary linear regression minimizes the square root of MSE:
By standardizing the data, our model performs better. When a person’s gender is included in the distance between instances, the model can make better predictions.
Conclusion
KNN is a simple yet powerful classification and regression model introduced in this article. The KNN model is a lazy non-parametric learning model; its parameters are not estimated based on training data. To predict the response variable, it stores all training instances and uses the closest instances for testing. In Sklearn, we can directly call built-in methods to use it.