Click on the above “Beginner’s Guide to Vision“, select to add “Star” or “Pin“

Introduction
The idea of KNN (k-Nearest Neighbors) is simple, and the mathematical knowledge required is almost zero, making it very practical as an introduction to machine learning. It can explain many details during the use of machine learning algorithms and provide a more complete characterization of the machine learning application process.
First, let’s briefly introduce the idea of KNN. Suppose we have two types of datasets, one represented by red points and the other by blue points. These two types of points serve as our training dataset. When a new data point, represented by a green point, arrives, how do we classify this green point?
Generally, we first need to specify a value for k. When a new data point arrives, we first calculate the distance from this new data point to each data point in the training set, usually using the Euclidean distance.
Then we select the k nearest points from this set, where k is typically chosen as an odd number to facilitate later voting decisions. Among the k points, we determine which class the new data belongs to based on the majority vote.

Basics of KNN
1. First, create the dataset x_train, y_train, and a new data point x_new, and visualize it using matplotlib.
import numpy as np
import matplotlib.pyplot as plt
raw_data_x = [[3.3935, 2.3313], [3.1101, 1.7815], [1.3438, 3.3684], [3.5823, 4.6792], [2.2804, 2.8670], [7.4234, 4.6965], [5.7451, 3.5340], [9.1722, 2.5111], [7.7928, 3.4241], [7.9398, 0.7916]]
raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
x_train = np.array(raw_data_x)
y_train = np.array(raw_data_y)
x_new = np.array([8.0936, 3.3657])
plt.scatter(x_train[y_train==0,0], x_train[y_train==0,1], color='g')
plt.scatter(x_train[y_train==1,0], x_train[y_train==1,1], color='r')
plt.scatter(x_new[0], x_new[1], color='b')
plt.show()1. KNN process
2. Calculate distances
from math import sqrt
distance = []
for x in x_train:
d = sqrt(np.sum((x_new - x) ** 2))
distance.append(d)
# Actually, the above code can be simplified to one line
# distances = [sqrt(np.sum((x_new - x) ** 2)) for x in x_train]Output:
[10.888422144185997, 11.825242797930196, 15.18734646375067, 11.660703691887552, 12.89974598548359, 12.707715895864213, 9.398411207752083, 15.62480440229573, 12.345673749536719, 14.394770082568183]Sort the distances and return the sorted index positions.
nearest = np.argsort(distances)Output: array([6, 0, 3, 1, 8, 5, 4, 9, 2, 7], dtype=int64)
Take the k nearest points, assume k=5.
k = 5
topk_y = [y_train[i] for i in nearest[:k]]
topk_yOutput: [1, 0, 0, 0, 1]
From the output, we can see that among the 5 nearest points, three points belong to the first class and two points belong to the second class. According to the majority rule, the new data point belongs to the first class!
Voting
from collections import Counter
Counter(topk_y)Output: Counter({1: 2, 0: 3})
votes = Counter(topk_y)
votes.most_common(1)
y_new = votes.most_common(1)[0][0]Output: 0
Thus, we have completed a basic KNN!
Write your own KNN function
KNN is a machine learning algorithm that does not require a training process. Its dataset can be approximated as a model.
import numpy as np
from math import sqrt
from collections import Counter
def kNN_classifier(k, x_train, y_train, x_new):
assert 1 <= k <= x_train.shape[0], "k must be valid"
assert x_train.shape[0] == y_train.shape[0], "the size of x_train must be equal to the size of y_train"
assert x_train.shape[1] == x_new.shape[0], "the feature number of x_new must be equal to x_train"
distances = [sqrt(np.sum((x_new - x) ** 2)) for x in x_train]
nearest = np.argsort(distances)
topk_y = [y_train[i] for i in nearest[:k]]
votes = Counter(topk_y)
return votes.most_common(1)[0][0]Let’s test it:
raw_data_x = [[3.3935, 2.3313], [3.1101, 1.7815], [1.3438, 3.3684], [3.5823, 4.6792], [2.2804, 2.8670], [7.4234, 4.6965], [5.7451, 3.5340], [9.1722, 2.5111], [7.7928, 3.4241], [7.9398, 0.7916]]
raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
x_train = np.array(raw_data_x)
y_train = np.array(raw_data_y)
x_new = np.array([8.0936, 3.3657])
y_new = kNN_classifier(5, x_train, y_train, x_new)
print(y_new)Using KNN from sklearn
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
raw_data_x = [[3.3935, 2.3313], [3.1101, 1.7815], [1.3438, 3.3684], [3.5823, 4.6792], [2.2804, 2.8670], [7.4234, 4.6965], [5.7451, 3.5340], [9.1722, 2.5111], [7.7928, 3.4241], [7.9398, 0.7916]]
raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
x_train = np.array(raw_data_x)
y_train = np.array(raw_data_y)
x_new = np.array([8.0936, 3.3657])
knn_classifier = KNeighborsClassifier(n_neighbors=5)
knn_classifier.fit(x_train, y_train)
y_new = knn_classifier.predict(x_new.reshape(1, -1))
print(y_new[0])Write an object-oriented KNN
import numpy as np
from math import sqrt
from collections import Counter
class KNNClassifier():
def __init__(self, k):
assert 1 <= k, "k must be valid"
self.k = k
self._x_train = None
self._y_train = None
def fit(self, x_train, y_train):
assert x_train.shape[0] == y_train.shape[0],
"the size of x_train must be equal to the size of y_train"
assert self.k <= x_train.shape[0],
"the size of x_train must be at least k"
self._x_train = x_train
self._y_train = y_train
return self
def predict(self, x_new):
x_new = x_new.reshape(1, -1)
assert self._x_train is not None and self._y_train is not None,
"must fit before predict"
assert x_new.shape[1] == self._x_train.shape[1],
"the feature number of x must be equal to x_train"
y_new = [self._predict(x) for x in x_new]
return np.array(y_new)
def _predict(self, x):
assert x.shape[0] == self._x_train.shape[1],
"the feature number of x must be equal to x_train"
distances = [sqrt(np.sum((x_train - x) ** 2)) for x_train in self._x_train]
nearest = np.argsort(distances)
topk_y = [self._y_train[i] for i in nearest[:self.k]]
votes = Counter(topk_y)
return votes.most_common(1)[0][0]
def __repr__(self):
return "KNN(k=%d)" % self.kLet’s test it:
raw_data_x = [[3.3935, 2.3313], [3.1101, 1.7815], [1.3438, 3.3684], [3.5823, 4.6792], [2.2804, 2.8670], [7.4234, 4.6965], [5.7451, 3.5340], [9.1722, 2.5111], [7.7928, 3.4241], [7.9398, 0.7916]]
raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
x_train = np.array(raw_data_x)
y_train = np.array(raw_data_y)
x_new = np.array([8.0936, 3.3657])
knn_clf = KNNClassifier(6)
knn_clf.fit(x_train, y_train)
y_new = knn_clf.predict(x_new)
print(y_new[0])Splitting the dataset
import numpy as np
from sklearn import datasets
def train_test_split(x, y, test_ratio=0.2, seed=None):
assert x.shape[0] == y.shape[0], "the size of x must be equal to the size of y"
assert 0.0 <= test_ratio <= 1.0, "test_ratio must be valid"
if seed: np.random.seed(seed)
shuffle_idx = np.random.permutation(len(x))
test_size = int(len(x) * test_ratio)
test_idx = shuffle_idx[:test_size]
train_idx = shuffle_idx[test_size:]
x_train = x[train_idx]
y_train = y[train_idx]
x_test = x[test_idx]
y_test = y[test_idx]
return x_train, y_train, x_test, y_testTesting KNN with Iris Dataset in sklearn
import numpy as np
from sklearn import datasets
x = datasets.load_iris().data
y = datasets.load_iris().target
x_train, y_train, x_test, y_test = train_test_split(x, y)
my_knn_clf = KNNClassifier(k=3)
my_knn_clf.fit(x_train, y_train)
y_predict = my_knn_clf.predict(x_test)
print(sum(y_predict == y_test))
print(sum(y_predict == y_test) / len(y_test))
# You can also use sklearn's built-in dataset splitting method
from sklearn.model_selection import train_test_split
import numpy as np
from sklearn import datasets
x = datasets.load_iris().data
y = datasets.load_iris().target
x_train, y_train, x_test, y_test = train_test_split(x, y,
test_size=0.2, random_state=666)
my_knn_clf = KNNClassifier(k=3)
my_knn_clf.fit(x_train, y_train)
y_predict = my_knn_clf.predict(x_test)
print(sum(y_predict == y_test))
print(sum(y_predict == y_test) / len(y_test))Testing KNN with Handwritten Digits Dataset in sklearn
First, let’s understand the handwritten digits dataset.
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
digits = datasets.load_digits()
digits.keys()
print(digits.DESCR)
y.shape
digits.target_names
y[:100]
x[:10]
some_digit = x[666]
y[666]
some_digit_image = some_digit.reshape(8, 8)
plt.imshow(some_digit_image, cmap=plt.cm.binary)
plt.show()Next, let’s try it out.
from sklearn import datasets
from shuffle_dataset import train_test_split
from knn_clf import KNNClassifier
digits = datasets.load_digits()
x = digits.data
y = digits.target
x_train, y_train, x_test, y_test = train_test_split(x, y, test_ratio=0.2)
my_knn_clf = KNNClassifier(k=3)
my_knn_clf.fit(x_train, y_train)
y_predict = my_knn_clf.predict(x_test)
print(sum(y_predict == y_test) / len(y_test))Wrap the accuracy calculation into a function for easy calling.
def accuracy_score(y_true, y_predict):
assert y_true.shape[0] == y_predict.shape[0],
"the size of y_true must be equal to the size of y_predict"
return sum(y_true == y_predict) / len(y_true)Then encapsulate it into the KNNClassifier class.
import numpy as np
from math import sqrt
from collections import Counter
from metrics import accuracy_score
class KNNClassifier():
def __init__(self, k):
assert 1 <= k, "k must be valid"
self.k = k
self._x_train = None
self._y_train = None
def fit(self, x_train, y_train):
assert x_train.shape[0] == y_train.shape[0],
"the size of x_train must be equal to the size of y_train"
assert self.k <= x_train.shape[0],
"the size of x_train must be at least k"
self._x_train = x_train
self._y_train = y_train
return self
def predict(self, x_new):
# x_new = x_new.reshape(1, -1)
assert self._x_train is not None and self._y_train is not None,
"must fit before predict"
assert x_new.shape[1] == self._x_train.shape[1],
"the feature number of x must be equal to x_train"
y_new = [self._predict(x) for x in x_new]
return np.array(y_new)
def _predict(self, x):
assert x.shape[0] == self._x_train.shape[1],
"the feature number of x must be equal to x_train"
distances = [sqrt(np.sum((x_train - x) ** 2)) for x_train in self._x_train]
nearest = np.argsort(distances)
topk_y = [self._y_train[i] for i in nearest[:self.k]]
votes = Counter(topk_y)
return votes.most_common(1)[0][0]
def score(self, x_test, y_test):
y_predict = self.predict(x_test)
return accuracy_score(y_test, y_predict)
def __repr__(self):
return "KNN(k=%d)" % self.kIn fact, sklearn has already encapsulated these functionalities.
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
digits = datasets.load_digits()
x = digits.data
y = digits.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
knn_classifier = KNeighborsClassifier(n_neighbors=3)
knn_classifier.fit(x_train, y_train)
knn_classifier.score(x_test, y_test)Hyperparameters
k
When is the hyperparameter k optimal in KNN?
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
digits = datasets.load_digits()
x = digits.data
y = digits.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
best_score = 0.0
best_k = -1
for k in range(1, 11):
knn_clf = KNeighborsClassifier(n_neighbors=k)
knn_clf.fit(x_train, y_train)
score = knn_clf.score(x_test, y_test)
if score > best_score:
best_k = k
best_score = score
print("best k=", best_k)
print("best score=", best_score)Voting method
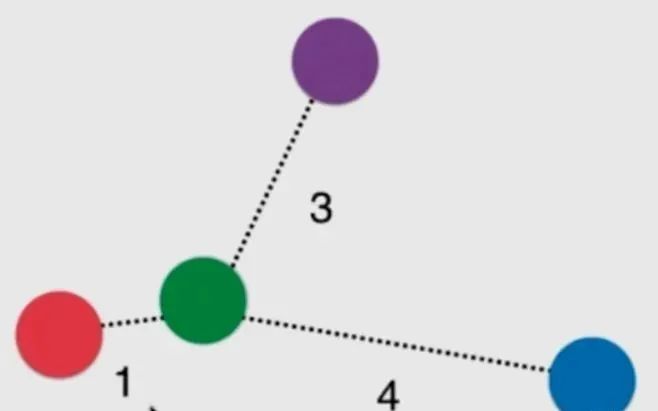
The above image shows that the three nearest points to the green ball are the red ball labeled 1, the purple ball labeled 3, and the blue ball labeled 4. If we only consider the majority vote among the k nearest neighbors, we currently have a tie.
Even if it’s not a tie, the red ball is still the closest to the green. At this point, we can consider adding weights to them. Generally, the inverse of the distance is used as the weight. Suppose the distances are 1, 3, and 4.
Red ball: 1 Purple + Blue: 1/3 + 1/4 = 7/12
Both have less weight than the red ball, so ultimately this green ball will be classified as red. This effectively solves the tie problem. Therefore, this is also considered a hyperparameter of KNN.
In fact, this issue has already been addressed in the KNeighborsClassifier in sklearn. In KNeighborsClassifier(n_neighbors=k, weights=?).
Another parameter is weights, which generally has two types: uniform and distance.
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
digits = datasets.load_digits()
x = digits.data
y = digits.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
best_method = ""
best_score = 0.0
best_k = -1
for method in["uniform", "distance"]:
for k in range(1, 11):
knn_clf = KNeighborsClassifier(n_neighbors=k, weights=method)
knn_clf.fit(x_train, y_train)
score = knn_clf.score(x_test, y_test)
if score > best_score:
best_method = method
best_k = k
best_score = score
print("best_method=", best_method)
print("best k=", best_k)
print("best score=", best_score)p
If using distance, there are many distance metrics that can be used, including Euclidean distance, Manhattan distance, and Minkowski distance.
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
digits = datasets.load_digits()
x = digits.data
y = digits.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
best_p = -1
best_score = 0.0
best_k = -1
for p in range(1, 6):
for k in range(1, 11):
knn_clf = KNeighborsClassifier(n_neighbors=k, weights="distance", p=p)
knn_clf.fit(x_train, y_train)
score = knn_clf.score(x_test, y_test)
if score > best_score:
best_p = p
best_k = k
best_score = score
print("best_p=", best_p)
print("best k=", best_k)
print("best score=", best_score)Download 1: OpenCV-Contrib Extension Module Chinese Tutorial
Reply "Extension Module Chinese Tutorial" in the backend of "Beginner's Guide to Vision" public account to download the first Chinese version of the OpenCV extension module tutorial, covering installation of extension modules, SFM algorithms, stereo vision, target tracking, biological vision, super-resolution processing, and more than twenty chapters of content.
Download 2: Python Vision Practical Project 52 Lectures
Reply "Python Vision Practical Project" in the backend of "Beginner's Guide to Vision" public account to download 31 visual practical projects including image segmentation, mask detection, lane detection, vehicle counting, eyeliner addition, license plate recognition, character recognition, emotion detection, text content extraction, face recognition, etc., to help quickly learn computer vision.
Download 3: OpenCV Practical Project 20 Lectures
Reply "OpenCV Practical Project 20 Lectures" in the backend of "Beginner's Guide to Vision" public account to download 20 practical projects based on OpenCV, achieving advanced learning of OpenCV.
Discussion Group
Welcome to join the reader group of the public account to exchange ideas with peers. Currently, there are WeChat groups for SLAM, 3D vision, sensors, autonomous driving, computational photography, detection, segmentation, recognition, medical imaging, GAN, algorithm competitions, etc. (will gradually be subdivided in the future). Please scan the WeChat ID below to join the group, noting: "Nickname + School/Company + Research Direction", for example: "Zhang San + Shanghai Jiaotong University + Visual SLAM". Please follow the format for remarks, otherwise, you will not be approved. After successful addition, you will be invited to the relevant WeChat group based on your research direction. Please do not send advertisements in the group, otherwise, you will be removed from the group. Thank you for your understanding~
