Beyond ReLU: The GELU Activation Function in BERT and GPT-2

At least in the field of NLP, GELU has become the choice of many industry-leading models.

As the “switch” that determines whether a neural network transmits information, the activation function is crucial for neural networks. However, is the ReLU commonly used today really the most efficient method? Recently, people on social networks have found a seemingly more powerful activation function: GELU, which was proposed as early as 2016, yet its paper has only been cited 34 times on Google Scholar to date.

In fact, GELU has already been adopted by many of the leading models today. According to incomplete statistics, BERT, RoBERTa, ALBERT, and other top NLP models in the industry all use this activation function. Additionally, in OpenAI’s well-known unsupervised pre-training model GPT-2, researchers used the GELU activation function in all encoder modules.

The authors of the GELU paper come from UC Berkeley and the Toyota Technological Institute at Chicago:

Paper link: https://arxiv.org/pdf/1606.08415.pdf

The Current Most Popular Activation Function ReLU

Before discussing GELU, let’s first review the currently most popular Rectified Linear Unit (ReLU), also known as the corrected linear unit. ReLU was researched by Vinod Nair from the University of Toronto and Turing Award winner Geoffrey Hinton, and it was accepted at the ICML 2010 conference.

ReLU is the most commonly used activation function in artificial neural networks (activation function), usually referring to a family of nonlinear functions represented by the “slope” function and its variants. This family of functions commonly includes ReLU and Leaky ReLU.

In a general sense, the linear rectifier function refers to the slope function in mathematics, namely:

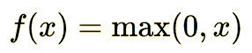
The function graph is as follows:

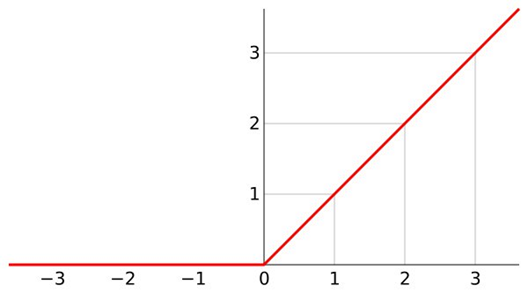
In neural networks, linear rectification as the activation function of neurons defines the nonlinear output result of that neuron after linear transformation. ReLU can combat the gradient explosion/vanishing problem, and is relatively efficient in computation. Since it was applied in the famous computer vision model AlexNet in 2012, ReLU has become popular and is now widely regarded as the best-performing activation function.

History of Activation Functions

Early artificial neurons used binary threshold units (Hopfield, 1982; McCulloch & Pitts, 1943). These difficult binary decisions were smoothed out using the Sigmoid activation function, allowing for very fast decoding speeds and training via backpropagation. However, as network depth increased, it was demonstrated that training using the Sigmoid activation function was less effective than using non-smooth, low-probability ReLU (Nair & Hinton, 2010), because ReLU makes gating decisions based on input signals.

Although ReLU lacks statistical significance, it remains a highly competitive engineering solution, converging faster and yielding better results than the Sigmoid activation function. Thanks to the success of ReLU, a recent improved version has emerged—the ELU function. This function allows nonlinear functions similar to ReLU to output negative values and enhance training speed. In summary, the choice of activation function is also an important part of neural network architecture design.

Deep nonlinear classifiers can fit the data well, forcing designers to face random regularization (such as adding noise in hidden layers) or adopting dropout mechanisms. These two choices are still separate from activation functions. Some random regularizations can make the network behave like a combination of many networks, thereby improving accuracy.

Thus, nonlinearity and dropout together determine the output of neurons, but these two innovations still have distinctions. Additionally, nonlinearity and dropout do not include each other, as popular random regularization is independent of input during execution, and nonlinearity also receives assistance from such regularization.

In this article, researchers propose a new nonlinear activation function called the Gaussian Error Linear Unit (GELU). GELU is related to random regularization because it is a correction expectation of adaptive Dropout (Ba & Frey, 2013). This indicates a higher probability of neuron output. Researchers found that models using the GELU activation function performed comparably or surpassed those using ReLU or ELU in tasks such as computer vision, natural language processing, and automatic speech recognition.

GELU Activation Function: A Mathematical Perspective

Researchers indicate that influenced by mechanisms like Dropout and ReLU, they aim to regularize “unimportant” activation information to zero. We can understand this as multiplying the input value by 1 or 0 based on its situation. A more “mathematical” description is that for each input x, which follows a standard normal distribution N(0, 1), it is multiplied by a Bernoulli distribution Bernoulli(Φ(x)), where Φ(x) = P(X ≤ x).

The lower x is, the higher the probability of it being regularized to zero. For ReLU, this threshold is 0; any input less than zero will be regularized to zero. This type of activation function retains both probabilistic characteristics and dependency on input.

Now, let’s take a look at what GELU actually looks like. We often desire neural networks to have deterministic decisions, and this idea gave rise to the GELU activation function. This function’s nonlinearity hopes to transform the random regularization term on input x, which sounds complex but can specifically be expressed as: Φ(x) × Ix + (1 − Φ(x)) × 0x = xΦ(x).

We can understand that for a portion of Φ(x), it directly multiplies the input x, while for another part (1 − Φ(x)), they need to be regularized to zero. Not strictly speaking, the above expressioncan scale x by how much it is larger than other inputs.

Because the Gaussian probability distribution function is usually calculated based on the loss function, researchers define the Gaussian Error Linear Unit (GELU) as:

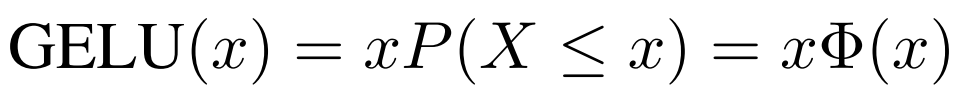
The above function cannot be directly computed, so it can be approximated through another method. The expression derived by the researchers is:

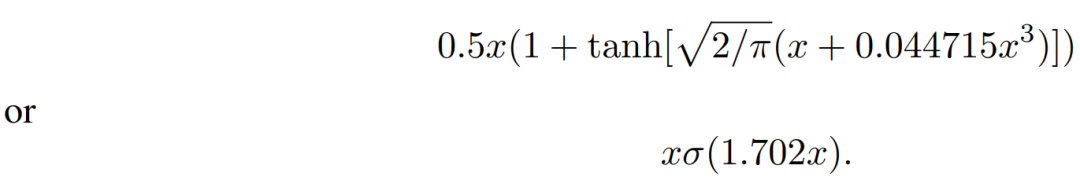
Although researchers state that the mean and variance of the Gaussian probability distribution function can be set to be trainable, they simply use a mean of 0 and a variance of 1. Seeing such an expression reminds one of the Swish activation function proposed by Google in 2017, which can be simply written as: f(x) = x · sigmoid(x).

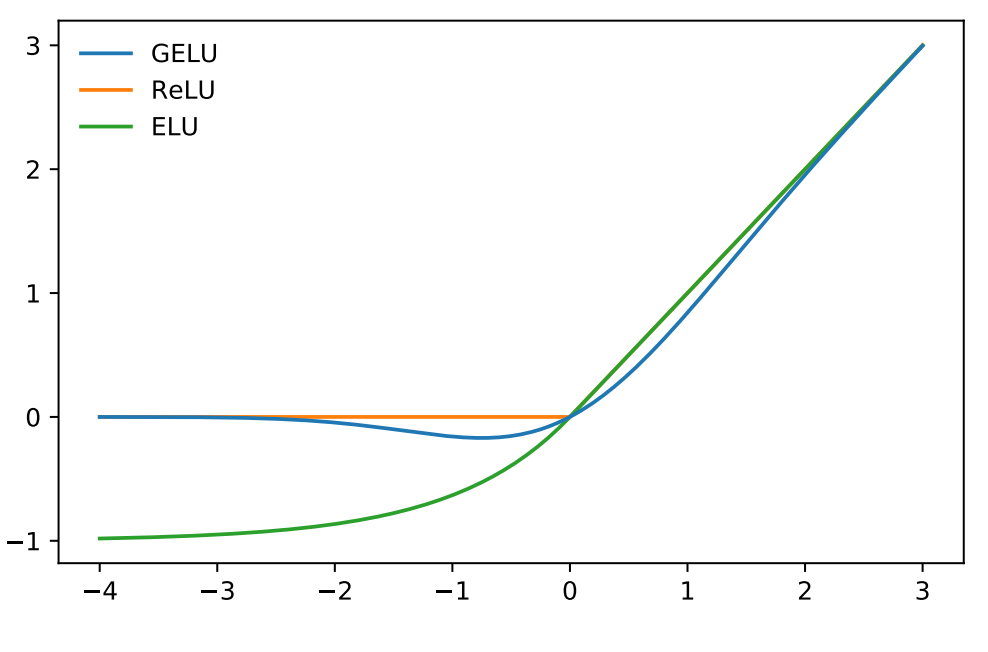Graph of the GELU activation function.

In the research of Quoc V. Le et al., they defined the Swish activation function as x · σ(βx), where σ() is the standard sigmoid function, and β can be a constant or a trainable parameter. Such activation functions are “searched” out, as researchers performed automatic searches among a series of function families and found that the Swish activation function performed the best.

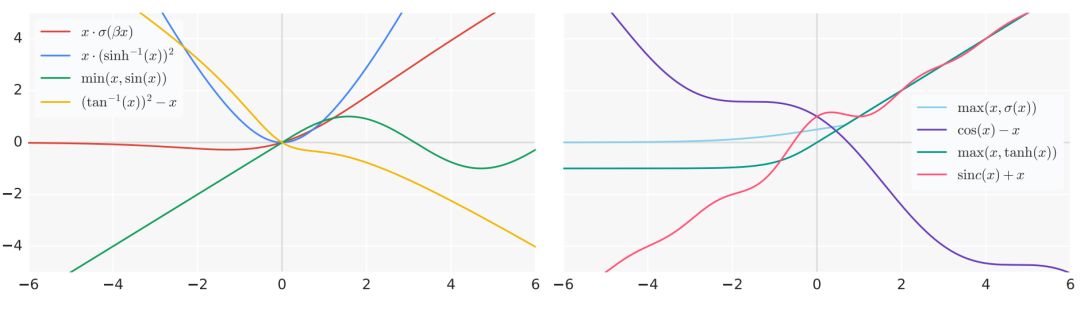
Through the searched activation functions, they all performed quite well, selected from arXiv: 1710.05941.

Performance Comparison: GELU vs ReLU

Researchers compared the performance of GELU with ReLU and ELU activation functions. They chose the following tasks:

• MNIST image classification (10 classes, 60,000 training images and 10,000 test images);

• TIMIT speech recognition (3,696 training samples, 1,152 validation samples, and 192 test samples);

• CIFAR-10/100 classification (10/100 classes, 50,000 training samples and 10,000 test samples).

MNIST Image Classification Task

Researchers tested the MNIST classification task in a fully connected network, where the parameters for GELU were μ = 0, σ = 1. ELU had α = 1. Each network had 8 layers and 128 neurons.

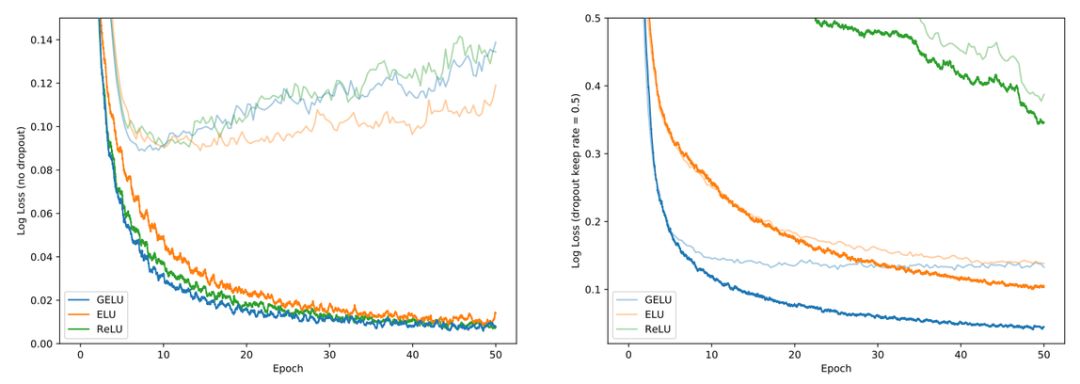
Figure 2 left:No dropout model, Figure right:Model set dropout to 0.5.

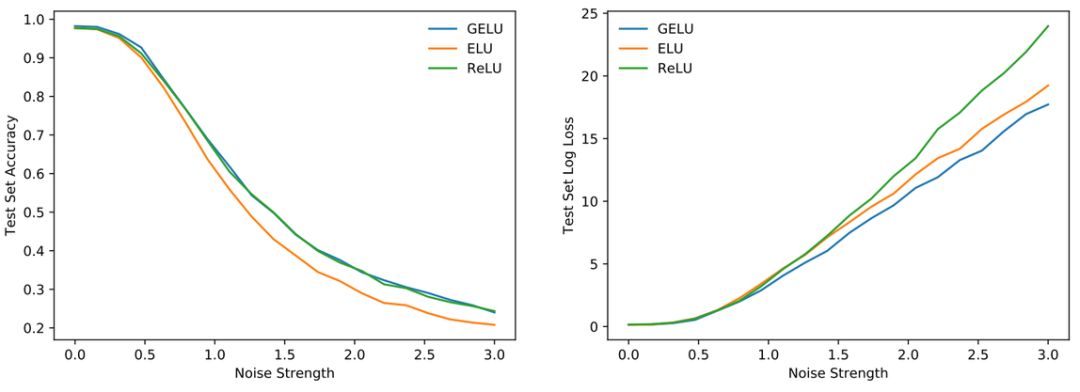
Figure 3:MNIST robustness results.

TIMIT Speech Recognition Task

Another challenge researchers faced was using the TIMIT dataset for phoneme recognition, which contains recordings of 680 speakers in a silent environment. The system is a wide classifier with 2,048 neurons and 5 layers (Mohamed et al., 2012), containing 39 output speech labels.

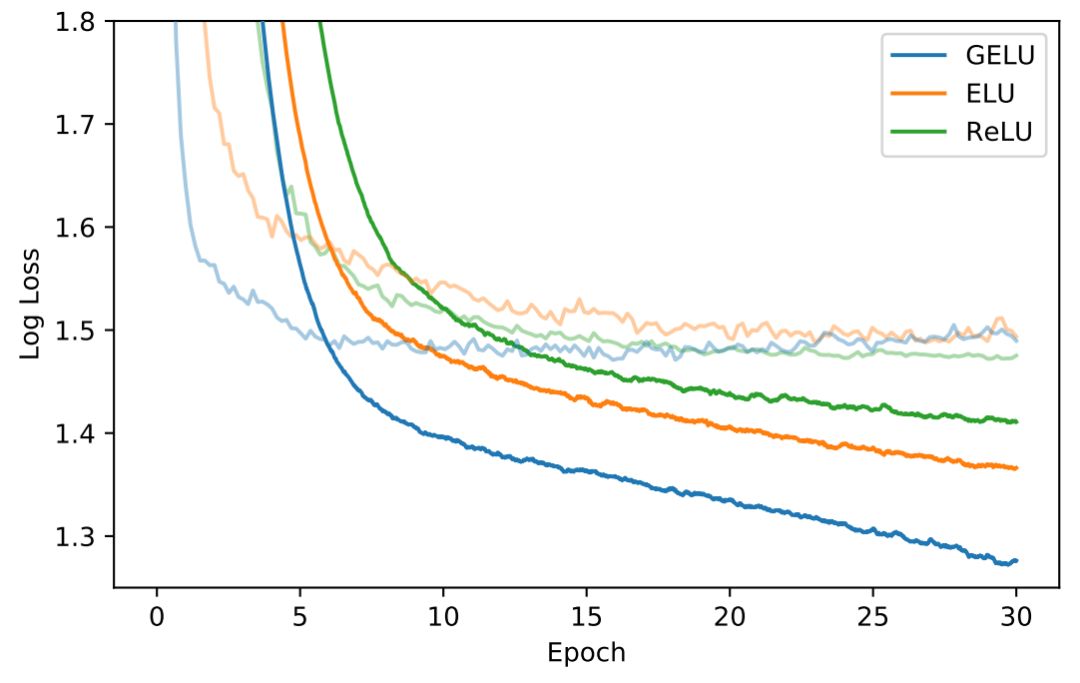
Figure 5:TIMIT speech recognition variation curve.

CIFAR-10/100 Classification Task

Researchers used 5,000 validation samples to fine-tune the initial learning rate {10^−3,10^−4,10^−5}, and then trained again on the entire training set based on the cross-validated learning rate. They optimized using Adam for 200 epochs, and the learning rate decayed to zero at epoch 100. As shown in Figure 6, each curve represents the median of three run results.

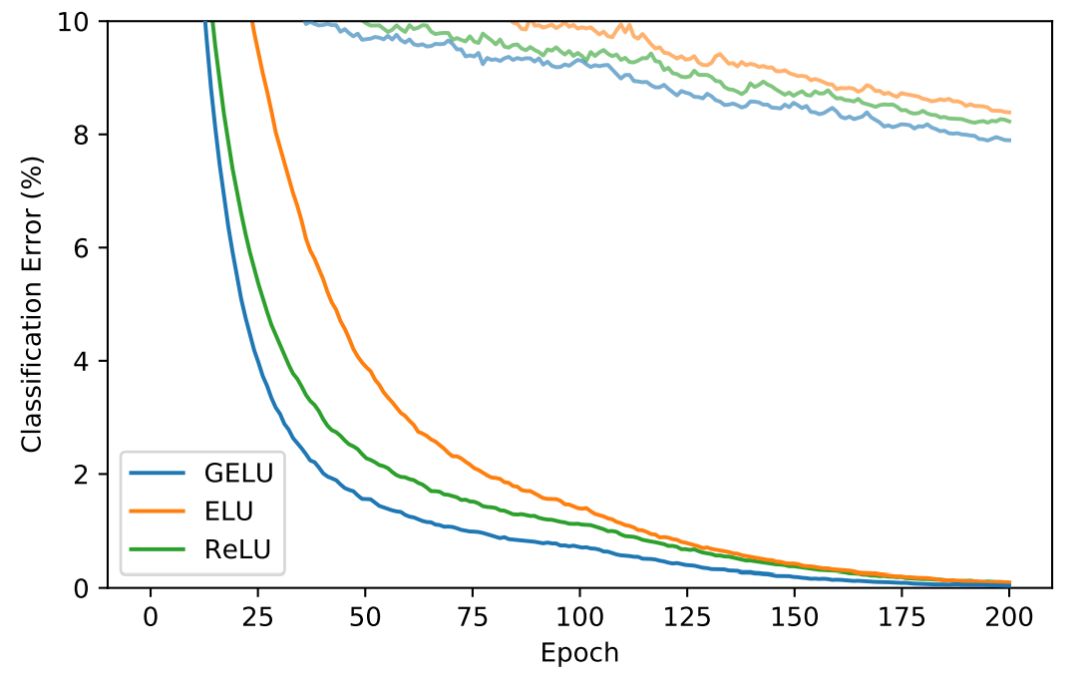
Figure 6:Results on the CIFAR-10 dataset.

Performance Comparison: GELU vs Swish

Because the expressions are quite similar, one has a fixed coefficient of 1.702, while the other has a variable coefficient β, the properties and effects of Swish and GELU are very similar. In the Swish paper (SEARCHING FOR ACTIVATION FUNCTIONS), researchers compared the effects of different activation functions, and we can see that Swish performs slightly better in visual or language tasks.

For example, when training Inception-ResNet-v2 on ImageNet, Swish slightly outperformed GELU, with each evaluation value recording results from three runs.

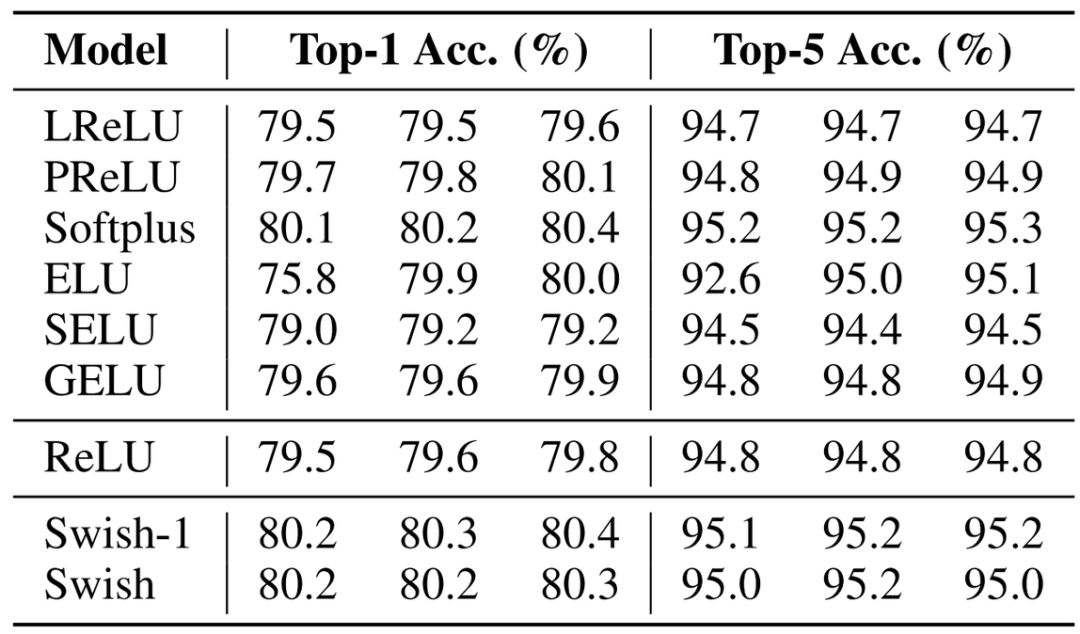
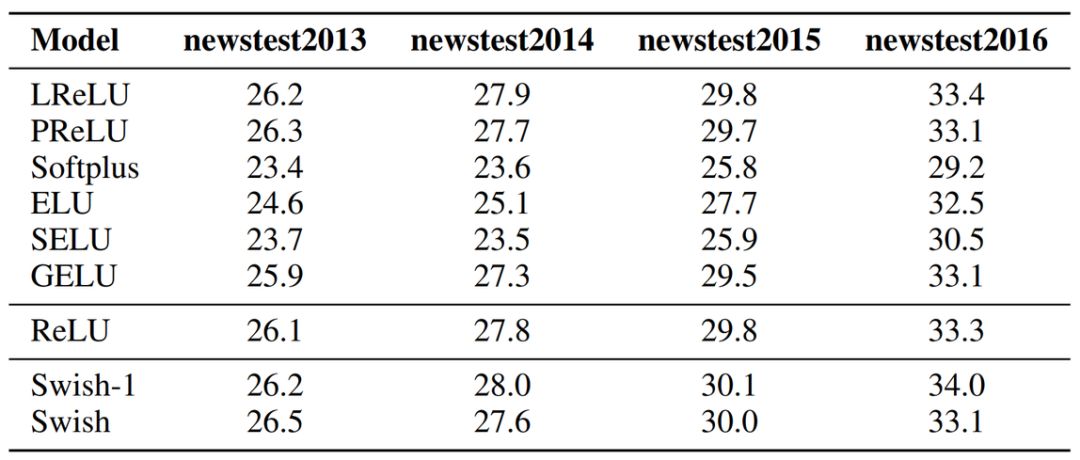
In machine translation tasks, researchers tested the effects of a 12-layer Transformer on the WMT 2014 English→German dataset. In different test sets, it seems that the Swish activation function is the best, although GELU also performs well, with only a small difference between them.

Finally, we found a large number of sequence modeling papers that used GELU as the activation function, whether in language modeling or acoustic modeling. Perhaps previously, sequence modeling commonly used tanh() rather than ReLU() as the activation function, and after discovering a better choice, more researchers attempted to adopt this nonlinear unit.

As mentioned earlier, there are two approximate implementations of GELU, one using tanh() and the other using σ(). We also found in the official GPT-2 code that more researchers adopted the tanh() implementation, even though it appears to be much more complex than xσ(1.702x).

# GPT-2's GELU implementation
def gelu(x):
    return 0.5*x*(1+tf.tanh(np.sqrt(2/np.pi)*(x+0.044715*tf.pow(x, 3))))

Regardless, as the most fundamental module of neural networks, we always hope for more innovations and perspectives beyond ReLU, GELU, and Swish.