Click above
Datartisan Data Craftsman
You can subscribe!
Artificial Neural Networks (ANN) are algorithms developed based on the brain’s processing mechanism to establish complex patterns and predictive problems.
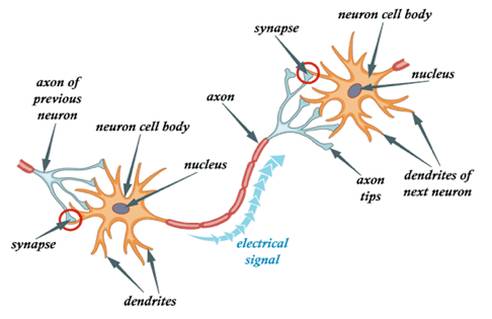
First, let’s understand how the brain processes information:
In the brain, there are billions of neuron cells that process information in the form of electrical signals. External information or stimuli are received by the dendrites of the neurons, processed in the cell body, transformed into output, and transmitted to the next neuron through the axon. The next neuron can choose to accept or reject it, depending on the strength of the signal.
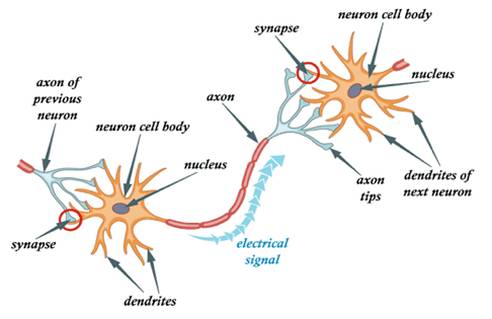

Now, let’s try to understand how ANN works:
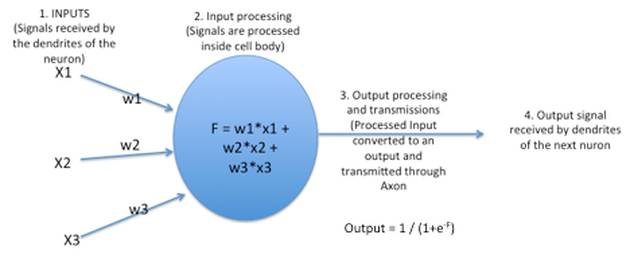
Here, $w_1$, $w_2$, and $w_3$ represent the strength of the input signals.
From the above, it can be seen that ANN is a very simple representation of how brain neurons work.
To clarify things, let’s use a simple example to understand ANN: A bank wants to assess whether to approve a loan application for a customer, so it wants to predict whether a customer is likely to default on the loan. It has the following data:
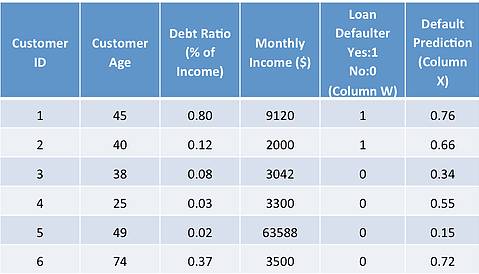
So, it must predict column X. A prediction value closer to 1 indicates that the customer is more likely to default.
Based on the neural structure of the example above, let’s try to create an artificial neural network structure:
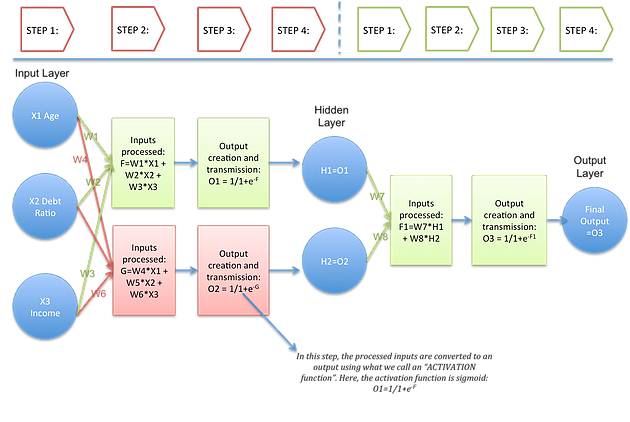
Typically, the simple ANN structure in the above example can be:
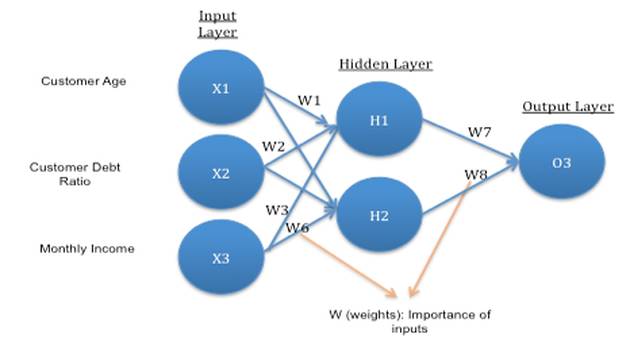
Key points related to the structure:
1. The network architecture has an input layer, one or more hidden layers, and an output layer. Due to its multi-layer structure, it is also referred to as MLP (Multi-Layer Perceptron).
2. The hidden layer can be seen as a ‘refinement layer’ that extracts important patterns from the input and passes them to the next layer. By identifying important information from the input that omits redundant information, the network becomes faster and more efficient.
3. The activation function has two obvious purposes:
It captures the nonlinear relationships between inputs.
It helps convert inputs into more useful outputs. In the above example, the activation function used is sigmoid: $$O_1=1+e^{-F}$$ where $F=W_1*X_1+W_2*X_2+W_3*X_3$. The sigmoid activation function creates an output between 0 and 1. There are other activation functions such as Tanh, softmax, and RELU.
4. Similarly, the hidden layer leads to the final prediction of the output layer:
$$O_3=1+e^{-F_1}$$ where $F_1=W_7*H_1+W_8*H_2$. Here, the output value ($O_3$) is between 0 and 1. Values close to 1 (e.g., 0.75) indicate a higher likelihood of customer default.
5. The weights W are significantly related to the inputs. If $w_1$ is 0.56 and $w_2$ is 0.92, then when predicting $H_1$, $X_2$: Debt Ratio is more important than $X_1$: Age.
6. The network architecture mentioned above is called a ‘feedforward network’, where input signals are only transmitted in one direction (from input to output). A ‘feedback network’ can be created where signals are transmitted in both directions.
7. A high-precision model provides predictions very close to the actual values. Therefore, in the above table, the column X values should be very close to the column W values. The prediction error is the difference between column W and column X:
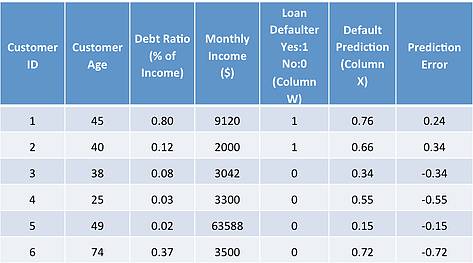
1. The key to obtaining a good model with accurate predictions is finding the optimal values of weights W that minimize prediction error. This is called the ‘backpropagation algorithm’, which makes ANN a learning algorithm because the model improves by learning from errors.
2. The most common method of backpropagation is called ‘gradient descent’, which uses iterative different values of W and evaluates the prediction error. Thus, to obtain the optimal W value, the W values vary within a small range, and the impact on the prediction error is assessed. Finally, these values of W are chosen as optimal, and as W continues to change, the error does not decrease further. To understand gradient descent in more detail, please refer to: http://www.kdnuggets.com/2017/04/simple-understand-gradient-descent-algorithm.html
Key Advantages of Neural Networks:
ANN has several key advantages that make them suitable for certain problems and situations:
ANN has the ability to learn and build models of nonlinear complex relationships, which is very important because many relationships between inputs and outputs in real life are nonlinear and complex.
ANN can generalize; after learning from initialized inputs and their relationships, it can also infer unknown relationships between unknown data, allowing the model to generalize and predict unknown data.
Unlike many other predictive techniques, ANN imposes no restrictions on input variables (e.g., how they are distributed). Moreover, many studies have shown that ANN can better model heteroscedasticity, i.e., data with high volatility and unstable variance, because it has the ability to learn hidden relationships in the data without imposing any fixed relationships in the data. This is very useful in financial time series forecasting (e.g., stock prices) where data fluctuates greatly.
Applications:
1. Image processing and character recognition: ANN has the ability to receive many inputs and process them to infer hidden, complex nonlinear relationships, playing an important role in image and character recognition. Handwritten character recognition has many applications in fraud detection (e.g., bank fraud) and even national security assessments. Image recognition is an evolving field widely used in facial recognition in social media, stagnation in cancer treatment in medicine, and satellite image processing for agricultural and defense purposes. Currently, research on ANN paves the way for deep neural networks, which are the foundation of ‘deep learning’, leading to a series of exciting innovations in areas like computer vision, speech recognition, and natural language processing, such as self-driving cars.
2. Forecasting: In economics and monetary policy, finance and stock markets, and daily business decisions (e.g., sales, financial distribution among products, capacity utilization), forecasting is generally required. More commonly, forecasting problems are complex; for instance, predicting stock prices is a complex problem with many potential factors (some known, some unknown). Considering these complex nonlinear relationships, traditional forecasting models have limitations. Given its ability to model and extract unknown features and relationships, ANN can provide a powerful alternative when applied correctly. Additionally, unlike these traditional models, ANN does not impose any restrictions on input and residual distributions. More research is ongoing, such as advancements in using LSTM and RNN for forecasting.
ANN is a powerful model with wide applications. The above lists several prominent examples, but they are widely applied in medicine, security, banking, finance, government, agriculture, and defense.
To learn ANNs in more detail, register for the 8-week Data Science course on www.deeplearningtrack.com – next batch starting soon.

More courses and articles are available on WeChat:
“Datartisan Data Craftsman”