A Brief History of Bayesian Neural Networks

Selected from NIPS 2016

Translated by Machine Heart

Contributors: Du Xia De, Cao Rui

At the recently concluded NIPS 2016 conference, Professor Zoubin Ghahramani from the University of Cambridge shared with us the development history of Bayesian neural networks. This article introduces the origin, golden age, and later revival of Bayesian neural networks from the perspective of research background and application issues, along with several key studies from each development stage, providing a concise learning resource that helps you quickly understand Bayesian neural networks.

P4: Research Background in the 1980s

• The “Boltzmann Machine” was published in 1985, followed by the publication of the backpropagation network paper in 1986, and then the emergence of PDP in 1987. This field was previously referred to as connection mechanisms, with NIPS being the main academic conference in this area.

P5-P7: Introduction to Neural Networks and Deep Learning

• Neural networks and deep learning systems perform excellently on many benchmark tasks, but they also have the following drawbacks:

• Require large amounts of data (often millions of samples)

• High computational cost for training and deployment (cloud GPU resources)

• Poor representation of uncertainty

• Often deceived by adversarial samples

• Very picky about optimization: non-convex + architecture selection, learning procedures, initialization, etc., requiring expert knowledge and experimentation

• Processes are black boxes, lack explanations, transparency, and are difficult to trust.

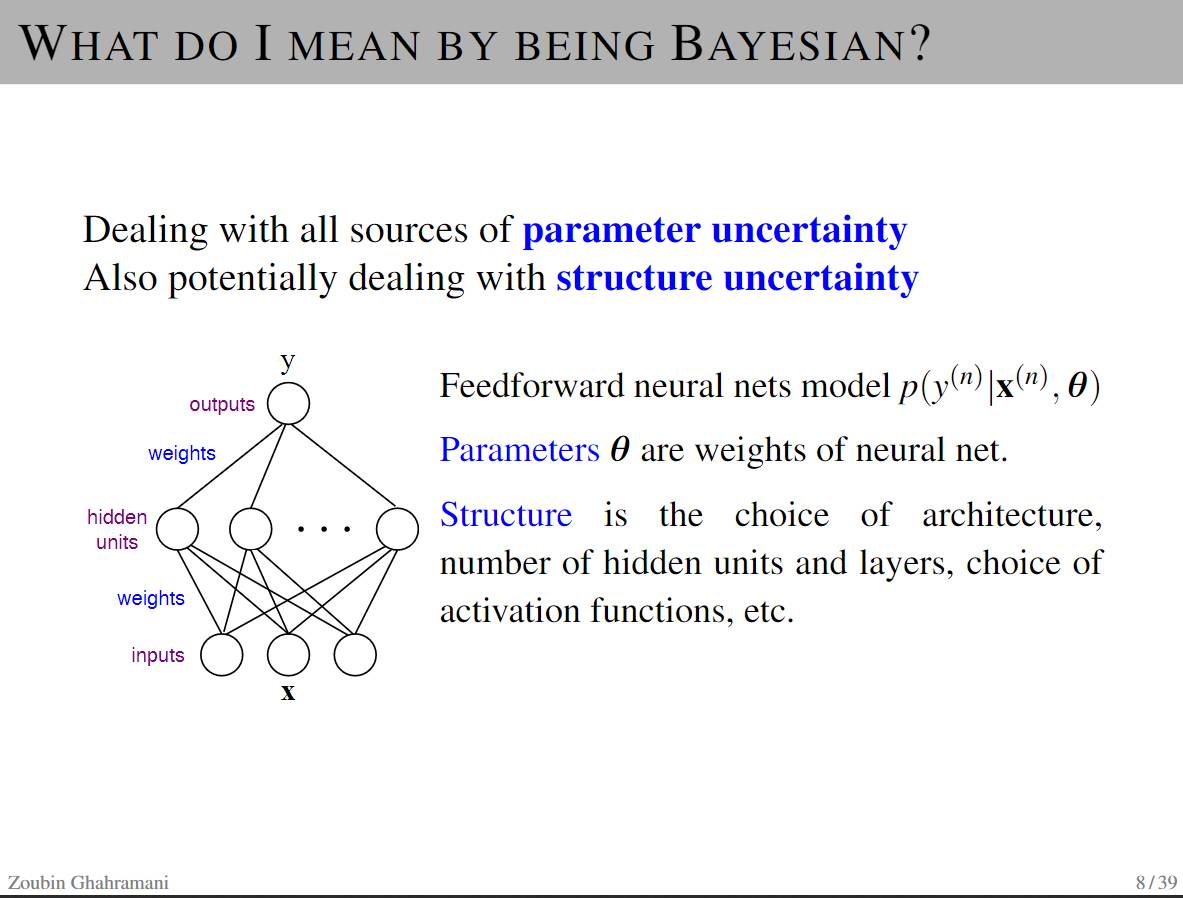
P8-12: How Bayesian Helps Here

• Handles all sources of parameter uncertainty

• Has the ability to handle structural uncertainty

• Bayesian theorem tells us to make inferences about hypotheses (uncertain quantities) from data (measurable quantities).

• Learning and prediction can be viewed as forms of inference.

• Calibrates model and predicts uncertainty: allows systems to know when they do not know.

• Automatic model complexity control and structure learning (Bayesian Occam’s Razor)

• It is important to note that “Bayesian” belongs to the category of algorithms, not models. Any well-defined model can be used with Bayesian methods.

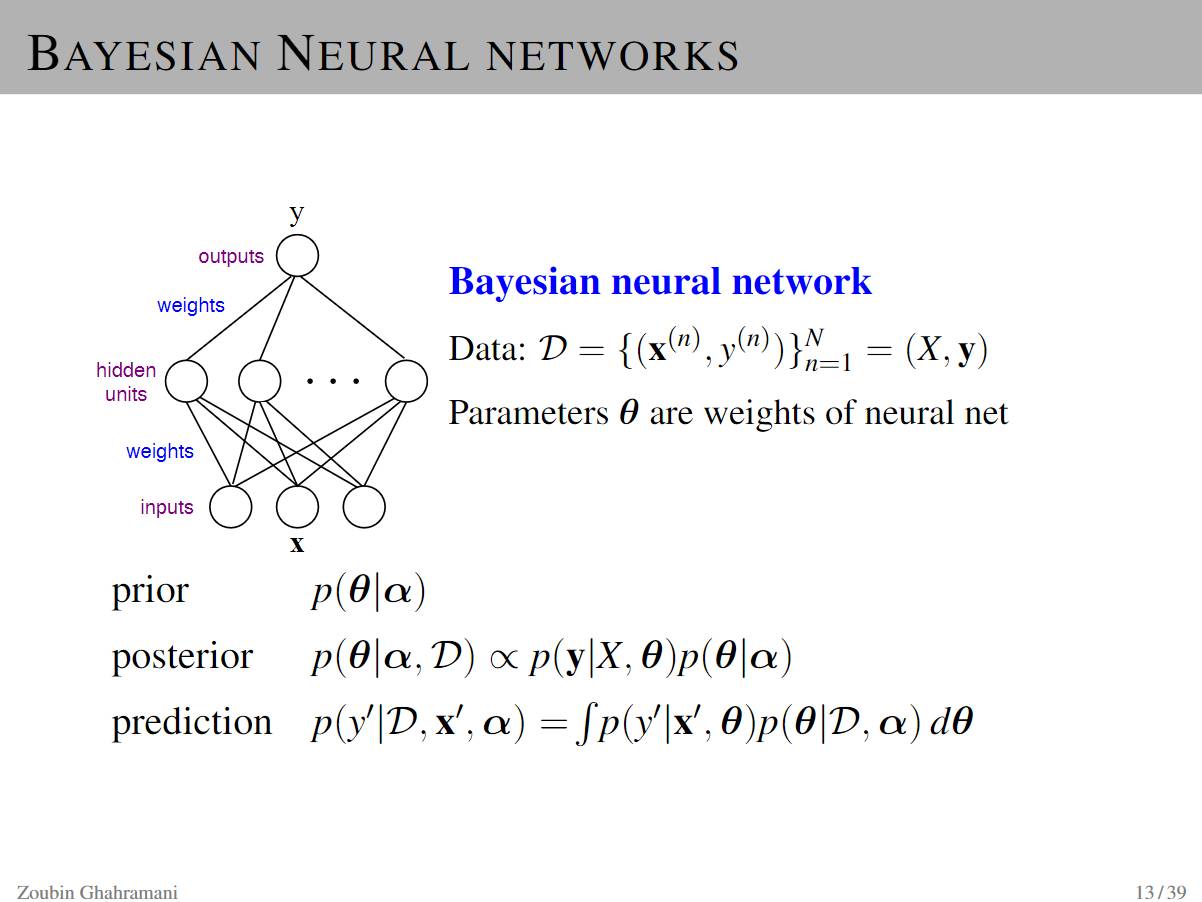
P13: Bayesian Neural Networks

P14-16: Early History of Bayesian Neural Networks

The early history of Bayesian neural networks can be understood from the following papers:

• John Denker, Daniel Schwartz, Ben Wittner, Sara Solla, Richard Howard, Lawrence Jackel, and John Hopfield. Large automatic learning, rule extraction, and generalization. Complex Systems, 1(5):877-922, 1987.

• Nafitali Tishby, Esther Levin, and Sara A Solla. Consistent inference of probabilities in layered networks: Prediction and generalization. In IJCNN, 1989.

• ……

P17-20: The Golden Age of Bayesian Neural Networks

• David JC Mackay published an article in Neural Computation: A Practical Bayesian Framework For Backpropagation Networks, marking the beginning of this period.

• Neal, R.M. 1995 PhD thesis at the University of Toronto: Bayesian learning for neural networks. This thesis also established the relationship between Bayesian neural networks (BNN) and Gaussian processes as well as automatic relevance determination (ARD).

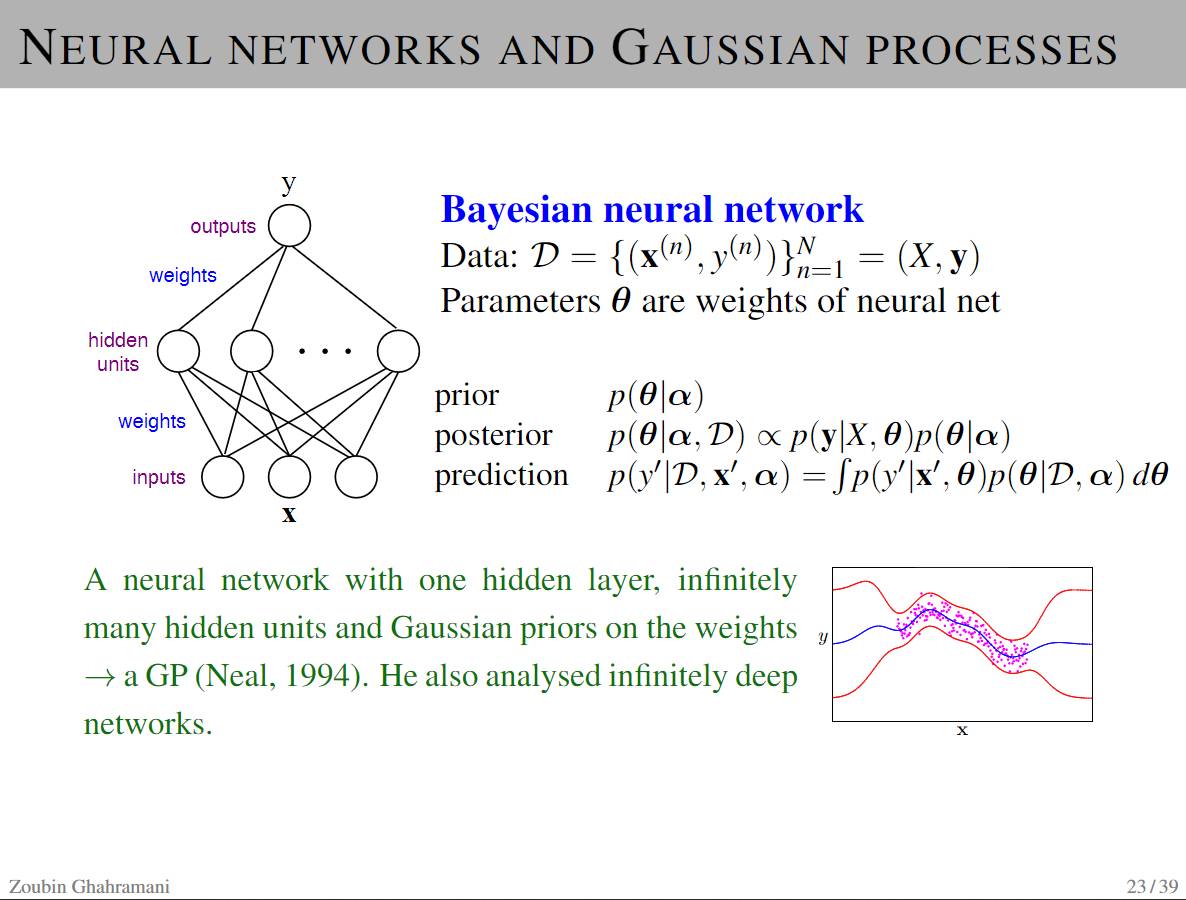
P21-24: Gaussian Processes and Bayesian Neural Networks

• Gaussian processes can be used for regression, classification, ranking, etc.

• Combining Langevin dynamics (a form of MCMC) with stochastic gradient descent (SGD) yields a highly scalable approximate MCMC algorithm based on minibatch SGD.

• This way, Bayesian inference can be as simple as running noisy SGD.

• A neural network with one hidden layer and numerous hidden units and weight Gaussian priors

• MacKay and Neal’s contributions linked feature and architecture selection with Gaussian processes.

P25-28: Variational Learning in Bayesian Neural Networks

• A paper by Hinton derives a diagonal Gaussian variational approximation for Bayesian network weights, described in the language of minimum description length information theory.

P29: Stochastic Gradient Langevin Dynamics

P30: The Revival of Bayesian Neural Networks

P31-32: When Do Probabilistic Methods Become Very Important?

• Many aspects of learning rely heavily on detailed representations of uncertainty.

P33: Conclusion

Probabilistic models provide a general framework for establishing systems that can learn from data.

Bayesian neural networks have a long history and are experiencing a wave of revival.

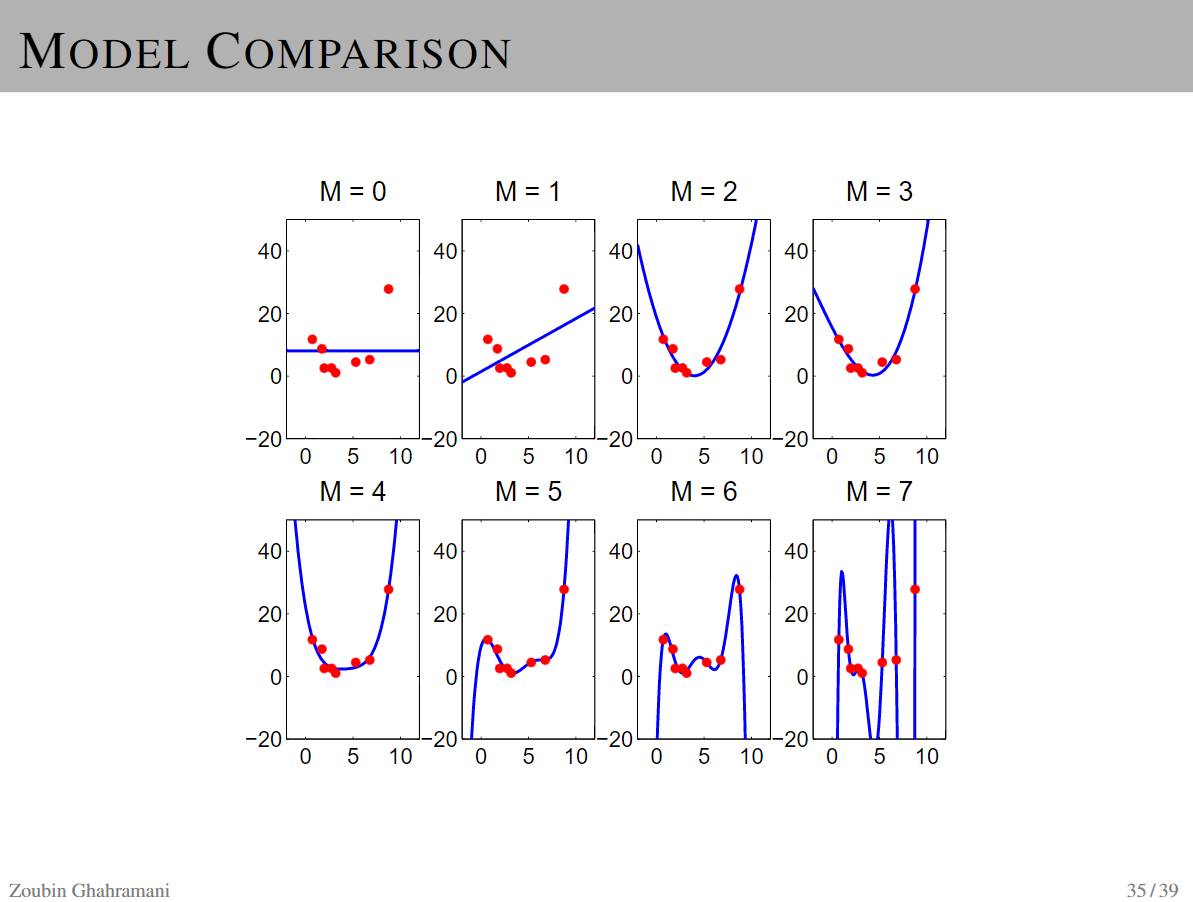
P35-36: Model Comparison and Learning Model Structures

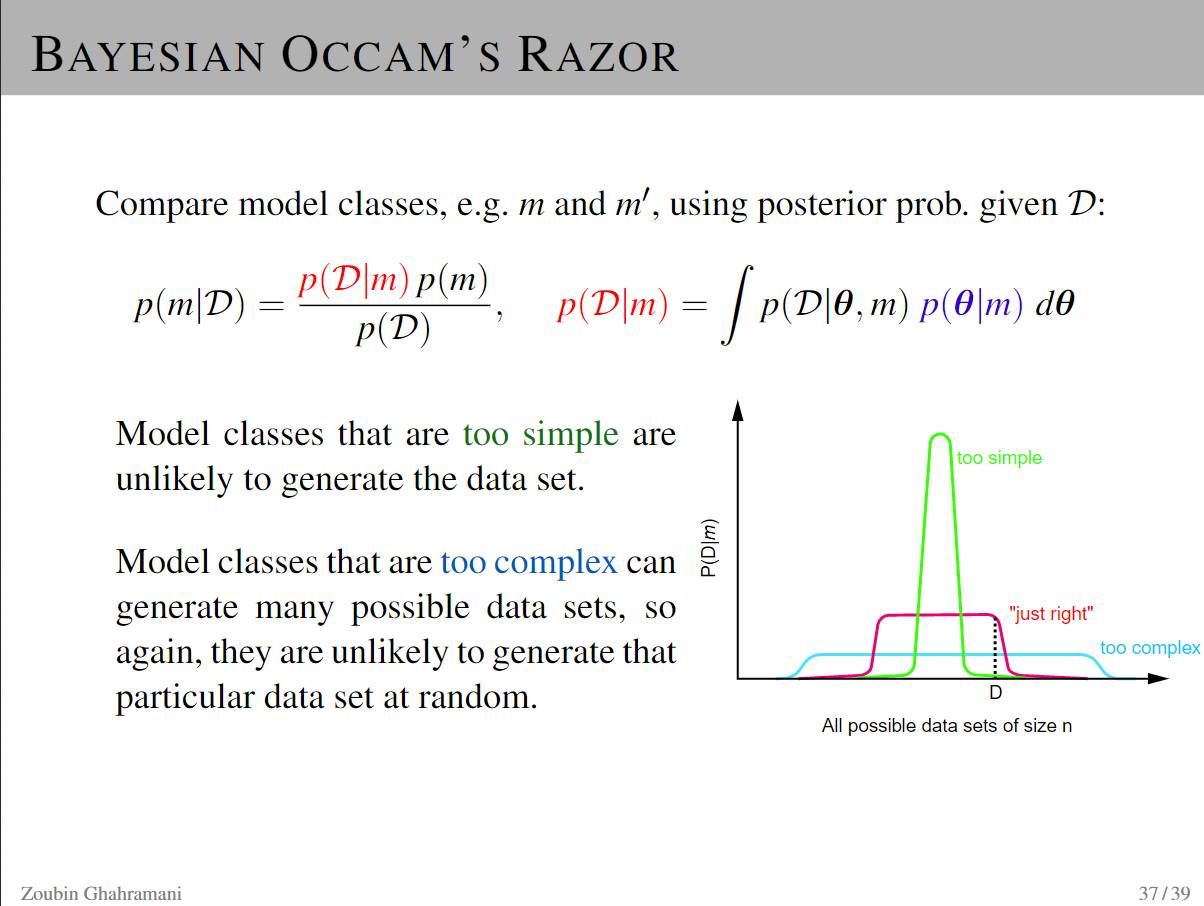
P37-39: Bayesian Occam’s Razor

• Model classes that are too simple may not generate datasets.

• Complex model classes can generate many possible datasets, so they are also less likely to randomly generate a specific dataset.

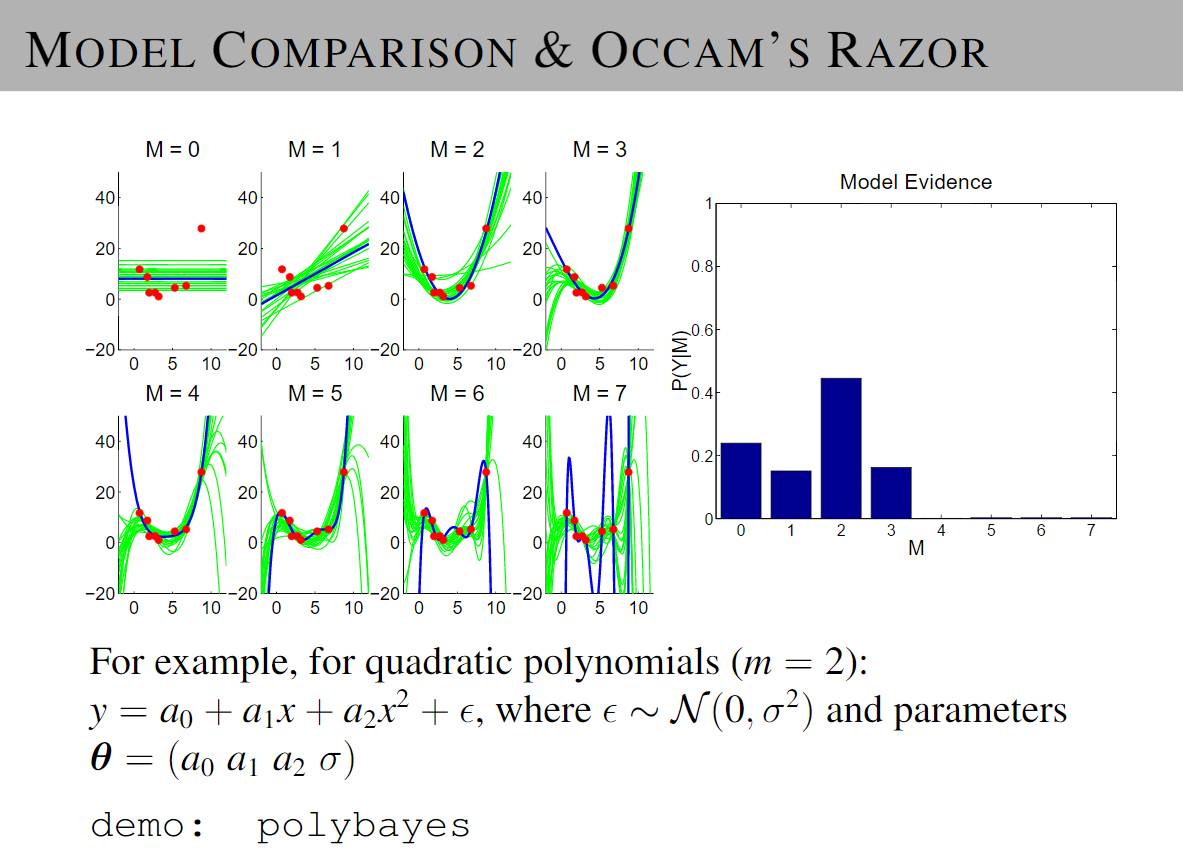
P40: Model Comparison and Occam’s Razor

P41-42: Approximation Methods for Marginal Likelihood and Posteriors

• Laplace Approximation

• Bayesian Information Criterion (BIC)

• Variational approximations

• Expectation Propagation (EP)

• Markov Chain Monte Carlo methods (MCMC)

• Sequential Monte Carlo (SMC)

• Exact Sampling

• ……

Click to read the original text for the complete PPT

This article is compiled by Machine Heart, please contact this public account for authorization to reprint.

✄————————————————

Join Machine Heart (Full-time Journalist/Intern): [email protected]

Submissions or seeking coverage: [email protected]

Advertising & Business Cooperation: [email protected]