Visualizing the Structure of LSTM Models

Source: Deep Learning Enthusiasts


This article is about 3300 words, and it is recommended to read for more than 10 minutes.
This article uses a visual presentation to help you deeply understand the structure of LSTM models.

I have recently been learning about the application of LSTM in time series prediction, but I encountered a significant problem: after adding time steps to the traditional BP network, its structure becomes very difficult to understand, and the input-output data format is also hard to grasp. There are many articles online that introduce the structure of LSTM, but they are not intuitive and are very unfriendly to beginners. I struggled for a long time, looking at a lot of materials and shared LSTM structure diagrams from netizens before I understood the intricacies.The content of this article is as follows:

1. Traditional BP Networks and CNN Networks
2. LSTM Networks
3. LSTM Input Structure
4. LSTM in PyTorch
   4.1 LSTM Model Defined in PyTorch
   4.2 Data Format for Feeding into LSTM
   4.3 Output Format of LSTM
5. LSTM Combined with Other Networks

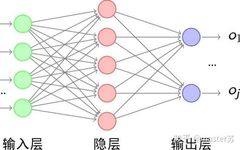
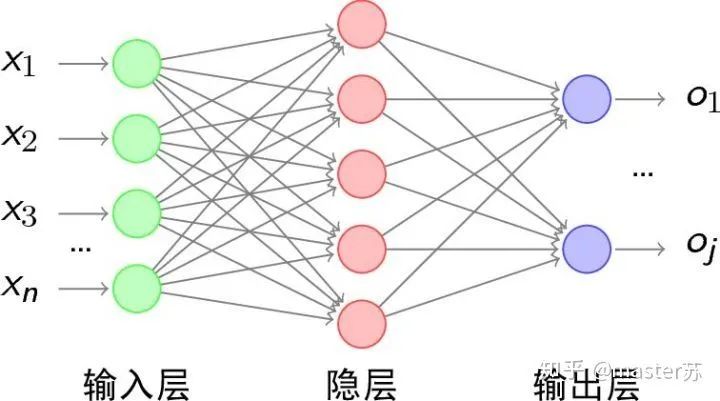
1. Traditional BP Networks and CNN NetworksBP networks and CNN networks do not have a time dimension, and they are similar to traditional machine learning algorithms. CNN can be understood as stacking multiple layers when processing color images with three channels, treating the three-dimensional matrix of the image as spatial slices. When writing code, one can simply follow the diagram layer by layer. The following images show a typical BP network and CNN network.

BP Network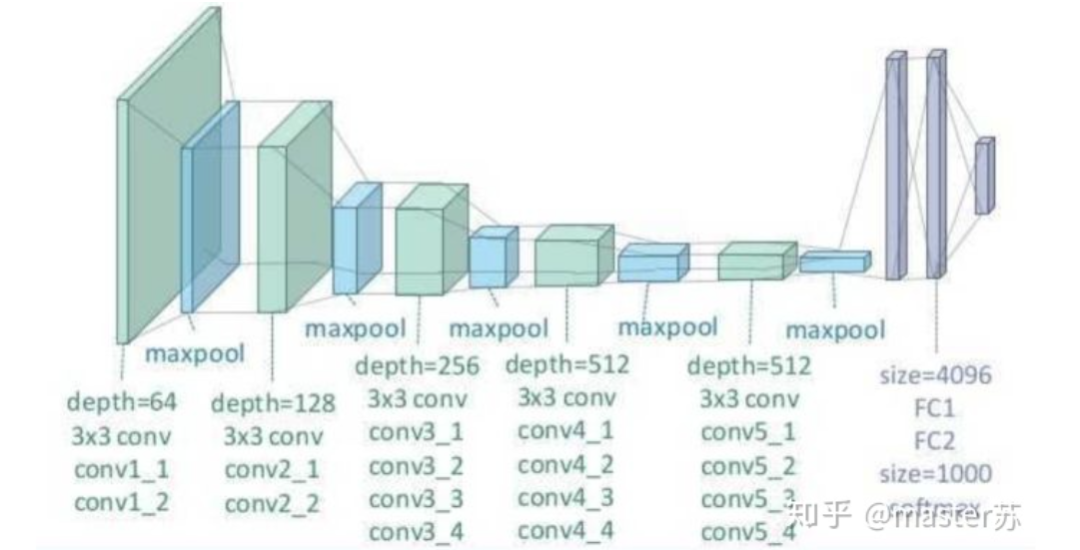

CNN NetworkThe hidden layers, convolutional layers, pooling layers, and fully connected layers in the diagram are all practically existing, stacked layer by layer, making it easy to understand spatially. Therefore, when writing code, one basically just follows the diagram. For example, using Keras:

# Sample code, no practical significance
model = Sequential()
model.add(Conv2D(32, (3, 3), activation='relu'))  # Add convolutional layer
model.add(MaxPooling2D(pool_size=(2, 2)))         # Add pooling layer
model.add(Dropout(0.25))                          # Add dropout layer
model.add(Conv2D(32, (3, 3), activation='relu'))  # Add convolutional layer
model.add(MaxPooling2D(pool_size=(2, 2)))         # Add pooling layer
model.add(Dropout(0.25))                          # Add dropout layer
....   # Add other convolution operations
model.add(Flatten())                            # Flatten three-dimensional array to two-dimensional array
model.add(Dense(256, activation='relu'))        # Add ordinary fully connected layer
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax'))
....  # Train the network

2. LSTM NetworksWhen we search for LSTM structures online, the most common image we see is the one below: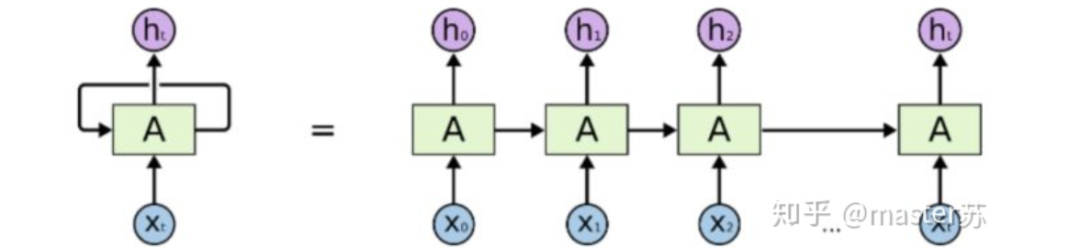RNN NetworkThis is the classic structure diagram of the RNN (Recurrent Neural Network). LSTM simply improves the nodes A in the hidden layer while keeping the overall structure unchanged. Therefore, this article also discusses the visualization of this structure.The middle node A in the hidden layer represents an LSTM network with only one hidden layer on the left, while the so-called LSTM recurrent neural network utilizes the time axis for cyclic reuse. When expanded along the time axis, we obtain the right diagram.Looking at the left diagram, many students mistakenly believe that LSTM is a network structure with single input and single output, having only one hidden neuron. Looking at the right diagram, they think LSTM is a network structure with multiple inputs and outputs, having multiple hidden neurons. The number of A represents the number of hidden layer nodes.WTH? It’s hard to wrap my mind around this. This is the traditional network and spatial structure thinking.In reality, in the right diagram, we see Xt representing the sequence, where the subscript t is the time axis. Therefore, the number of A represents the length of the time axis, indicating the state (Ht) of the same neuron at different times, not the number of hidden layer neurons.We know that LSTM networks use information from the previous moment, combined with the input information from the current moment, to train together.For example, on the first day I got sick (initial state H0), then took medicine (using input information X1 to train the network), the next day I felt better but was not completely well (H1), took medicine again (X2), and my condition improved (H2). This cycle continues until I recover. Thus, the input Xt is taking medicine, the time axis T represents the number of days taking medicine, and the hidden layer state represents my health condition. Therefore, I remain the same person, just in different states.In fact, the structure of the LSTM network is as follows:

LSTM Network Structure

The above diagram represents an LSTM network with 2 hidden layers. At time T=1, it appears as a normal BP network, and at T=2, it also appears as a normal BP network. However, when expanded along the time axis, the hidden layer information H and C trained at T=1 will be passed to the next moment T=2, as shown in the diagram below. The five arrows pointing right in the above diagram also indicate the transmission of hidden layer states along the time axis.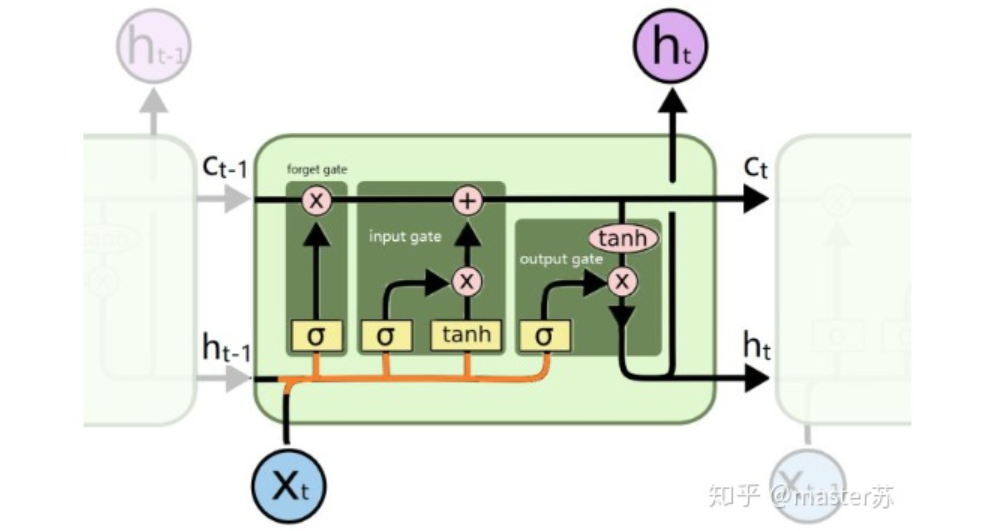Note that in the diagram, H represents the hidden layer state, and C is the forget gate, which will be explained later regarding their dimensions.3. LSTM Input StructureTo better understand the LSTM structure, it is also necessary to comprehend the input data situation for LSTM. Mimicking the appearance of a three-channel image, the data cube of multi-samples with multiple features at different moments along the time axis is shown in the diagram below:

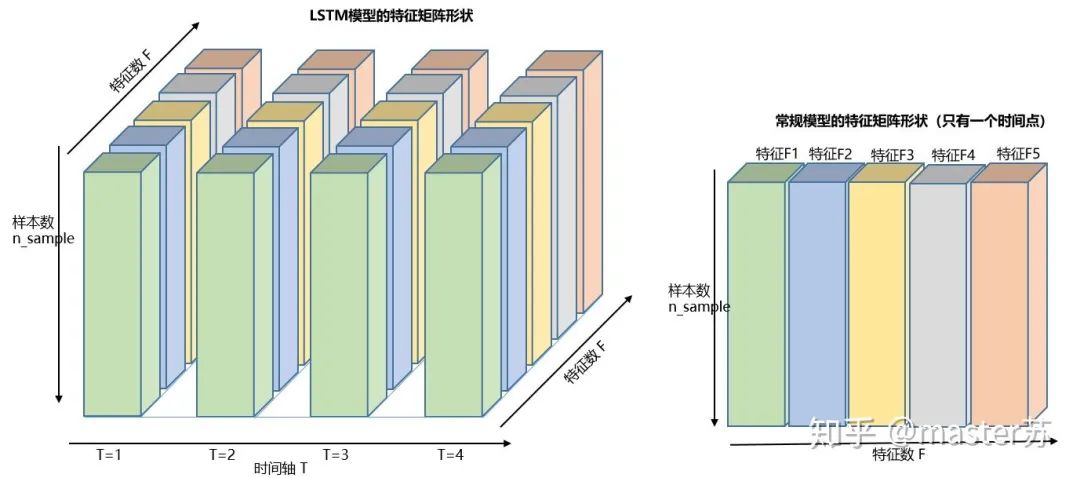Three-dimensional Data Cube

The diagram on the right shows the input format of common models, such as XGBOOST, lightGBM, decision trees, etc., where the input data format is a (N*F) matrix. The left diagram shows the data cube with the time axis added, which is a slice along the time axis. Its dimensions are (N*T*F), where the first dimension is the number of samples, the second dimension is time, and the third dimension is the number of features, as shown in the diagram below:

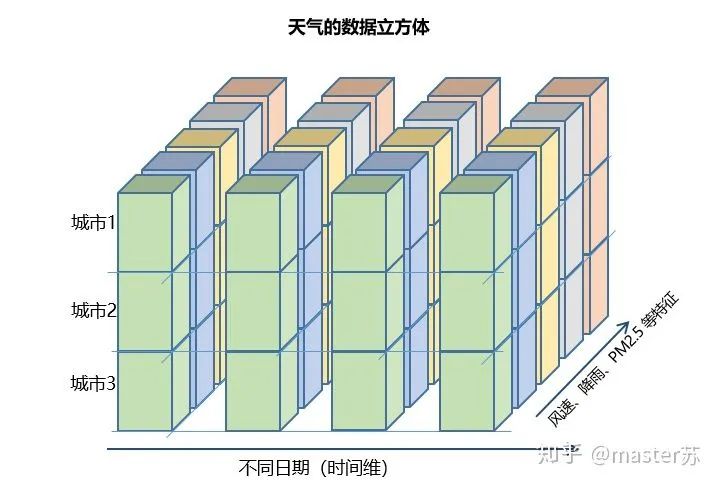
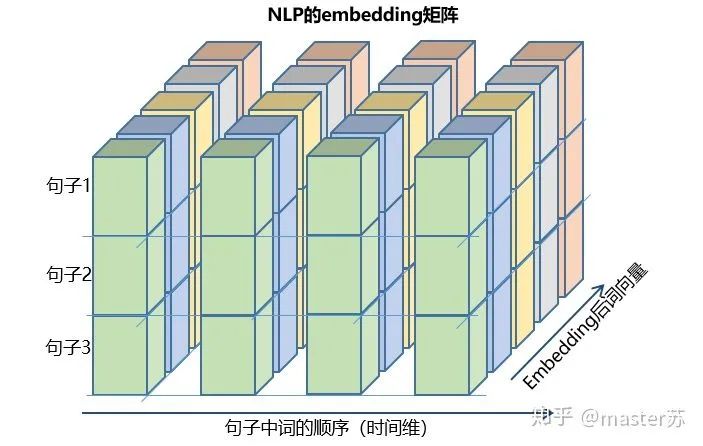
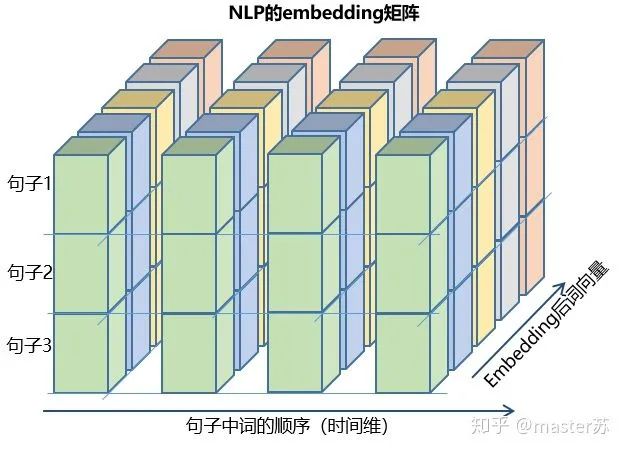
This type of data cube is common, for example in weather forecast data, where samples can be understood as cities, the time axis represents dates, and features include weather-related data such as rainfall, wind speed, PM2.5, etc. This data cube is easy to understand. In NLP, a sentence is embedded into a matrix, where the order of words corresponds to the time axis T. The embedding of multiple sentences forms a three-dimensional matrix as shown in the diagram below:

4. LSTM in PyTorch

4.1 LSTM Model Defined in PyTorch

The parameters of the LSTM model defined in PyTorch are as follows:

class torch.nn.LSTM(*args, **kwargs)
Parameters include:
    input_size: Feature dimension of x
    hidden_size: Feature dimension of the hidden layer
    num_layers: Number of LSTM hidden layers, default is 1
    bias: If False, bihbih=0 and bhhbhh=0. Default is True
    batch_first: If True, the input-output data format is (batch, seq, feature)
    dropout: Dropout is applied to the output of each layer except the last one, default is: 0
    bidirectional: If True, it is a bidirectional LSTM, default is False

Combining with the previous diagrams, let’s examine each parameter.(1) input_size:The feature dimension of x, which corresponds to F in the data cube. In NLP, this is the length of the vector after embedding a word, as shown in the diagram below: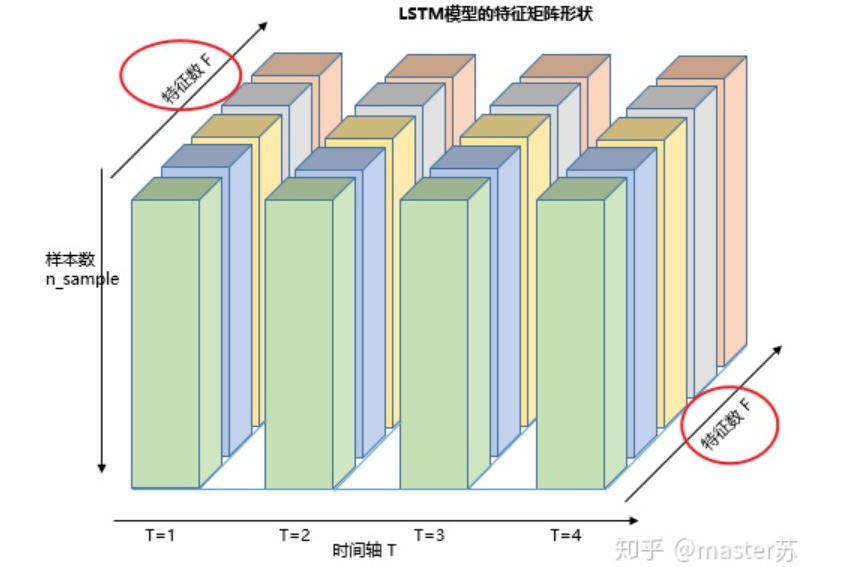(2) hidden_size:The feature dimension of the hidden layer (number of hidden layer neurons), as shown in the diagram below. We have two hidden layers, each with a feature dimension of 5. Note that the output dimension of a non-bidirectional LSTM equals the hidden layer feature dimension.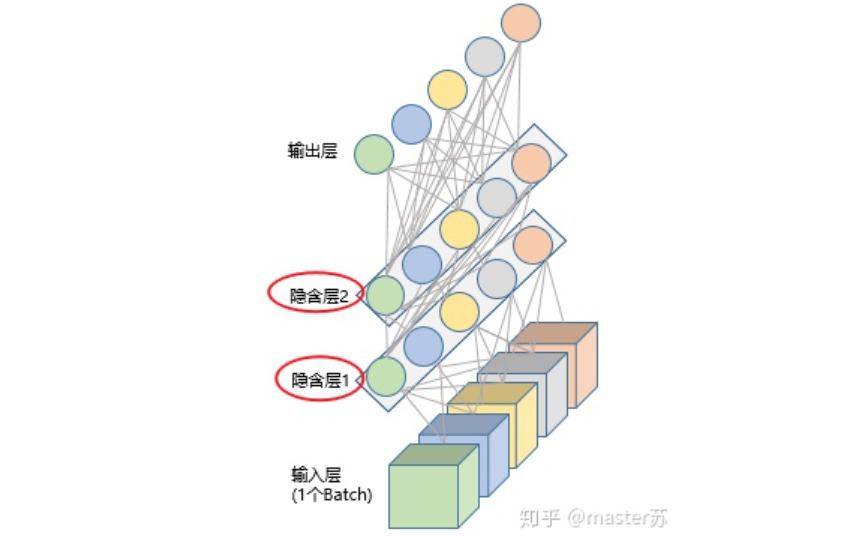(3) num_layers:The number of LSTM hidden layers, as defined in the above diagram, we have 2 hidden layers.(4) batch_first:This defines the input-output dimensions, which will be discussed later.(5) bidirectional:Whether it is a bidirectional recurrent neural network. The diagram below shows a bidirectional recurrent neural network. Therefore, when using a bidirectional LSTM, I need to pay special attention: during forward propagation, there are (Ht, Ct), and during backward propagation, there are also (Ht’, Ct’). As mentioned earlier, the output dimension of a non-bidirectional LSTM equals the hidden layer feature dimension, while the output dimension of a bidirectional LSTM is the number of hidden layer features * 2, and the dimensions of H and C are the length of the time axis * 2.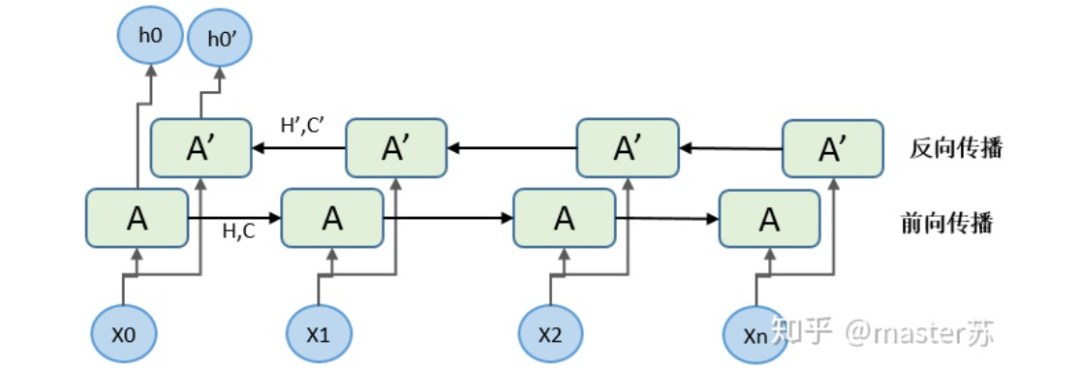

4.2 Data Format for Feeding into LSTM

The default input data format for LSTM in PyTorch is as follows:

input(seq_len, batch, input_size)
Parameters include:
    seq_len: Sequence length, which is the sentence length in NLP, usually padded with pad_sequence to equalize lengths
    batch: The number of data entries fed into the network at once, which is the number of sentences fed into the network at one time in NLP
    input_size: Feature dimension, consistent with the input_size defined in the network structure earlier.

It was previously mentioned that if the LSTM parameter batch_first=True, then the required input format is:

input(batch, seq_len, input_size)

Just swapping the first two parameters. This is a relatively easy-to-understand data format. Below, we will explain how to construct the LSTM input using embedding vectors in NLP.Previously, our embedding matrix was as shown in the diagram below:

If we place the batch first, the three-dimensional matrix format is as follows:

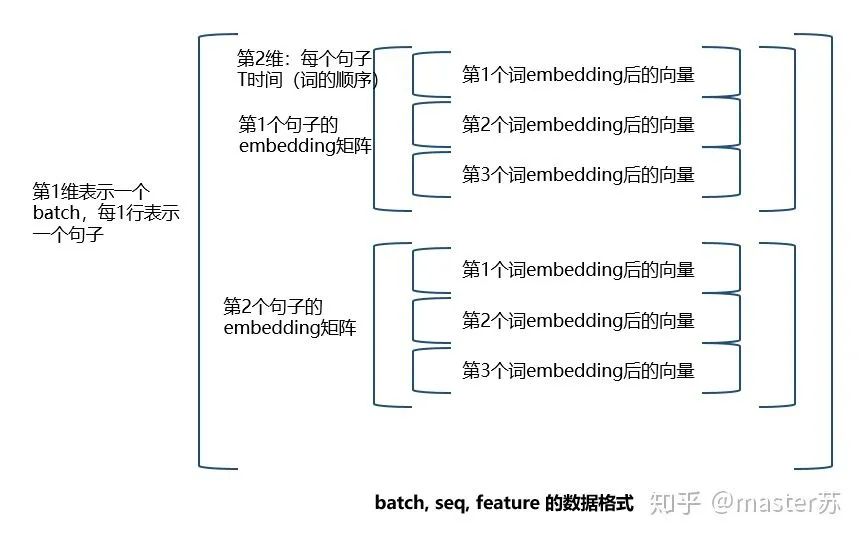
The conversion process is shown in the diagram below:

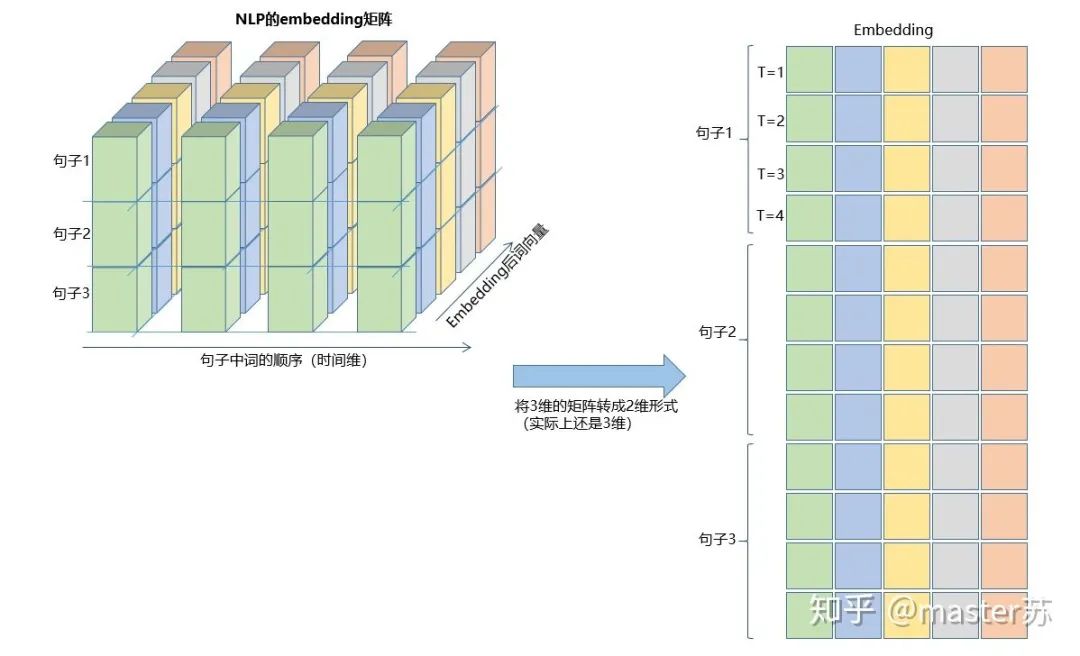
Did you understand? This is the format of the input data, isn’t it simple?The other two inputs for LSTM are h0 and c0, which can be understood as the network’s initialization parameters, generated using random numbers.

h0(num_layers * num_directions, batch, hidden_size)
c0(num_layers * num_directions, batch, hidden_size)
Parameters:
    num_layers: Number of hidden layers
    num_directions: If it is a unidirectional recurrent network, then num_directions=1; if bidirectional, then num_directions=2
    batch: Input data batch
    hidden_size: Number of hidden layer neurons

Note that if we define the input format as:

input(batch, seq_len, input_size)

Then the formats for H and C must also change:

h0(batch, num_layers * num_directions, h, hidden_size)
c0(batch, num_layers * num_directions, h, hidden_size)

4.3 Output Format of LSTM

The output of LSTM is a tuple as follows:

output,(ht, ct) = net(input)
    output: Output of the last state of the hidden layer neurons
    ht: State value of the last state of the hidden layer
    ct: Forget gate value of the last state of the hidden layer

The default dimensions of output are:

output(seq_len, batch, hidden_size * num_directions)
ht(num_layers * num_directions, batch, hidden_size)
ct(num_layers * num_directions, batch, hidden_size)

Similar to the input situation, if we previously defined the input format as:

input(batch, seq_len, input_size)

Then the formats for ht and ct must also change:

ht(batch, num_layers * num_directions, h, hidden_size)
ct(batch, num_layers * num_directions, h, hidden_size)

After all this, let’s go back and see where ht and ct are. Please refer to the diagram below: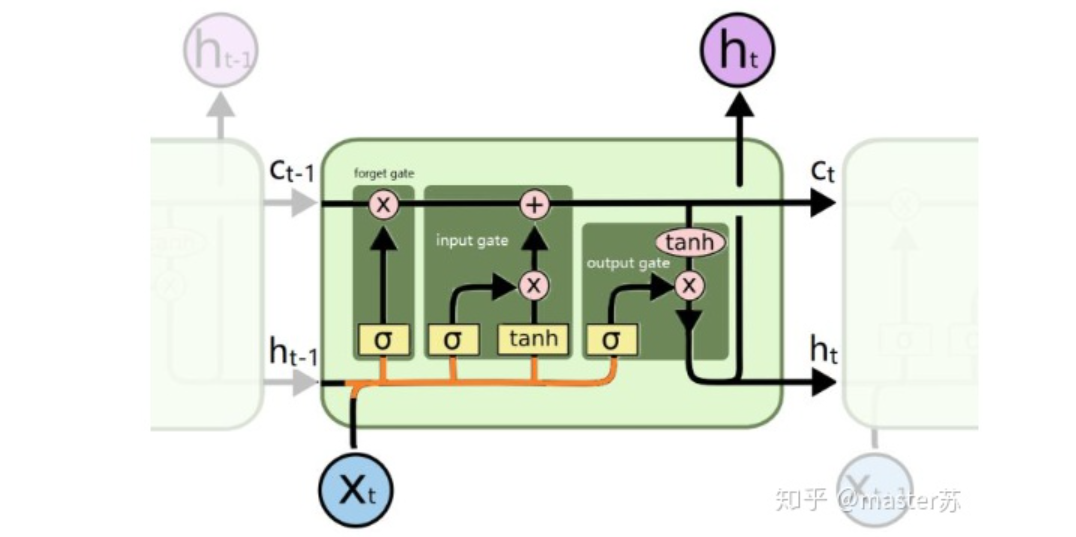Where is the output? Please refer to the diagram below: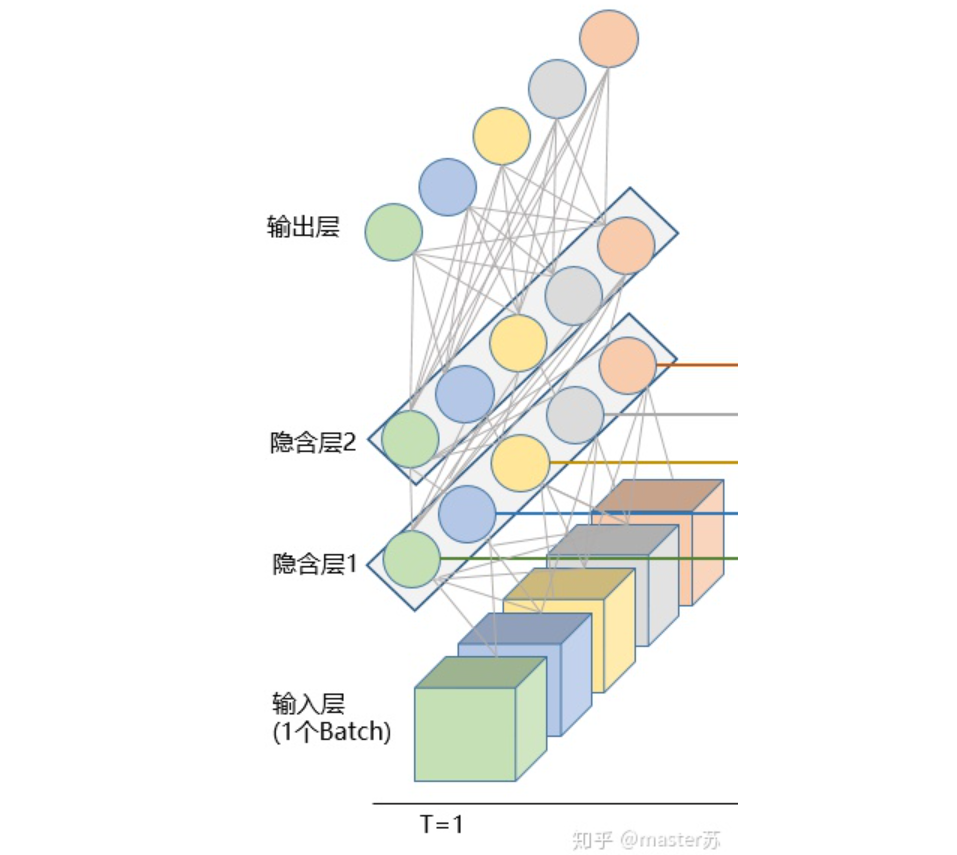5. LSTM Combined with Other NetworksDo you remember? The dimension of the output equals the number of hidden layer neurons, which is hidden_size. In some time series predictions, a fully connected layer is often added after the output, where the input dimension of the fully connected layer equals the LSTM’s hidden_size. After that, the processing of the network is the same as that of the BP network, as shown in the diagram below:

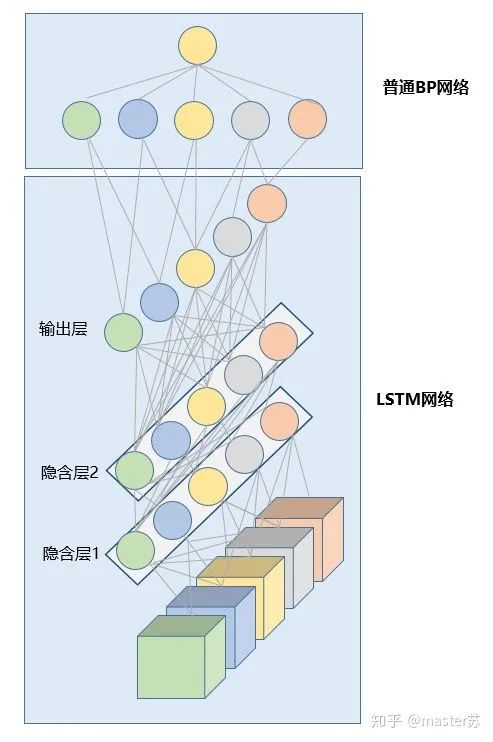
Implementing the above structure in PyTorch:

import torch
from torch import nn
class RegLSTM(nn.Module):
    def __init__(self):
        super(RegLSTM, self).__init__()
        # Define LSTM
        self.rnn = nn.LSTM(input_size, hidden_size, hidden_num_layers)
        # Define regression layer network, input feature dimension equals LSTM output, output dimension is 1
        self.reg = nn.Sequential(
            nn.Linear(hidden_size, 1)
        )
    def forward(self, x):
        x, (ht,ct) = self.rnn(x)
        seq_len, batch_size, hidden_size= x.shape
        x = y.view(-1, hidden_size)
        x = self.reg(x)
        x = x.view(seq_len, batch_size, -1)
        return x

Of course, some models use the output as the input to another LSTM, or use the information from the hidden layers ht and ct for modeling, and so on.Well, that’s all about my learning insights on LSTM. After reading, remember to follow and like.Reference links:https://zhuanlan.zhihu.com/p/94757947https://zhuanlan.zhihu.com/p/59862381https://zhuanlan.zhihu.com/p/36455374https://www.zhihu.com/question/41949741/answer/318771336https://blog.csdn.net/android_ruben/article/details/80206792Links:https://zhuanlan.zhihu.com/p/139617364This article is for academic exchange only. If there is any infringement, please contact the backend for deletion.

Editor: Huang Jiyan

Proofreader: Lin Yilin