0Introduction
Nowadays, discussions about machine learning, deep learning, and artificial neural networks are becoming more prevalent. However, programmers often just want to use these magical frameworks without wanting to understand how they actually work. But if we can grasp the principles behind them, wouldn’t it be better for their usage? Today, we will discuss recurrent neural networks and the fundamental mathematical principles behind them that enable RNNs to perform tasks that other neural networks cannot.

The purpose of this article is to provide an intuitive understanding of the functions and structure of recurrent neural networks.
A neural network typically takes independent variables (or a set of independent variables) and dependent variables, then learns the mapping between (which we call training). Once training is complete, it can predict the corresponding dependent variable when given a new independent variable.
But what if the order of the data is important? Imagine if the order of all independent variables is crucial?
Let me explain intuitively.

Assuming each ant is an independent variable, if one ant moves in a different direction, it doesn’t matter to the other ants, right? But what if the order of the ants is important?

In this case, if one ant misses or leaves the group, it will affect the ants that follow.
So, in the space of machine learning, which data sequences are important?
- Natural language data’s word order issues
- Speech data
- Time series data
- Video/music sequence data
- Stock market data
- And so on
So how does RNN handle data where overall order is important? Let’s use natural text data as an example to explain RNN.
Assume I am performing sentiment analysis on user reviews of a movie.
From 这部电影好 (This movie is good) — positive, to 这部电影差 (This movie is bad) — negative.
We can classify them using a simple bag-of-words model, and we can predict (positive or negative), but wait.
What if the review is 这部电影不好 (This movie is not good)?
The BOW model might say this is a positive signal, but it is not. RNN understands this and predicts it as negative information.
1How Does RNN Achieve This?
1Types of RNN Models
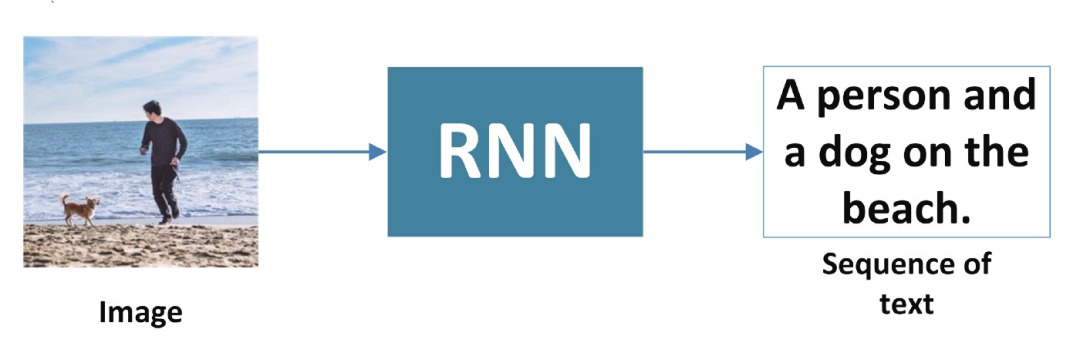
1. One-to-Many
RNN takes an input, such as an image, and generates a sequence of words.
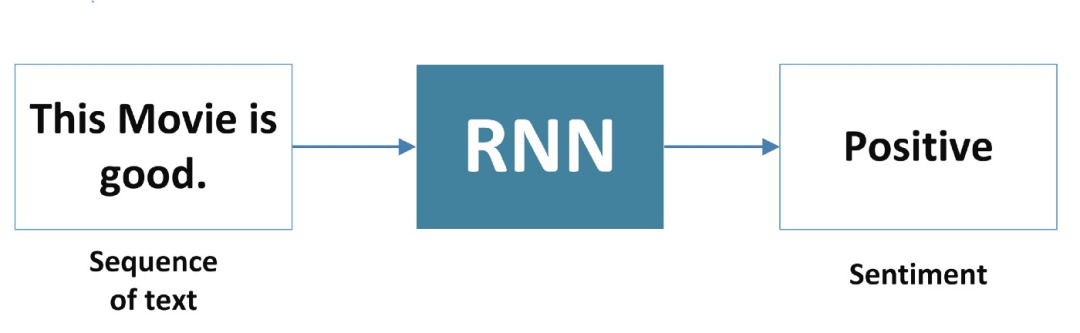
2. Many-to-One
RNN takes a sequence of words as input and generates an output.
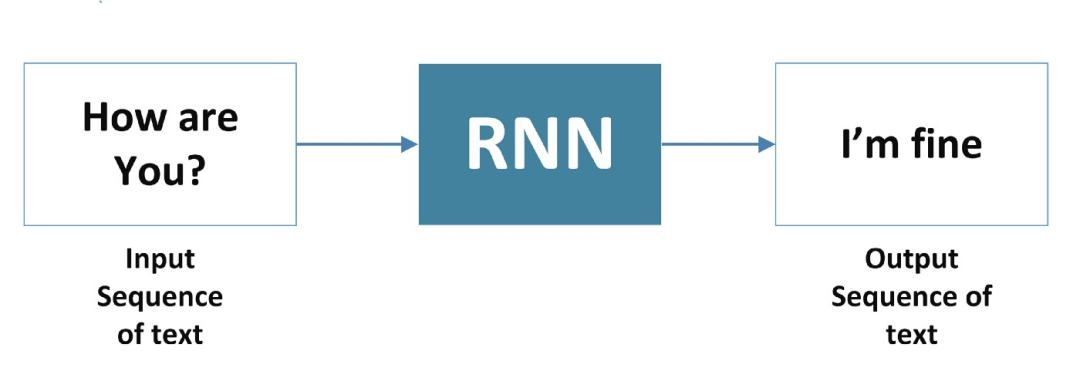
3. Many-to-Many
Next, we are focusing on the second mode Many-to-One. The input of RNN is considered as time steps.
Example: Input(X) = [” this “, ” movie “, ” is “, ” good “]
The timestamp of this is x(0), movie is x(1), is is x(2), good is x(3).
2Network Architecture and Mathematical Formulas
Now let’s delve into the mathematical world of RNNs.
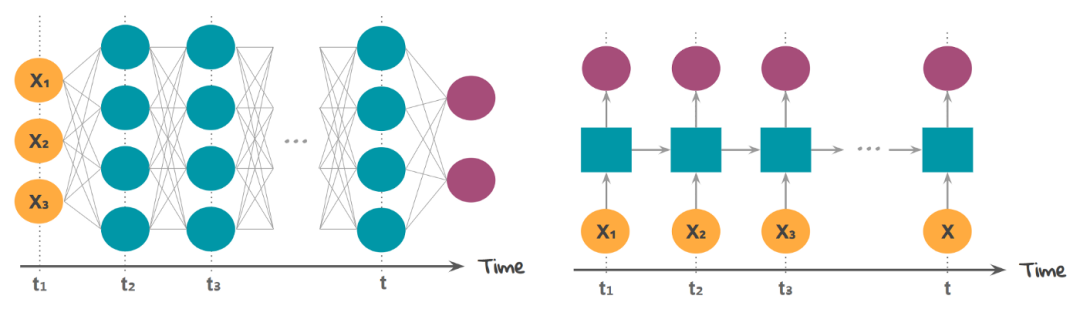
First, let’s understand what an RNN cell contains! I hope and assume everyone knows about feedforward neural networks, the overview of FFNN.
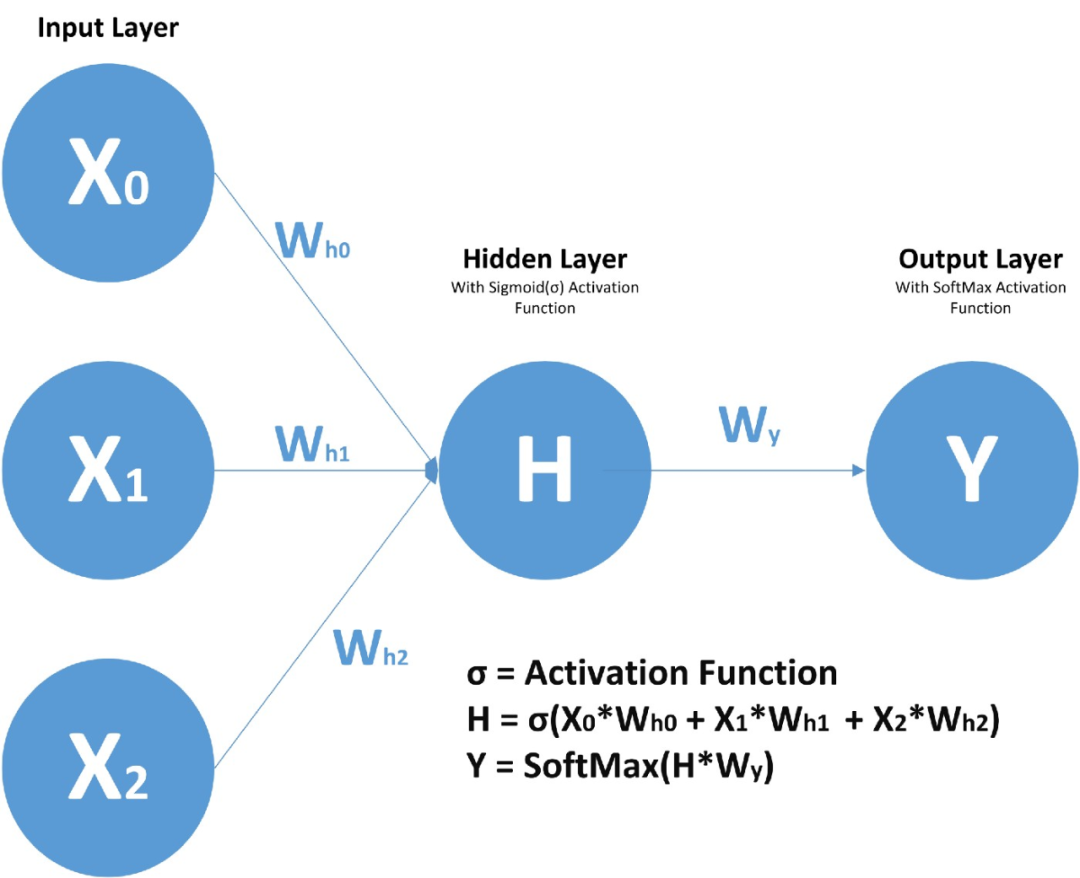

In a feedforward neural network, we have X(input), H(hidden), and Y(output). We can have any number of hidden layers, but the weights W for each hidden layer and the input weights corresponding to each neuron are different.
Above, we have weights Wy10 and Wy11, corresponding to the weights of two different layers relative to output Y, while Wh00, Wh01, etc., represent different weights for neurons relative to input.
Due to the presence of time steps, the neural network unit contains a set of feedforward neural networks. This neural network has characteristics of sequential input, sequential output, multiple time steps, and multiple hidden layers.
Unlike FFNN, here we not only calculate the hidden layer values from the input values, but also from the values of previous time steps. For the time steps, the hidden layer weights (W) are the same. Below is a complete image of the RNN and the mathematical formulas involved.
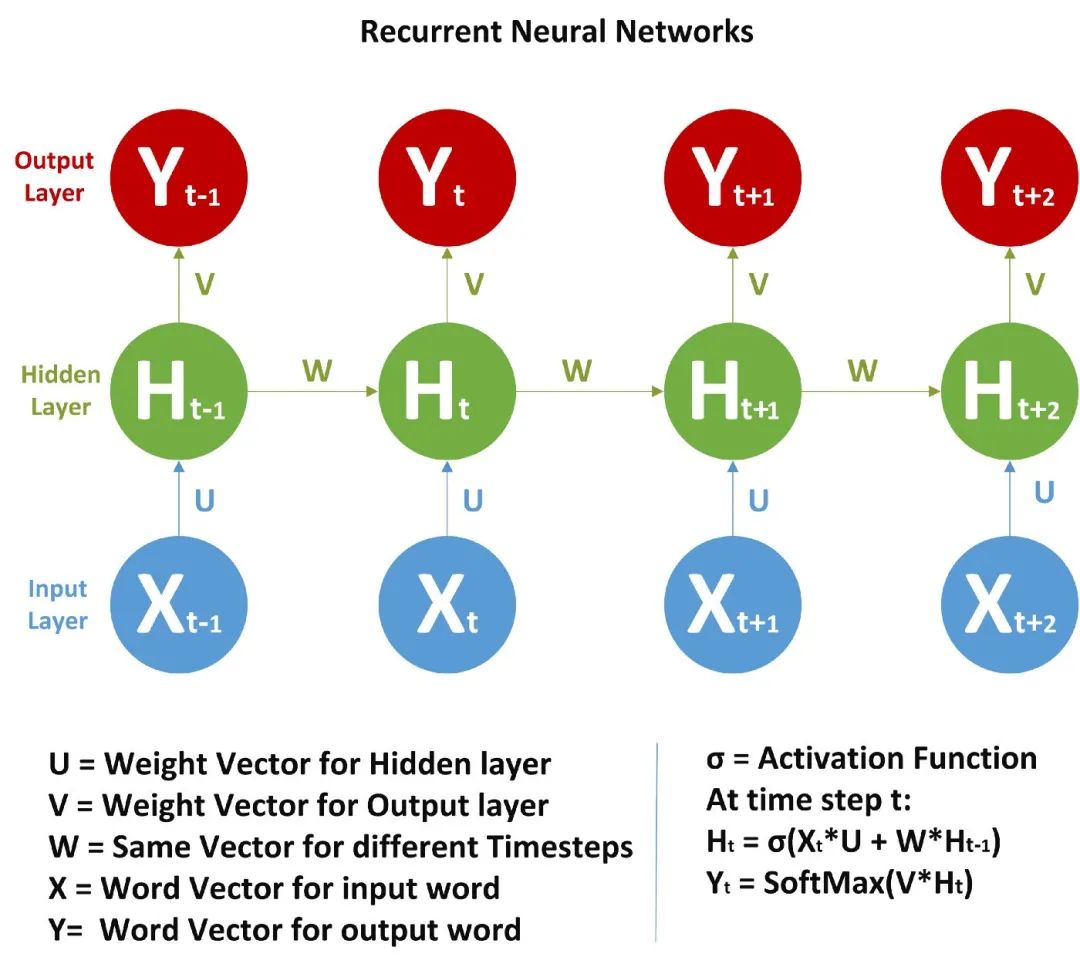
In the image, we are calculating the value of the hidden layer at time step t:
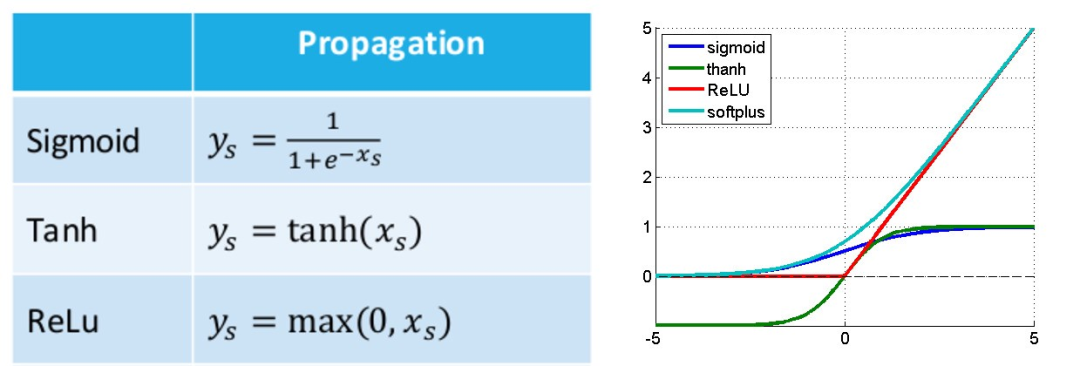
- is the previous time step. I mentioned that W is the same for all time steps. Activation functions can be Tanh, Relu, Sigmoid, etc.
Above we only calculated Ht, similarly, we can calculate all other time steps.
Steps:
-
1. Calculate from and
-
2. Calculate from and
-
3. Calculate from and and
-
4. Calculate from and , and so forth.
Note:
-
1. and are weight vectors, different for each time step.
-
2. We can even calculate the hidden layer(all time steps) first, then calculate the values.
-
3. The weight vectors are random at the beginning.
Once the feedforward input is complete, we need to calculate the error and use backpropagation to propagate the error backward, using cross-entropy as the cost function.
2BPTT (Backpropagation Through Time)
If you know how a regular neural network works, the rest is simple. If you are unclear, you can refer to previous articles on artificial neural networks in this account.
We need to calculate the following:
- 1. How does the total error change with respect to the output(hidden and output units)?
- 2. How does the output change concerning the weights(U, V, W)?
Since W is the same for all time steps, we need to go back to update.
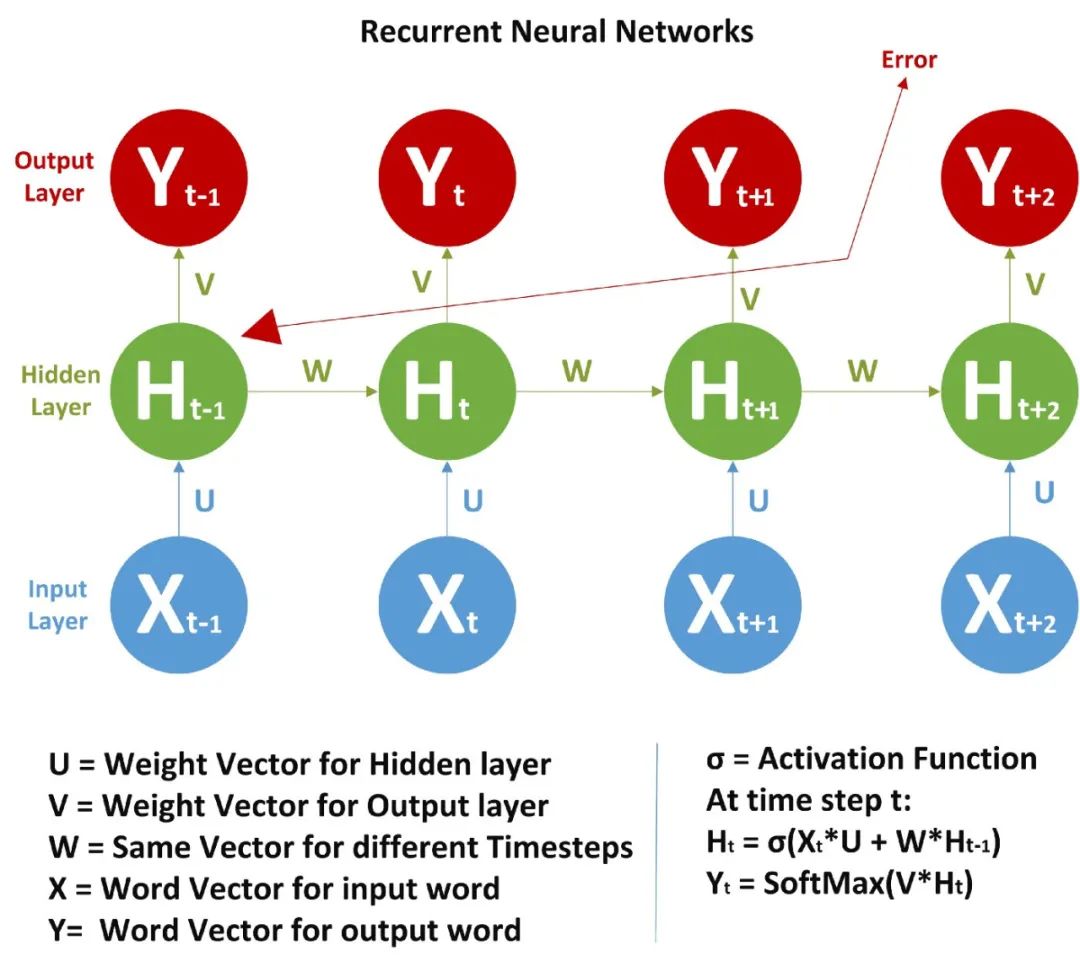
Remember that the backpropagation in RNN is the same as in artificial neural networks, but here the current time step is calculated based on the previous time steps, so we must traverse back and forth from start to end.
If we apply the chain rule, like this
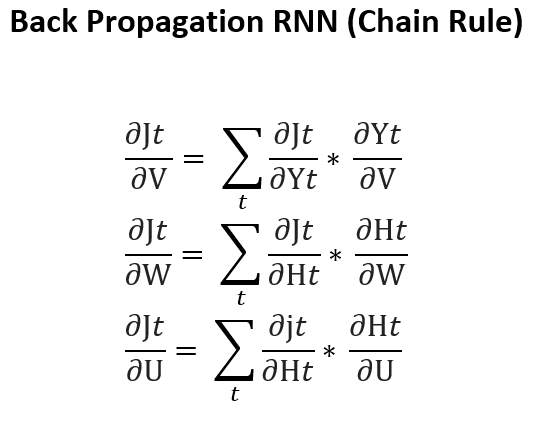
Since W is the same across all time steps, the terms expand more and more according to the chain rule.
In Richard Socher’s lecture slides on recurrent neural networks[1], you can see a similar but different method of calculating formulas.
- A similar but more concise RNN formula:
- The total error is the sum of errors at each time step t:
- Application of the chain rule:
So here, is the same as our .
、、 can be updated using any optimization algorithm, such as gradient descent.
2Back to the Example
Now let’s return to our sentiment analysis problem, here is an RNN,
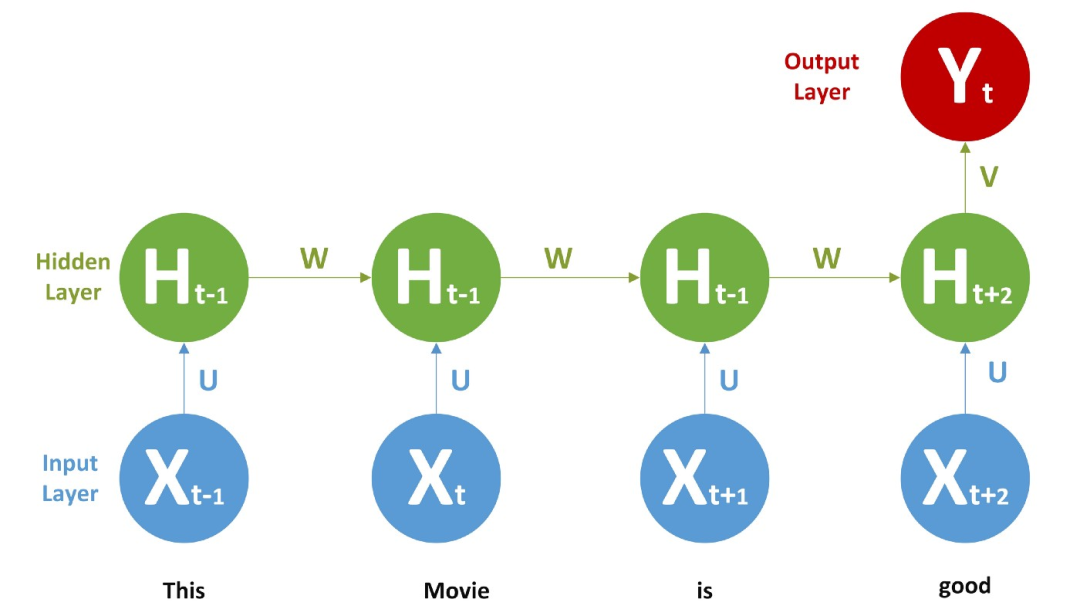
We provide each word with a word vector or a one-hot encoding vector as input, and perform feedforward and BPTT. Once training is complete, we can input new text for prediction. It will learn something like not + positive word = negative.
RNN’s problem → Vanishing/Exploding Gradient Problem
Since W is the same for all time steps, during backpropagation, when we go back to adjust the weights, the signals can become either too weak or too strong, leading to either vanishing or exploding problems. To avoid this, we use GRU or LSTM, which will be introduced in subsequent articles.
⟳References⟲
[1]
Richard Socher’s lecture slides on recurrent neural networks: http://cs224d.stanford.edu/lectures/CS224d-Lecture7.pdf
[2]
English link: https://medium.com/towards-artificial-intelligence/a-brief-summary-of-maths-behind-rnn-recurrent-neural-networks-b71bbc183ff
Preparing to write a book
How to evaluate a deep learning framework?
How reliable is the theoretical foundation of machine learning?
Andrew Ng's latest interview: AI centered on data
[Fundamentals of Machine Learning] The mathematical foundation behind optimization
Three consecutive views, monthly income of one million👇
