Understanding GNN (Graph Neural Networks)

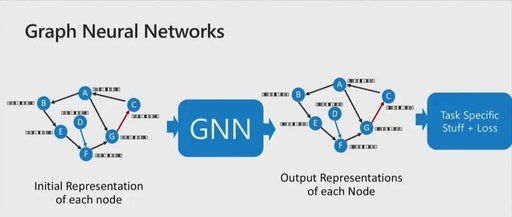
This article will cover the essence of GNN、GNNprinciples、GNNapplications in three aspects, allowing you to understand Graph Neural Networks (GNN) in one article.

Graph Neural Network (GNN)

1. The Essence of GNNEssence of GNN

The definition of GNN:GNN, or Graph Neural Network, is a deep learning model based on graph structures, specifically designed to handle graph data.

Definition of a graph:A graph is a mathematical structure composed of nodes (or vertices) and edges, used to represent the relationships between objects. Nodes represent entities, while edges represent connections between nodes.

Graph Information:

To describe the nodes, edges, or overall structure of a graph in more detail, we can store relevant information in these parts of the graph. Nodes can store attributes of entities, edges can store details about the relationships between nodes, and the entire graph can store global information.

This information helps to comprehensively understand the structure and meaning of the graph and provides a foundation for graph analysis and algorithm applications. In Graph Neural Networks, this information is typically input into the model as feature vectors or weight matrices, used to learn representations of nodes and graphs.

Graph Information

Graph Representation:The adjacency list and adjacency matrix are two common data structures used to represent graphs, describing the connection relationships between the vertices in the graph.

The adjacency list is a linked storage structure for graphs.Vertices of the graph are stored in a one-dimensional array, where each element points to the first adjacent point, making it easier to represent all adjacent points of a vertex using a linked list.

Adjacency List

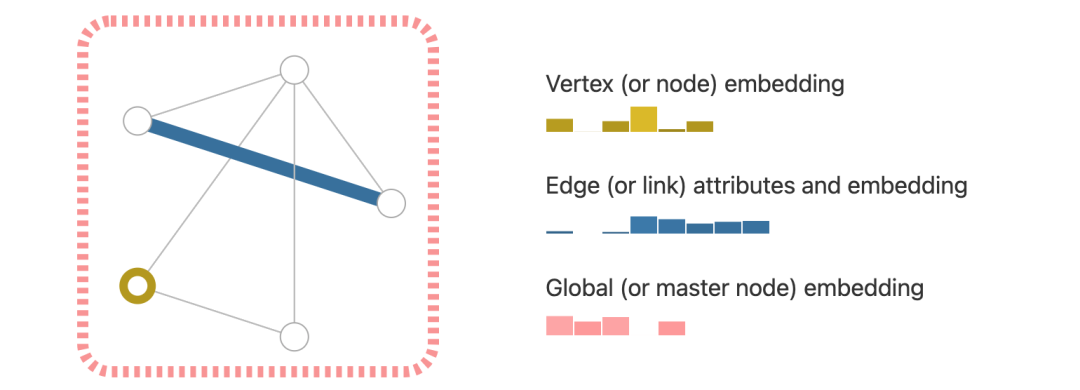
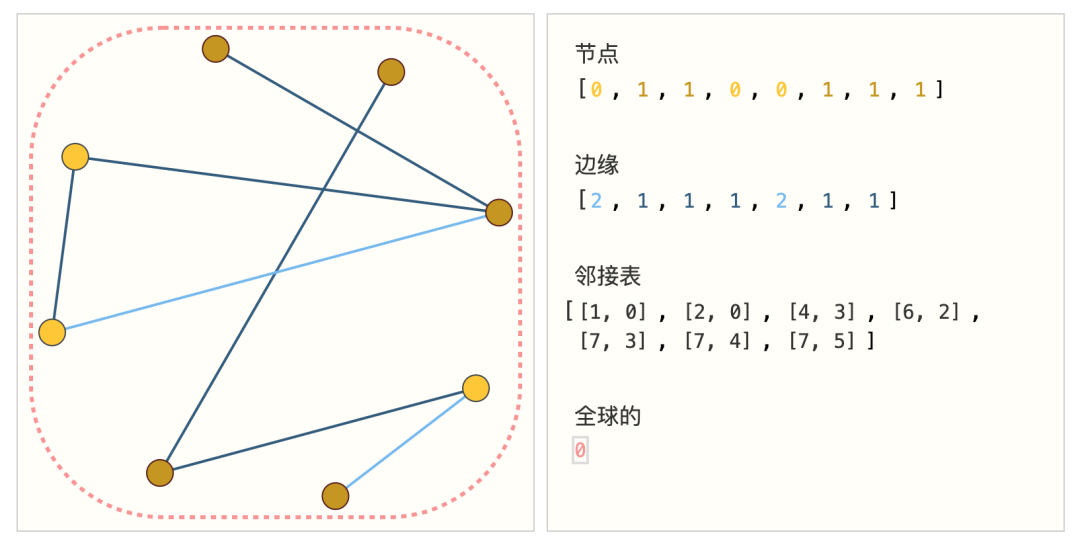
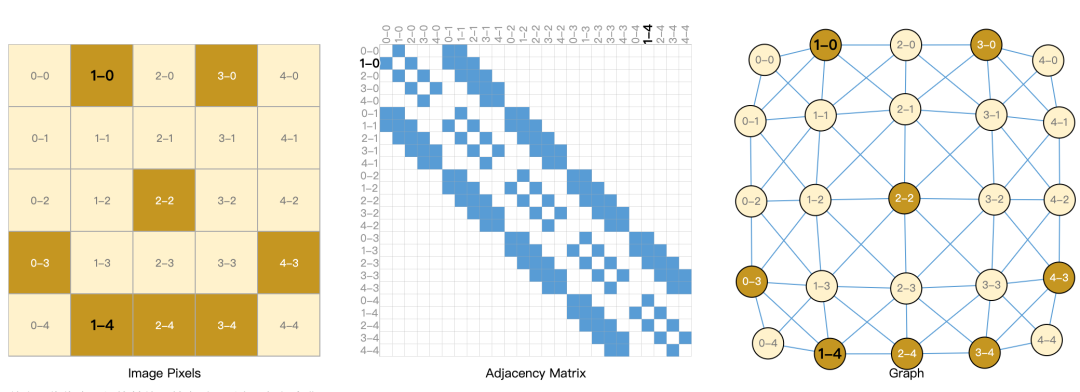
The adjacency matrix is a matrix representation of a graph.It uses a two-dimensional array to represent the relationships between the vertices in the graph. The rows and columns of the matrix correspond to the vertices in the graph, and the elements in the matrix represent the connection relationships between the vertices.

Adjacency Matrix

2. Principles of GNN

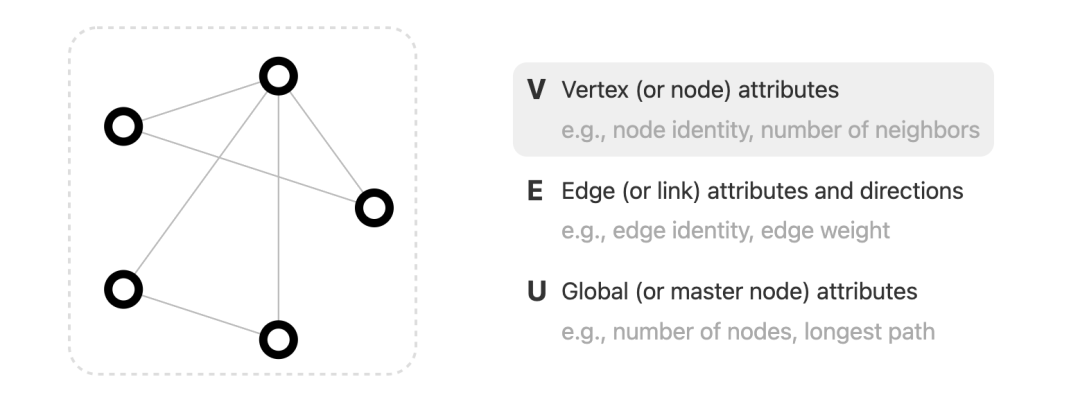
Architecture of GNN:GNN consists of three main functions,node function, edge function, and global function.These functions work together on the components of the graph (nodes, edges, and global context) to produce new embeddings or outputs.

1. Node function: Responsible for updating the node’s embedding by aggregating messages from neighboring nodes. The node function can be any differentiable function, such as a multilayer perceptron (MLP) or a recurrent neural network (RNN).

2. Edge function: Defines how to pass messages from edges to adjacent nodes, calculating messages based on the characteristics of the edge and the features of the two endpoints. The edge function can also be any differentiable function, such as a multilayer perceptron (MLP) or a recurrent neural network (RNN).

3. Global function: Generates a representation of the entire graph based on the information from all nodes and edges, used for graph-level prediction tasks. The global function can be achieved by aggregating the representations of all nodes or applying some form of pooling operation.

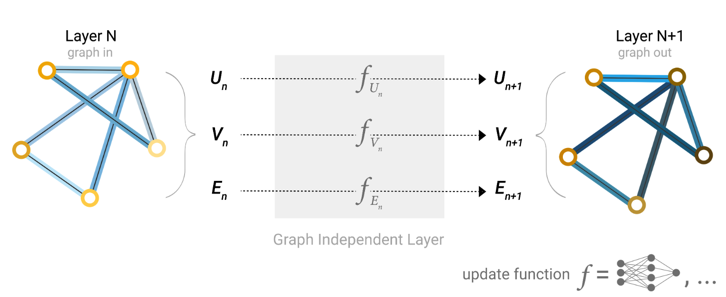
Architecture of GNN

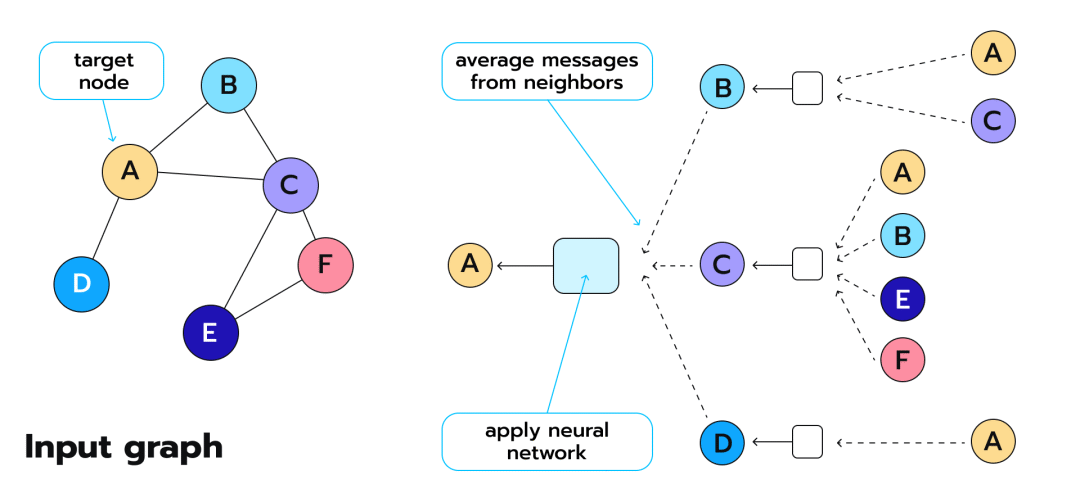
Working principle of GNN:In GNN layers, using pooling and message passing mechanisms, we can build more complex GNN models that can capture the connectivity and structural information of the graph to make more accurate predictions.

Message passing mechanism typically includes the following three key steps:

1. Message Generation: For each node in the graph, we first need to collect information (i.e., “messages”) from all its neighboring nodes. This is usually done by passing the embeddings (or features) of neighboring nodes through a function <span>g</span> (such as a linear transformation or a neural network) to generate messages. These messages can contain information about the features of neighboring nodes and their relationships with the central node.

2. Message Aggregation: Next, we need to aggregate all the messages received by the central node. This is typically done through an aggregation function (such as summation, average, max pooling, etc.). The purpose of the aggregation function is to combine multiple messages into a single vector that will represent the neighborhood information of the central node.

3. Node Update: Finally, we use the aggregated messages to update the embedding of the central node. This is usually achieved by passing the aggregated messages through an update function (such as a neural network). The role of the update function is to combine the current embedding of the central node with neighborhood information to produce a new, richer embedding.

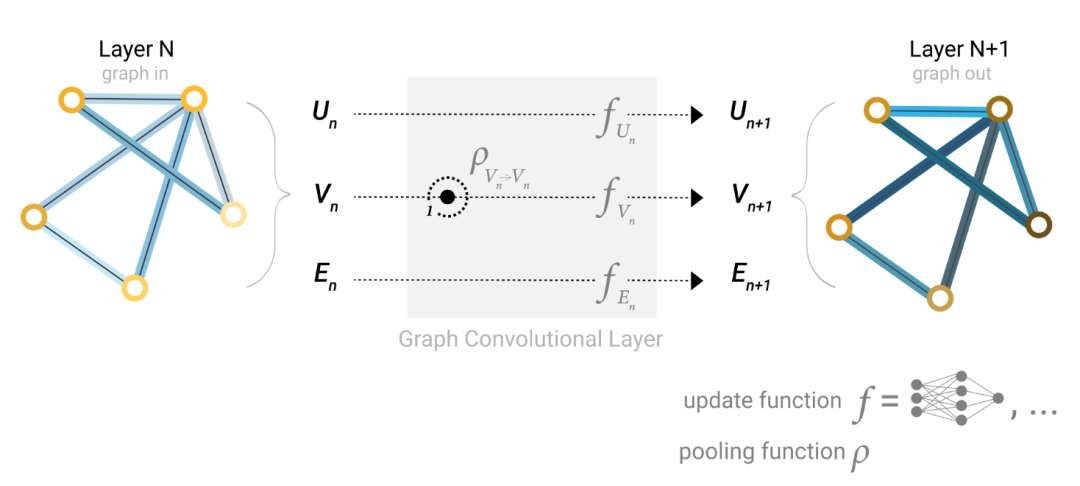
Working principle of GNN

Graph Attention Network (GAT):Another way to pass information between graph attributes is through attention.GAT is a model that introduces attention mechanisms based on Graph Neural Networks (GNN). This mechanism allows the model to dynamically assign different weights when aggregating information from neighboring nodes based on the relationships between nodes.

For each edge, interaction scores are calculated and normalized, which are used to weight node embeddings,helping the model better understand and capture information in the graph structure.Transformers can be seen as GNNs with attention mechanisms..

Graph Attention Network (GAT)

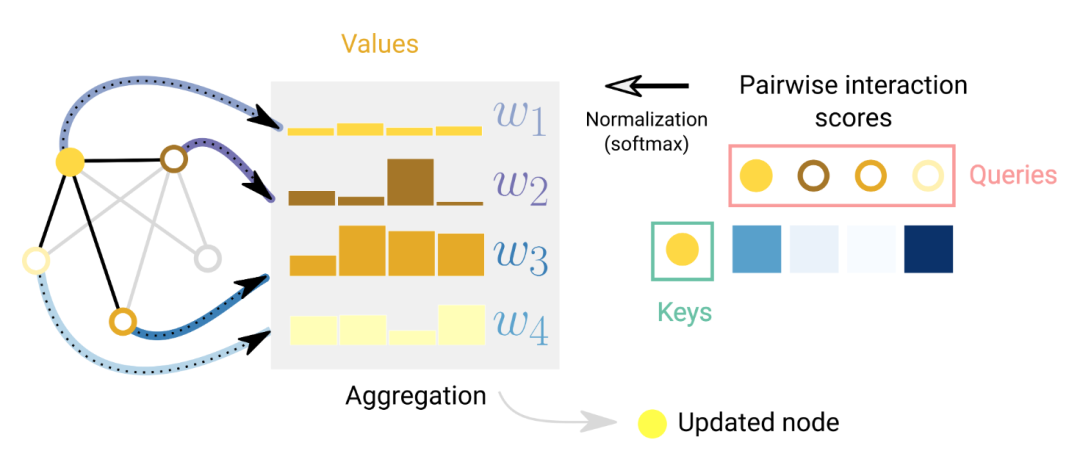
3. Applications of GNN

Social Network Analysis:Based on the integration of theories and methods from multiple disciplines such as information science, mathematics, sociology, management, and psychology, it aims to understand the formation of various social relationships, analyze behavioral characteristics, and study the laws of information dissemination.

Social Network Analysis

As a new generation AI model capable of processing graph data,GNN has unique advantages in handling irregular structured data in social networks and extracting hidden social network structures and patterns.

GNN ApplicationsSocial Network Analysis

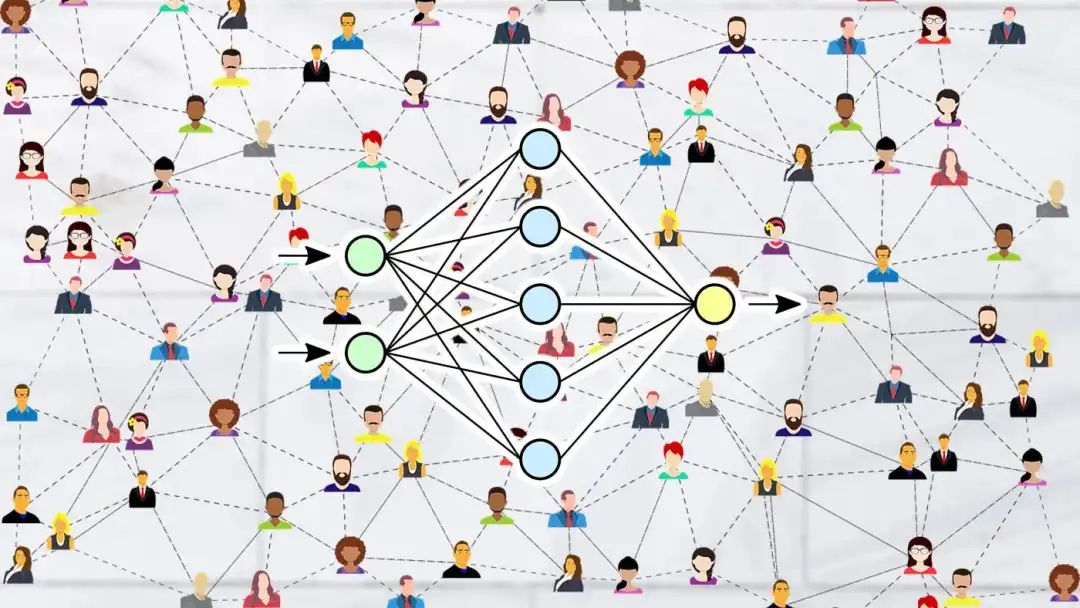
The following are four main applications of GNN in social network analysis:

Community Detection:GNN can discover hidden community structures in social networks by learning the connections and features between nodes. By embedding nodes, GNN can group similar nodes together, enabling effective community detection.

Community Detection

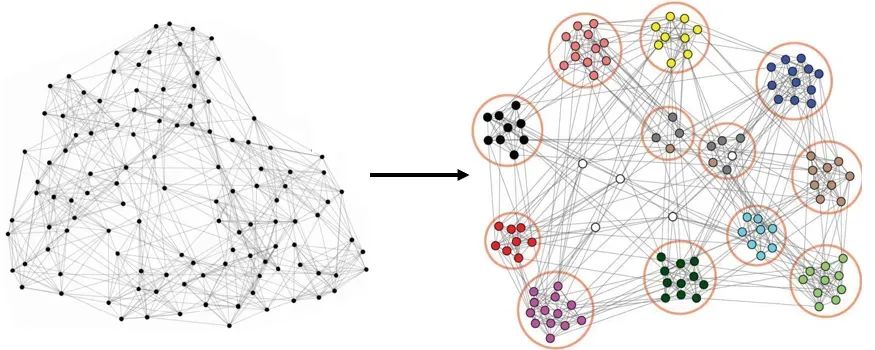
Link Prediction:In social networks, link prediction can be used for friend recommendations and predicting user behavior. By analyzing and modeling the graph structure, GNN can improve the accuracy and effectiveness of link prediction.

Link Prediction

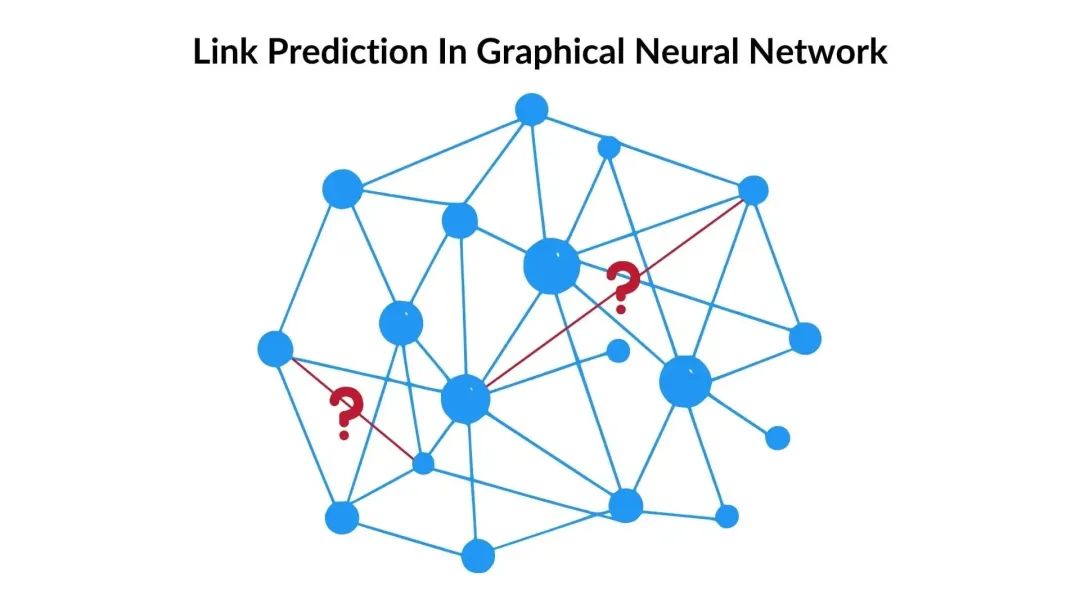
Node Classification:GNN can obtain the representation of nodes by iteratively updating the feature vectors of the nodes. Then, a linear classifier or other machine learning models can be applied to predict the categories of unlabeled nodes for classification and analysis in social networks.

Node Classification

Personalized Recommendations:GNN can mine user relationships to recommend content that better meets their needs and interests. By learning and analyzing social relationships between users, GNN can provide more accurate recommendation services.

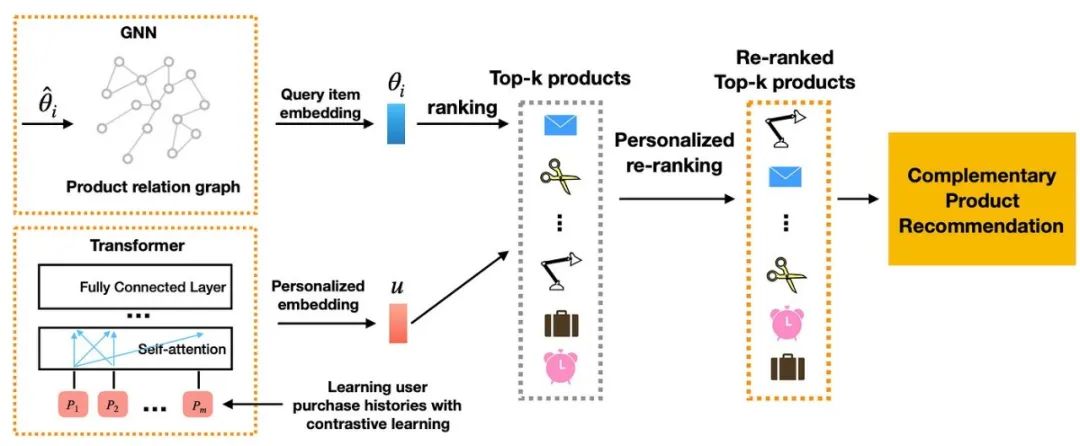
Personalized Recommendations