Understanding Convolutional Neural Networks (CNNs)

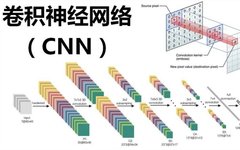
In the previous article “Convolution Operation and Its Applications in Image Processing”, we detailed the important role of convolution operations in image processing. Today, I will introduce the Convolutional Neural Network, which is the most widely used in neural networks.

A Convolutional Neural Network, or CNN, is an evolution of neural networks and is a milestone algorithm in the field of computer vision in recent years.

CNN was proposed by Yann LeCun from New York University in 1998. The essence of CNN is a multilayer perceptron, and its success is mainly attributed to its use of local connections and shared weights, which reduces the number of weights, making the network easier to optimize, while also lowering the risk of overfitting. In academia, neural networks are often seen as a typical “black box problem”; if its input is a feature vector of an object, then the output is the classification of that object, with the specific operation of classification performed by the computer, and the network architect remains unaware.

CNN networks typically consist of three parts: Neurons (Cell), Loss Function, and Activation Function.

Among them, neurons can be divided into input layer, hidden layer, and output layer; the loss function measures the discrepancy between the classification result and the true category after each network training and continuously updates the network parameters based on this, usually using softmax loss or SVM loss; the activation function usually transforms linear classification problems into nonlinear ones, allowing neural networks to better solve more complex problems, typically consisting of functions like sigmoid, tanh, and ReLU.

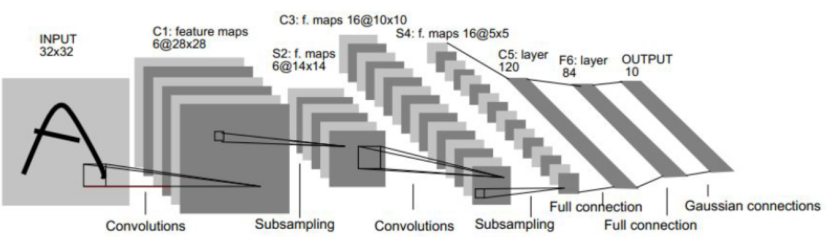
The convolutional layer and pooling layer of the CNN hidden layer are the core modules for implementing the feature extraction function of convolutional neural networks. This network model minimizes the loss function by using gradient descent to adjust the weight parameters of the network layer by layer, improving the accuracy of the network through frequent iterative training.

The low hidden layers of CNN consist of alternating convolutional layers and max pooling layers, while the high layers are fully connected layers corresponding to the hidden layers of traditional multilayer perceptrons and logistic regression classifiers. The input to the first fully connected layer is the feature maps obtained from the convolutional and subsampling layers. The final output layer is a classifier that can use logistic regression, softmax regression, or even support vector machines to classify the input images.

In issues such as object detection, object recognition, image segmentation, super-resolution, object tracking, and object retrieval, the recognition accuracy based on CNN algorithms is far superior to that of traditional algorithms.

(1) Input Layer

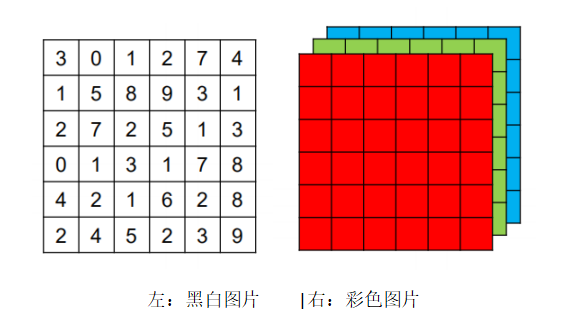
CNN is generally an artificial intelligence algorithm for image processing, and images are typically composed of several pixels, with the numbers in the image representing pixel brightness, where 0 is black and 255 is white. Therefore, a picture can be simplified into a multidimensional matrix composed of several numbers in the computer.

In the input layer of CNN, the input format retains the structure of the image itself. For black-and-white images, the input to CNN is a two-dimensional neuron; for RGB format (color) images, the input to CNN is a three-dimensional neuron (each color channel in RGB has its own matrix).

(2) Convolution Layer

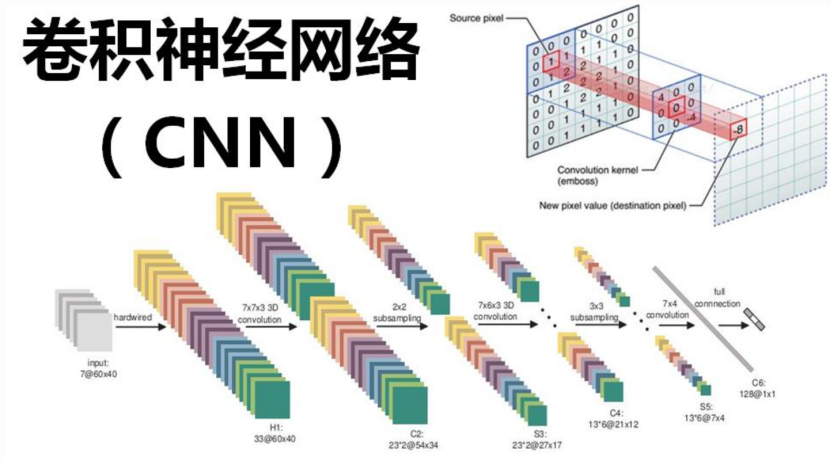
The convolution layer in CNN consists of a set of filters, which can be viewed as two-dimensional numerical matrices with customizable length and width. The following figure illustrates the convolution operation performed on a 4*4 two-dimensional black-and-white image, with a 3*3 filter.

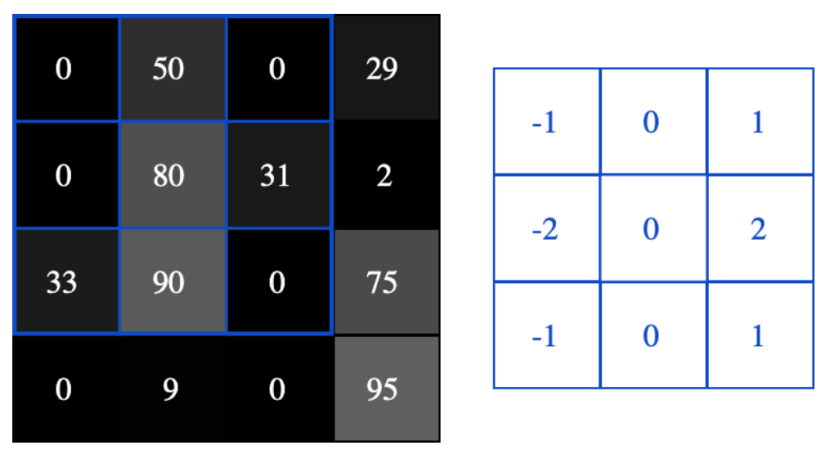
The specific steps of the convolution operation are as follows:

① Cover the filter over a position in the image;

② Multiply the values in the filter by the corresponding pixel values in the image;

③ Sum the products obtained above to get the value of the target pixel in the output image;

④ Move the filter a certain number of steps (Stride, which can be customized) to the right or down, and repeat this operation for all positions in the image.

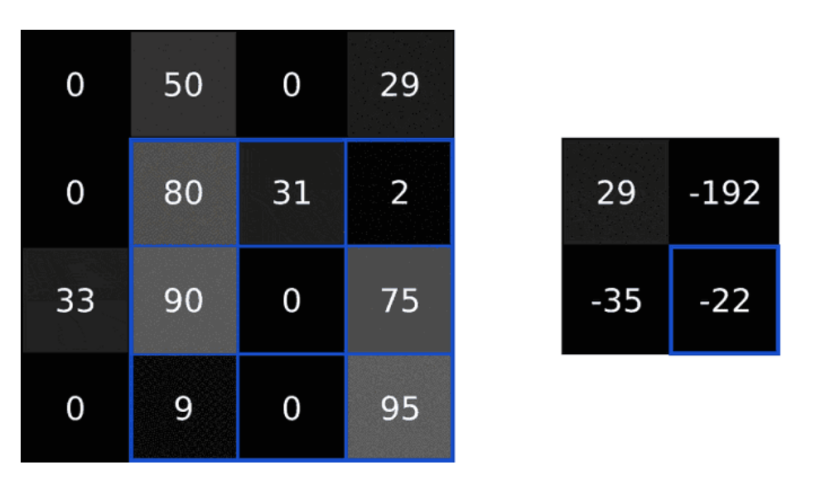
In the above example, multiplication is performed element by element between the overlapping image and filter elements, moving the filter from left to right and top to bottom, ultimately resulting in a 2*2 two-dimensional new matrix.

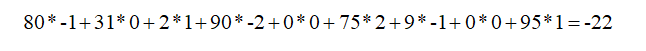
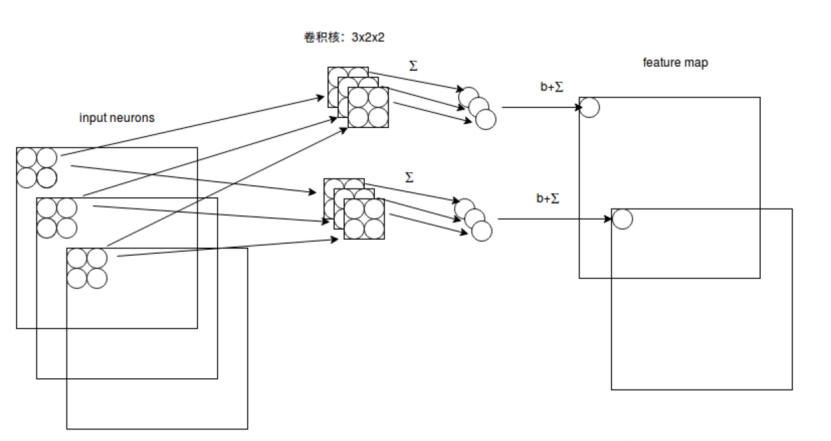
Similarly, if the input RGB image is a three-dimensional neuron, then the corresponding filter in the convolution layer is also three-dimensional, and the specific operation method is similar to the two-dimensional case, involving element-wise multiplication between overlapping elements and then summing, as shown in the following figure.

(3) Pooling Layer

The role of the convolution layer is generally to extract features from images, but when the dimensions of the feature map obtained from convolution are still relatively large, pooling layers can be used to perform dimensionality reduction on each feature map.

The pooling method also uses a filter (pooling matrix) for scanning, and during the scanning process, the stride length will also be involved, scanning from left to right, then moving down by the stride size, and scanning from left to right again.

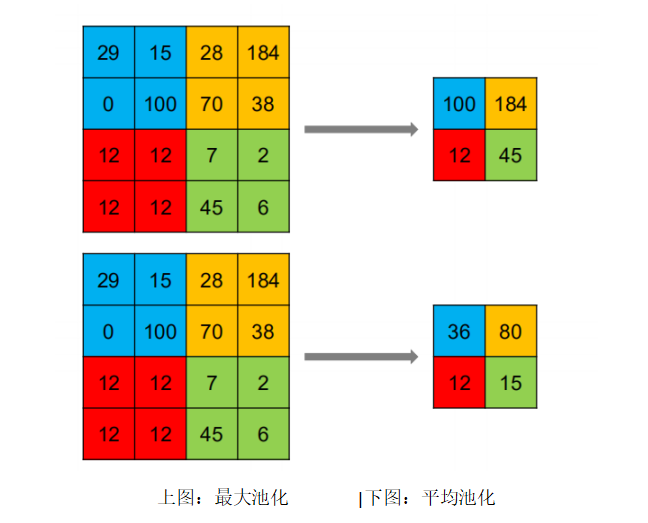
There are usually two methods for pooling: max pooling and average pooling.

Max Pooling: Takes the maximum value from the “pooling field” matrix.

Average Pooling: Takes the average value from the “pooling field” matrix.

(4) Fully Connected Layer and Output Layer

To finally obtain a one-dimensional number representing the classification of the image, further operations are required on the two-dimensional or three-dimensional vectors obtained from pooling, usually performed by the fully connected layer.

As the name suggests, all neurons in the fully connected layer are connected to the previous layer, and its main function is to refit features and reduce the loss of feature information. The main characteristic of the fully connected layer is that it has too many parameters, which can easily lead to overfitting, and a common solution is to use Dropout (randomly dropping some data).