Click the above “Beginner’s Visual Learning” to select to add Star Mark or “Pin”
Essential content delivered in real-time
In this article, the author visualizes 26 activation functions including ReLU and Sigmoid, along with relevant properties of neural networks, providing a great resource for understanding activation functions.
In neural networks, the activation function determines the output of nodes from a given input set, where non-linear activation functions allow the network to replicate complex non-linear behavior. As the vast majority of neural networks are optimized using some form of gradient descent, the activation functions need to be differentiable (or at least almost everywhere differentiable). Furthermore, complex activation functions may cause issues such as gradient vanishing or explosion. Therefore, neural networks tend to deploy several specific activation functions (identity, sigmoid, ReLU, and its variants).
Below are the illustrations of 26 activation functions and their first derivatives, with some neural network-related properties displayed on the right side of the graphs.
1. Step
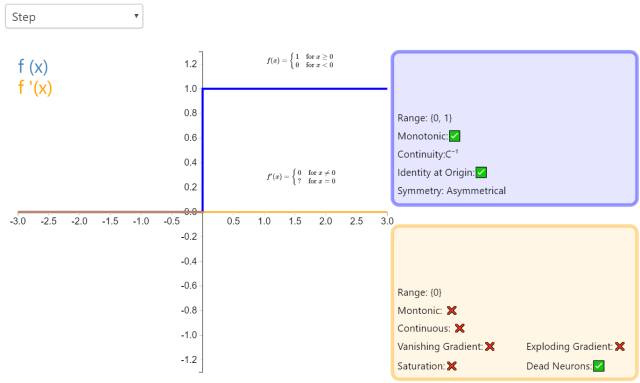
The Step activation function is more theoretical than practical, as it mimics the all-or-nothing property of biological neurons. It cannot be applied to neural networks because its derivative is 0 (except at the point where the derivative is undefined), which means gradient-based optimization methods are not feasible.
2. Identity
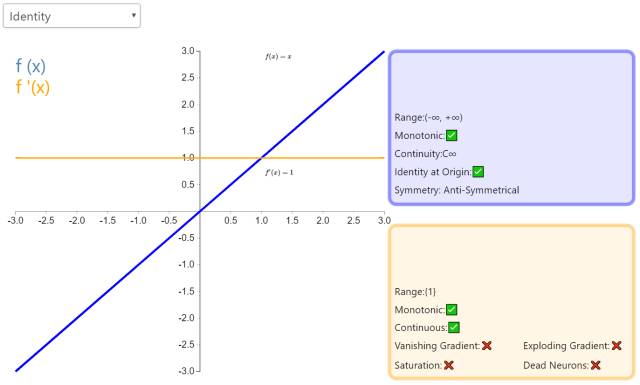
The Identity activation function outputs equal to its input. It is perfectly suited for tasks where the underlying behavior is linear (similar to linear regression). When non-linearity is present, using this activation function alone is insufficient, but it can still be used as an activation function for regression tasks at the final output node.
3. ReLU
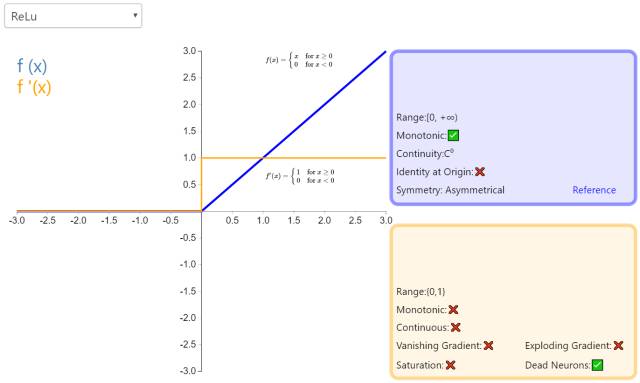
The Rectified Linear Unit (ReLU) is the most commonly used activation function in neural networks. It retains the biological inspiration of the step function (neurons only activate when input exceeds a threshold), but when the input is positive, the derivative is non-zero, allowing for gradient-based learning (although at x=0, the derivative is undefined). Using this function makes computations fast since neither the function nor its derivative involves complex mathematical operations. However, when the input is negative, the learning speed of ReLU may slow down significantly, even causing neurons to become inactive directly, as the input is less than zero and the gradient is zero, leading to weights not being updated and remaining silent throughout the rest of the training process.
4. Sigmoid
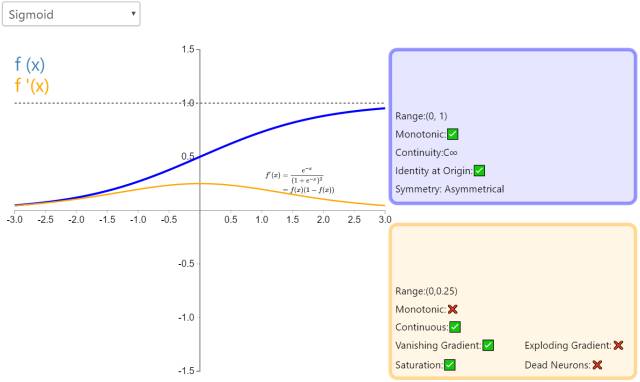
Sigmoid is well-known for its significant role in logistic regression, with a range between 0 and 1. The Logistic Sigmoid (or commonly referred to as Sigmoid) activation function introduces the concept of probability to neural networks. Its derivative is non-zero and easy to compute (it’s a function of its initial output). However, in classification tasks, sigmoid is gradually being replaced by the Tanh function as the standard activation function, as the latter is an odd function (symmetric about the origin).
5. Tanh
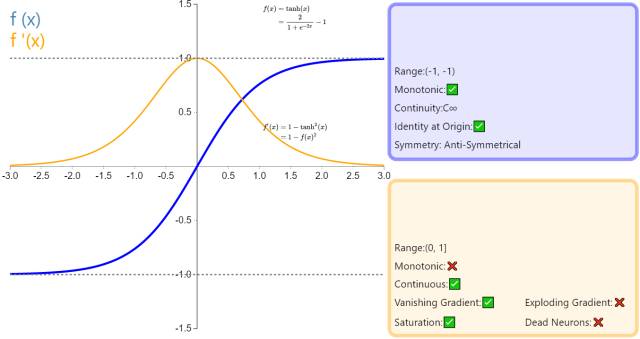
In classification tasks, the hyperbolic tangent function (Tanh) is gradually replacing the Sigmoid function as the standard activation function, possessing many characteristics favored by neural networks. It is fully differentiable, anti-symmetric, and has a symmetric center at the origin. To address slow learning and/or gradient vanishing issues, smoother variants of this function (log-log, softsign, symmetrical sigmoid, etc.) can be used.
6. Leaky ReLU
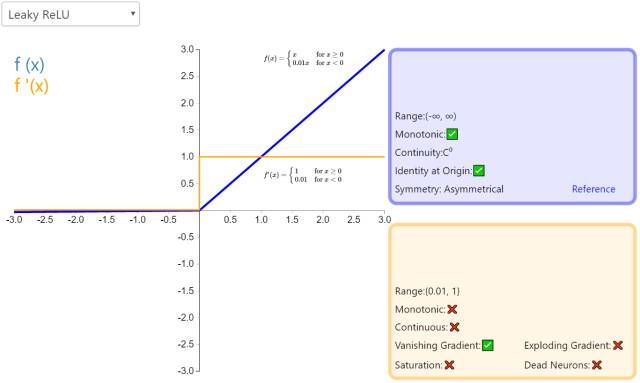
The Leaky ReLU, a classic (and widely used) variant of the ReLU activation function, has a small slope for negative input values. Since the derivative is never zero, this reduces the occurrence of silent neurons, allowing for gradient-based learning (although it may be slow).
7. PReLU
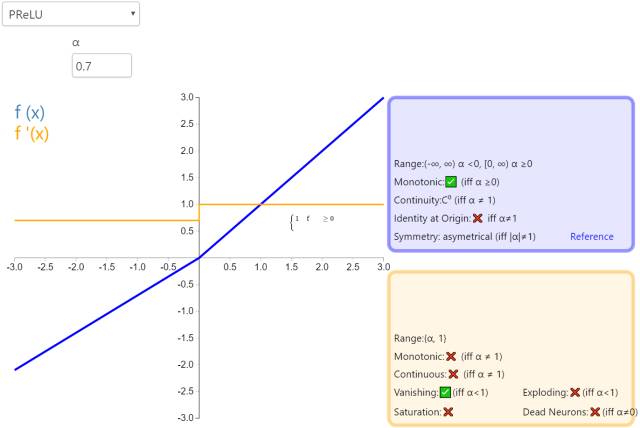
The Parametric Rectified Linear Unit (PReLU) is part of the ReLU family of activation functions. It shares some similarities with RReLU and Leaky ReLU, adding a linear term for negative input values. The key difference is that the slope of this linear term is learned during model training.
8. RReLU
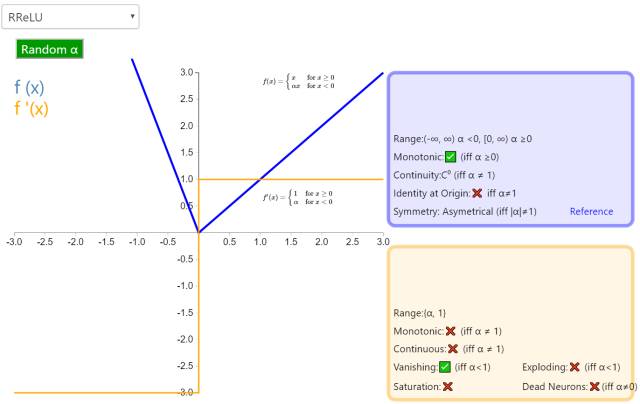
The Randomized Leaky Rectified Linear Unit (RReLU) is also part of the ReLU family of activation functions. Similar to Leaky ReLU and PReLU, it adds a linear term for negative input values. The key difference is that the slope of this linear term is randomly assigned at each node (usually following a uniform distribution).
9. ELU
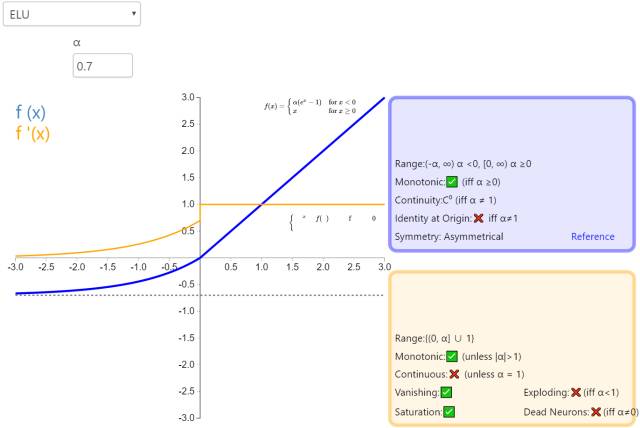
The Exponential Linear Unit (ELU) is also part of the ReLU family of activation functions. Similar to PReLU and RReLU, it adds a non-zero output for negative input values. Unlike other rectified activation functions, it includes a negative exponential term, which prevents silent neurons from appearing and allows the derivative to converge to zero, thus improving learning efficiency.
10. SELU
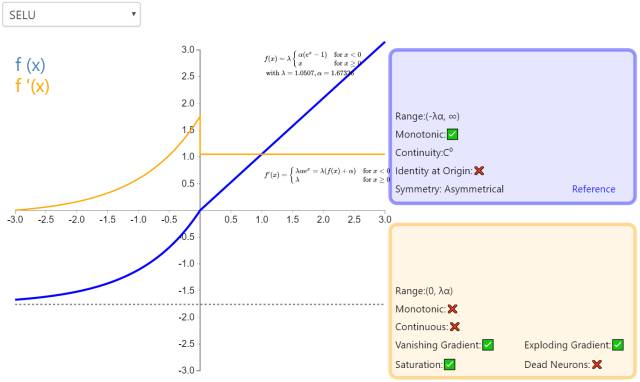
The Scaled Exponential Linear Unit (SELU) is a variant of the Exponential Linear Unit (ELU). Here, λ and α are fixed values (1.0507 and 1.6726, respectively). The implications of these values (zero mean/unit variance) form the basis of self-normalizing neural networks (SNN).
11. SReLU
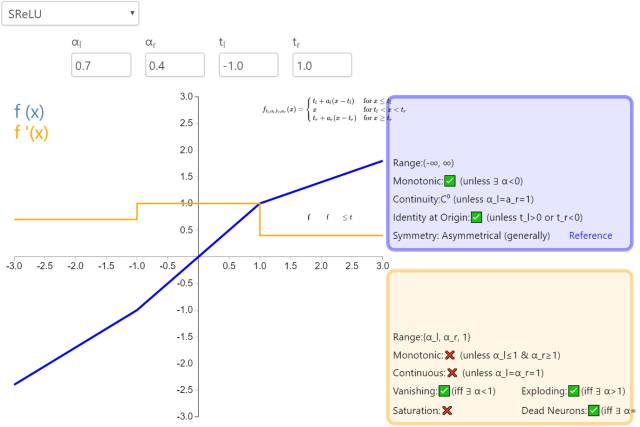
The S-shaped Rectified Linear Activation Unit (SReLU) belongs to the family of rectified activation functions represented by ReLU. It consists of three piecewise linear functions. The slopes of the two functions and the intersection points will be learned during model training.
12. Hard Sigmoid
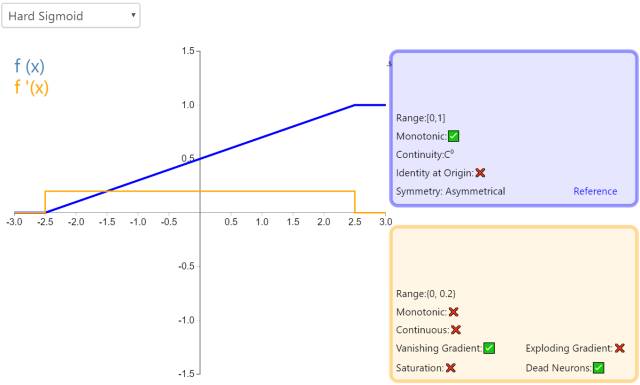
Hard Sigmoid is a piecewise linear approximation of the Logistic Sigmoid activation function. It is easier to compute, which speeds up the learning process, although the zero derivative at the first point may lead to silent neurons/slow learning rates (see ReLU).
13. Hard Tanh
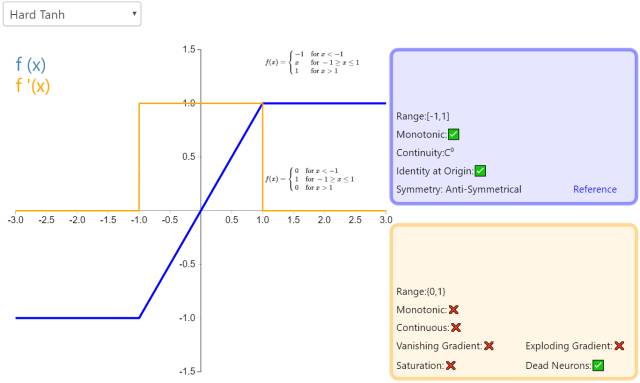
Hard Tanh is a piecewise linear approximation of the Tanh activation function. Comparatively, it is easier to compute, which speeds up the learning process, although the zero derivative at the first point may lead to silent neurons/slow learning rates (see ReLU).
14. LeCun Tanh
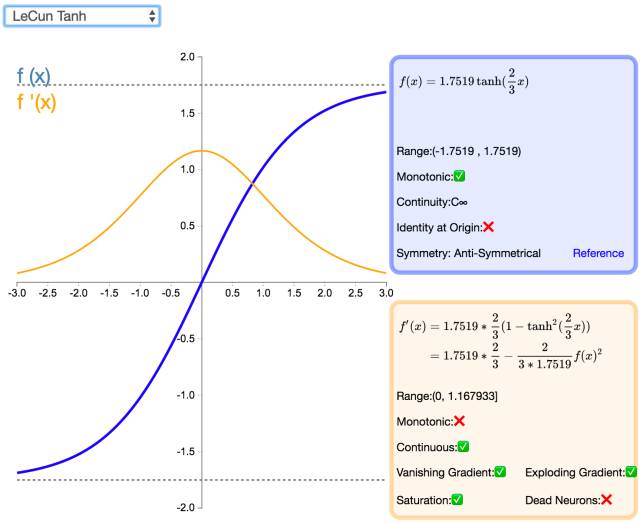
The LeCun Tanh (also known as Scaled Tanh) is an extended version of the Tanh activation function. It has several properties that can improve learning: f(± 1) = ±1; the second derivative is maximized at x=1; and the effective gain is close to 1.
15. ArcTan
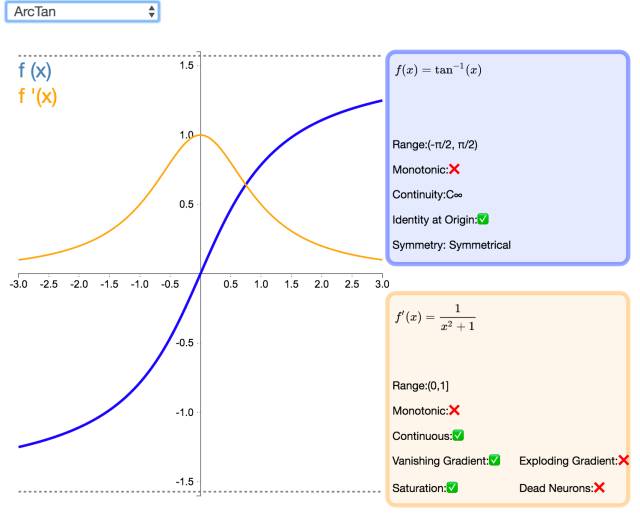
Visually similar to the hyperbolic tangent (Tanh) function, the ArcTan activation function is flatter, making it clearer than other hyperbolic functions. By default, its output range is between -π/2 and π/2. Its derivative approaches zero more slowly, indicating higher learning efficiency. However, this also means that computing the derivative is more expensive than Tanh.
16. Softsign
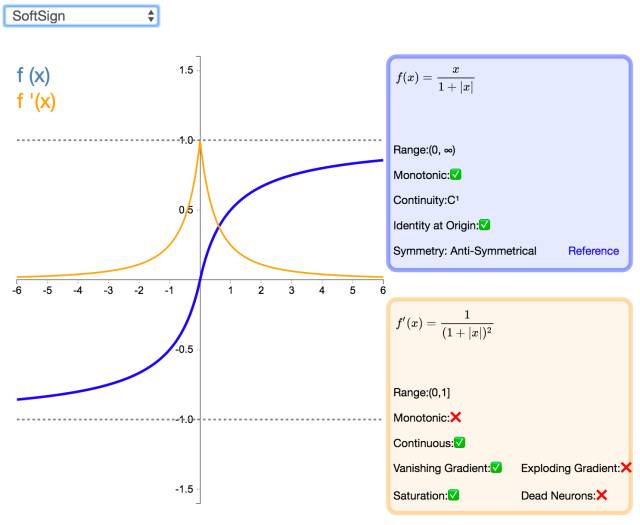
The Softsign activation function is another alternative to the Tanh activation function. Like Tanh, Softsign is anti-symmetric, zero-centered, differentiable, and returns values between -1 and 1. Its flatter curve and slower descending derivative indicate it can learn more efficiently. On the other hand, computing the derivative is more complicated than Tanh.
17. SoftPlus
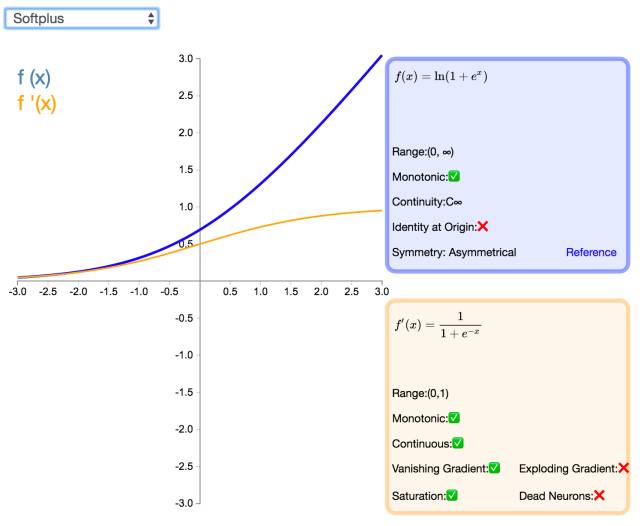
As a good alternative to ReLU, SoftPlus can return any value greater than 0. Unlike ReLU, the derivative of SoftPlus is continuous, non-zero, and ubiquitous, preventing silent neurons from appearing. However, another difference from ReLU is its asymmetry and non-zero centering, which may hinder learning. Additionally, since the derivative often falls below 1, gradient vanishing issues may also arise.
18. Signum

The Signum activation function (or abbreviated as Sign) is an extended version of the binary step activation function. Its range is [-1,1], with the origin value being 0. Despite lacking the biological motivation of the step function, Signum remains anti-symmetric, which is a favorable characteristic for activation functions.
19. Bent Identity
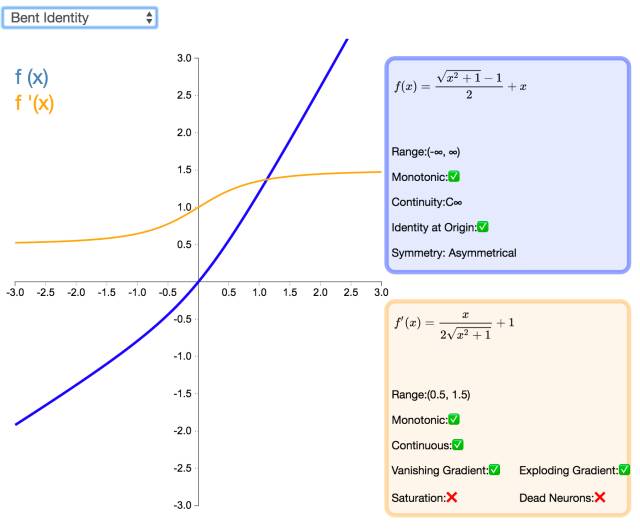
The Bent Identity activation function is a compromise choice between Identity and ReLU. It allows for non-linear behavior, although its non-zero derivative effectively enhances learning and overcomes the silent neuron issue associated with ReLU. Since its derivative can return values on either side of 1, it may be susceptible to gradient explosion and vanishing effects.
20. Symmetrical Sigmoid
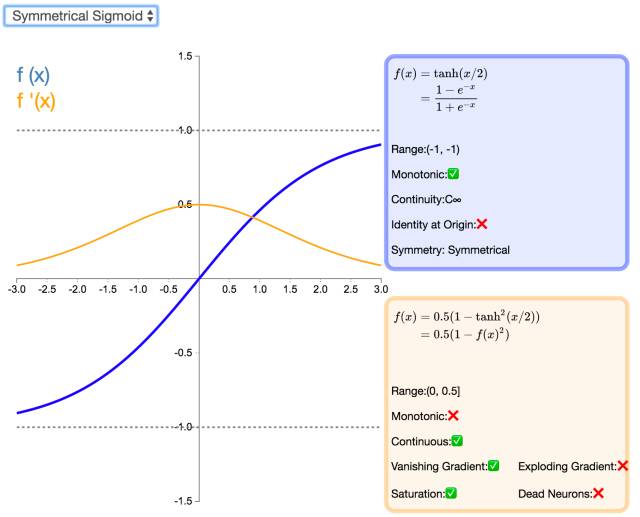
The Symmetrical Sigmoid is another variant of the Tanh activation function (in fact, it is equivalent to Tanh with halved inputs). Like Tanh, it is anti-symmetric, zero-centered, differentiable, and has a range between -1 and 1. Its flatter shape and slower descending derivative suggest it can learn more effectively.
21. Log Log
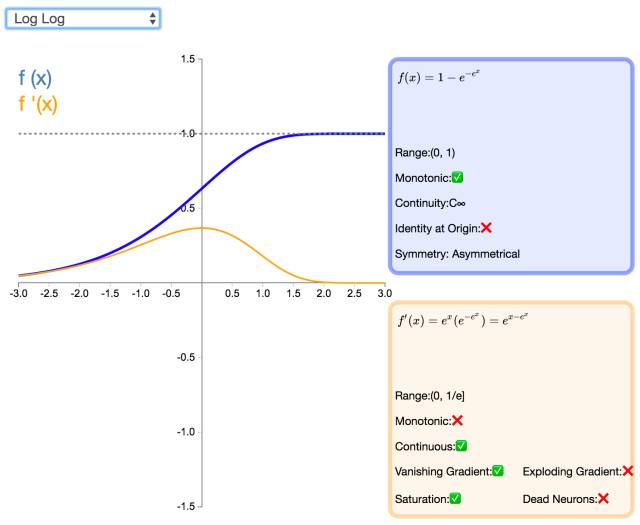
The Log Log activation function (as seen in the graph f(x), this function is a nested exponential function with base e) has a range of [0,1], and the Complementary Log Log activation function has the potential to replace the classic Sigmoid activation function. This function saturates faster and has a zero point value higher than 0.5.
22. Gaussian
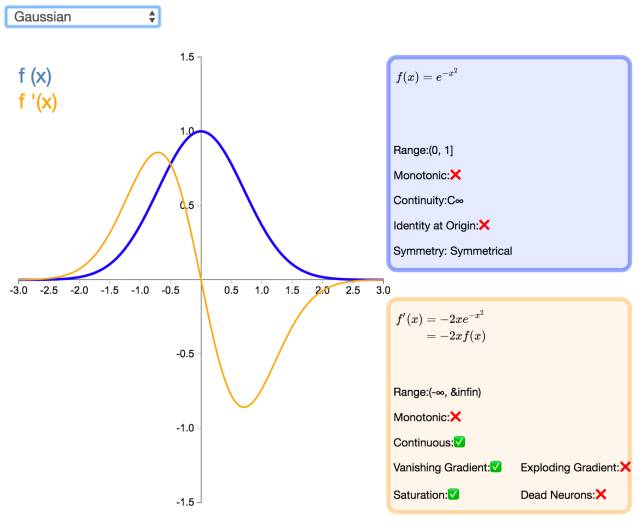
The Gaussian activation function is not the commonly used Gaussian kernel function in Radial Basis Function Networks (RBFN). This function is not very popular in multilayer perceptron models. It is differentiable everywhere and is an even function, but the first derivative converges to zero quickly.
23. Absolute
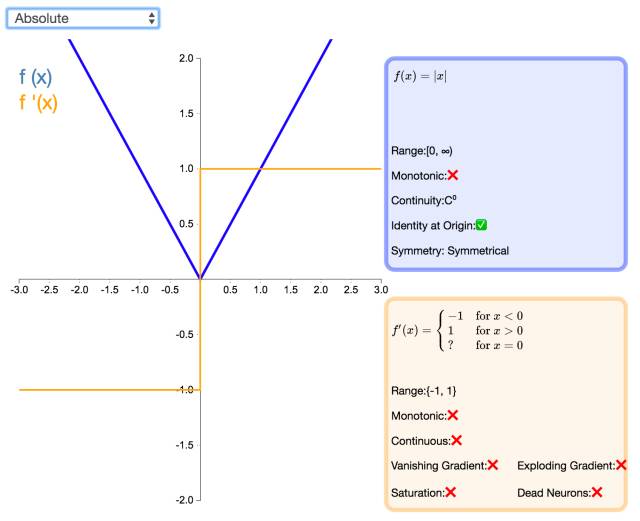
As the name suggests, the Absolute activation function returns the absolute value of the input. The derivative of this function is defined everywhere except at the zero point, and the magnitude of the derivative is 1 everywhere. This activation function will never experience gradient explosion or vanishing.
24. Sinusoid
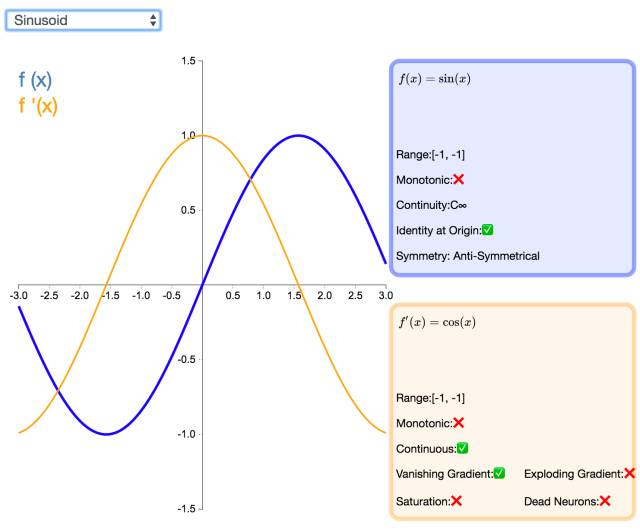
Similar to the cosine function, the Sinusoid (or simple sine function) activation function introduces periodicity into neural networks. This function has a range of [-1,1] and is continuously differentiable. Furthermore, the Sinusoid activation function is an odd function symmetric about the origin.
25. Cos
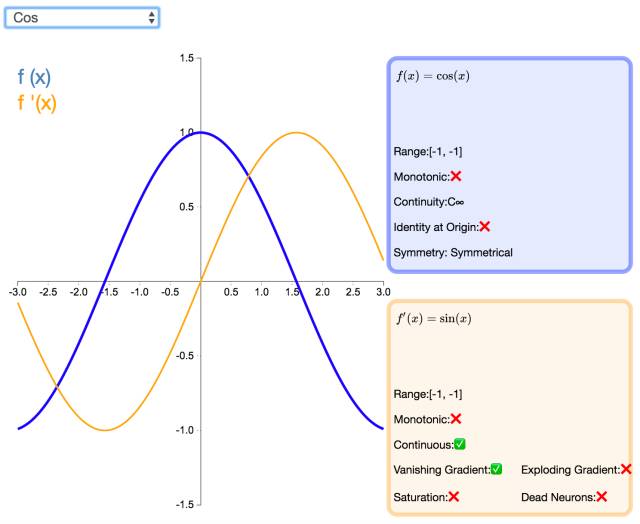
Like the sine function, the cosine activation function (Cos/Cosine) introduces periodicity into neural networks. Its range is [-1,1], and its derivative is continuously differentiable. Unlike the Sinusoid function, the cosine function is an even function that is not symmetric about the origin.
26. Sinc
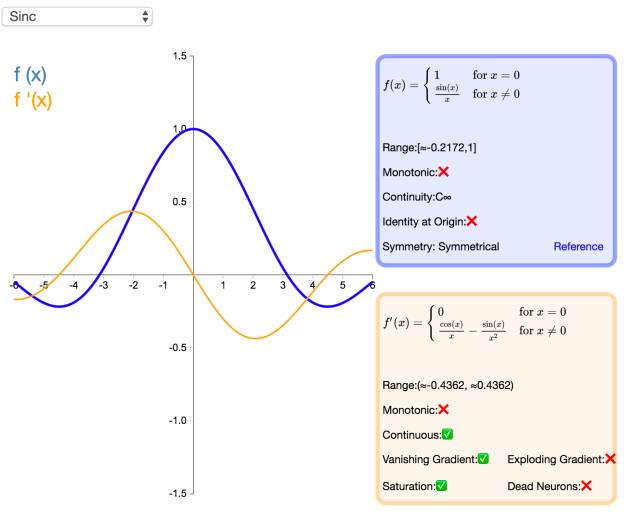
The Sinc function (full name Cardinal Sine) is particularly important in signal processing, as it characterizes the Fourier transform of the rectangular function. As an activation function, its advantages lie in its differentiability everywhere and symmetry, although it is prone to gradient vanishing issues.
Original link:https://dashee87.github.io/data%20science/deep%20learning/visualising-activation-functions-in-neural-networks/
Good news!
Beginner’s Visual Learning Knowledge Circle
Is now open to the public👇👇👇
Download 1: OpenCV-Contrib Extension Module Chinese Version Tutorial
Reply "Extension Module Chinese Tutorial" in the background of the "Beginner's Visual Learning" public account to download the first Chinese version of the OpenCV extension module tutorial on the internet, covering more than 20 chapters including extension module installation, SFM algorithms, stereo vision, object tracking, biological vision, super-resolution processing, etc.
Download 2: Python Visual Practical Project 52 Lectures
Reply "Python Visual Practical Project" in the background of the "Beginner's Visual Learning" public account to download 31 visual practical projects including image segmentation, mask detection, lane line detection, vehicle counting, eyeliner addition, license plate recognition, character recognition, emotion detection, text content extraction, facial recognition, etc., to help quickly learn computer vision.
Download 3: OpenCV Practical Project 20 Lectures
Reply "OpenCV Practical Project 20 Lectures" in the background of the "Beginner's Visual Learning" public account to download 20 practical projects based on OpenCV, achieving advanced learning of OpenCV.
Group Chat
Welcome to join the public account reader group to exchange with peers. Currently, there are WeChat groups for SLAM, 3D vision, sensors, autonomous driving, computational photography, detection, segmentation, recognition, medical imaging, GAN, algorithm competitions, etc. (will gradually subdivide in the future). Please scan the WeChat number below to join the group, and note: "Nickname + School/Company + Research Direction", for example: "Zhang San + Shanghai Jiao Tong University + Visual SLAM". Please note the format, otherwise, it will not be approved. After successful addition, you will be invited into related WeChat groups based on research direction. Please do not send advertisements in the group, otherwise, you will be removed from the group, thank you for your understanding~
