Cite this article

REN Hongbo, WU Qiong, WANG Xiangyu, et al. Uncertainty Plan of a Zero-carbon Energy System Based on LSTM Quantile Regression[J]. Journal of Shanghai University of Electric Power, 2023, 39(2):149-157.

Abstract

The zero-carbon energy system is an effective way to promote the construction of a clean and low-carbon energy system and achieve carbon neutrality. However, the intermittence and volatility of wind, solar, and other renewable energy generation pose significant challenges to the rational planning and scientific allocation of zero-carbon energy systems. Based on this, an uncertainty programming method for zero-carbon energy systems based on LSTM quantile regression is proposed. First, the physical structure of the zero-carbon energy system is constructed, and typical equipment in the system is modeled. Then, based on the interval number theory, an interval prediction model for photovoltaic power generation based on LSTM quantile regression is constructed. Next, taking the minimum annual total economic cost as the objective function, a mixed-integer linear programming model that can optimize the equipment configuration and operational strategy is established. Finally, through typical case analysis, the feasibility of the proposed model in addressing the uncertainty planning of zero-carbon energy systems is verified.

Keywords

zero-carbon energy system; uncertainty; LSTM quantile regression; optimal planning

With the reduction of global fossil energy and the increasing prominence of environmental issues, countries around the world have introduced diverse policies to promote the application of renewable energy. By the end of 2020, China’s installed capacity of photovoltaic and wind power reached 250 million kW and 280 million kW respectively. Accelerating the promotion of a multi-energy complementary integrated energy system dominated by new energy has become a powerful measure to achieve carbon neutrality and promote China’s energy transition. Renewable energy generation is gradually transitioning from auxiliary power sources to primary energy sources. Compared with traditional energy systems, the optimal configuration and reasonable operational scheduling of complex equipment in integrated energy systems are core factors for achieving stable and efficient system operation. Literature has optimized the equipment configuration of integrated energy systems containing wind, solar, and natural gas based on energy hubs as the basic structure. To fundamentally address ecological and environmental issues caused by fossil energy and to promote the achievement of dual carbon goals, some scholars have proposed constructing zero-carbon integrated energy systems. Literature has proposed and constructed a zero-carbon energy power system based on wind-solar-biogas, optimizing the system with economic efficiency, power quality, and supply reliability as objectives. Literature has comprehensively considered the resource endowment and user load demand characteristics in remote rural areas, proposing a modeling and optimization design framework for off-grid zero-carbon energy systems powered by solar energy, wind energy, and biomass energy. As core elements of zero-carbon energy systems, the output of renewable energy sources such as wind and solar is characterized by significant intermittence and volatility; however, existing integrated energy planning solutions have not delved deeply into this issue.

Regarding the prediction of photovoltaic and wind power outputs, numerous studies have been conducted both domestically and internationally. In recent years, scholars have begun to explore the uncertainty issues. Literature has utilized Latin hypercube sampling and K-means clustering to obtain typical scenarios of wind power, effectively describing the uncertainty characteristics of wind power output. Literature has constructed a stochastic optimization scheduling model based on multi-scenario technology with the goal of minimizing expected operating costs across multiple scenarios; however, it requires high precision in probability distribution functions and substantial historical data support. Interval number theory offers a simple modeling approach for addressing the uncertainty of renewable energy, without the need for probabilistic distribution relationships of uncertain parameters. Literature has used interval numbers to describe the uncertainty of photovoltaic output and load, establishing a regional integrated energy system’s day-ahead economic optimization scheduling model based on interval linear programming, considering multi-energy complementarity, grid interconnection, and environmental benefits. Literature has established a bi-level optimization model based on particle swarm optimization-interval linear programming, studying the uncertainty of renewable energy and purchase energy prices within the system. In summary, there have been no related reports exploring the impact of uncertainty on the planning of zero-carbon energy systems primarily based on photovoltaic and wind energy.

This paper utilizes interval number theory to establish an uncertainty optimization planning method for zero-carbon energy systems based on Long Short-Term Memory (LSTM) quantile regression. First, a physical structure of a zero-carbon integrated energy system containing various zero-carbon energy technologies is constructed, and typical equipment within the system is mathematically modeled. Second, an interval prediction model for photovoltaic output uncertainty is established, and a mixed-integer linear programming model for zero-carbon energy systems is constructed with the objective of minimizing the annual total economic cost of the system. Finally, the feasibility and effectiveness of the constructed optimization model are verified through typical case analysis.

1 Zero-Carbon Integrated Energy System

1.1 Physical Structure of Zero-Carbon Energy System

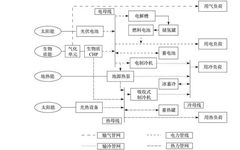
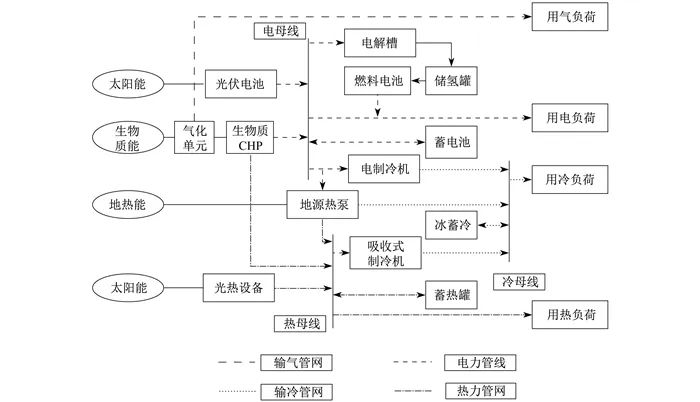
Constructing a clean energy system characterized by zero carbon emissions relies on zero-carbon energy technologies such as solar energy, wind energy, biomass energy, and green hydrogen energy to meet the diverse load demands for cooling, heating, and electricity. Combining the integrated energy system’s source-network-load-storage characteristics, the physical structure of the zero-carbon energy system is determined as shown in Figure 1. Here, the electrical load is primarily supplied by biomass combined heat and power (CHP) units, photovoltaic panels, and fuel cells; the thermal load is mainly supplied by the waste heat from biomass CHP, solar collectors, and ground source heat pumps; the cooling load is mainly supplied by electric chillers, absorption chillers, and ground source heat pumps. Energy storage devices such as batteries, thermal storage tanks, and ice storage equipment can also meet user load demands. Excess electrical energy that cannot be stored by battery equipment can be stored in hydrogen tanks through electrolysis of water using electrolyzers, for subsequent power generation by fuel cells.

1.2 Equipment Models of Zero-Carbon Energy System

1.2.1 Power Supply Equipment Model

The biomass CHP unit generates electricity through the pyrolysis and gasification of biomass fuel followed by combustion. At any moment t, the relationship between the terminal electrical energy output and energy input of the biomass CHP unit can be expressed as

Where: P_t^BCHP – the power generation of the biomass CHP unit at time t;

m_t^BM – the biomass fuel consumption at time t;

L_BM – the lower heating value of biomass fuel;

η^BCHP – the power generation efficiency of the biomass CHP unit.

The photovoltaic panel’s output mainly depends on local solar radiation, and its mathematical model can be expressed as

Where: P_t^PV – the photovoltaic power generation at time t;

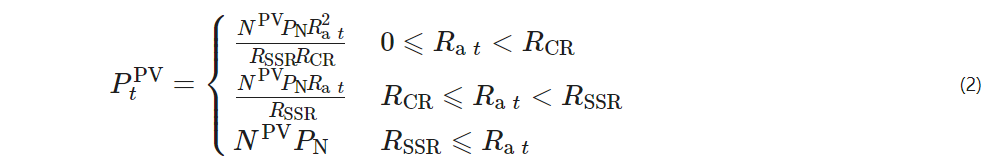
N^PV – the number of photovoltaic panels;

P_N – the rated power of each photovoltaic panel;

R_{a t} – the local solar radiation intensity at time t;

R_SSR – standard solar radiation intensity;

R_CR – specific radiation intensity.

Electrolyzer equipment can utilize excess electrical energy to electrolyze water to produce hydrogen, while fuel cells can generate electricity using hydrogen. Their mathematical models can be expressed as

Where: m_{t, H2}^ELZ – the mass of hydrogen produced by the electrolyzer at time t;

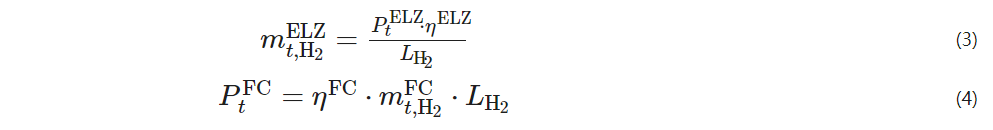
P_t^ELZ – the electrical energy consumed by the electrolyzer at time t;

η^ELZ – the hydrogen production efficiency of the electrolyzer;

L_H2 – the lower heating value of hydrogen;

P_t^FC – the power generation of the fuel cell at time t;

η^FC – the power generation efficiency of the fuel cell;

m_{t, H2}^FC – the amount of hydrogen consumed by the fuel cell at time t.

1.2.2 Heating Equipment Model

The mathematical model of the ground source heat pump can be expressed as

Where: H_t^GSHP, C_t^GSHP – the heating and cooling output of the ground source heat pump at time t;

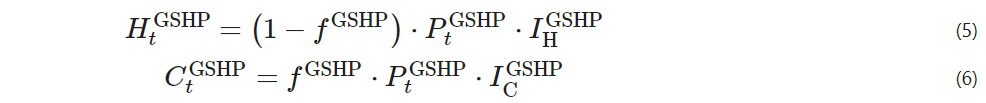
f^GSHP – takes 0 or 1, indicating that the ground source heat pump cannot simultaneously heat and cool;

P_t^GSHP – the electrical power input to the ground source heat pump at time t;

I_H^GSHP, I_C^GSHP – the heating and cooling energy efficiency coefficients of the ground source heat pump.

Solar collectors can convert solar radiation energy into thermal energy, and their mathematical model can be expressed as

Where: H_t^PT – the thermal output of the solar collector at time t;

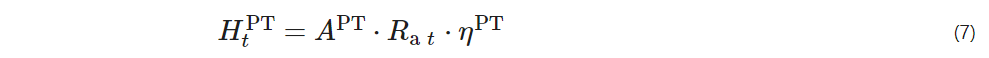
A^PT – the area of the collector panels;

η^PT – the efficiency of the solar collector.

1.2.3 Cooling Equipment Model

The mathematical model of the electric chiller can be expressed as

Where: C_t^ER – the cooling output of the electric chiller at time t;

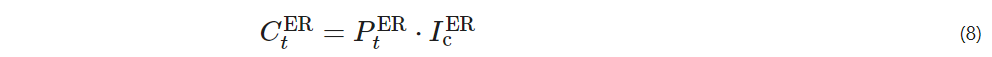
P_t^ER – the electrical energy consumed by the electric chiller at time t;

I_c^ER – the cooling performance coefficient of the electric chiller.

The absorption chiller relies on an absorber-generator to convert thermal energy into cooling load, which can be expressed as

Where: C_t^AC – the cooling output of the absorption chiller at time t;

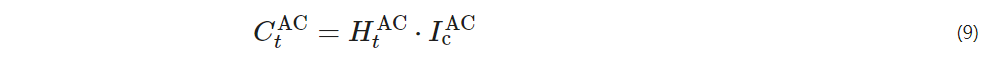
H_t^AC – the thermal input to the absorption chiller at time t;

I_c^AC – the performance coefficient of the absorption chiller.

1.2.4 Energy Storage Equipment Model

The mathematical models of energy storage, cooling/thermal storage, and hydrogen storage equipment are similar, and some losses will occur during the storage process. Taking hydrogen storage equipment as an example, at any moment, the state of the hydrogen storage device is equivalent to the sum of the previous moment’s hydrogen tank state value and the net value of hydrogen stored or released during the current time period. Its mathematical model can be expressed as

Where: G_t+Δt^HST, G_t^HST – the hydrogen storage amount in the tank at times (t+Δt) and t;

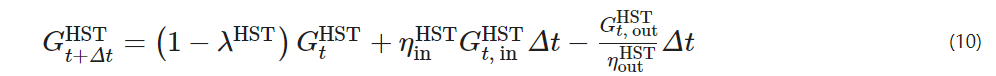
λ^HST – the self-discharge rate of the hydrogen tank;

η_in^HST, η_out^HST – the storage and release efficiency of the hydrogen tank;

G_{t, in}^HST, G_{t, out}^HST – the amount of hydrogen stored and released at time t.

2 Interval Prediction Model for Renewable Energy Generation

2.1 Interval Linear Programming

Interval linear programming applies interval number theory to linear programming and involves a class of linear programming where the objective function or constraints contain interval numbers. Using interval numbers to describe the uncertainty of photovoltaic output, its formula is

Where: P_t^PV – the actual output of photovoltaic energy at time t;

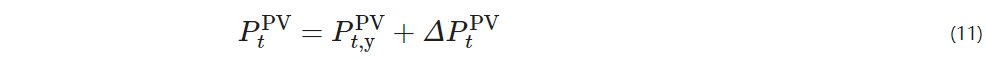
P_{t, y}^PV – the predicted value of photovoltaic output;

ΔP_t^PV – the prediction error value of photovoltaic output.

2.2 LSTM Quantile Regression Model

2.2.1 Quantile Regression

Regression analysis is a predictive modeling technique. Traditional regression analysis reflects the relationship between independent and dependent variables’ conditional expectations, but it is difficult to clearly reflect the situation where variable data is widely dispersed or asymmetrically distributed. The series of photovoltaic power generation often presents an asymmetric distribution, and traditional regression analysis cannot accurately analyze the influencing factors of the dependent variable. Quantile regression, based on traditional regression analysis that obtains the central trend of the dependent variable, can further infer the conditional probability distribution of the dependent variable, effectively reflecting the impact of explanatory variables on the explained variable at different quantile points. In other words, quantile regression can detail the mapping information of input information on the response variable across different ranges. Its formula is

Where: Q_Y – the conditional quantile of the explained variable Y given the explanatory variable X, where X=[1, x₁, x₂, x₃, …, x_s]^T;

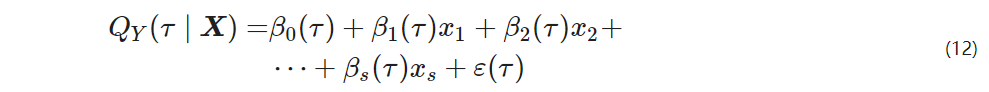
τ – quantile point, τ∈(0, 1);

β₀, β₁, β₂, …, β_s – components of the regression coefficient vector β(τ), β(τ)=[β₀, β₁, β₂, …, β_s]^T, whose values change with the quantile point τ;

ε(τ) – the error term at different quantile points τ.

2.2.2 LSTM Artificial Neural Network

Recurrent Neural Networks (RNN) can effectively process sequential data, but when RNN learns long sequences, problems of gradient explosion and vanishing gradients occur, making it difficult for RNN to grasp long-span nonlinear relationships. To address the long-term dependency problem of RNN, the concept of LSTM was proposed. Its main unit structure is shown in Figure 2. Figure 2 depicts a rectangular box known as an LSTM cell, consisting of an input gate i_t, output gate o_t, forget gate f_t, hidden state h_t, cell state c_t, and activation function σ. The input data for the LSTM neural network at time t is x_t, the output value is h_t, and the memory state is c_t, while c~tc~t represents the new candidate state.

From Figure 2, it can be seen that the values from the previous moment’s hidden layer h_t-1 and the current moment’s input value x_t are processed through the forget gate to discard invalid information, i.e.

The newly calculated information is then processed through a Sigmoid function to determine which information to update, obtaining the data to be input into the memory cell. The tanh layer creates a new candidate valuec~tc~t, which may be added to the cell state, i.e.

Then, the old state of the cell is updated to the current moment’s cell state value c_t, i.e.

Finally, the new cell state value c~tc~t processed through the tanh layer and the data classified by the Sigmoid function can be used to obtain the hidden layer data values passed to the next moment, i.e.

Where: w – weight matrix;

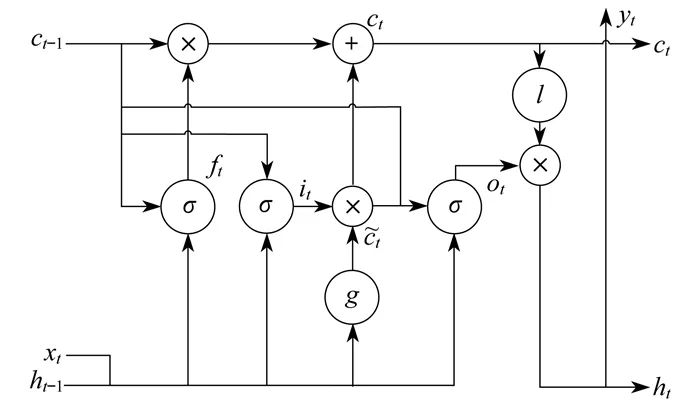
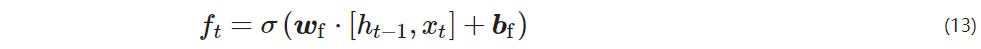
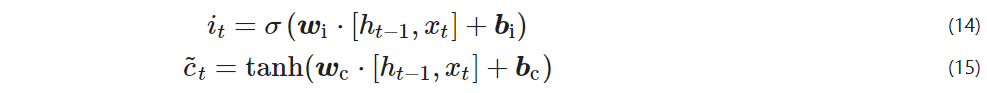
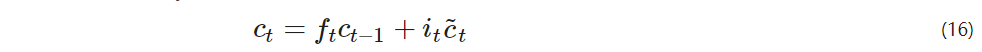
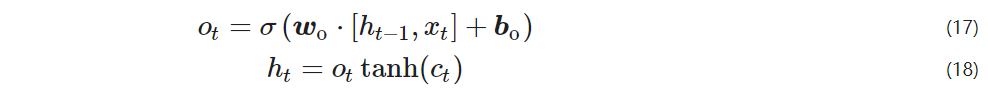
b – bias vector;

Subscripts f, i, c, o – corresponding items of the forget gate, input gate, memory cell, and output gate;

σ(·) – Sigmoid activation function;

tanh(·) – hyperbolic tangent activation function.

2.2.3 LSTM-Based Quantile Regression Model

To obtain a more accurate and narrower prediction interval for photovoltaic output, a quantile regression model based on neural networks is constructed in combination with the characteristics of the LSTM regression model. This model can ultimately treat parameter estimation as an optimization problem, solved using the Adam stochastic gradient descent method. The specific model is as follows

Where: f_cost – the objective function of quantile regression;

w~(t)w~(t), b~(t)b~(t) – the weight matrix and bias vector with quantile conditions.

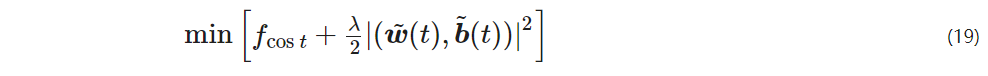
Assuming there are K neurons in the hidden layer of the LSTM network, the output vector of the hidden layer at time t is H_t¹, H_t², …, H_t^k. The hidden layer output vector is input into the fully connected layer to obtain the output value of the LSTM network at the quantile points as follows

Where: g(·) – linear activation function;

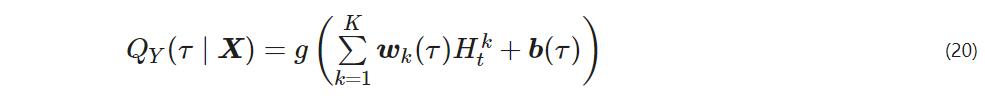
w_k(τ), b(τ) – the weight matrix and bias vector between the LSTM hidden layer output and the fully connected layer input.

2.3 Extreme Scenario Method

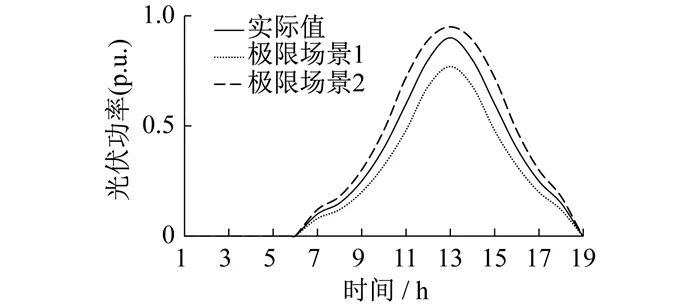
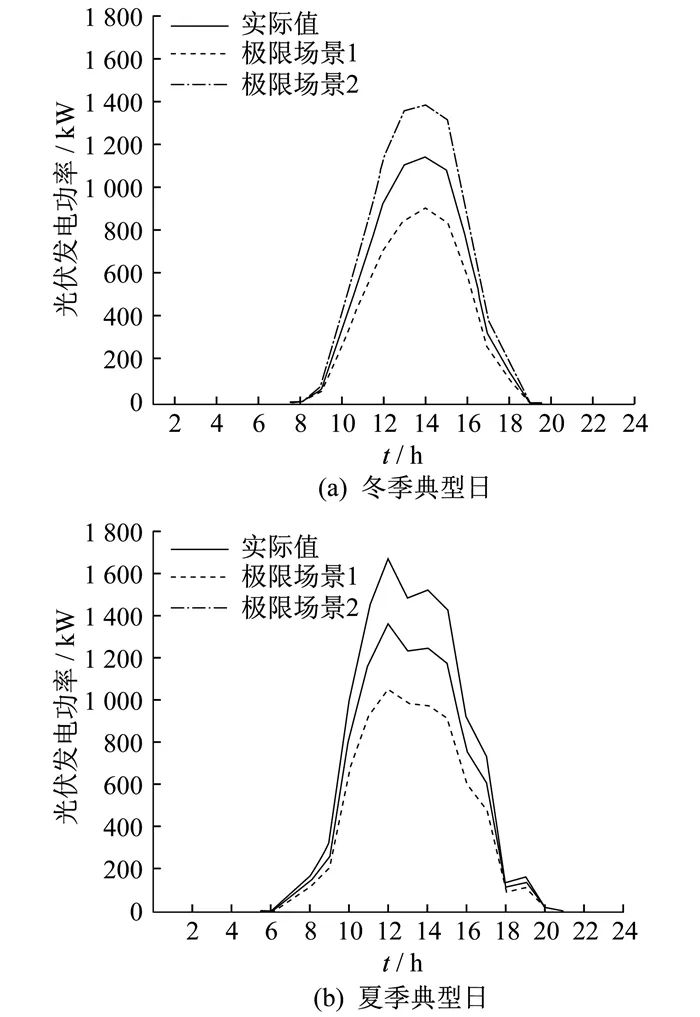
Based on the LSTM quantile regression model, a certain confidence level interval for photovoltaic power generation output can be predicted, further determining the extreme scenarios of photovoltaic power generation output at different confidence levels. When the confidence level is 0.9, taking F(P_l^PV) as 0.1 and F(P_u^PV) as 0.9, the fluctuation interval of photovoltaic power generation is [F(P_l^PV), F(P_u^PV)]. Therefore, setting the photovoltaic output power of extreme scenario 1 as F(P_l^PV) and the photovoltaic output power of extreme scenario 2 as F(P_u^PV). The actual value of photovoltaic power generation and extreme scenarios are shown in Figure 3.

3 Uncertainty Optimization Planning Model of Zero-Carbon Energy System

3.1 Objective Function

The total annual economic cost of the system W_total includes the annual average total investment cost of the equipment Z_total, the total annual maintenance cost of the equipment M_total, and the annual operating cost of the system U_total. The optimization planning objective of the zero-carbon energy system is to minimize the total annual economic cost W_total, which can be expressed as

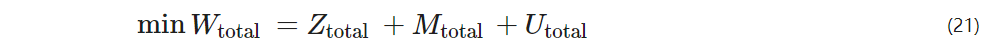
3.2 Constraints

3.2.1 Energy Balance Constraints

According to the differences in output from the energy supply equipment and user load forms, energy balance is reflected in electricity, heat, and cooling aspects, expressed as

Where: P_{t, l}^U, H_{t, l}^U, C_{t, l}^U – user electrical, thermal, and cooling load demands;

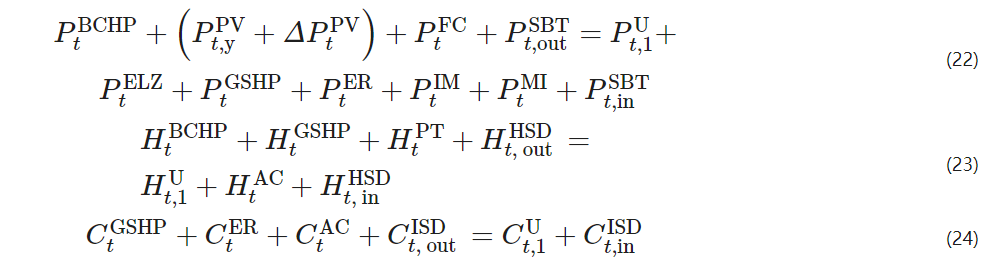
P_t^IM+P_t^MI – the electrical power consumed by ice storage air conditioning for ice making and melting;

P_{t, in}^SBT, P_{t, out}^SBT – the charging and discharging power of the battery at time t;

H_t^BCHP – the waste heat from the biomass CHP unit;

H_{t, in}^HSD, H_{t, out}^HSD – the stored and released heat amount from the thermal storage tank at time t.

3.2.2 Operational Constraints of Energy Supply Equipment

In the energy supply system, the output of power generation equipment, heating equipment, and cooling equipment must meet the upper and lower limits of their normal operating ranges, i.e.

Where: E_min^k, E_max^k – the minimum and maximum output values allowed for the kth device to operate normally;

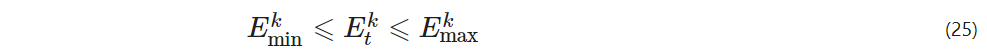
E_t^k – the output energy of the kth energy supply equipment at time t.

The area of photovoltaic panels is limited by actual site conditions and should meet the following constraint

Where: A^PV – the area occupied by photovoltaic panels;

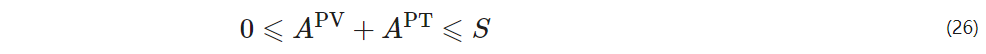
S – the maximum area allowed for photovoltaic panels and solar thermal equipment based on actual conditions.

The operational constraints for the electrolyzer are

Where: P_min^ELZ, P_max^ELZ – the idle power and rated power of the electrolyzer.

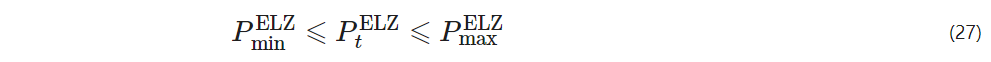
3.2.3 Operational Constraints of Energy Storage Equipment

Taking batteries as an example, the minimum energy capacity is defined to represent the threshold of remaining energy in the battery, and it is stipulated that the initial charge of the battery is zero, and the battery should not charge and discharge simultaneously. Its operational constraints can be expressed as

Where: β – coefficient, β∈(0, 1), which protects the battery;

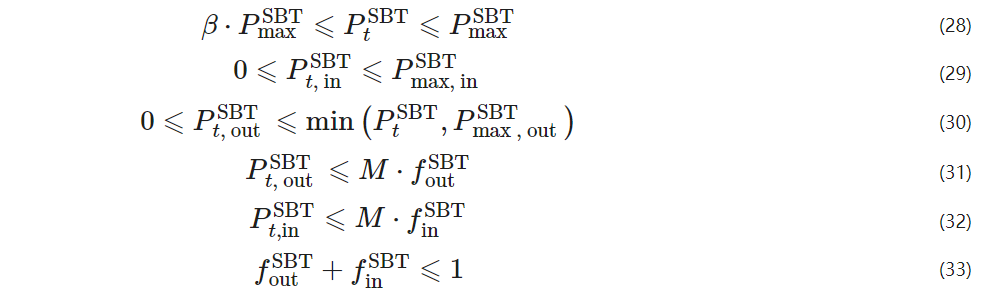
P_max^SBT – the rated capacity of the battery;

P_{max, in}^SBT, P_{max, out}^SBT – the maximum charging and discharging amounts allowed for the battery per unit time;

P_{t, in}^SBT, P_{t, out}^SBT – the charging and discharging amounts of the battery at time t;

M – maximum value;

f_in^SBT, f_out^SBT – the state values of battery charging and discharging, taking 0 or 1.

Since batteries cannot charge and discharge simultaneously, a maximum value M is introduced to limit their charging and discharging states.

4 Example Analysis

4.1 Example Parameters

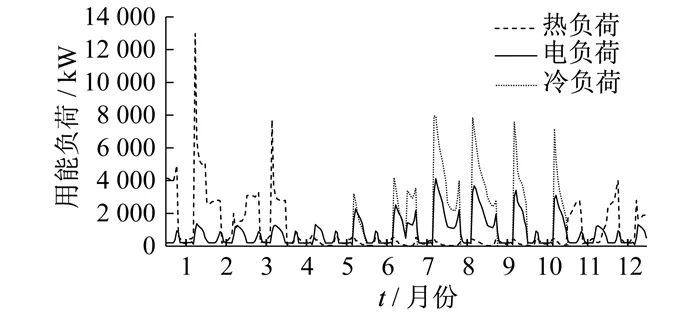
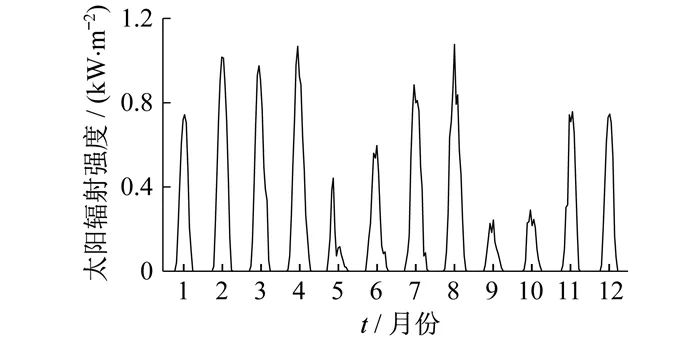
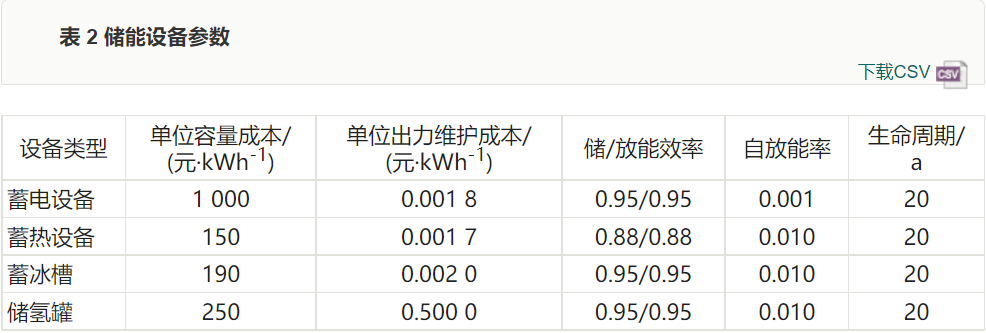
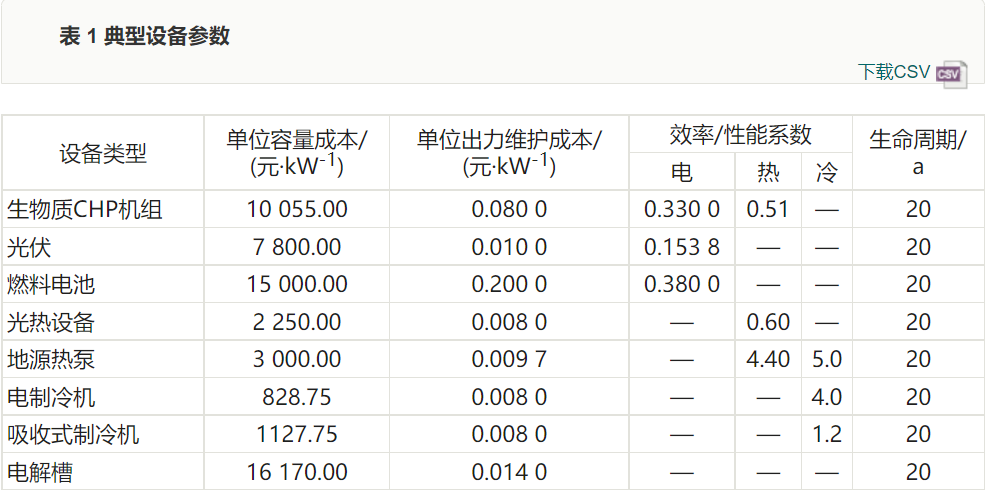
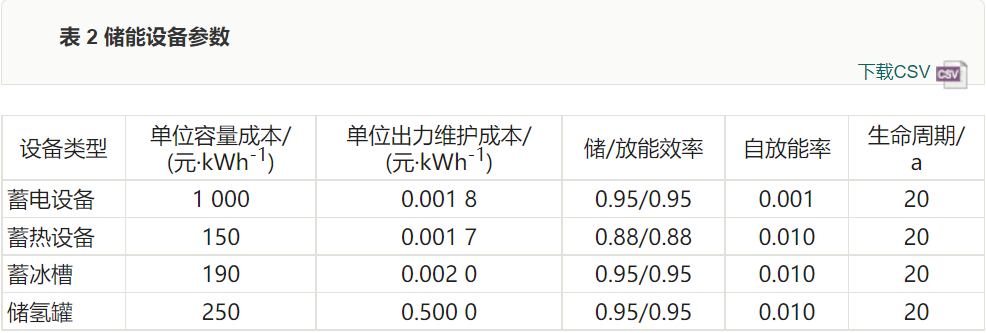
For a typical region, the 15th of each month is selected as a typical day, obtaining the user’s monthly electricity, heat, and cooling load demand curves, as shown in Figure 4. Figure 5 shows the corresponding hourly solar radiation intensity. The technical and economic parameters of the system supply and storage equipment are shown in Tables 1 and 2.

Based on the hourly photovoltaic generation output data throughout the year, data from 2,905 time points over the first four months are selected as training samples, using the LSTM quantile regression model to perform interval predictions for photovoltaic power generation on typical days. Among them, the interval prediction results for photovoltaic power generation during typical winter and summer days are shown in Figure 6.

4.2 Analysis of Optimization Planning Results

4.2.1 Analysis of Equipment Capacity Optimization Results

To analyze the impact of photovoltaic output uncertainty on the operation of the zero-carbon energy system, two scenarios are set for comparison: scenario 1 and scenario 2, which respectively consider and do not consider photovoltaic output uncertainty.

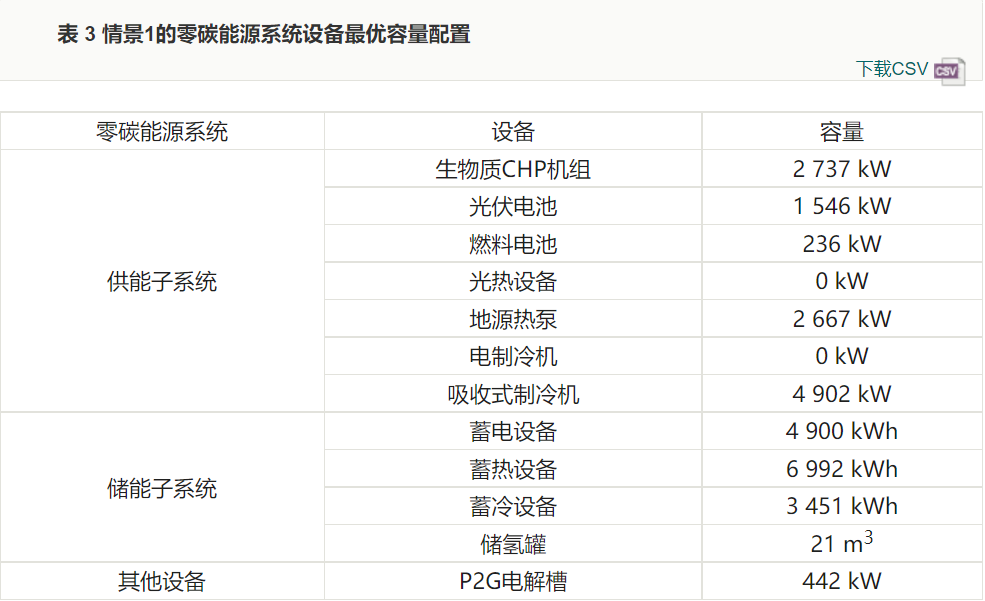
Table 3 shows the system’s optimal capacity configuration determined in scenario 1. Compared to the physical structure of the energy system constructed in Figure 1, both electric chillers and solar thermal equipment were not selected. This is mainly because the capacity of the biomass CHP unit is relatively large, and the waste heat from the unit can fully supply the cooling load through the absorption chiller. The user’s annual thermal load demand is fixed, and the biomass CHP unit and ground source heat pump are stable heating equipment. Meanwhile, due to certain limitations on the planning area of photovoltaic and solar thermal equipment, the benefits of solar energy generation far exceed those of solar thermal generation, thus solar thermal equipment was also not selected.

In scenario 2, the equipment configurations under two extreme scenarios are shown in Table 4. Compared to the system capacity configuration in scenario 1, due to the decrease in photovoltaic power output, the photovoltaic capacity in scenario 2 is correspondingly reduced. To further balance the user’s electrical load demand, the capacity of the biomass CHP unit is increased; however, the capacity of the fuel cell remains unchanged due to its high unit capacity investment cost and output cost. The increase in the capacity of the biomass CHP unit indirectly leads to an increase in the waste heat from biomass, thereby reducing the system’s reliance on the thermal output of the ground source heat pump, which results in a decrease in the capacity of the ground source heat pump and an increase in the capacity of the absorption chiller. In extreme scenario 1, the capacity of energy storage equipment only changes slightly, but in extreme scenario 2, the capacities of battery, thermal storage, and cooling storage equipment all increase to varying degrees. This is mainly due to the increase in photovoltaic power output, which raises the capacity of battery equipment to enhance the utilization of renewable energy and mitigate the volatility of photovoltaic power generation.

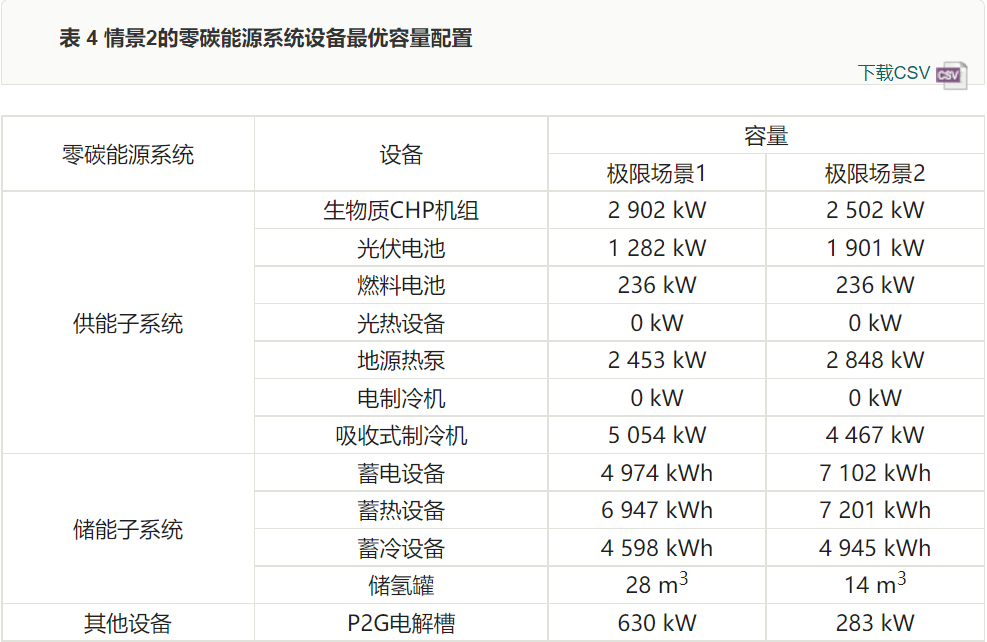
4.2.2 Economic Analysis of the System

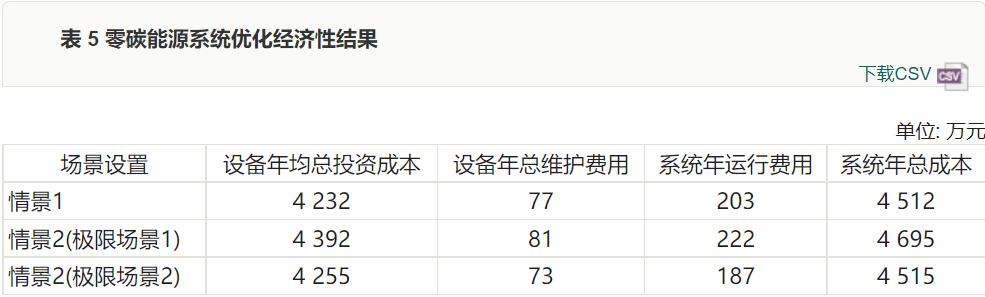
To clarify the advantages and disadvantages of system configuration schemes under different scenarios, a comparative analysis of the economic performance of the systems in scenario 1 and the two extreme scenarios in scenario 2 is conducted, with results shown in Table 5. As can be seen from Table 5, considering uncertainty leads to an increase in the total cost of the system.

4.2.3 Energy Balance Analysis

To further understand the impact of renewable energy uncertainty on the operation scheduling of the zero-carbon energy system, the operational strategies of equipment output during typical summer days in extreme scenarios 1 and 2 are compared, with results shown in Figures 7 and 8.

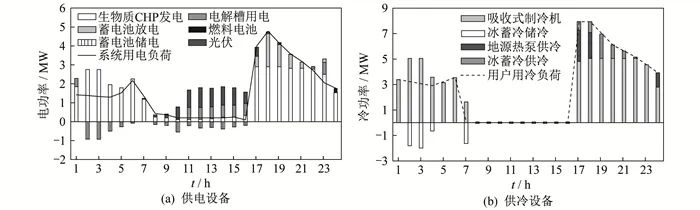
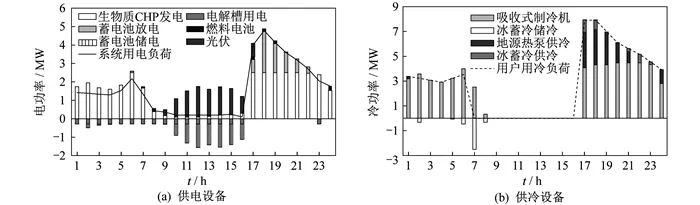
In extreme scenario 1, during the day, the excess photovoltaic power generation output meets the user’s electrical load demand, and the surplus electricity is partially stored in the battery and partially used to electrolyze water to produce hydrogen, stored in hydrogen tanks. However, in extreme scenario 2, the excess photovoltaic power generation output is predominantly stored in the battery, primarily because the battery equipment capacity is large, and directly storing in the battery is more economically viable. In both scenarios, the biomass CHP unit’s power generation is the main source of electricity for the system. At night, when the photovoltaic panels generate no power, if the power generation from the biomass CHP unit and the battery discharge cannot meet the user’s electrical load demand, the system will activate the fuel cell for power generation. The frequent activation of the fuel cell reduces the economic viability of the system, which explains why the system’s economic costs in both extreme scenarios of scenario 2 are higher than those in scenario 1. In both extreme scenarios, the user’s cooling load demand is primarily met by the absorption chiller, while the ground source heat pump serves as an auxiliary cooling device, and the ice storage equipment stores excess cooling during peak cooling periods and releases it at night.

5 Conclusion

Considering the volatility and intermittence of renewable energy such as photovoltaic in zero-carbon energy systems, this paper establishes an uncertainty optimization planning model based on LSTM quantile regression using interval number theory. Through typical case analysis, it is concluded that under current technological and economic conditions, for the small distributed zero-carbon energy systems discussed in this paper, photovoltaic generation is an essential element, and biomass CHP generation, benefiting from its controllable output characteristics, will also play an important role; the consideration of renewable energy output uncertainty will significantly impact system configuration, necessitating the consideration of the worst-case scenarios during actual planning; the consideration of uncertainty will affect equipment investment costs, operational maintenance costs, etc., ultimately leading to an increase in total system costs, but the increase is limited.

References

• [1]Sun Rongfu, Zhang Tao, He Qing, et al. Review of Key Technologies and Applications for Wind Power Prediction[J]. High Voltage Technology, 2021, 47(4): 1129-1143.

• [2]Li Jinghua, Zhu Mengshu, Lu Yuejiang, et al. Review of Integrated Energy System Optimization Scheduling[J]. Power System Technology, 2021, 45(6): 2256-2272.

• [3]Zhou Yutong, Hua Liangliang, Huang Wei, et al. Regional Integrated Energy Multi-objective Optimization Configuration Considering Electric and Thermal Trading[J]. Modern Electric Power, 2019, 36(4): 24-30.

• [4]Zhang Ziyang, Zhang Niepeng, Wang Manshang, et al. Research on Optimization Planning Model of Integrated Energy System for High Proportion of Renewable Energy Consumption[J]. Renewable Energy, 2020, 38(8): 1085-1091.

• [5]Ma Yiwei, Yang Ping, Wu Jie, et al. Optimization Design of Island-type Hybrid Renewable Energy Power Generation Systems[J]. Journal of South China University of Technology (Natural Science Edition), 2012, 40(11): 113-120.

• [6]Li Jinze, Liu Pei, Li Zheng. Modeling and Optimization of Off-grid Hybrid Renewable Energy Systems in Remote Areas[J]. Journal of Engineering Thermophysics, 2021, 42(5): 1113-1118.

• [7]Kai Saijiang, Ji Li, Zhou Zhuan, et al. Capacity Optimization Configuration of 100% Renewable Energy Integrated Energy System[J]. Distributed Energy, 2021, 6(4): 34-40.

• [8]Jia Yunhui, Zhang Feng. Research on Multi-layer Optimization Configuration of Regional Integrated Energy System Considering Distributed Wind Power Access[J]. Renewable Energy, 2019, 37(10): 1524-1532.

• [9]Jiang Enyu, Ji Liang, Xia Nenghong, et al. Photovoltaic Power Generation Prediction Based on Support Vector Machine[J]. Journal of Shanghai Electric Power Institute, 2015, 31(6): 511-513.

• [10]Cui Chenggang, Zou Yuhang. LSTM Photovoltaic Prediction Based on Deep Learning[J]. Journal of Shanghai Electric Power Institute, 2019, 35(6): 544-552.

• [11]Li Fen, Qian Jialin, Yang Xingwu, et al. Short-term Photovoltaic Power Generation Prediction Based on CAR Model[J]. Journal of Shanghai Electric Power Institute, 2015, 31(6): 514-518.

• [12]Li Meicheng, Mei Wenming, Zhang Lingkang, et al. Research on Multi-energy Microgrid Scheduling Optimization Model Considering Renewable Energy Uncertainty[J]. Power System Technology, 2019, 43(4): 1260-1270.

• [13]Lv Haipeng, Xiwang Abuduwaiti, Meng Lingpeng. Microgrid Two-level Stochastic Optimization Scheduling Considering Source-load Forecasting Uncertainty[J]. Power Automation Equipment, 2022, 42(9): 70-78.

• [14]Bai Muke, Wang Yue, Tang Wei, et al. Day-ahead Economic Optimization Scheduling of Regional Integrated Energy Systems Based on Interval Linear Programming[J]. Power System Technology, 2017, 41(12): 3963-3970.

• [15]Qiu Zhi, Wang Beibei, Ben Shujun, et al. Bi-level Optimization Configuration Planning Model of Regional Integrated Energy System Considering Uncertainty[J]. Power Automation Equipment, 2019, 39(8): 176-185.

• [16]Liuping, Yang Weihua, Zhang Jian, et al. Research Progress on Emission Reduction Technologies Under Carbon Neutral Goals[J]. Modern Chemical Industry, 2021, 41(6): 6-10.

• [17]CHAUHAN A, SAINI R P. Discrete harmony search based size optimization of integrated renewable energy system for remote rural areas of Uttarakhand state in India[J]. Renewable Energy, 2016, 94: 587-604.

• [18]Li Weikang, Wang Dan, Yu Xiaodan, et al. Multi-objective Planning of Micro Energy Networks Considering Electrical Conversion Storage and Renewable Energy Integration[J]. Power System Automation, 2018, 42(16): 11-20.

• [19]XU Wenxiu. Research on Topic Classification in Renewable Energy Field Based on LSTM and LDA[D]. Jinan: Shandong University, 2020.

• [20]TAYLOR J W. A quantile regression neural network approach to estimating the conditional density of multiperiod returns[J]. Journal of Forecasting, 2000, 19(4): 299-311.

• [21]Huang Shengquan. Short-term Power Load Prediction Based on Deep Learning[D]. Guangzhou: Guangdong University of Technology, 2019.

• [22]Hou Hui, Liu Peng, Huang Liang, et al. Planning of Power-Heat-Hydrogen Integrated Energy System Considering Uncertainty[J]. Transactions of China Electrotechnical Society, 2021, 36(Supplement 1): 133-144.

• [23]Zhou Canhuang, Zheng Jiehui, Jing Zhaoxia, et al. Multi-objective Optimization Design of Integrated Energy Systems for Park Microgrids[J]. Power System Technology, 2018, 42(6): 1687-1697.

• [24]LI J R, LIN J, ZHANG H C, et al. Optimal investment of electrolyzers and seasonal storages in hydrogen supply chains incorporated with renewable electric networks[J]. IEEE Transactions on Sustainable Energy, 2019, 11(3): 1773-1784.

Scan to Follow Us

E-MAIL: [email protected]

Website: http://shdlxyxb.ijournals.cn