Machine learning can be approximately equated to finding a functional function f related to specific inputs and expected outputs through statistical or inferential methods within data objects (as shown in Figure 1). Usually, we denote the input variable (feature) space as uppercase X and the output variable space as uppercase Y. Therefore, machine learning can be approximately expressed as Y≈f(X).
Figure 1: Machine learning is approximately finding a useful function
In such a function, for speech recognition, if an audio signal is input, this function f can output recognition information such as “你好” or “How are you?” For image recognition, if an image is input, this function can output (or recognize) a judgment of either a cat or a dog. For chess game functions, if a Go game situation is input, it can output the “best” move for that game. For intelligent interactive systems (like Microsoft’s Xiaoice), when we input a statement like “How are you?” into this function, it can output an intelligent response such as “I am fine, thank you.” Each specific input is an instance, typically composed of a feature vector. Here, the space where all feature vectors exist is called the feature space, with each dimension of the feature space corresponding to one feature of the instance. However, the problem arises that such a “useful” function is not easy to find. After inputting a picture of a cat, this function may not necessarily output “this is a cat”; it might incorrectly output “this is a dog” or “this is a snake.” Thus, we need to build an evaluation system to discern the quality of the function. Of course, this requires training data to “cultivate” the good qualities of the function. As mentioned earlier, the core of learning is to improve performance. Figure 2 illustrates the three steps of machine learning; through training data, we improve f1 to f2, where even though f2 still contains classification errors, its performance (classification accuracy) is improved compared to the complete errors of f1, which is learning.
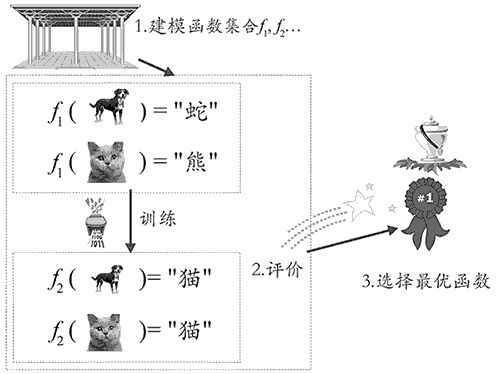Figure 2: The Three Steps of Machine Learning
Specifically, to excel in machine learning, we need to accomplish three major steps:
-
How to find a series of functions to achieve the expected functionality, which is a modeling problem;
-
How to find a series of evaluation criteria to assess the quality of the function, which is an evaluation problem;
-
How to quickly find the function with optimal performance, which is an optimization problem.
Conventionally, we represent specific input variables and output variables with lowercase x and y. Variables can be either scalar or vector. Unless otherwise specified, the vectors referred to in this tutorial are column vectors. The standard notation is shown in Figure 3(a), but this notation takes up more space, so we usually adopt the transposed notation, as shown in Figure 3(b), where the superscript “T” denotes the transpose symbol.
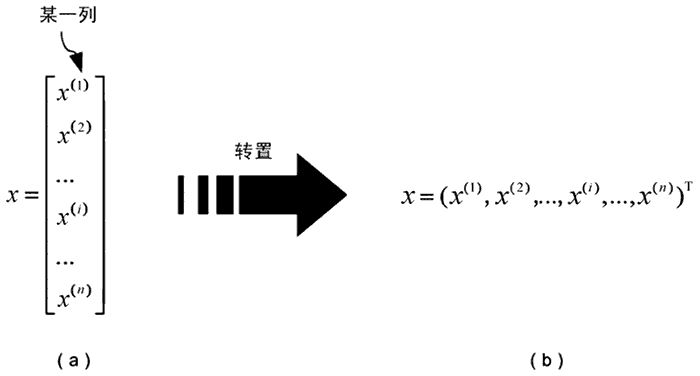Figure 3: Feature Vector Matrix
Here, x(i) represents the i-th feature of the input variable x. It is important to note that when there are multiple input variables, we use xj to denote them. Thus, xj(i) indicates the i-th feature of the j-th variable, as shown in the feature vector matrix in Figure 4.
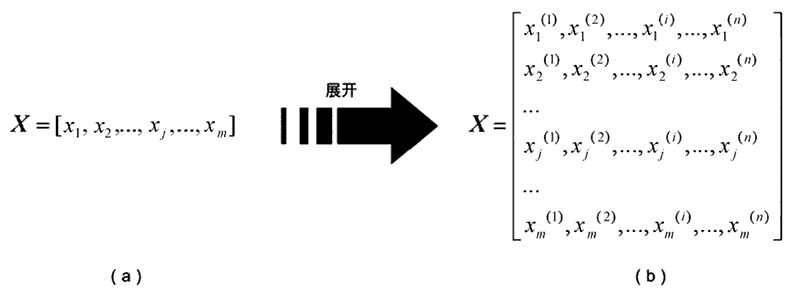Figure 4: Feature Vector Matrix
For supervised learning, the constructed model typically learns from the training data set, adjusting model parameters, and then validating predictions in the test data set. For training data, the input signals (or variables) and output signals (or variables) usually appear in pairs. Sometimes, the output signal is referred to as the “teacher signal” because it provides guidance and can “train” the parameters in the model through a loss function. Therefore, the training data set is typically described in the following way:
T ={(x1, y1),(x2, y2),…,(xj, yj),…(xm, ym)}
Input variables and output variables can have different types; they can be continuous or discrete. Generally, people assign different names to prediction tasks based on the types of input and output variables. For example, if both input and output variables are continuous, the prediction task is called regression. If the output variable is a finite discrete value, the prediction task is called classification. If both input and output variables are sequences of variables, the prediction task is called tagging, which can be considered an extension of classification.