Excerpt from Sebastian Ruder Blog
Author: Sebastian Ruder
Translated by: Machine Heart
Contributors: Terrence L
This article is Part 3 of the Word Embedding Series, introducing the popular word embedding model Global Vectors (GloVe). To read Part 2, click on Technical | Word Embedding Series Part 2: Comparing Several Methods of Approximate Softmax in Language Modeling; for Part 1, click on Technical | Word Embedding Series Part 1: Word Embedding Models Based on Language Modeling.
-
Global Vectors (GloVe)
-
Word Embedding and Distributed Semantic Models
-
Models
-
Hyperparameters
-
Results
Please forgive the previous hype. This is a blog I have wanted to write for a long time. In this article, I want to highlight the secret ingredients that made word2vec successful.
I will specifically focus on the connection between word embeddings trained via neural models and those generated by traditional Distributed Semantic Models (DSMs). By demonstrating how these components are transferred to DSMs, I will show that distributed methods are as good as popular word embedding methods.
While there are no new insights, I feel that traditional methods are often overshadowed by the wave of deep learning, and their relevance should receive more attention.
Therefore, the literature this blog is based on is the research by Levy et al. published in 2015, which improves distributed similarity through word embeddings. If you haven’t read it yet, I recommend you search for it.
In this public blog, I will first introduce a popular word embedding model, GloVe, and then highlight the connection between word embedding models and distributed semantic methods.
Next, I will introduce four models used to measure the impact of different factors. After that, I will provide an overview of additional factors in learning word representations, aside from algorithm choice. Finally, I will present Levy et al.’s suggestions and conclusions.
Global Vectors (GloVe)
In the previously published blog, we overviewed popular word embedding models. One model we missed is GloVe.
In short, GloVe aims to clarify the implicit operations of SNGS: encoding meaning as vector shifts in the embedding space — which appears to be a mere byproduct of word2vec — is the specific goal of GloVe.
Specifically, the authors of GloVe indicate that the ratio of co-occurrence probabilities of two words (rather than their co-occurrence probabilities themselves) contains information and is intended to encode information as vector differences.
To achieve this, they propose an objective J using weighted least squares aimed at minimizing the difference between the dot product of two words’ vectors and the logarithm of their co-occurrence counts.
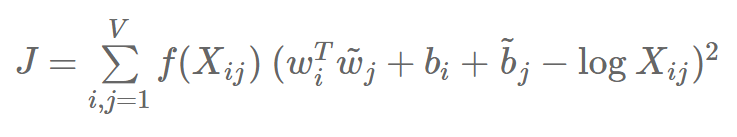where wi and bi are the word vector and bias for word i, w~j and bj are the text word vector and bias for word j, Xij is the count of how many times word i appears in the text of word j, and f is a weighting function that assigns relatively low weights to rare and frequent co-occurrences.
Co-occurrence counts can be directly encoded into the co-occurrence matrix of word contexts, and GloVe will use such a matrix instead of the entire corpus as input.
If you want to learn more about GloVe, the best reference is the related paper or its affiliated website
(http://nlp.stanford.edu/projects/glove/). Besides, you can gain more insights into GloVe and its differences from word2vec through the authors of Gensim, Quora Q&A (https://www.quora.com/How-is-GloVe-different-from-word2vec), or this published blog
(https://cran.r-project.org/web/packages/text2vec/vignettes/glove.html).
Word Embedding and Distributed Semantic Models
The reason why word embedding models, especially word2vec and GloVe, have become so popular is that their performance seems to consistently outperform DSMs. Many attribute this to the neural architecture of Word2Vec or the fact that it can predict words, which appears to have a natural advantage over mere co-occurrence counts.
We can think of DSMs as counting models, as they calculate the co-occurrence counts of words by operating on co-occurrence matrices. In contrast, neural word embedding models can be viewed as predictive models because they predict surrounding words.
In 2014, Baroni et al. demonstrated that predictive models outperformed counting models in almost all tasks, providing clear evidence for the apparent superiority of word embedding models. Is this the end point? No.
We have seen that the differences with GloVe are not so obvious: when GloVe is considered a predictive model by Levy et al., it is clearly decomposing a word context co-occurrence matrix, bringing it closer to traditional methods like Principal Component Analysis (PCA) and Latent Semantic Analysis (LSA). Moreover, Levy et al. also indicated that word2vec implicitly decomposes the PMI matrix of word contexts.
Therefore, although DSMs and word embedding models use different algorithms to learn word representations — the former counts, and the latter predicts — fundamentally, both types of models reflect the same underlying statistical data, namely the co-occurrence counts between words.
Thus, there remains a question that this blog aims to address:
Why do word embedding models still perform better than DSMs, which have nearly the same information?
Models
Continuing from Levy et al.’s 2015 findings, we will separate and identify the factors affecting neural word embedding models and demonstrate how they are transferred to traditional methods by comparing the following four models:
-
PPMI: PMI is a commonly used metric to measure the strength of correlation between two words. It is the logarithmic ratio of the joint probability of two words w and c to the product of their marginal probabilities:
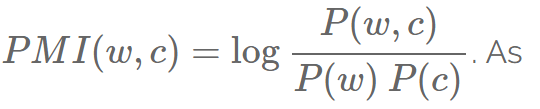
PMI(w,c)=logP(w,c)P(w)P(c). Since the PMI(w,c)=log0=−∞ for word pairs (w,c) that never occur,
PMI is often replaced by PPMI, which treats negative values as 0, i.e.: PPMI(w,c)=max(PMI(w,c),0)
-
Singular Value Decomposition (SVD): SVD is one of the most popular dimensionality reduction methods, which was originally introduced into Natural Language Processing (NLP) through Latent Semantic Analysis (LSA). SVD transforms the word-text co-occurrence matrix into a three-way matrix.
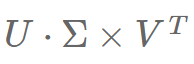
where U and V are orthogonal matrices (i.e., the rows and columns of a square matrix are orthogonal unit vectors), and Σ is a diagonal matrix of eigenvalues during the weakening process. In practice, SVD is often used to factorize the matrix produced by PPMI. Generally, only the top d elements of Σ are retained, resulting in:
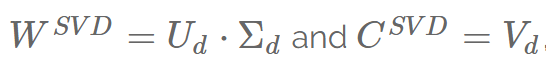
which are generally used to represent words and contexts.
-
Skip-gram Model Based on Negative Sampling, which is word2vec: For more on the skip-gram structure and negative sampling, refer to my previous blog post.
-
Global Vectors (GloVe): Already introduced in the previous section.
Hyperparameters
Let’s take a look at the following hyperparameters:
-
Preprocessing
-
Dynamic Context Window
-
Common Word Downsampling
-
Removing Rare Words
-
Association Measures
-
Transfer
-
Context Distribution Smoothing
-
Post-processing
-
Adding Context Vectors
-
Eigenvalue Weighting
-
Vector Normalization
Preprocessing
Word2vec introduces three methods for preprocessing the corpus, which can also be easily applied to DSM.
Dynamic Context Window
Generally, in DSM, context windows are not weighted and have a constant size. However, SGNS and GloVe use a scheme that assigns more weight to closer words, as closer words are often considered more important to the meaning of the word. Additionally, in SGNS, the window size is not fixed; instead, the actual window size is dynamic and is uniformly sampled between 1 and the maximum window during training.
Common Word Downsampling
SGNS randomly removes words with frequency f above a certain threshold t using the probability:
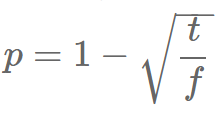
to obtain those very frequently occurring words. Since this downsampling is done before the actual creation of the window, the context window used in practice is larger than the actual indicated context window.
Removing Rare Words
In the preprocessing of SGNS, rare words are also removed before creating the context window, further increasing the actual size of the context window. Although Levy et al. found in 2015 that this does not have a significant impact on performance.
Association Measures
PMI has been shown to be an effective way to measure the degree of association between words. Levy and Goldberg indicated in 2014 that SGNS implicitly factorizes the PMI matrix, thus allowing two variations of this formula to be introduced into conventional PMI.
PMI Transfer
In SGNS, the larger the number of negative samples K, the more data is used, and the better the parameter estimates. K affects the shift of the PMI matrix implicitly factorized by word2vec, i.e., k shifts the PMI value by log k.
If we convert it to conventional PMI, we obtain Shifted PPMI: SPPMI(w,c)=max(PMI(w,c)−logk,0).
Context Distribution Smoothing
In SGNS, negative samples are sampled according to a smoothed univariate distribution, specifically by raising the univariate distribution to the power of α, which is empirically set to 34. This results in frequent words being sampled less than their frequency would suggest.
We can transfer the frequency of the context vocabulary f(c) equally raised to the power of α to PMI:
PMI(w,c)=log p(w,c)p(w)pα(c) where pα(c)=f(c)αΣcf(c)α and f(x) is the frequency of word x.
Post-processing
Similar to preprocessing, three methods can be used to modify the word vectors generated by the algorithm.
Adding Context Vectors
The authors of GloVe suggest adding word embeddings and context vectors to create the final output vector, e.g.: v⃗cat =w⃗cat +c⃗catv→cat = w→cat + c→cat. This increases the first-order similarity term, i.e., w⋅v. However, this method cannot be applied to PMI since PMI generates sparse vectors.
Eigenvalue Weighting
SVD produces the following matrices: WSVD = Ud·Σd and CSVD = Vd. However, these matrices have different properties: CSVD is standard orthogonal, while WSVD is not.
In contrast, SGNS is more symmetric. Therefore, we can use an adjustable additional parameter pp to weight the eigenvalue matrix Σd to produce the following:
WSVD = Ud·Σpd.
Vector Normalization
Finally, we can also normalize all vectors to unit length.
Results
In 2015, Levy et al. trained models on all dumps of English Wikipedia and evaluated them based on similarities and analogy datasets of common words. You can find more information about the experimental setup and training details in their paper. Below, we summarize the most important results and takeaways.
Additional Takeaways
Levy et al. found that SVD — rather than one of the word embedding algorithms — performs best on similarity tasks, while SGNS excels on analogy datasets. They also clarified the importance of hyperparameters compared to other choices:
1. Hyperparameters vs. Algorithms: Hyperparameter settings are often more important than algorithm choice. There is no single algorithm that always outperforms others.
2. Hyperparameters vs. More Data: Training on larger corpora helps for certain tasks. In 3 out of 6 examples, tuning hyperparameters is more beneficial.
Revealing Previous Views
With these insights, we can now reveal some commonly held views:
-
Are embeddings superior to distributed methods? With the right hyperparameters, neither method has a lasting advantage over the other.
-
Is GloVe superior to SGNS? SNGS outperforms GloVe in all tasks.
-
Is CBOW a good configuration for word2vec? CBOW does not outperform SGNS on any task.
Recommendations
Lastly — and this is my favorite part of this article — we can provide some specific practical recommendations:
-
Do not use transferred PPMI with SVD.
-
Do not “correctly” use SVD, i.e., do not use eigenvector weighting (performance drops by 15 points compared to using p = 0.5 for eigenvalue weighting).
-
Please use PPMI and SVD with short contexts (window size of 22).
-
Please use many negative samples of SGNS.
-
For all methods, always use context distribution smoothing (raising the univariate distribution to the power of α = 0.75).
-
Use SGNS as a benchmark (training is more robust, fast, and economical).
-
Please try adding context vectors in SGNS and GloVe.
Conclusion
These results contradict the commonly assumed case that word embeddings outperform traditional methods and indicate that there is often no difference, whether using word embeddings or distributed methods — what matters is that you tune hyperparameters and use appropriate preprocessing and post-processing steps.
The latest paper from the Jurafsky group [5, 6] responds to these findings and indicates that SVD — rather than SGNS — is usually the preferred choice when you care about precise word representations.
I hope this blog helps the current focus on revealing the connections between traditional distributional semantics and embedding models. As we have seen, knowledge of distributed semantics allows us to improve current methods and develop new variants of existing methods. To this end, I hope that next time you train word embeddings, you will consider incorporating distributed methods or benefit from these reflections.
References:
Levy, O., Goldberg, Y., & Dagan, I. (2015). Improving Distributional Similarity with Lessons Learned from Word Embeddings. Transactions of the Association for Computational Linguistics, 3, 211–225. Retrieved from https://tacl2013.cs.columbia.edu/ojs/index.php/tacl/article/view/570 ↩
Pennington, J., Socher, R., & Manning, C. D. (2014). Glove: Global Vectors for Word Representation. Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing, 1532–1543. http://doi.org/10.3115/v1/D14-1162
Baroni, M., Dinu, G., & Kruszewski, G. (2014). Don’t count, predict! A systematic comparison of context-counting vs. context-predicting semantic vectors. ACL, 238–247. http://doi.org/10.3115/v1/P14-1023
Levy, O., & Goldberg, Y. (2014). Neural Word Embedding as Implicit Matrix Factorization. Advances in Neural Information Processing Systems (NIPS), 2177–2185. Retrieved from http://papers.nips.cc/paper/5477-neural-word-embedding-as-implicit-matrix-factorization
Hamilton, W. L., Clark, K., Leskovec, J., & Jurafsky, D. (2016). Inducing Domain-Specific Sentiment Lexicons from Unlabeled Corpora. Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics. Retrieved from http://arxiv.org/abs/1606.02820
Hamilton, W. L., Leskovec, J., & Jurafsky, D. (2016). Diachronic Word Embeddings Reveal Statistical Laws of Semantic Change. arXiv Preprint arXiv:1605.09096.
© This article is translated by Machine Heart, please contact this public account for authorization..
✄————————————————
Join Machine Heart (Full-time Reporter/Intern): [email protected]
Submissions or Seeking Coverage: [email protected]
Advertising & Business Cooperation: [email protected]
