Source: Mathematics China
This article is about 2200 words long and suggests a reading time of 9 minutes.
When there is an appropriate neural network architecture and a sufficiently large dataset, deep learning networks can learn any mapping from one vector space to another.
According to reports, the use of deep learning has rapidly increased over the past decade due to the adoption of cloud-based technologies and the use of deep learning systems in big data, with the market size expected to reach $93 billion by 2028.
But what exactly is deep learning, and how does it work?
Deep learning is a subset of machine learning that uses neural networks to perform learning and predictions. Deep learning has demonstrated remarkable performance across various tasks, whether in text, time series, or computer vision. The success of deep learning primarily comes from the availability of big data and computational power. However, this alone makes deep learning far superior to any classical machine learning algorithms.
Deep Learning: Neural Networks and Functions
A neural network is a network of interconnected neurons, each of which is a finite function approximator. Thus, neural networks are viewed as universal function approximators. If you remember high school math, a function is a mapping from an input space to an output space. A simple sin(x) function maps from the angular space (-180° to 180° or 0° to 360°) to the real number space (-1 to 1).
Let’s see why neural networks are considered universal function approximators. Each neuron learns a finite function: f(.) = g(W*X) where W is the weight vector to be learned, X is the input vector, and g(.) is a nonlinear transformation. W*X can be visualized as a line (learning) in high-dimensional space (hyperplane), and g(.) can be any nonlinear differentiable function, such as sigmoid, tanh, ReLU, etc. (commonly used in deep learning). Learning in a neural network is ultimately about finding the optimal weight vector W. For example, in y = mx+c, we have 2 weights: m and c. Now, based on the distribution of points in 2D space, we find the best values for m & c that satisfy certain criteria: minimizing the difference between predicted y and actual points for all data points.
The Effect of Layers
Now that each neuron is a nonlinear function, we stack several such neurons in a “layer”, where each neuron receives the same set of inputs but learns different weights W. Thus, each layer has a set of learning functions: [f1, f2, …, fn], known as hidden layer values. These values are again combined in the next layer: h(f1, f2, …, fn), and so on. This way, each layer consists of functions from the previous layer (similar to h(f(g(x)))). It has been shown that through this combination, we can learn any nonlinear composite function.
Deep learning involves neural networks with many hidden layers (usually > 2 hidden layers). But in reality, deep learning is a complex combination of functions from layer to layer, thereby finding the function that defines the mapping from input to output. For example, if the input is an image of a lion, the output is the classification of the image as belonging to the lion class. Similarly, if the input is a sequence of words, the output is whether the input sentence has a positive/neutral/negative sentiment. Thus, deep learning is learning the mapping from input text to output class: neutral or positive or negative.
Deep Learning as Interpolation
From a biological perspective, humans process images of the world layer by layer, from low-level features like edges and contours to high-level features like objects and scenes. The function combinations in neural networks align with this, where each function combination learns complex features about the image. The most common neural network architecture used for images is the Convolutional Neural Network (CNN), which learns these features in a hierarchical manner, followed by a fully connected neural network that classifies the image features into different categories.
Using high school math again, given a set of 2D data points, we attempt to fit a curve through interpolation that somewhat represents the function defining these data points. The more complex the function we fit (for example, determined by the degree of the polynomial in interpolation), the better it fits the data; however, it generalizes less well to new data points. This is where deep learning faces challenges, commonly known as the overfitting problem: fitting the data as much as possible while compromising on generalization. Almost all deep learning architectures must deal with this important factor to learn a general function that performs equally well on unseen data.
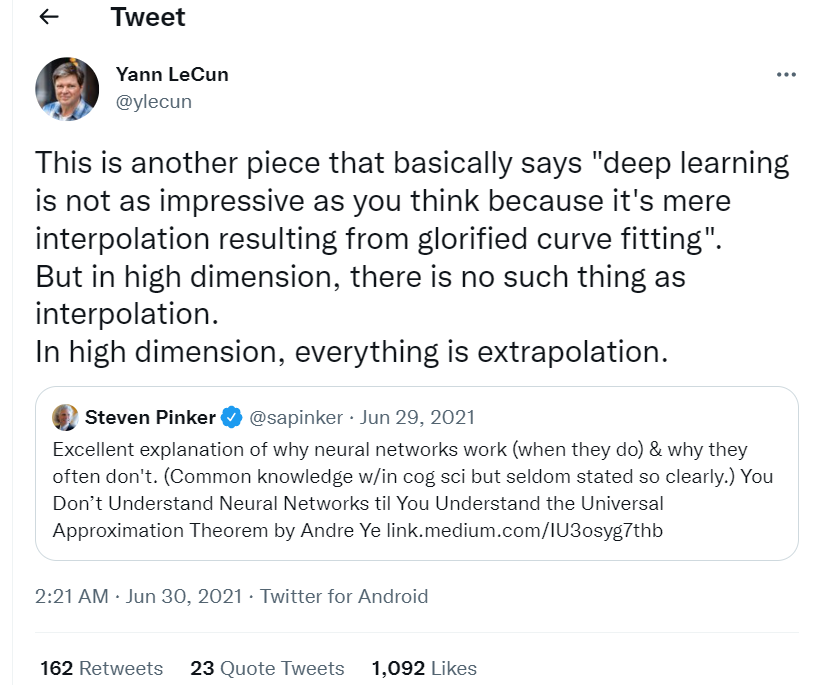
Pioneer of deep learning Yann LeCun (creator of Convolutional Neural Networks and ACM Turing Award winner) tweeted (based on a paper): “Deep learning is not as impressive as you might think because it is merely a beautified version of curve fitting interpolation. But in high dimensions, there is no such thing as interpolation. In high-dimensional space, everything is extrapolation.” Therefore, as part of function learning, deep learning involves not just interpolation, but in some cases, extrapolation. And that’s it!
Twitter Address: https://twitter.com/ylecun/status/1409940043951742981?lang=en
Learning Aspects
So, how do we learn this complex function? It entirely depends on the problem at hand, which determines the neural network architecture. If we are interested in image classification, we use CNNs. If we are interested in time-related predictions or text, we use RNNs or Transformers; if we have a dynamic environment (like driving a car), we use reinforcement learning. Additionally, learning involves tackling different challenges:
-
Ensuring the model learns a general function and not just fitting the training data; this is handled through regularization;
-
Selecting the loss function based on the problem at hand; loosely speaking, the loss function is the error function between what we want (true value) and what we currently have (current prediction);
-
Gradient descent is the algorithm used to converge to the optimal function; deciding the learning rate becomes challenging because we want to move faster towards the optimal when we are far away, and slower when we are close to ensure convergence to the optimal and global minimum;
-
A large number of hidden layers need to deal with the vanishing gradient problem; architectural changes like skip connections and appropriate nonlinear activation functions help address this issue.
Computational Challenges
Now that we know deep learning is just learning complex functions, it brings other computational challenges:
-
To learn a complex function, we need a large amount of data;
-
To handle big data, we need fast computing environments;
-
We need infrastructure that supports such environments.
Using CPUs for parallel processing is insufficient to compute millions or billions of weights (also known as parameters in DL). Neural networks need to learn weights that require vector (or tensor) multiplication. This is where GPUs come into play, as they can perform parallel vector multiplication very quickly. Depending on the deep learning architecture, data size, and task at hand, we sometimes need 1 GPU, and sometimes data scientists need to make decisions based on known literature or by measuring the performance of 1 GPU.
By using the appropriate neural network architecture (number of layers, number of neurons, nonlinear functions, etc.) and a sufficiently large dataset, deep learning networks can learn any mapping from one vector space to another. This is what makes deep learning a powerful tool for any machine learning task.
Reference Content: https://venturebeat.com/2022/03/27/this-is-what-makes-deep-learning-so-powerful/