Tao Zhexuan Highly Recommends Copilot for Research

Kleisi from Aofeisi Quantum Bit | WeChat Official Account QbitAI

After endorsing GPT-4, Copilot has also been highly recommended by Tao Zhexuan.

He stated that while programming, Copilot can directly predict what he is going to do next.

With Copilot, research has become more convenient, and Tao Zhexuan used it to assist himself in completing his latest research results.

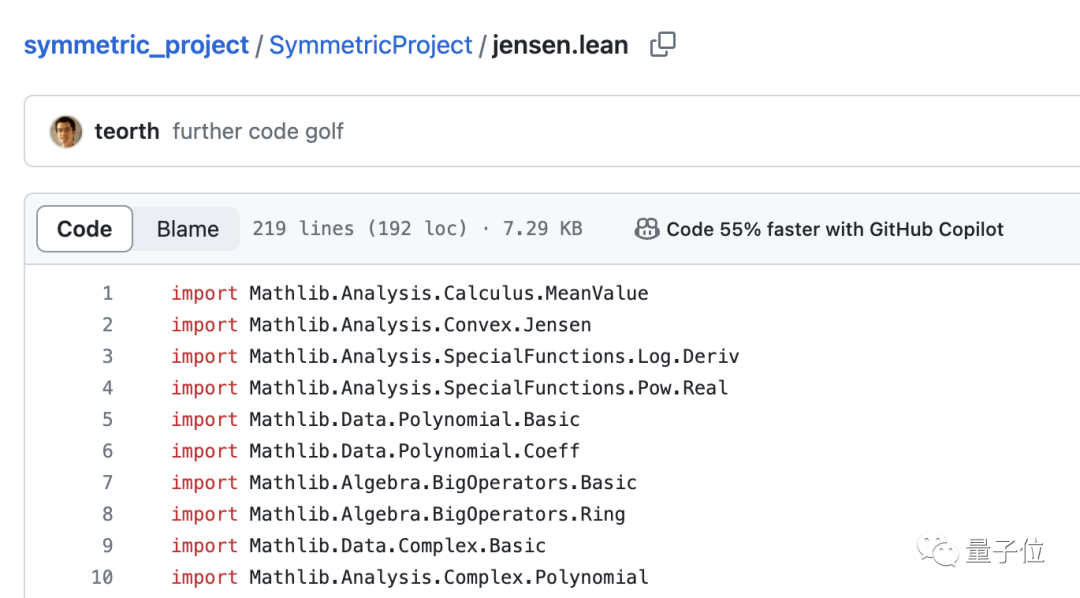
Tao Zhexuan said that in this paper, the relevant content actually only covers one page.

However, to complete the proof on this single page, he wrote over 200 lines of code, using the newly learned programming language Lean4.

According to Tao Zhexuan’s public GitHub page, Copilot has increased the speed of writing code by more than half.

Tao Zhexuan explained that he chose Lean4 because of its “rewrite strategy,” which allows for targeted local replacements of a long expression.

For example, if a complex function f(x) is defined, when we want to input the expression f(114514), we can directly use code to “rewrite” x as 114514.

Tao Zhexuan said that this feature is incredibly convenient compared to repeatedly inputting formulas in LaTeX.

So what new results does Tao Zhexuan’s “one-page proof” bring us?

New Inequality from One-Page Proof

This paper discusses the problem of the Maclaurin inequality.

The Maclaurin inequality is a classic inequality in mathematics, derived from the law that the arithmetic mean of non-negative real numbers is greater than or equal to the geometric mean, which can be expressed as:

Let y₁…y_n be non-negative real numbers. For k=1…n, define the mean S_k as (the number of terms in the denominator):

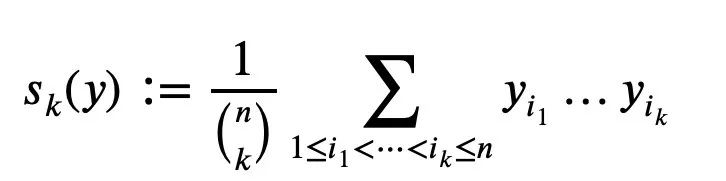
It appears as the normalization coefficient of an n-th degree polynomial with roots.

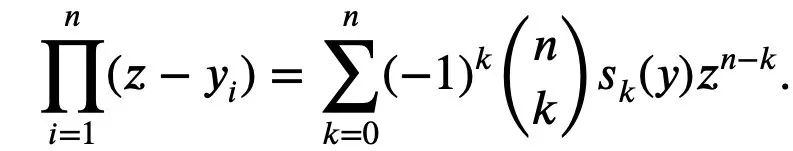
(Remember this formula; we will call it Formula 1)

Then the Maclaurin inequality can be expressed as:

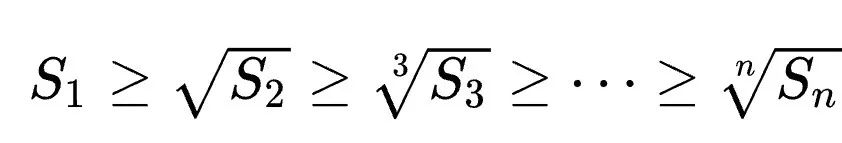
Where the equality holds if and only if all y_i are equal.

In calculus, there is also a classic Newton’s inequality:

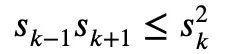
For any 1≤k<n, if the real variables y_1n are all non-negative, Newton’s inequality can simply describe the Maclaurin inequality:

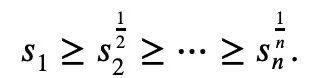
However, if this restriction is not added, allowing negative terms to exist, Newton’s inequality cannot represent the Maclaurin inequality.

Thus, regarding the potential existence of negative terms in Newton’s inequality, Tao Zhexuan proposed a new set of inequality variants:

For any r>0 and 1≤ℓ≤n, either Formula 2 or Formula 3 must hold.

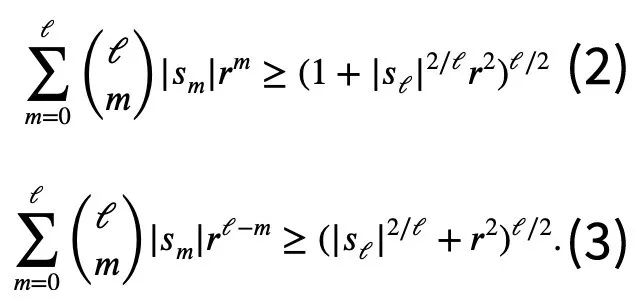
This is the content that Tao Zhexuan aims to prove on this one page, and the specific proof process is as follows:

Let’s construct a polynomial P(z) about the complex variable z:

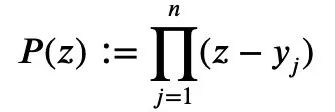
From the previous Formula 1 and the triangle inequality, we can obtain:

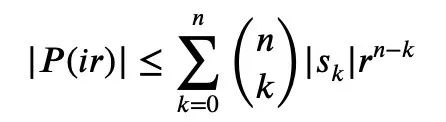
So we only need to establish a lower bound:

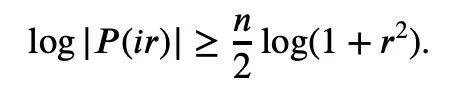
Taking the absolute value of P(z) and then taking the logarithm gives:

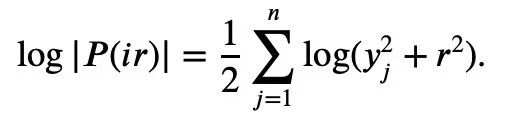
Since for any real number t, t ↦ log(e^t+a) is convex and a>0, we can obtain the inequality:

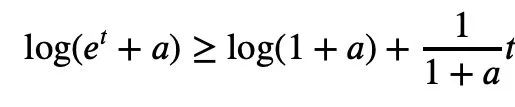
When a=r², t=2log y_j, we can derive:

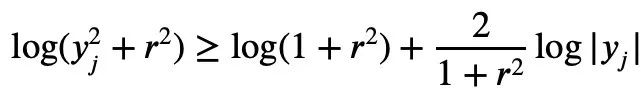
The above is the proof process provided by Tao Zhexuan; however, when the normalized |S_n|=1, the following holds:

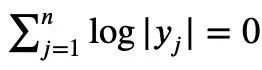
Next Step: Establishing a Refined Version

In addition to the “one-page proof” mentioned this time, Tao Zhexuan’s paper also proposed another new theorem, that for any 1 ≤ k ≤ ℓ ≤ n:

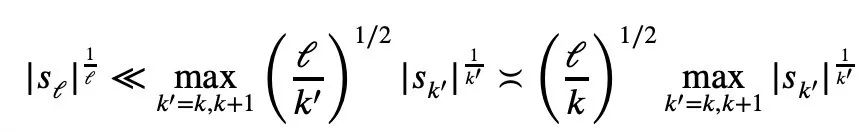
In the blog post, Tao Zhexuan revealed that his next plan is to propose a refined version of this inequality.

Tao Zhexuan said that the proof process would be “as simple as practice” and can be handled with calculus.

However, he also mentioned that there would be a small difficulty because this part of the proof process uses asymptotic notation.

What the new conclusion will be like, let us wait and see.

One More Thing

Tao Zhexuan is undoubtedly a loyal fan of AI tools, having recommended Copilot, GPT-4, and several other auxiliary tools.

This time, he also expressed new expectations for the development of large models, hoping that one day models can directly generate inequality variants.

Paper link: https://arxiv.org/abs/2310.05328

Reference link: https://mathstodon.xyz/@tao/111271244206606941

— End —

「Quantum Bit 2023 AI Annual Selection」 is starting!

This year, the Quantum Bit 2023 AI Annual Selection has established 5 award categories from three dimensions: enterprises, individuals, and products/solutions! Welcome to scan the QR code to sign up.

MEET 2024 conference has been launched! Click here for details.

Click here👇 to follow me, remember to star it~

One-click triple connection to “share”, “like” and “view”

Cutting-edge technological advancements every day ~