Click above to subscribe to “China Computer Federation” easily!
Source: “China Computer Federation Communication”, 2017, Issue 11, “Column”
GAN: Generative Adversarial Networks
Generative Adversarial Networks (GANs) are a concept proposed by Ian Goodfellow in 2014 that uses adversarial methods to generate data. Imagine we have two images, one real and one fake. How can humans determine whether this painting is forged or real? For example, in Figure 1, the issue with the forgery is that the “person in the painting” is not depicted correctly; it is not a person but a rabbit, so it can be considered fake. The forger thinks: this is where the person should be painted, if I improve this area, I can create a more realistic painting next time. After he finishes the painting, people may find another issue again. This iterative process of continuous improvement can enhance the capabilities of the generator (the forger), while the detective’s skills also improve.
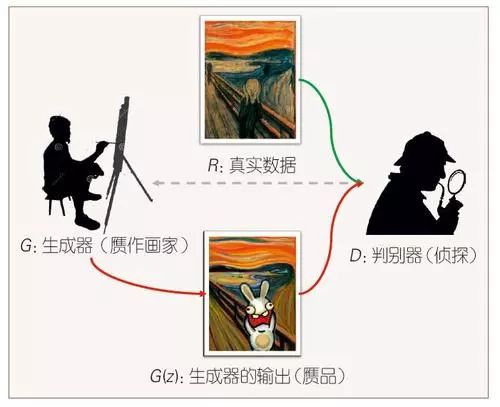
Figure 1 Schematic of Generative Adversarial Networks
GANs have achieved great success in tasks such as computer image generation. In addition, GANs also involve many other topics, such as encryption and security, robotics, and even astrophysics. The development direction of GANs is constantly deepening and expanding, moving from traditional computer vision into other fields. Yann LeCun mentioned in an interview that one of the most noteworthy ideas in deep learning over the next decade is GANs, as this method has made many previously impossible tasks possible.
Background of GAN Proposal
Research on Intelligence
In the more than sixty years of development of artificial intelligence, researchers can generally be divided into two schools: the so-called “Neats” and “Scruffies.” The “Neats” believe that to establish an artificial intelligence system, one must first thoroughly understand its formal characteristics, leaning towards using mathematics, especially mathematical logic, as analytical tools to study artificial intelligence, pursuing transparency and methods that can prove causal relationships in constructing intelligent systems. In contrast, the “Scruffies” focus on functionality and efficiency, adopting a more “evolutionary” view, paying less attention to “proof” or “explanation,” and believing that it is most important to get started, to first establish such “intelligent” entities, from the initial computational neural methods, heuristic intelligent program design, multi-agent systems, to today’s hot deep learning and various computational intelligence methods. One of the focal points of the debate between the two schools is whether simple program design can serve as a theoretical foundation for artificial intelligence1. Naturally, revealing the essence of intelligence theoretically and building intelligent machines engineering-wise has been a common goal for all artificial intelligence researchers over the long term.
In recent years, “Scruffies” methods represented by deep learning have achieved breakthroughs in speech analysis, image recognition, and natural language processing that “Neats” methods have long failed to realize. Coupled with the big data boom, this has sparked great interest in data-driven artificial intelligence methods. The question is, where does big data come from? What are the costs? And how do we transition from data to intelligence?
Generally speaking, the starting points for researching artificial intelligence can be divided into two categories. One approach studies the generated things from the perspective of human understanding of data. Since human experience is very limited, we must learn from some mathematical or intuitively perceptible examples from reality. When creating generative models, we predefine a distribution (such as a Gaussian distribution), assuming that images conform to this distribution, with only the parameters’ distribution being unknown; we can fit this distribution through data. The other approach allows machines or models to directly understand this data, without making assumptions about the data, but instead letting a model generate data and then judging whether this data is correct or not, whether it resembles real data or differs too much from real data, and based on this judgment, we repeatedly correct the model. Previous research on generative models mainly started from the perspective of human understanding of data, hoping to design models using explicit distribution assumptions. GANs can be said to be the first widely known model that fits data from the perspective of machines or data: we no longer provide it with any data model distribution, but learn directly.
GAN Theory and Implementation
Based on the above technology, Goodfellow proposed the idea of GAN. Specifically, design a game involving two players, one being the generator (G), which generates images that appear to come from the training samples, and the other player is the discriminator (D), which determines whether the input images are indeed from the training samples or generated. The overall framework of GAN is shown in Figure 2. This framework includes a random variable in a latent spacez—it may be sampled from a Gaussian distribution or may be a latent variable with some informational significance, with a dimension potentially smaller than that of real samples or the real space. The latent variable is input into the generator, which is a differentiable functionG(z). G(z) and the real samplesx are both fed into the discriminator, which tries to judge whether the generated image is a fake image. Meanwhile, G will try to trick the discriminator into thinking that this image comes from real images. The discriminator will backpropagate its gradients to G and D, which is why it is emphasized that both G and D are differentiable functions; otherwise, the error cannot be backpropagated. This is the original structure of GAN.
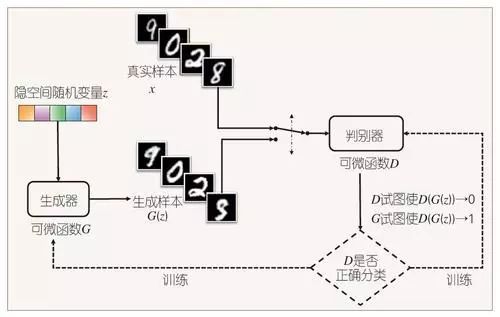 Figure 2 The Overall Framework of GAN
Figure 2 The Overall Framework of GAN
In the original GAN, both the discriminator and generator are fully connected networks used for generating images. Currently, various applications mainly use convolutional neural networks (CNNs) to design input-output images.
Compared with traditional models, GAN has the following advantages. First, the complexity and dimensionality of the generated data are linearly related. If we want to generate a larger image, we do not face an exponentially increasing computational load as in traditional models; it is merely a linear increase in the neural network process. Second, there are very few prior assumptions, which is the biggest advantage compared to traditional models. The most prominent difference from previous models is that GAN does not make any explicit parameter distribution assumptions about the data. Third, it can generate higher quality samples. However, GAN also has disadvantages compared to traditional models. Generally speaking, traditional discriminative models are also optimization functions, and for convex optimization, there is certainly an optimal solution. However, GAN seeks a Nash equilibrium point in a two-player game2. For a given strategy, such as a neural network, inputting a value will certainly yield a determined output, but it may not be possible to find a Nash equilibrium point. Finding and optimizing the Nash equilibrium point in GAN is a very challenging task, and there is currently a lack of research in this area.
Development and Application of GAN
The Convergence Problem of GAN
Currently, the non-convergence issue is the main problem with GANs. In practical training, it often requires setting many parameters to balance the capabilities of G and D to achieve convergence. The non-convergence problem mainly manifests in two ways. First, the gradient vanishing problem: the original GAN uses classification error as a measure of the closeness between the real distribution and the generated distribution. Under the condition of an optimal discriminator, the generator’s loss function is equivalent to minimizing the JS divergence between the real and generated distributions. However, it has been proven that when the overlapping area between the real distribution and the generated distribution is negligible, the JS divergence becomes a constant, and the gradient obtained by the generator is 0. Second, the mode collapse problem, meaning the generator may produce the same data instead of diverse data. This issue primarily arises because the gradient descent method used in optimization does not differentiate between min-max and max-min, leading the generator to prefer generating some repeated but safe samples. However, we hope the generated samples are as diverse as the real samples. These problems can be addressed by designing better network structures, different metrics, or some training tricks, which are generally used in combination. For example, WGAN achieves good results by using Wasserstein distance instead of JS divergence while employing weight clipping tricks. How to systematize, formalize, and toolize many tricks is a key step in determining whether GAN can be further popularized.
Reinforcement Learning and Imitation Learning
First, let’s talk about reinforcement learning. A 2016 paper discusses the similarities between GAN and Actor-Critic3. The network structure of GAN is similar to Figure 3(a), while Actor-Critic, as a method of reinforcement learning, has a structure as shown in Figure 3(b).
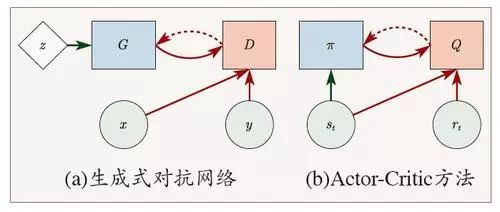 Figure 3 Comparison of GAN and Actor-Critic
Figure 3 Comparison of GAN and Actor-Critic
For GAN, z is input to G, and then D judges whether the output of G is correct. For Actor-Critic, the state from the environment is input to π, which then outputs to Q, where the critic evaluates the policy. The difference between reinforcement learning and GAN lies in z and st, since the state of the environment has a certain randomness; only one state input is sufficient, while in GAN, the state and the random signal are separated. We see that these two methods have structural consistency, but do they also have training method consistency? From practical situations, they indeed do; many techniques used in Actor-Critic training can be transplanted to GAN training, and they are generally effective.
On the other hand, GAN can provide some data for reinforcement learning. In reinforcement learning, data is scarce, and it may take a long time to obtain such data, or it may require a high cost to collect data, so we can use the data generated by GAN for reinforcement learning.
 Figure 4 Generative Adversarial Imitation Learning
Figure 4 Generative Adversarial Imitation Learning
Generative Adversarial Imitation Learning (GAIL) is another interesting application of GAN, with its structure illustrated in Figure 4. In previous imitation learning, it was necessary to learn a reward function from expert samples and then use this reward function to train a reinforcement learning agent. Generative Adversarial Imitation Learning borrows from the idea of GAN, not directly learning the reward function, but rather learning the mapping from state to action (st, at). In GAIL, the policy network is analogous to G in GAN, and at corresponds to G(z), allowing for direct imitation of expert behavior without the need for intermediary steps.
GAN and Parallel Intelligence
New IT and the Third Axial Age
The reason I am interested in GAN and want to work on it myself is that GAN effectively serves as a means to produce data by paralleling truth and falsehood, unifying this contradiction. This aligns with my advocacy for a parallel approach to intelligence and learning: GAN provides a concrete and detailed pathway for parallel intelligence4 and parallel learning5, while parallel intelligence and parallel learning propose directions for the further development of GAN. In traditional thinking, models are analytical tools, and modeling is for analysis; however, GAN and the parallel breakthroughs based on ACP6 break this understanding, turning models into “factories” for producing data, transitioning from the Newtonian path of “big laws, small data” to the Mertonian path of “big data, small laws”7.
 Figure 5 Three ITs and Three Worlds: Parallel Technology and Parallel Era
Figure 5 Three ITs and Three Worlds: Parallel Technology and Parallel Era
In fact, AlphaGo has also pointed the way for us from the Newtonian to the Mertonian path. Following this path leads us to the future of the intelligent industry. After AlphaGo, IT is no longer just information technology; that is old IT; it is now intelligent technology (Intelligent Technology), which is the new IT. Let’s not forget that 200 years ago, IT meant industrial technology, and today it can be referred to as old IT. The future is a parallel coexistence of the three ITs, closely related to Popper’s theory of three worlds. We only know the physical world and the psychological world, but Popper tells us there is a third world— the artificial world, in which industrial, informational, and intelligent “old, obsolete, and new” IT technologies are the main technologies for developing these three worlds, which is why today is the era of artificial intelligence, and data has become the “oil reserve” (see Figure 5).
I call this belief the “AlphaGo Thesis.” Because 80 years ago, there was a “Church-Turing Thesis”8, commemorating the Lambda calculus and finite state machines (Turing machines) of Church and Turing, which are mathematically equivalent despite differing in complexity. This led von Neumann to propose the “von Neumann architecture,” the structure of the first digital computer in the world, which we still draw on today, enabling the development of the computer and information industry to its current state. I believe the effect of the AlphaGo thesis on the intelligent industry is equivalent to that of the Church-Turing thesis on the information industry.
Looking back at human history, we have developed from agricultural technology around the physical world to industrial technology, and around the psychological world, we have developed information technology. Today, we are at the threshold of developing the third world, the artificial world, where big data, population, and intelligence become resources, leading intelligent technology to become the new IT. From the industrial age to the information age and now to the intelligent age, we are entering a parallel world.
This is a brand new era, which I call the third axial age. The axial age is a concept proposed by Karl Jaspers 70 years ago in his book “The Origin and Goal of History,” which had a tremendous impact on human thought. However, I believe his axial age only represents the first axial age of the physical world; each of the three worlds should have its own axial age. The second axial age of the psychological world spans over 500 years from the Renaissance to the establishment of the modern scientific system, while the third axial age of the artificial world actually began with the discovery of Gödel’s incompleteness theorem, followed by the initiation of artificial intelligence research. The three axial ages represent humanity’s great awakening in humanity, rationality, and intelligence, along with the subsequent breakthroughs in philosophy, science, and technology. The paradigms of human thought and recognition have shifted from eternal divine recognition to scientific recognition of causal laws, and now to data recognition of associative relationships. We need data; we must generate data; we must be able to extract knowledge and intelligence from data.
Therefore, I believe that algorithms like GAN are just the beginning. I hope everyone can master such methods well and also create their own methods. Transforming small data into big data, and big data into small knowledge. Achieving the leap from the Newtonian system to the Mertonian system, from the parallel of truth and falsehood to the parallel of reality and illusion, moving towards parallel learning and parallel intelligence.
Parallel Intelligence and Parallel Learning
What we are doing here is artificial organization, encompassing generalized models and software-defined models. There are not only physical models but also behavioral models. How do we transform into big data? It relies on computational experiments. Many experiments cannot be conducted physically due to cost, legal, ethical, and scientific constraints. By providing extensive feedback on the behavior of models and actual behaviors in the Social Physical Information Space (CPSS), we can achieve parallel learning and realize parallel intelligence, which is based on the ACP parallel philosophy.
 Figure 6 Parallel vs. Parallel: From GAN to Parallel Intelligence
Figure 6 Parallel vs. Parallel: From GAN to Parallel Intelligence
Therefore, all future systems should be actual plus artificial. The relationship between reality and illusion can be one-to-one, many-to-one, one-to-many, or many-to-many. This differs from traditional parallelism, which is about dividing and conquering, while parallelism is about expanding and governing.
In fact, GAN is the simplest parallel system, but it is not complete on both ends. It uses a discriminator to achieve the physical system and a generator to create an artificial system, realizing the parallel of truth and falsehood. For me, this is a simple prototype of future parallel machines. Its further development could bridge the three worlds: the physical world, the psychological world, and the artificial world, achieving the leap from Newton to Merton, leading humanity into the intelligent industry and the wise society.
(This article was organized by Bai Tianxiang and Lin Yilun, doctoral students at the State Key Laboratory of Management and Control for Complex Systems, Institute of Automation, Chinese Academy of Sciences. It is based on the author’s recording at the Frontiers Workshop on Intelligent Automation of the Chinese Automation Society, with some edits.)
Footnotes:
1 D. Partridge, “Workshop on the foundations of AI: Final report,” AI. Magazine., vol. 8, no. I, pp. 55-59, Spring 1987.
2 Nash equilibrium is a strategy combination such that each participant’s strategy is the optimal response to the strategies of others at the same time.
3 D. Pfau and O. Vinyals, “Connecting Generative Adversarial Networks and Actor-Critic Methods,” arXiv:1610.01945 [cs, stat], Oct. 2016.
4 Wang F Y, Wang X, Li L X, Li L. Steps toward Parallel Intelligence. IEEE/CAA Journal of Automatica Sinica, 2016, 3(4): 345-348.
5 Li L, Lin Y, Zheng N, Wang F Y. Parallel Learning: a Perspective and a Framework. IEEE/CAA Journal of Automatica Sinica, 2017, 4(3): 389-395.
6 Artificial system, Computational experiments, Parallel execution
7 Famous American sociologist who proposed Merton’s Law: due to feedback between beliefs and behaviors, predictions directly or indirectly contribute to their own realization.
8 The Church-Turing Thesis is a thesis in computer science named after mathematicians Alonzo Church and Alan Turing. The fundamental point of this thesis is that all computations or algorithms can be executed by a Turing machine. This thesis is generally assumed to be true and is also known as the Church thesis or Church conjecture and Turing thesis.
Author:

Wang Feiyue
Distinguished Member of CCF. Vice President and Secretary-General of the Chinese Association of Automation, Researcher at the Institute of Automation, Chinese Academy of Sciences. Research areas: intelligent control, social computing, parallel systems, knowledge automation, etc.
