Mathematical Derivation of GAN
Author: Sherlock
Source: Machine Learning Algorithms and Natural Language Processing
Previously, we discussed the basic idea of GAN. Recently, I reviewed some GAN papers and happened to watch a course by Professor Li Hongyi, finding the mathematical derivation quite interesting, so I decided to write it down for future reference.
First, we need some preliminary knowledge: KL divergence, which is a concept in statistics that measures the similarity between two probability distributions. The smaller it is, the closer the two distributions are. For discrete probability distributions, it is defined as follows:
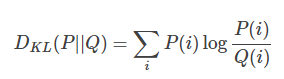
For continuous probability distributions, it is defined as follows:
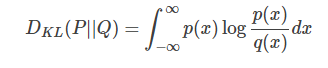
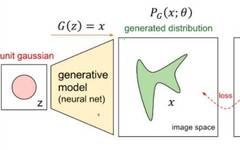
According to what we discussed earlier, what we need to do is as shown in the following figure:
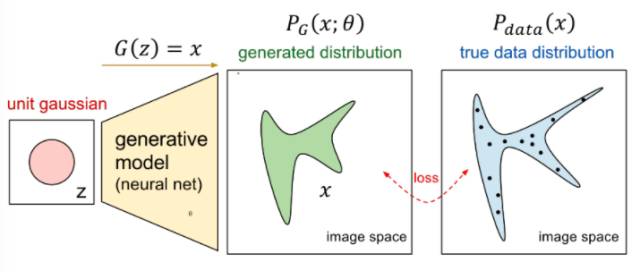
We want to transform a random Gaussian noise z through a generator network G to obtain a generated distribution that is similar to the real data distribution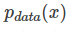 
.
The parameters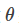 
are determined by the network parameters, and we hope to find θ∗ such that 
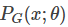is as close as possible.
We sample m points from the real data distribution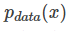 
and, based on the given parameters 
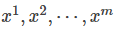, we can compute the following probability 
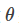. The likelihood of generating these m sample data is thus:
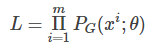
What we want to do is find θ∗ to maximize this likelihood estimate.
And how do we calculate PG(x;θ)?
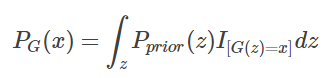
The I inside represents the indicator function, which is:
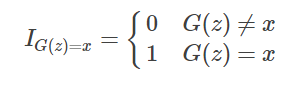
Thus, we actually cannot compute this PG(x), which is the fundamental idea of generative models.
-
Generator G
-
G is a generator, given a prior distribution Pprior(z), we hope to obtain the generated distribution PG(x). This is difficult to achieve through maximum likelihood estimation.
-
Discriminator D
-
D is a function that measures the difference between PG(x) and Pdata(x), which replaces maximum likelihood estimation.
First, we define the function V(G, D) as follows:
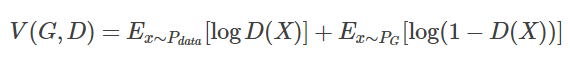
We can derive the optimal generative model using the following expression:
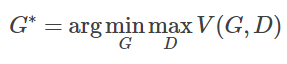
Doesn’t it feel confusing? Why does defining a V(G, D) and then taking max and min yield the optimal generative model?
First, we only consider maxDV(G,D) and see what it means.
Given G, we need to choose a suitable D such that V(G, D) can achieve its maximum value; this is simple calculus.
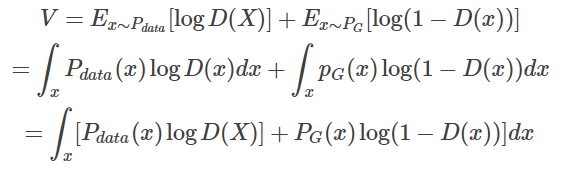
For this integral, to maximize it, we want the term inside the integral to be maximized for given x, meaning we want to obtain an optimal D∗ that maximizes the following expression:
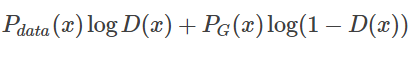
Given the data and G, Pdata(x) and PG(x) can be seen as constants, which we can denote as a and b. Thus, we can derive the following expression:
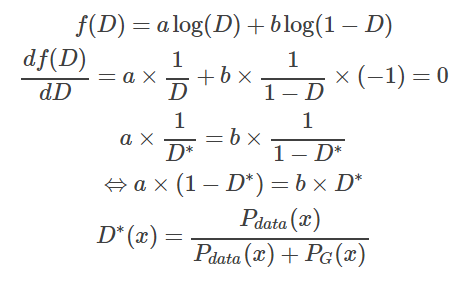
This allows us to determine D that maximizes V(D) given G, and substituting D back into the original V(G, D) yields the following result:
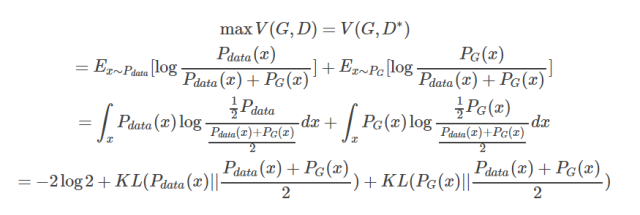
At this point, we have already derived why this measurement is meaningful, as we take D to maximize V(G,D).
The maximum value is composed of two KL divergences, meaning this maximum value measures the degree of difference between PG(x) and Pdata(x). Therefore, we take:
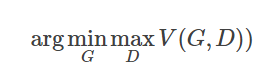
This allows us to achieve G such that the difference between the two distributions is minimized, thus naturally generating a distribution that closely resembles the original distribution.
At the same time, this also avoids the computation of maximum likelihood estimation, so GAN fundamentally changes the training process.
Blog address: https://sherlockliao.github.io/2017/06/20/gan_math/
☞ Halmus: How to Conduct Mathematical Research
☞ Mark Zuckerberg’s 2017 Harvard Commencement Speech
☞ Applications of Linear Algebra in Combinatorial Mathematics
☞ Have You Seen the Real Phillips Curve?
☞ The Story of Support Vector Machines (SVM)
☞ Is the Mathematics in Deep Neural Networks Too Difficult for You?
☞ How Much Mathematics Do You Need to Know for Programming?
☞ Chen Shengshen – What is Geometry?
☞ A Review and Outlook on Pattern Recognition Research
☞ The Theory of Surfaces
☞ What is the Significance of the Natural Base e?
☞ How to Explain Support Vector Machines (SVM) to a 5-Year-Old?
☞ Chinese-American Genius Mathematician Terence Tao’s Autobiography
☞ Algebra, Analysis, Geometry, and Topology: The Three Major Methodologies of Modern Mathematics
We welcome submissions to the WeChat public account: The Beauty of Mathematical Algorithms
Submissions should involve mathematics, physics, algorithms, computer science, programming, and related fields.
Upon acceptance, we will offer remuneration.
Submission email: [email protected]