Mastering Stratego Through Model-Free Multiagent Reinforcement Learning

“DeepNash is an autonomous agent capable of learning Stratego from scratch to reach human expert level. Stratego is one of the few iconic board games that artificial intelligence (AI) has yet to master. This game not only has a vast game tree, but DeepNash also needs to make decisions under conditions of incomplete information. Decisions in Stratego are made based on a large number of discrete actions, and typically require hundreds of decisions before a player wins, with no clear connection between actions and outcomes. The situations in Stratego cannot be easily decomposed into manageable subproblems like in poker. For decades, Stratego has posed a significant challenge in the field of AI, with existing AI methods barely reaching amateur levels in the game. DeepNash uses a model-free, game theory-based deep reinforcement learning approach to learn the game through self-play. Among these, the regularized Nash dynamics (R-NaD) algorithm is a key component of DeepNash, which converges to an approximate Nash equilibrium state by directly modifying the underlying multi-agent learning dynamics rather than ‘oscillating’ around it. DeepNash has defeated existing state-of-the-art AI methods in Stratego and achieved human expert level.”

Paper Title:Mastering the Game of Stratego with Model-Free Multiagent Reinforcement LearningPaper Link:https://arxiv.org/abs/2206.15378Authors:Julien Perolat, Bart de Vylder, et al.

Table of Contents1. Introduction2. Method 2.1 Learning Method 2.2 R-NaD Algorithm 2.3 DeepNash: Scalable R-NaD 2.3.1 Incomplete Information Games 2.3.2 Model-Free Reinforcement Learning and Regularized R-NaD3. Conclusion 3.1 Evaluation on Gravon Platform 3.2 Evaluation Against State-of-the-Art Stratego Robots 3.3 Demonstration of DeepNash’s Capabilities 3.3.1 Deploying Pieces 3.3.2 Trade-offs Between Information and Material 3.3.3 Deceptive Behaviors and Bluffing4. Summary

1

Introduction

Since the birth of artificial intelligence (AI), the level of mastery over board games has always been an important metric. Board games can measure how humans and machines devise and execute strategies in controlled environments. For decades, as one of the cores of AI, long-term planning capabilities have achieved significant success in complete information games such as chess, checkers, xiangqi, and go, as well as in incomplete information games like poker and Scottish games. Figure 1a visually represents the phases and mechanics of the game. This game faces two key challenges. First, the game tree of Stratego has 10⁵³⁵ possible states, more than the 10¹⁶⁴ possible states of no-limit Texas Hold’em (a well-studied incomplete information game) and the 10³⁶⁰ possible states of go. Second, at the start of the game, each player has 10⁶⁶ possible deployments to reason about, while poker only has 10³ possible pairs of cards. Unlike complete information games like go and chess, which do not have a private deployment phase, Stratego is much more complex. Therefore, it is impossible to apply the current best model-based complete information planning techniques, nor can the game be decomposed into independent incomplete information search states.Due to these reasons, Stratego presents unprecedented difficulty in studying strategic interactions. Like most board games, Stratego tests our ability to make relatively slow, careful, and logical decisions consistently. Due to the complexity of the game’s structure, there has been virtually no progress in AI research on Stratego. Agents can only reach levels comparable to amateurs. One of the significant challenges in AI research has been how to learn end-to-end and make optimal decisions in Stratego without human demonstration data.In this paper, we will introduce DeepNash, an agent capable of learning Stratego in a model-free manner through self-play without human demonstrations. DeepNash has defeated the current state-of-the-art AI agents and achieved human expert-level performance in the game’s most complex variant—Stratego Classic. The core of DeepNash is the regularized Nash dynamics method, a systematic, model-free reinforcement learning algorithm. DeepNash combines R-NaD with deep neural network architectures and converges to a 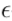-Nash equilibrium, meaning it learns to play at a high competitive level and is not easily exploited by other players. All incomplete information games have a mixed strategy Nash equilibrium that assigns a mixed (or random) strategy to all players, such that as long as other players do not deviate from their strategies, no player will benefit from it. While it is sufficient to take deterministic decisions to maximize the value of the equilibrium strategy in complete information two-player zero-sum games, this approach is theoretically unreasonable when dealing with incomplete information games. In such games, other strategies need to be deployed to better reflect decision processes in the real world. As von Neumann described, “real life contains bluffs and little strategies, ask yourself what others think I will do.” Figure 1b provides an overview of DeepNash.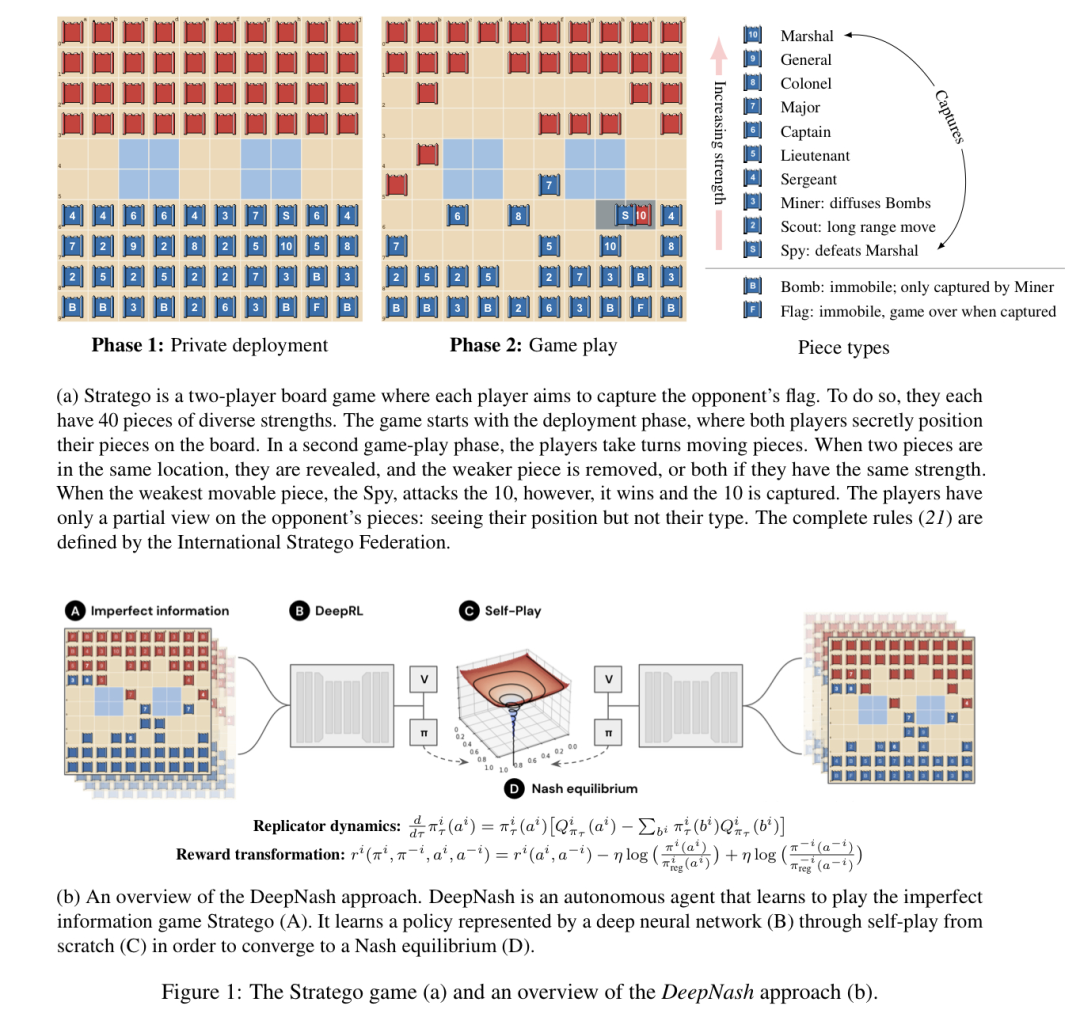(a) Stratego is a two-player board game where the objective is to capture the opponent’s flag. Each player has 40 pieces of varying strengths. The game starts with a deployment phase, where both players secretly place their pieces on the board. In the second phase of the game, players take turns moving their pieces. When two pieces are in the same position, they are revealed, and the weaker piece is removed; if they are of equal strength, both are removed. However, when the weakest piece attacks the number 10, the spy wins and the 10 is captured. Players do not fully understand the opponent’s pieces: they can see the positions of the pieces but not their types. The complete rules are customized by the International Stratego Federation.We have deployed the model-free reinforcement learning method DeepNash on the Gravon game platform to compete against various top Stratego robots and human expert players, systematically evaluating its performance. DeepNash has defeated all currently developed state-of-the-art robots for Stratego with a winning rate of over 97%, and achieved a winning rate of 84% on the Gravon platform, ranking in the top three for the year (2022) and historically. This is the first time an AI algorithm has reached human expert level in such a complex board game without deploying any search methods in the learning algorithm.

2

Method

DeepNash adopts an end-to-end learning approach to tackle the problem of Stratego. It employs an integrated deep reinforcement learning and game theory approach, incorporating the deployment phase (i.e., tactically placing pieces on the board at the start of the game, see Figure 1a) into the learning during the game phase. The goal of the agent is to learn an approximate Nash equilibrium through self-play. Designing a strategy that is robust in the worst-case scenario is often a good choice, and Nash equilibrium guarantees that the agent performs well even in the worst-case scenarios, effectively competing against humans in two-player zero-sum games. In complete information games, search techniques aided by reinforcement learning, i.e., model-based learning techniques, have demonstrated superior capabilities in go and chess. However, finding Nash equilibrium in incomplete information games requires estimating the private information of opponents from public states, and the computational power of existing search techniques cannot meet the demands of Stratego. Therefore, we propose a new method that combines model-free reinforcement learning in self-play with game-theoretic algorithmic ideas into regularized Nash dynamics (R-NaD). The model-free part means we do not need to explicitly construct a model of the opponent, tracking belief states (calculating the likelihood of the opponent’s states), while the game-theoretic part supports the reinforcement learning method by modifying the dynamics system to guide the agent’s learning behavior towards Nash equilibrium. The main advantage of this combined approach is that it does not require explicitly constructing a model of private states from public states. However, combining this model-free reinforcement learning method with R-NaD is still quite complex and challenging. Figure 1b illustrates this combined approach in DeepNash. In the following subsections, we will use fundamental concepts from game theory to provide more details for readers who are unfamiliar.

2.1 Learning Method

We learn Nash equilibrium in Stratego through self-play and model-free reinforcement learning. The idea of combining model-free reinforcement learning with self-play has been attempted before, but stabilizing such learning algorithms when scaling to more complex games (e.g., capture the flag, Dota, and StarCraft) is challenging. Training on past versions of the agent or incorporating reward shaping or expert data into the training algorithm can stabilize learning algorithms, but these methods lack theoretical foundations, are difficult to tune, and are not easily generalizable to new games.Moreover, in games like Stratego, defining a loss that can converge to Nash equilibrium without introducing large-scale computational issues is difficult. For instance, minimizing availability (a measure of distance to Nash equilibrium) requires estimating the agent’s best response during training, which is hard to compute in Stratego. However, it is possible to define a learning rule with a dynamical system that has a Lyapunov function. This function is proven to gradually decrease during the learning process, ensuring convergence to a fixed point. Using deep neural networks to extend this method is the core idea behind the R-NaD algorithm and the key to DeepNash’s success.

2.2 R-NaD Algorithm

The R-NaD learning algorithm used in DeepNash is based on the regularization idea for convergence purposes. R-NaD relies on three key steps (see Figure 2b):First, based on the regularized strategy π_reg , we perform reward transformation to obtain a modified game with rewards: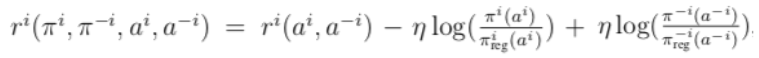 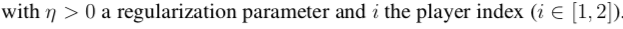Note that this transformed reward depends on the strategy itself.Second, in the dynamics step, we allow the system to evolve according to replicator dynamics on this modified game. Replicator dynamics is a descriptive learning process in evolutionary game theory, analogous to RL algorithms, also known as Follow the Regularized Leader, defined as follows: 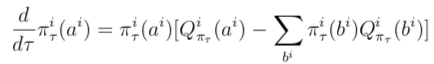for the quality or fitness of actions.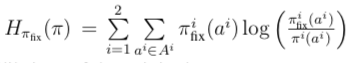These dynamics increase the likelihood of taking high-fitness actions (relative to other actions). Due to the reward transformation, this system has a unique fixed point π_fix and guarantees convergence to it. This can be proven using a Lyapunov function.However, this fixed point is still not the Nash equilibrium of the original game.In the final update step, the obtained fixed point is used as the regularized strategy for the next iteration. Repeating these three steps generates a sequence of fixed points, which can be proven to converge to the Nash equilibrium of the original game. Figure 2c illustrates the R-NaD algorithm in the two-player penny game (see the return rate table in Figure 2a).The first iteration starts from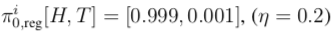, and the replicator dynamics converge to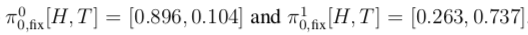. Figure 2c shows the evolution of the logarithm of the Lyapunov function, illustrating its decrease during the learning process.The following figure illustrates the three iterations of R-NaD.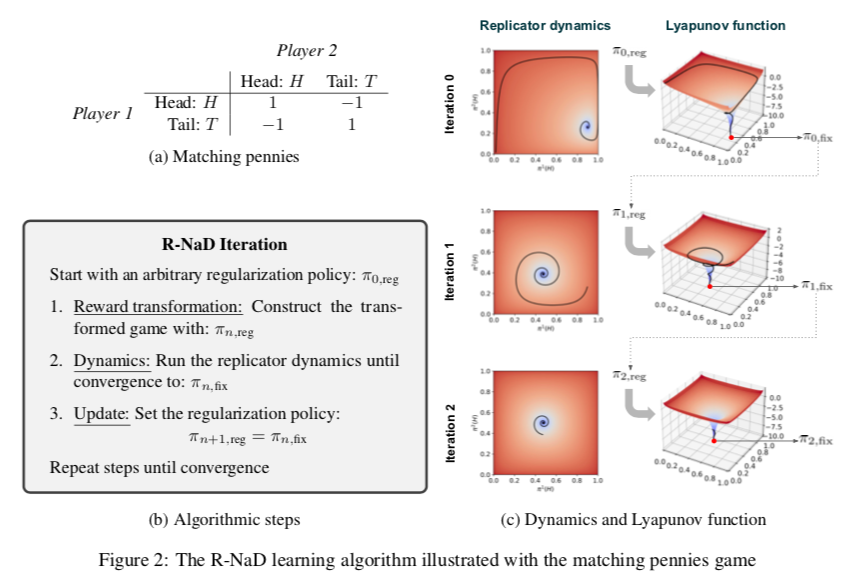Figure 2: Illustrating the R-NaD learning algorithm with the penny game

2.3 DeepNash: Scalable R-NaD

DeepNash consists of three parts:(1) A model-free RL algorithm implemented with deep convolutional networks and the core training component R-NaD;(2) Fine-tuning the learned strategies to reduce the probability residual of taking extremely unlikely actions;(3) Post-processing during testing to filter out low-probability actions and correct errors.First, we briefly introduce some basic background information about incomplete information games to understand how R-NaD is scaled into a deep learning model. Then, we continue to interpret the three algorithmic steps of R-NaD and summarize how they are implemented in the neural architecture.2.3.1 Incomplete Information GamesIn a two-player zero-sum incomplete information game, two players (player i = 1 or i = 2) take turns acting. At round t, players receive a reward signal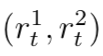, the current player i = ψt chooses an action a_t by observing the game state o_t and based on a parameterized policy function π（.|ot）.In model-free reinforcement learning, the trajectory 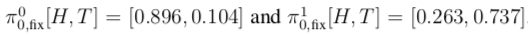is the only data allowed for the agent to learn parameterized policies.2.3.2 Model-Free Reinforcement Learning and Regularized R-NaDDeepNash uses deep learning architectures to extend the algorithm of R-NaD. It performs three algorithmic steps similar to previous NFGs:(1) Reward transformation step, modifying rewards;(2) Dynamics step, allowing convergence to a fixed point;(3) Update step, where the algorithm updates the strategy that defines the regularization function.Neural Structure and State Representation:DeepNash’s network consists of several parts: a U-Net backbone with residual blocks and skip connections, and four heads constructed from simplified structures of the backbone, with the last layer modified to generate outputs of appropriate shapes. The first DeepNash head outputs the value function as a scalar, while the other three heads encode the agent’s strategy by outputting their action probability distributions during deployment and gameplay.The observed state is encoded as a spatial tensor composed of the following parts: DeepNash’s own pieces, publicly available information about DeepNash and its opponent’s pieces, and the encoding of the last 40 actions. Given previous games, these public pieces of information still retain historical information of the game. The observed state includes a tensor containing 82 frames of information. The structure of the observation tensor is shown in Figure 3.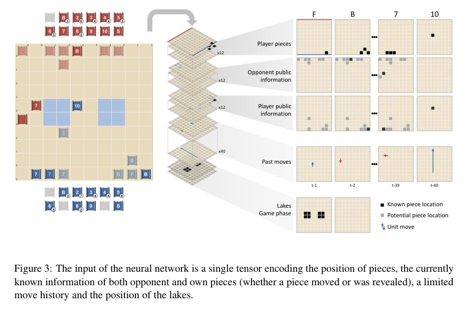Figure 3: The input to the neural network is a single tensor encoding the positions of pieces, information about currently known opponent and own pieces (whether pieces have moved or been revealed), limited move history, and the locations of lakes.R-NaD Cycle:Given the trajectory, starting from the initial strategy π_{m = 0, reg} at round t, rewards start to transform.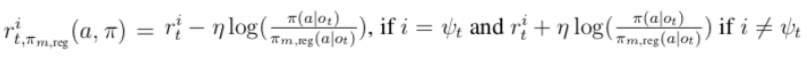The dynamics step of DeepNash consists of two parts. The first part estimates the value function by adjusting the v-trace estimator; the second part updates the strategy using Neural Replicator Dynamics (NeuRD) based on the estimated action value from the v-trace estimator.After a certain number of learning steps, an approximate fixed-point strategy π_{m, fix} is obtained, which is then used as the next regularized strategy π_{m+1, reg} = π_{m, fix} using a smooth transition from the reward transformation of step m to that of step m+1, repeating the above three steps.Fine-tuning:Direct learning using the above method will converge to a relatively satisfactory solution, but this solution can be slightly affected by low-probability errors. These errors occur because the softmax projection used to calculate the strategy from the logarithm assigns a non-zero probability to each action. To mitigate this issue, we fine-tune by thresholding and discretizing the action probabilities during training.

3

Conclusion

This section summarizes the evaluation results of DeepNash against human experts and current state-of-the-art Stratego robots.For the former, we used the Gravon online game server, which is very popular among Stratego players. For the latter, DeepNash was tested against eight Stratego AI robots. This paper also analyzes the capabilities of the agent in the game, including deployment, bluffing, and the exchange of material and information.

3.1 Evaluation on Gravon Platform

Gravon is an internet platform for human players and is the largest online platform for Stratego to date, where the strongest players compete. The Gravon platform uses the same rating system as the World Championship of the International Stratego Federation (i.e., Kleier rating). Gravon offers two rankings: one for historical classic Stratego and one for the 2022 Stratego challenge ranking. To enter the leaderboard, Gravon imposes some restrictions to ensure that players always face equally matched opponents.In early April 2022, over a two-week period, DeepNash competed against top human players, producing 50 ranked matches for evaluation. Of these matches, DeepNash won 42 (i.e., 84%). In the 2022 Stratego challenge ranking, it achieved a rating equivalent to 1799, earning a third-place position (the top two ratings were 1868 and 1831). In the historical classic Stratego ranking, DeepNash’s rating was 1778, placing it third among all ranked players in history (the top two ratings were 1876 and 1823). This leaderboard rating includes all ranked games since 2002.These results confirm that DeepNash has reached human expert level in Stratego, solely through self-play without guidance from existing human data.

3.2 Evaluation Against State-of-the-Art Stratego Robots

DeepNash was also evaluated against several existing Stratego computer programs. Probe is a three-time champion of the computer Stratego World Championship (2007, 2008, 2010); Master of the Flag won the championship in 2009; Demon of Ignorance is an open-source project for Stratego and includes an AI robot; Asmodeus, Celsius, Celsius1.1, PeternLewis, and Vixen are programs submitted during a programming competition at an Australian university in 2012, with PeternLewis ultimately winning the competition.As shown in Table 1, DeepNash won the vast majority of games against these robots, even though it had not trained against any of them, only using self-play for training. Therefore, even achieving an exact Nash equilibrium does not guarantee that one will not lose. For example, in several matches where DeepNash lost to Celsius1.1, the latter adopted a high-risk gaming strategy, using high-level pieces early on to gain an advantage. Most of the time, this strategy did not work, but occasionally it resulted in victory.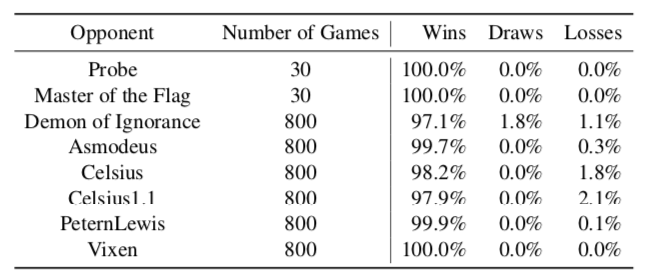Table 1: Evaluation of DeepNash against existing Stratego robots. These numbers are reported from DeepNash’s perspective. We conducted more matches against automated robots (800 matches). Except for matches against Master of the Flag, we played the same number of matches as both red and blue, while Master of the Flag played only as blue.

Double Line Title

3.3 Demonstration of DeepNash’s Capabilities

The sole objective of DeepNash during training is to learn the Nash equilibrium policy, and by doing so, it achieves the capabilities expected of a top player.In fact, the agent can utilize a variety of game situations, making it difficult for human players to defeat it by simply adjusting their deployments. We also demonstrate that DeepNash can make trade-offs between information and material, bluffing or betting when necessary. The remainder of this section will explain these behaviors through matches conducted on the Gravon platform.For convenience, we will explain DeepNash’s behavior in ways that human observers find natural (e.g., using terms like “deception” and “bluffing”). 3.3.1 Deploying PiecesIncomplete information in Stratego arises during the initial phase of the game. In this phase, both players secretly place their 40 pieces on the board. As mentioned, DeepNash simultaneously learns this deployment strategy in regular games, so both strategies develop together during learning. To avoid being defeated, it is crucial to conduct an unpredictable deployment. In fact, DeepNash can generate billions of unique deployment schemes. However, not all deployment schemes are equally strong (for example, placing the flag in an open front row is not advisable for obvious reasons). Figure 4a shows some deployment patterns that DeepNash frequently repeats.The flag is almost always placed in the back row and often protected by bombs. However, occasionally DeepNash does not surround the flag with bombs. Experts (e.g., Vincent de Boer, a three-time world champion) believe that occasionally not protecting the flag can be a good strategy, as this unpredictability increases difficulty for opponents towards the end of the game. Another pattern is that the highest-ranked pieces, number 9 and 10, are often deployed on different sides of the board. Additionally, spies are often positioned not far from the 9 (or 8) to protect them from the opponent’s 10. DeepNash does not frequently deploy bombs in the front row, which also aligns with human expert behavior. The three (miner) pieces that can dismantle bombs are often placed in the back row to expose more of the opponent’s bombs and potential flag locations, with their importance typically increasing during the game. The eight 2s (scouts) will be deployed in both the front and back rows, allowing for scouting the opponent’s pieces both at the beginning and the end of the game.3.3.2 Trade-offs Between Information and MaterialAn important tactic in Stratego is to hide as much information from the opponent as possible to gain an advantage. In certain game situations, players need to consider the trade-off between capturing an opponent’s piece (or even just moving a piece) and hiding the identity of their own pieces. DeepNash is capable of making these trade-offs excellently.Figure 4b illustrates a situation where DeepNash (blue) is behind in pieces (having lost a 7 and an 8) but ahead in information, as the red opponent has already revealed a 10, 9, an 8, and two 7s. Estimating the value of information and material in Stratego is unprecedented, but DeepNash has learned strategies through self-play that seem to naturally make this trade-off. In the above example, DeepNash is behind in material but knows the identities of many of the opponent’s high-ranking pieces. Conversely, almost all of DeepNash’s remaining pieces have not moved, while its opponent is in the dark. The value function (v = 0.403) considers this information asymmetry to be an advantage for DeepNash (with an expected win rate of about 70%), and despite having fewer pieces on the board, DeepNash still wins the game.The second example in Figure 4c shows that when DeepNash had the opportunity to capture the opponent’s 6 with its 9, it may have deemed that protecting the identity of the 9 was more important than the immediate gain. This situation also illustrates the randomness of DeepNash’s strategies during the game.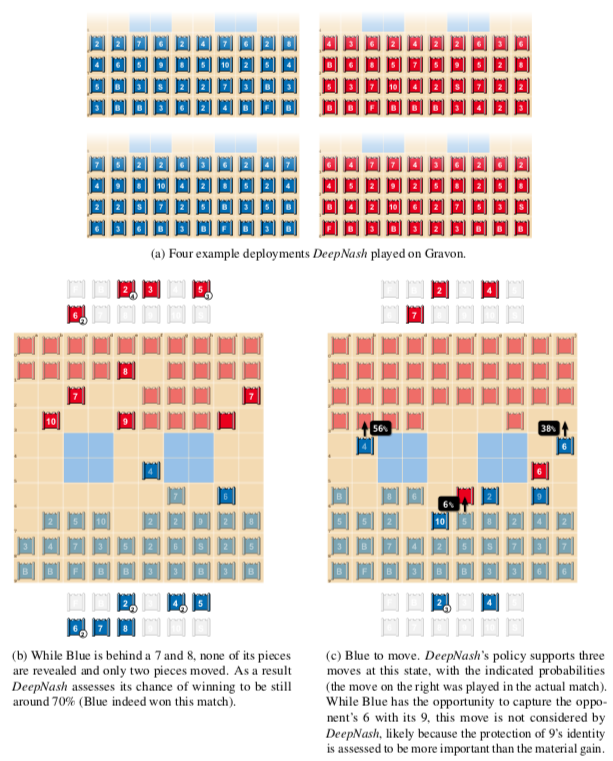Figure 4: DeepNash (blue) illustrates the assessment of the relative value of material and information against two human players (red).3.3.3 Deceptive Behaviors and BluffingThe agent occasionally bluffs to deceive opponents for an advantage. Figures 5a, 5b, and 5c illustrate this capability. Figure 5a shows an active bluff, where a player pretends that the value of a piece is higher than it actually is. DeepNash uses an unknown piece—scout 2—to pretend to be a 10, chasing the opponent’s 8. The opponent believes this piece is likely a 10, so they lure it next to their spy (which can capture a 10). However, while attempting to capture this piece, the opponent loses their spy to DeepNash’s scout.Figure 5b shows a passive bluff, where a player pretends that the value of a piece is lower than it actually is. DeepNash moves its unknown 10, which the opponent interprets as an active bluff. They assume DeepNash is moving a lower-ranked piece, possibly a spy, bringing it closer to the opponent’s 10, and thus try to capture it with their known 8. However, the opponent encounters DeepNash’s 10 and loses their 8.Figure 5c displays a more complex bluff, where DeepNash brings its undisclosed scout (2) close to the opponent’s 10, an action easily interpreted as a spy. This tactic actually allows the blue side to capture the red side’s 5 with its 7 in a few moves, gaining material. However, preventing the 5 from capturing the scout (2) reveals that it is not actually a spy.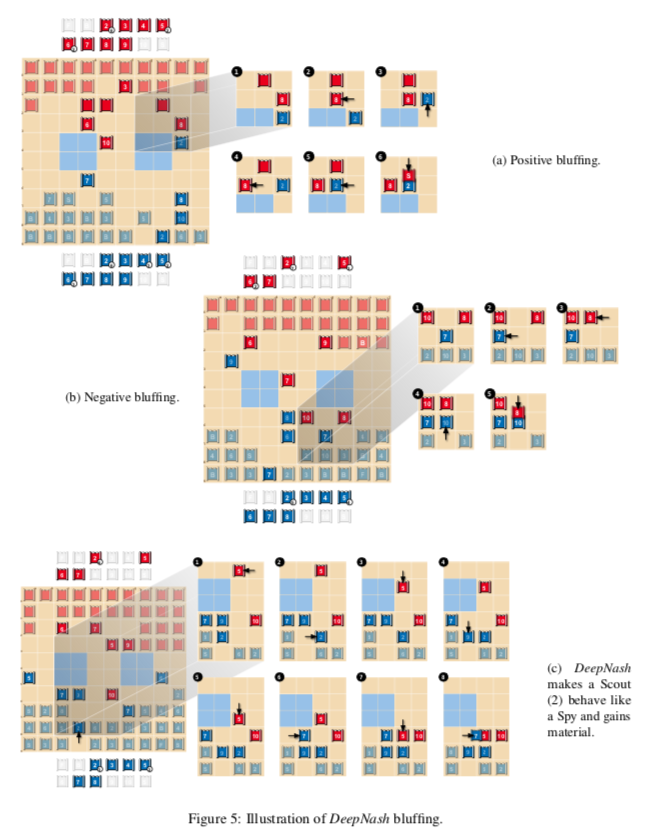Figure 5: Examples of DeepNash’s bluffing

4

Summary

In this article, we introduced a new method called DeepNash. It learns the incomplete information game Stratego from scratch through self-play until reaching human expert level.This model-free learning method does not perform any form of search or explicit opponent modeling, combining deep residual neural networks with the game-theoretic regularized Nash dynamics (R-NaD) multi-agent learning algorithm. Thus, DeepNash adopts an approach orthogonal to the current state-of-the-art model-based learning methods. It learns both the deployment of pieces at the start of the game and the actual game itself.The core behind DeepNash is the large-scale implementation of the R-NaD algorithm.DeepNash iteratively performs three fundamental steps: starting from a random regularized policy, performing reward transformation to define a modified game, then applying replicator dynamics on this modified game to converge to a fixed-point policy, and finally updating the regularized policy to this new fixed point. Repeating these three steps demonstrates the learning algorithm’s convergence to the 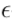-Nash equilibrium in Stratego.DeepNash has achieved remarkable results in matches against both state-of-the-art Stratego robots and human expert players.The Stratego community considers this achievement impossible with current technology. Since June 2021, we have been researching DeepNash with Vincent de Boer (a co-author of this paper), who has been a three-time Stratego world champion and currently ranks fourth in the official world rankings. Vincent has helped evaluate DeepNash, detecting weaknesses in each version and providing feedback for improvements to the agent.In summary, we believe DeepNash can open up further applications of RL methods in real-world multi-agent problems. These problems, with astronomical state spaces and incomplete information, cannot currently be addressed in an end-to-end manner with the most advanced AI methods.

References

1. C. E. Shannon, Philosophical Magazine 41, 256 (1950).

2. M. Campbell, A. J. Hoane Jr., F.-h. Hse, Artificial Intelligence 134, 57 (2002).

3. D. Silver, et al., Science 362, 1140 (2018).

4. J. Schrittwieser, et al., Nature 588, 604 (2020).

5. M. Moravcˇík, et al., Science 356, 508 (2017).

6. N. Brown, T. Sandholm, Science 359, 418 (2018).

7. N. Brown, T. Sandholm, Science 365, 885 (2019).

8. M. Schmid, et al., CoRR abs/2112.03178 (2021).

9. A. Arts, Competitive play in stratego, Ph.D. thesis, Maastricht University (2010).

10. M. Johanson, Measuring the size of large no-limit poker games (2013).

11. O. Vinyals, et al., Nature 575, 350 (2019).

12. M. Jaderberg, et al., Science 364, 859 (2019).

13. C. Berner, et al., arXiv preprint arXiv:1912.06680 (2019).

14. C. Treijtel, L. J. M. Rothkrantz, 2nd International Conference on Intelligent Games and Simulation (GAME-ON 2001), November 30 – December 1, 2001, London, UK, Q. H. Mehdi, N. E. Gough, eds. (2001), p. 17.

15. V. de Boer, Invincible: a stratego bot. MsC thesis (TU Delft, the Netherlands, 2007).

16. V. de Boer, L. J. M. Rothkrantz, P. Wiggers, Int. J. Intell. Games Simul. 5, 25 (2008).

17. M. Schadd, M. Winands, Proceedings of the Twenty-First Benelux Conference on Artificial

Intelligence (BNAIC 2009) (2009), pp. 225–232.

18. I. Satz, J. Int. Comput. Games Assoc. 34, 27 (2011).

19. S. Redeca, A. Groza, 2018 IEEE 14th International Conference on Intelligent Computer Communication and Processing (ICCP) (2018), pp. 97–104.

20. S. Mcaleer, J. Lanier, R. Fox, P. Baldi, Advances in Neural Information Processing Systems 33, 20238 (2020).

21. Official stratego rules, https://isfstratego.kleier.net/docs/rulreg/ isfgamerules.pdf. Accessed: 2021-11-

22. J. Nash, Annals of Mathematics 54, 286 (1951).

23. J. von Neumann, O. Morgenstern, Theory of games and economic behavior (Princeton

University Press, 1947).

24. Gravon, https://www.gravon.de/gravon/. Accessed: 2022-05-16.

25. M. Moravcík, et al., CoRR abs/1701.01724 (2017).

26. D. Silver, et al., Nat. 529, 484 (2016).

27. N. Brown, A. Bakhtin, A. Lerer, Q. Gong, Thirty-fourth Annual Conference on Neural Information Processing Systems (NeurIPS) (2020). https://arxiv.org/abs/2007. 13544.

28. O. Vinyals, et al., Nature 575, 350 (2019).

29. OpenAI, OpenAI Five, https://blog.openai.com/openai-five/ (2018).

30. E. Lockhart, et al., Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI-19 (International Joint Conferences on Artificial Intelligence Organization, 2019), pp. 464–470.

31. K. Tuyls, K. Verbeeck, T. Lenaerts, The Second International Joint Conference on Au- tonomous Agents & Multiagent Systems, AAMAS 2003, July 14-18, 2003, Melbourne, Victoria, Australia, Proceedings (2003), pp. 693–700.

32. K. Tuyls, P. J. Hoen, B. Vanschoenwinkel, Autonomous Agents and Multi-Agent Systems 12, 115 (2006).

33. K. Tuyls, D. Heytens, A. Nowé, B. Manderick, Machine Learning: ECML 2003, 14th European Conference on Machine Learning, Cavtat-Dubrovnik, Croatia, September 22-26, 2003, Proceedings, N. Lavrac, D. Gamberger, L. Todorovski, H. Blockeel, eds. (Springer, 2003), vol. 2837 of Lecture Notes in Computer Science, pp. 421–431.

34. J. Perolat, et al., International Conference on Machine Learning (2021).

35. G. Piliouras, L. J. Schulman, arXiv preprint arXiv:1711.06879 (2017).

36. P. Mertikopoulos, C. Papadimitriou, G. Piliouras, Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms (SIAM, 2018), pp. 2703–2717.

37. H. B. McMahan, Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, AISTATS 2011, Fort Lauderdale, USA, April 11-13, 2011, G. J. Gordon, D. B. Dunson, M. Dudík, eds. (JMLR.org, 2011), vol. 15 of JMLR Proceedings, pp. 525–533.

38. E. Zeeman, Lecture Notes in Mathematics, Global theory of dynamical systems 819 (1980).

39. E. Zeeman, Theoretical Biology 89, 249 (1981).

40. J. Maynard Smith, On Evolution (1972).

41. D. Bloembergen, K. Tuyls, D. Hennes, M. Kaisers, J. Artif. Intell. Res. 53, 659 (2015).

42. O. Ronneberger, P. Fischer, T. Brox, International Conference on Medical image computing and computer-assisted intervention (Springer, 2015), pp. 234–241.

43. K. He, X. Zhang, S. Ren, J. Sun, Proceedings of the IEEE conference on computer vision and pattern recognition (2016), pp. 770–778.

44. L. Espeholt, et al., International Conference on Machine Learning (2018), pp. 1406–1415.

45. D. Hennes, et al., Proceedings of the International Conference on Autonomous Agents and

Multiagent Systems (AAMAS) (2020).

46. Kleier rating system, https://www.kleier.net. Accessed: 2022-05-24.

47. Stratego on wikipedia, https://en.wikipedia.org/wiki/Stratego. Accessed: 2021-12-01.

48. Demon of Ignorance Stratego AI, https://github.com/braathwaate/ stratego. Accessed: 2021-12-01.

49. University Computer Club in Australia 2012 programming competition, https:// github.com/braathwaate/strategoevaluator. Accessed: 2021-12-13.

50. J. Hannan, Contributions to the Theory of Games 3, 97 (1957).

51. S. Hart, A. Mas-Colell, Econometrica 68, 1127 (2000).

52. Y. Freund, R. E. Schapire, Proceedings of the ninth annual conference on Computational learning theory (1996), pp. 325–332.

53. M. Zinkevich, M. Johanson, M. Bowling, C. Piccione, Advances in neural information processing systems (2008), pp. 1729–1736.

54. M. Lanctot, K. Waugh, M. Zinkevich, M. Bowling, Advances in neural information process- ing systems 22 (2009).

55. R. Gibson, Regret Minimization in Games and the Development of Champion Multiplayer Computer Poker-Playing Agents (University of Alberta, Canada, 2014).

56. O. Tammelin, N. Burch, M. Johanson, M. Bowling, Twenty-fourth international joint conference on artficial intelligence (2015).

57. N. Brown, T. Sandholm, Proceedings of the AAAI Conference on Artificial Intelligence (2019), pp. 1829–1836.

58. G. Tesauro, et al., Communications of the ACM 38, 58 (1995).

59. M. Buro, International Conference on Computers and Games (Springer, 1998), pp. 126–145.

60. J. Schaeffer, M. Hlynka, V. Jussila, International Joint Conference on Artificial intelligence (2001).

61. D. Silver, et al., Nature 550 (2017).

62. D. Silver, et al., Science 362 (2018).

63. N. Brown, A. Lerer, S. Gross, T. Sandholm, International Conference on Machine Learning (2019), pp. 793–802.

64. E. Steinberger, A. Lerer, N. Brown, arXiv preprint arXiv:2006.10410 (2020).

65. A. Gruslys, et al., arXiv preprint arXiv:2008.12234 (2020).

66. J. Heinrich, D. Silver, arXiv preprint arXiv:1603.01121 (2016).

67. M. Lanctot, et al., Advances in Neural Information Processing Systems (2017), pp. 4190– 4203.

68. C. Berner, et al., arXiv preprint arXiv:1912.06680 (2019).

69. M. Jaderberg, et al., Science 364, 859 (2019).

70. S. Srinivasan, et al., Advances in neural information processing systems (2018), pp. 3422– 3435.

71. S. Omidshafiei, et al., arXiv preprint arXiv:1906.00190 (2019).

72. M. Schadd, M. Winands, Proceedings of the 21st Benelux Conference on Artificial Intelli-

gence. Eindhoven, the Netherlands (2009).

73. S. Jug, M. Schadd, Icga Journal 32, 233 (2009).

74. J. Maynard Smith, Evolution and the Theory of Games. (Cambridge University Press, 1982).

75. T.-Y. Lin, et al., Proceedings of the IEEE conference on computer vision and pattern recognition (2017), pp. 2117–2125.

76. Y. LeCun, L. Bottou, Y. Bengio, P. Haffner, Proceedings of the IEEE 86, 2278 (1998).

77. J. Long, E. Shelhamer, T. Darrell, Proceedings of the IEEE conference on computer vision

and pattern recognition (2015), pp. 3431–3440.

78. M. Hessel, et al., Podracer architectures for scalable reinforcement learning (2021).

79. J. Bradbury, et al., JAX: composable transformations of Python+NumPy programs (2018).

80. M. Lanctot, et al., CoRR abs/1908.09453 (2019).

81. Master of the Flag, http://www.jayoogee.com/masteroftheflag/game. html. Accessed: 2022-05-16.

（References can be scrolled up and down to view）『Previous Highlights』▼▼▼

• DeepMind’s