On November 24, a paper titled “LLaMA-Berry: Pairwise Optimization for Olympiad-level Mathematical Reasoning via O1-like Monte Carlo Tree Search” was published by researchers from Fudan University, Shanghai AI Lab, UC Merced, Hong Kong Polytechnic, University of New South Wales, Shanghai Jiao Tong University, and Stanford University.
This paper proposes a mathematical reasoning framework called LLaMA-Berry to enhance the problem-solving capabilities of large language models (LLMs). The framework combines Monte Carlo Tree Search with Self-Refinement (SR-MCTS) to optimize reasoning paths and uses a pairwise reward model to evaluate different global paths. By leveraging the self-critique and rewriting capabilities of LLMs, SR-MCTS overcomes the inefficiencies and limitations of traditional stepwise reasoning and greedy search algorithms by facilitating a more effective exploration of the solution space. To guide the search process, a Pairwise Preference Reward Model (PPRM) is proposed, which predicts pairwise preferences between solutions using reinforcement learning from human feedback (RLHF) trained on instruction-following capabilities. Finally, an Enhanced Borda Count (EBC) method is employed to synthesize pairwise preferences into a global quantile score for evaluation. This approach addresses the challenges of score variability and non-independent distributions in mathematical reasoning tasks. The framework has been tested on general and advanced benchmarks, demonstrating good search efficiency and performance compared to existing open-source and closed-source methods, especially in complex Olympiad-level benchmarks such as AIME24 and AMC23.
Mathematical reasoning is a significant challenge in the field of artificial intelligence, widely applied in automated theorem proving, mathematical problem-solving, and scientific discovery (Ahn, 2024). Recently, large language models (LLMs) such as GPT-4 (Achiam, 2023) have made substantial progress in general mathematical tasks involving arithmetic and geometric problem-solving (Cobbe, 2021; Sun, 2024; Ying, 2024). However, complex mathematical reasoning remains challenging, particularly in Olympiad-level benchmarks like AIME (MAA, 2024).
An intuitive approach to enhancing problem-solving capabilities is to decompose solutions into stepwise reasoning paths (Lightman, 2023; Luo, 2024a), as demonstrated by Chain-of-Thought (CoT Wei, 2022). Although prompt-based methods can effectively facilitate the construction of such reasoning paths, they may still encounter challenges due to a lack of comprehensive feedback during the generation process, affecting efficiency (Paul, 2023). Another promising research direction, compared to stepwise generation methods, treats the entire solution as an independent state, using rewriting functions to improve solutions, such as Self-Refine (Madaan, 2023a) and Reflexion (Shinn, 2024). However, while these methods are innovative, they sometimes face challenges, such as getting stuck in local optima or potentially favoring suboptimal solutions due to feedback defects, which can impact their maximum potential performance.
In addition to generating reasoning paths, effective solution evaluation is also crucial, with models like the Outcome Reward Model (ORM) and Process Reward Model (PRM) (Uesato, 2022) being valuable examples. ORM focuses on the correctness of the final answer in the reasoning path, while PRM emphasizes the correctness of each step in the process. Although both methods enable reward models to assign scalar scores, obtaining reliable labeled data to train these reward models remains a significant challenge. Moreover, the scoring criteria for mathematical reasoning tasks can vary greatly, as each problem has unique characteristics. This variability complicates the scalability of reward models and hinders their ability to capture local preference relationships between solutions. Despite being trained using language models, these reward models have yet to fully leverage instruction-following capabilities, which may limit their effectiveness in handling more complex reasoning tasks (Zhang, 2024a).
The reward model for reasoning is essential. Reliable reward models (Kang, 2024; Wang, 2023; Havrilla, 2024; Lightman, 2023; Ma, 2023) can effectively distinguish between expected and unexpected responses, which is particularly important in complex reasoning. The Outcome Reward Model (ORM) is trained on the final results of reasoning paths. Since rewards are determined by the final answer, ORM may be affected by coarse supervision and misalignment issues. In contrast, the Process Reward Model (PRM) provides more interpretable stepwise reward signals and guides the model to follow CoT. Therefore, PRM is generally considered more effective (Lightman et al., 2023). However, the success of PRM relies on a large amount of manually annotated data (Luo, 2024a; Havrilla, 2024), which is time-consuming and still faces challenges of absolute reward score volatility.
Tree search reasoning has proven effective in improving the probability of finding the correct answer by sampling different reasoning paths (Brown, 2024). Self-consistency (Wang et al., 2022) samples a complete path each time, while tree search methods such as Tree of Thought (ToT) (Yao et al., 2023) and Monte Carlo Tree Search (MCTS) (Chen et al., 2024a,b; Luo et al., 2024b; Feng et al., 2023; Xie et al., 2024; Xu, 2023; Liu et al., 2023; Tian et al., 2024; Ding et al., 2023) expand multiple steps to optimize step answers and ultimately obtain the optimal solution. Additionally, self-optimization (Madaan et al., 2023a) methods have become a recent focus. Self-validation (Gero, 2023; Weng, 2022) and rStar (Qi, 2024) utilize the inherent capabilities of models to iteratively explore and refine answers. However, the performance of self-refinement is often limited by the model’s inherent capabilities, especially for small language models (SLMs) that exhibit significantly weaker self-refinement abilities (Madaan, 2023b). Zhang (2024b) proposed that enhancing the mathematical reasoning capabilities of LLMs can be achieved by treating the refinement process as a directed acyclic graph (DAG) through multi-agent collaboration.
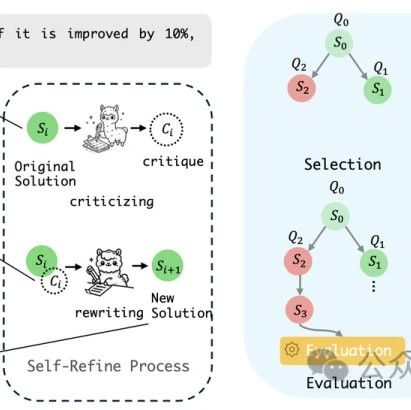
As shown, SR-MCTS combines Monte Carlo Tree Search (MCTS) with a self-optimization mechanism to continuously evaluate and optimize solution searches. This integration leverages the iterative nature of MCTS and the self-improvement capabilities of LLMs, thereby improving search results.
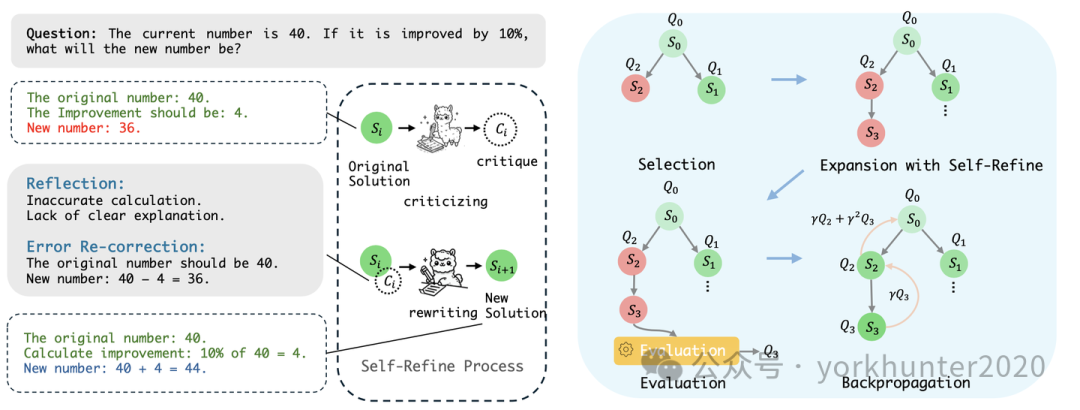
Monte Carlo Tree Search (MCTS) is an effective method within the Markov Decision Process (MDP) framework, sampling application states, actions, and value functions. The algorithm follows four key steps: Selection, Expansion, Evaluation, and Backpropagation. During the selection phase, the Upper Confidence Bound (UCB) algorithm is used to expand the root node, selecting nodes by balancing exploration and exploitation. In the expansion phase, node s generates subsequent state s′, adding it as a new node to the tree T. In the evaluation phase, these nodes’ Q values are typically estimated using simulation or heuristic methods. Finally, during backpropagation, the estimated Q values are updated from the leaf nodes back to the root node. This iterative process allows MCTS to improve decision-making by balancing the exploration of new paths and the exploitation of known high-value paths.
Selection Phase. The selection phase identifies a node s_i from the search tree T for expansion, where each node represents a complete solution state. The Upper Confidence Bound (UCB) algorithm is used to select the optimal node, employing dynamic pruning to avoid local optima. A node s_i is considered sufficiently explored when its child nodes reach a predefined limit, and at least one child’s Q value exceeds that of s_i.
Expansion Phase. In the expansion phase, as shown in the above figure, the selected answer s_i generates successor answers through a self-improvement process, which includes critique and rewriting processes. The critique process generates a critique c_i = C(s_i), pointing out flaws in the current selected answer S_i (such as mathematical errors or logical failures); the rewriting process generates a new answer s_i+1 = R(s_i, c_i). In practice, to simplify the problem, this process is assumed to be deterministic, ensuring that the same original state solution s_i always produces the same successor state solution s_i+1. The new state solution s′ is then added as a new node to the search tree T.
Evaluation Phase. The evaluation phase uses the Pairwise Preference Reward Model (PPRM) to calculate the value Q(s′) of the newly generated node s′. The evaluation includes two steps: global value assessment and local value assessment. The global value Q_g(s′) is determined by the quantile of s′ in the win-loss preference matrix M, reflecting the win-loss relationships between nodes. The local value Q_l(s′) is derived by comparing it with adjacent nodes in the search tree T. The total value Q(s′) is then calculated as a weighted combination of the global and local values: Q(s′) = αQ_g(s′) + (1 − α)Q_l(s′), where α controls the relative influence of each component.
Backpropagation Phase. During the backpropagation phase, the value Q(s′) of the new node is propagated back to its parent node s_i, updating the Q value of s_i to the discounted sum of its children’s Q values: Q(s_i) = (1 − γ)Q(s_i) + γQ(s′). The discount factor γ indicates the importance of future rewards. This iterative update mechanism ensures that the value of the parent node is continuously optimized, enhancing guidance for future selections.
Furthermore, to control the growth of the search tree, the SR-MCTS method limits the maximum number of expansions N_max. When this limit is reached, the search process terminates, thus preventing the tree from expanding indefinitely. The overall goal of SR-MCTS is to maximize the expected highest Q value of all existing nodes S, guiding towards the most optimal result s∗ and ensuring that the search process efficiently converges to high-quality solutions.
Reliable evaluation of different solutions plays a crucial role in mathematical problem-solving tasks, as it better estimates Q values, providing better guidance. Existing reward models typically evaluate solutions by giving absolute scores, such as the Process Reward Model (PRM Lightman, 2023) and the Outcome Reward Model (ORM Yu, 2023). However, score-based reward models may not fully leverage the instruction-following capabilities of LLMs or effectively handle variations in scoring criteria, especially when the differences between solutions are very subtle. To address this issue, the Pairwise Preference Reward Model (PPRM) is proposed, leveraging a comprehensive preference dataset containing numerous samples from PRM and ORM methods (Toshniwal, 2024; Lightman, 2023) to learn preference relationships between mathematical solutions.
For two solutions (a1 and a2) to a given mathematical problem, a1 ≻ a2 denotes that a1 is preferred over a2. PPRM uses pairwise ordering to predict their relative quality. In this method, a1 ≻ a2 is represented by the tokens of the LLM, and the token logits calculated by the LLM are used to estimate P(a1 ≻ a2 | φ).
Inspired by advancements in Language Interface Fine-Tuning (LIFT Dinh, 2022), the training process of PPRM is structured as a question-and-answer task to leverage the instruction-following capabilities of LLMs. The model’s task is to answer the following question: “For problem Q, is solution a1 better than solution a2?” As illustrated. To form a robust training objective, the predicted token label yˆ (“yes” or “no”) is evaluated alongside the ground truth label y using an indicator function I.
Finally, a pairwise preference dataset D containing millions of mathematical problem solution pairs is transformed into a dataset D′ suitable for the question-and-answer task. RLHF techniques are employed to train the model to enhance its performance in the pairwise preference prediction question-and-answer task. Subsequently, the Direct Preference Optimization (DPO Rafailov, 2024) method is used to maximize the objective argmax_φ E_P[I(yˆ, y)] to find the optimal P_φ.
Although PPRM allows direct comparison of the quality of two solutions, it is still necessary to convert these local preferences into a cohesive global ranking for a comprehensive evaluation of the answers. This transformation process can be formalized as the Global Optimal Ranking Aggregation (GORA) problem related to Learning to Rank (LtR) methods. Additionally, an Enhanced Borda Count (EBC) method based on the transitivity assumption of mathematical problem solutions is proposed, which combines the naive Borda count algorithm with the preference transitive closure calculated by the Floyd-Warshall algorithm (Warshall, 1962).
Local Preference Calculation. First, PPRM generates a preference matrix M for all n problem solutions, where M_i,j = 1 indicates that solution a_i is preferred over solution a_j, otherwise M_i,j = 0. As shown in the above figure, this matrix can be viewed as the adjacency matrix of a directed graph G = (V, E), where each solution a_i corresponds to a vertex v_i, and if M_i,j = 1, there exists an edge e = (v_i, v_j), indicating that solution a_i is preferred over a_j.
Transformation Closure. To simplify the problem, the transitivity assumption of mathematical solutions is adopted, meaning if v_i ≻ v_k and v_k ≻ v_j, then v_i ≻ v_j. Under this assumption, the transformation closure C of the preference matrix can be computed using the Floyd-Warshall algorithm. For example, if M_i,k = 1 and M_k,j = 1, then M_i,j = 1.
Borda Count-Based Global Ranking. Next, based on the transformation closure matrix C, the Enhanced Borda Count method is applied for global ranking. The Enhanced Borda Count determines the ranking of each node by calculating its out-degree, which corresponds to the number of nodes it defeats. For each node v_i, Borda(v_i) is defined as (C_i,j), as listed in the ranking nodes in the figure.
The higher the Borda count, the higher the ranking. However, in practice, cyclic preferences may lead to efficiency issues in the naive Borda count method. To further refine the ranking, a re-ranking phase is designed, where the pairwise preferences generated by PPRM are used for soft comparisons among nodes with equal Borda counts. Specifically, for two nodes v_i and v_j with equal Borda counts, the soft comparison rule can be expressed as v_i ≻v_j ⇐⇒ P(a_i ≻a_j) > P(a_j ≻a_i). This process ensures that even in the presence of cycles or local ambiguities, the ranking remains consistent and reasonable.
Global Quantile Score of Solutions. Finally, the ranking is converted into a global quantile score Q_g for each solution v, defined as Q_g(v) = 1 − (rank(v)−1)/( |V|−1), where rank(v) is the position of v in the Borda count ranking, and |V| is the total number of nodes. To reflect the local advantage in the structure of the search tree, the local winning rate Q_l(v) of node v and its children Children_v is calculated in C.
Ultimately, the score Q(v) of a solution is the weighted sum of the local winning rate Q_l(v) and the global quantile score Q_g.
To better evaluate the effectiveness of the method, the LLaMA-3.1-8B-Instruct model (Meta, 2024b) is chosen as the base model for SR-MCTS without any additional training. The Gemma2-2B-Instruct model (Google, 2024) is also trained as PPRM to provide reward signals during the search process. The Berry-Tree reasoning framework is developed to ensure robust and efficient reasoning, supporting advanced features such as fault tolerance, checkpoint recovery, multi-query concurrency, and automatic multi-server load balancing.
The design goal of PPRM is to integrate the properties of PRM and ORM, providing more detailed preference predictions for any two solution answers. Attempts to utilize reinforcement learning methods for training leverage the model’s instruction-following capabilities to predict the relative merits of pairs of problem-solving answers. This will further enable the EBC method to be used for evaluating the global quantile scores of mathematical solutions.
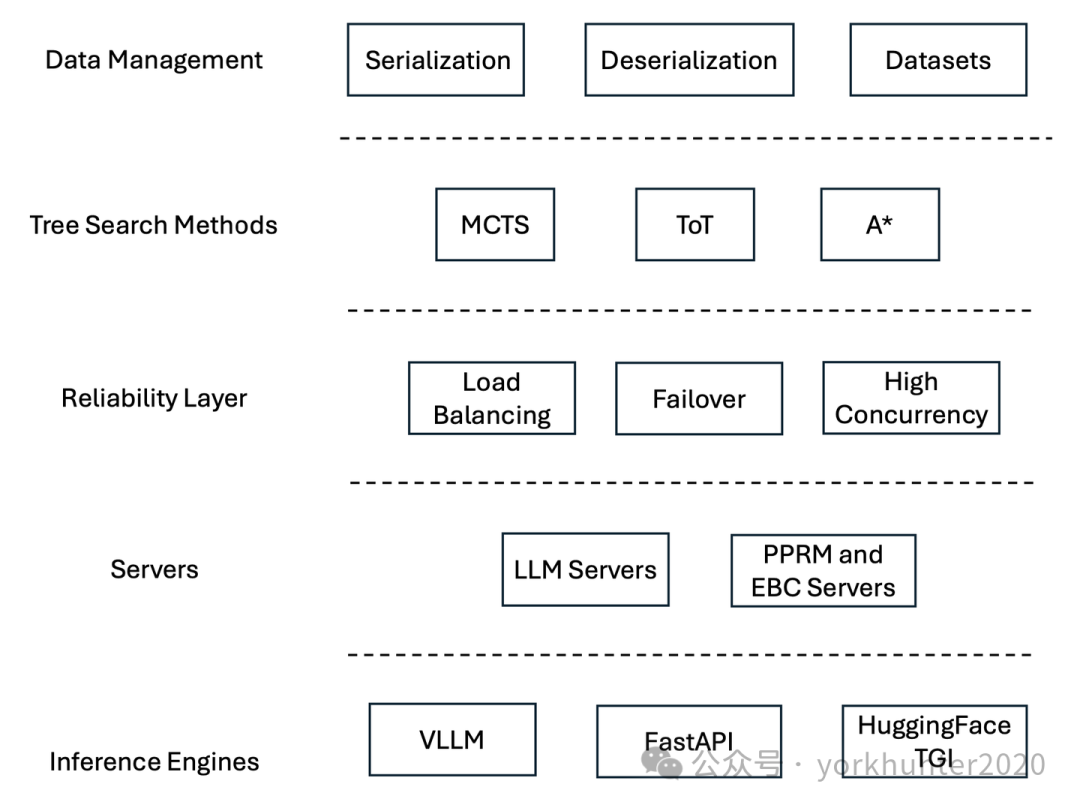
The Berry-Tree reasoning framework is specifically designed for complex multi-model reasoning tasks, addressing the need for improved reasoning efficiency and accuracy in the challenging tree search processes of LLMs. This framework is particularly suitable for large-scale reasoning tasks involving the integration of multiple models and algorithms. By combining advanced tree search methods, especially Monte Carlo Tree Search (MCTS), robust concurrent processing, and high-performance reasoning engines, Berry-Tree significantly enhances the reasoning speed and resource utilization of LLM mathematical reasoning processes.
As illustrated, the architecture of Berry-Tree is divided into several layers, each handling different functional requirements.The Data Management Layer is responsible for the serialization and deserialization of data, ensuring efficient read and write operations across models and systems, and enabling the recovery of the search process from serialized data.The Tree Search Methods Layer combines MCTS (Monte Carlo Tree Search), ToT (Tree of Thought), and the A* algorithm to optimize the reasoning process and explore multiple reasoning paths. Additionally, Berry-Tree includes a Reliability Layer, which ensures load balancing and fault tolerance support in high-concurrency scenarios, guaranteeing the stability of reasoning tasks. Finally, the Reasoning Engine Layer integrates efficient reasoning engines such as vLLM, FastAPI, and HuggingFace TGI, achieving parallel and efficient task processing.
Finally, the pseudocode of the algorithm presented in this paper is as follows: SR-MCTS and EBC.