Source: Machine Heart
This article is about 1600 words long, suggested reading time is 5 minutes.
Synthetic data continues to unlock the mathematical reasoning potential of large models!
The ability to solve mathematical problems has always been regarded as an important indicator of the intelligence level of language models. Typically, only models that are extremely large in scale or have undergone extensive pre-training related to mathematics have the opportunity to perform well on mathematical problems.
Recently, a research project named Xwin, developed by the Swin-Transformer team and scholars from Xi’an Jiaotong University, University of Science and Technology of China, Tsinghua University, and Microsoft Research Asia, has overturned this perception. It reveals that a 7B (i.e., 7 billion parameters) scale language model (LLaMA-2-7B) has already demonstrated strong potential in solving mathematical problems under general pre-training and can use a supervised fine-tuning method based on synthetic data to increasingly stabilize the model’s mathematical capabilities.
This research was published on arXiv, titled “Common 7B Language Models Already Possess Strong Math Capabilities”.
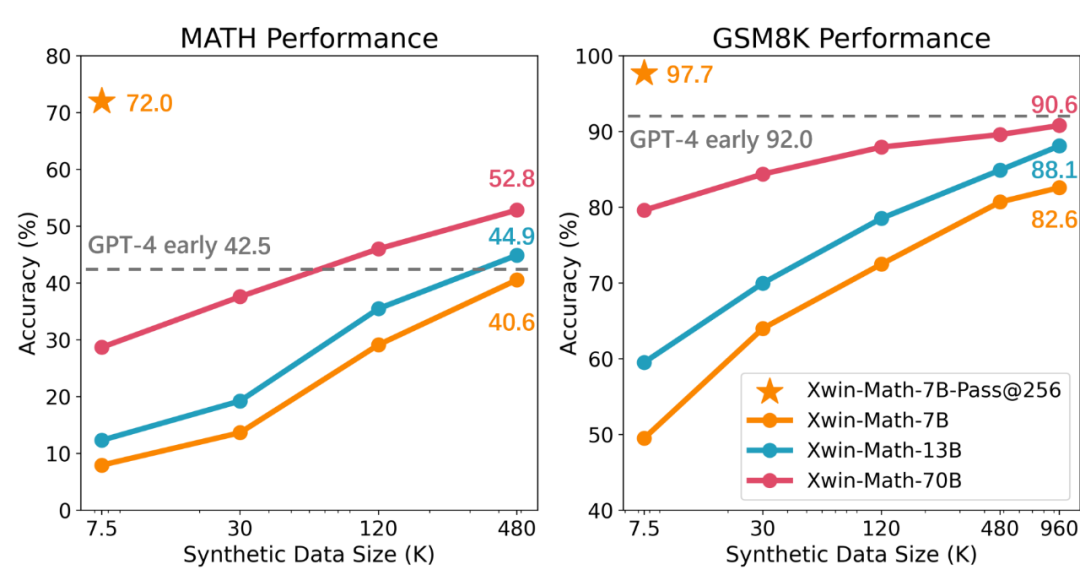
The research team first used only 7.5K data to fine-tune the LLaMA-2-7B model’s instructions and then evaluated the model’s performance on GSM8K and MATH. The experimental results show that when selecting the best answer from 256 generated answers for each question in the test set, the accuracy rates can reach as high as 97.7% and 72.0%, respectively. This result indicates that even a small model of 7B scale under general pre-training has enormous potential for generating high-quality answers, challenging the previous viewpoint that strong mathematical reasoning potential is limited to large-scale and mathematics-related pre-trained models.
 However, the research also points out that despite possessing strong mathematical reasoning potential, the main issue with current language models is their difficulty in consistently activating their intrinsic mathematical abilities. For example, in the previous experiments, if only one generated answer for each question is considered, the accuracy rates on the GSM8K and MATH benchmark tests drop to 49.5% and 7.9%, respectively. This reflects the instability of the model’s mathematical abilities. To address this issue, the research team adopted a method to expand the supervised fine-tuning (SFT) dataset and found that as the SFT data increased, the reliability of the model in generating correct answers was significantly improved.
The study also mentioned that by using synthetic data, the SFT dataset can be effectively expanded, and this method is nearly as effective as real data. The research team utilized the GPT-4 Turbo API to generate synthetic mathematical problems and solutions, ensuring the quality of the problems through simple validation prompts. Through this method, the team successfully expanded the SFT dataset from 7.5K to about one million samples, achieving an almost perfect scaling law. The final Xwin-Math-7B model achieved accuracy rates of 82.6% and 40.6% on GSM8K and MATH, respectively, significantly surpassing previous SOTA models, and even outperformed some 70B scale models, achieving a leap in performance. The Xwin-Math-70B model achieved results of 52.8% on the MATH evaluation set, significantly surpassing early versions of GPT-4. This is the first time research based on the LLaMA series foundational models has surpassed GPT-4 on MATH.
However, the research also points out that despite possessing strong mathematical reasoning potential, the main issue with current language models is their difficulty in consistently activating their intrinsic mathematical abilities. For example, in the previous experiments, if only one generated answer for each question is considered, the accuracy rates on the GSM8K and MATH benchmark tests drop to 49.5% and 7.9%, respectively. This reflects the instability of the model’s mathematical abilities. To address this issue, the research team adopted a method to expand the supervised fine-tuning (SFT) dataset and found that as the SFT data increased, the reliability of the model in generating correct answers was significantly improved.
The study also mentioned that by using synthetic data, the SFT dataset can be effectively expanded, and this method is nearly as effective as real data. The research team utilized the GPT-4 Turbo API to generate synthetic mathematical problems and solutions, ensuring the quality of the problems through simple validation prompts. Through this method, the team successfully expanded the SFT dataset from 7.5K to about one million samples, achieving an almost perfect scaling law. The final Xwin-Math-7B model achieved accuracy rates of 82.6% and 40.6% on GSM8K and MATH, respectively, significantly surpassing previous SOTA models, and even outperformed some 70B scale models, achieving a leap in performance. The Xwin-Math-70B model achieved results of 52.8% on the MATH evaluation set, significantly surpassing early versions of GPT-4. This is the first time research based on the LLaMA series foundational models has surpassed GPT-4 on MATH.
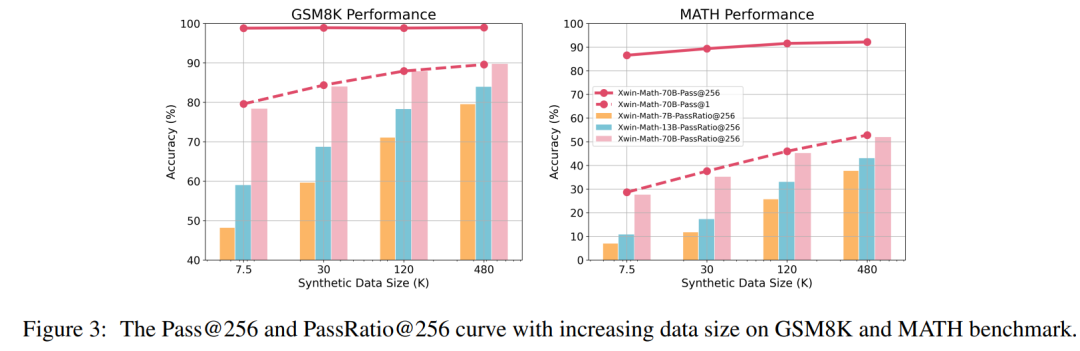
 The researchers also defined the evaluation metrics Pass@N and PassRatio@N, intending to measure whether the model can output correct answers in its N outputs (indicating the model’s potential mathematical abilities) and the proportion of correct answers (indicating the stability of the model’s mathematical abilities). When the SFT data volume is small, the model’s Pass@256 is already very high, and further expanding the SFT data scale results in minimal improvement in Pass@256, while PassRatio@256 experiences significant growth. This indicates that supervised fine-tuning based on synthetic data is an effective way to enhance the stability of the model’s mathematical abilities.
The researchers also defined the evaluation metrics Pass@N and PassRatio@N, intending to measure whether the model can output correct answers in its N outputs (indicating the model’s potential mathematical abilities) and the proportion of correct answers (indicating the stability of the model’s mathematical abilities). When the SFT data volume is small, the model’s Pass@256 is already very high, and further expanding the SFT data scale results in minimal improvement in Pass@256, while PassRatio@256 experiences significant growth. This indicates that supervised fine-tuning based on synthetic data is an effective way to enhance the stability of the model’s mathematical abilities.
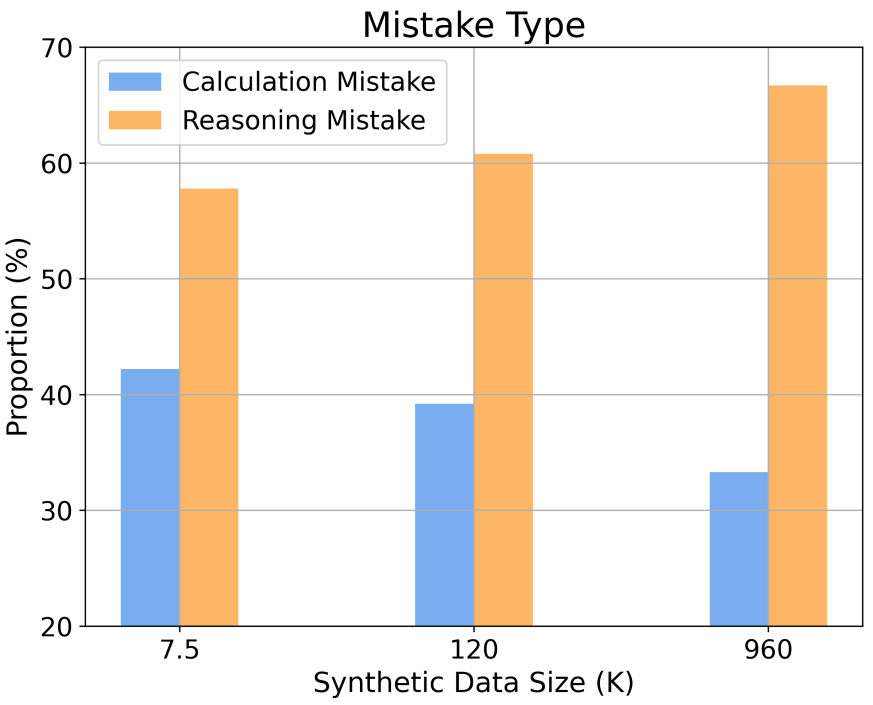
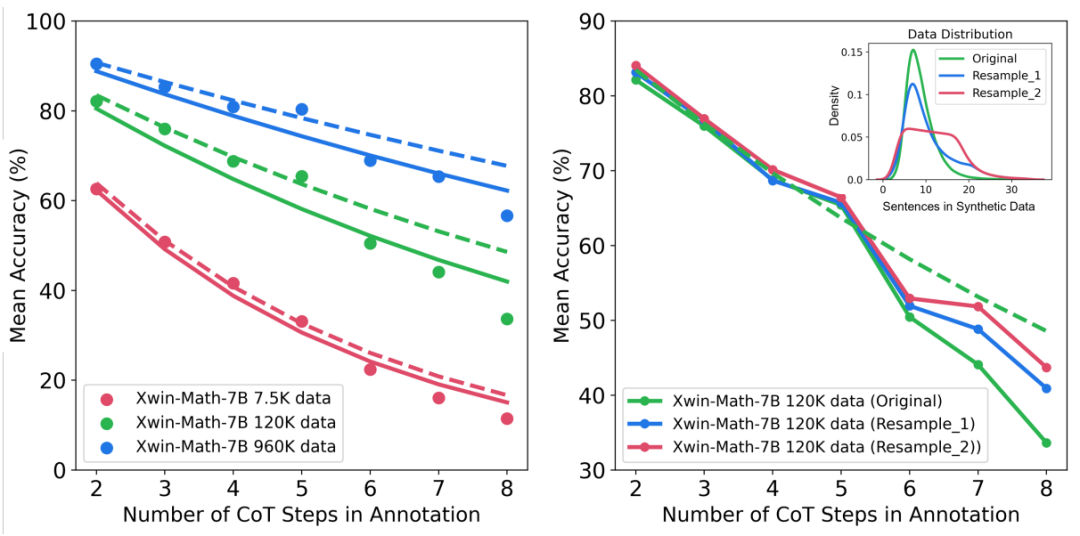
 Additionally, the research provides insights into the scaling behavior under different reasoning complexities and error types. For example, as the SFT dataset scale increases, the model’s accuracy in solving mathematical problems follows a power-law relationship related to the number of reasoning steps. By increasing the proportion of long reasoning steps in the training samples, the model’s accuracy in solving difficult problems can be significantly improved. At the same time, the research also found that computational errors are easier to mitigate than reasoning errors.
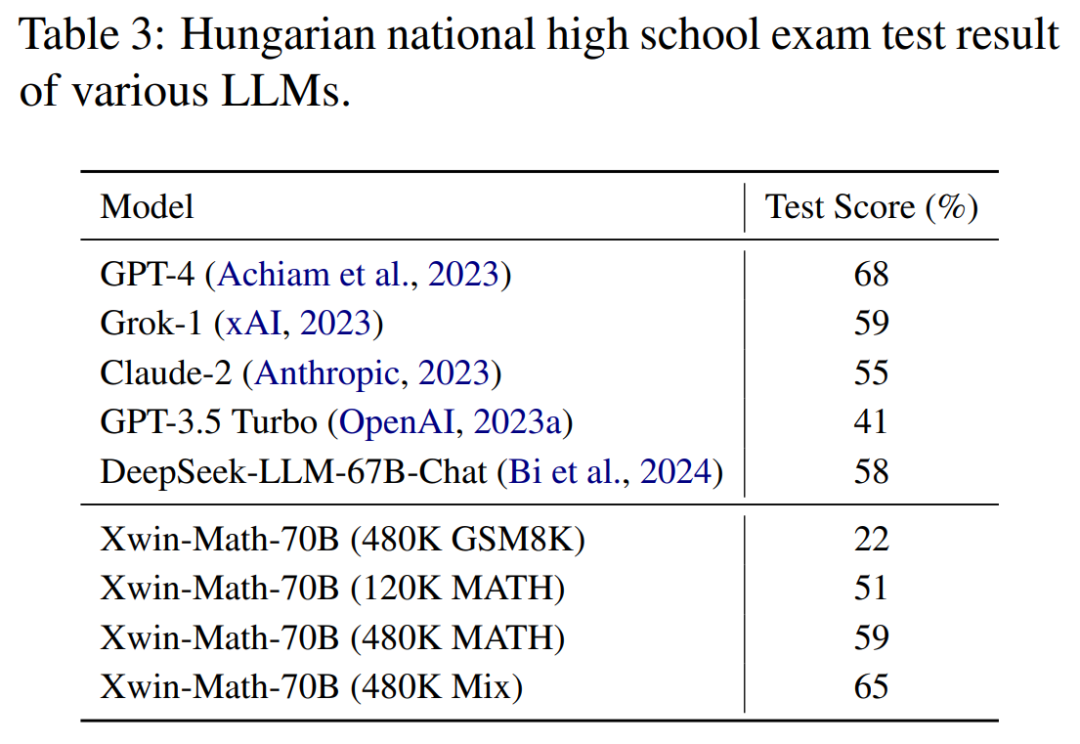
In the Hungarian high school mathematics exam that demonstrates the model’s mathematical reasoning generalization ability, Xwin-Math scored 65%, second only to GPT-4. This indicates that the synthetic data approach in the research did not significantly overfit to the evaluation set, demonstrating good generalization ability.
This research not only showcases the effectiveness of synthetic data in expanding the SFT dataset but also provides a new perspective for studying large language models’ mathematical reasoning abilities. The research team stated that their work lays the foundation for future exploration and advancements in this field and looks forward to promoting greater breakthroughs in AI’s ability to solve mathematical problems. With the continuous advancement of artificial intelligence technology, we have reason to expect that AI’s performance in mathematics will be even better, providing more help to humanity in solving complex mathematical problems.
The article also involves ablation experiments on data synthesis methods and results of other evaluation metrics; for detailed content, please refer to the full text.
Additionally, the research provides insights into the scaling behavior under different reasoning complexities and error types. For example, as the SFT dataset scale increases, the model’s accuracy in solving mathematical problems follows a power-law relationship related to the number of reasoning steps. By increasing the proportion of long reasoning steps in the training samples, the model’s accuracy in solving difficult problems can be significantly improved. At the same time, the research also found that computational errors are easier to mitigate than reasoning errors.
In the Hungarian high school mathematics exam that demonstrates the model’s mathematical reasoning generalization ability, Xwin-Math scored 65%, second only to GPT-4. This indicates that the synthetic data approach in the research did not significantly overfit to the evaluation set, demonstrating good generalization ability.
This research not only showcases the effectiveness of synthetic data in expanding the SFT dataset but also provides a new perspective for studying large language models’ mathematical reasoning abilities. The research team stated that their work lays the foundation for future exploration and advancements in this field and looks forward to promoting greater breakthroughs in AI’s ability to solve mathematical problems. With the continuous advancement of artificial intelligence technology, we have reason to expect that AI’s performance in mathematics will be even better, providing more help to humanity in solving complex mathematical problems.
The article also involves ablation experiments on data synthesis methods and results of other evaluation metrics; for detailed content, please refer to the full text.
Editor: Wen Jing