Follow the official account “ML_NLP“

Set as “Starred“, heavy content delivered first time!

As a major part of deep learning, model architecture has always been a hot topic of research. Besides AutoML technology, what are some unconventional and innovative network architectures?

1

Author: Yan You San Source: https://www.zhihu.com/question/337470480/answer/766380855This article has been authorized for reprint by the author, and unauthorized secondary reproduction is prohibited.

You are probably already familiar with basic convolution structures, well-versed in residual networks, and thoroughly understand grouped convolutions, and you also know some techniques for model compression. However, most of what we will discuss today may not be known to many students.

We won’t discuss popular model structures today; instead, we will introduce several models from various aspects such as convolution methods, channel changes, and topological structures. Students who aspire to publish papers in this direction should pay close attention.

1 Gradual Width – Pyramidal Structure

This is a network structure related to the variation of the number of channels.

Generally speaking, the variation in the number of channels in network structures is abrupt. Is there a network that increases gradually? This is the pyramidal structure, named Pyramidal Residual Networks.

Everyone knows that structures like CNN typically increase the number of channels in feature maps when the scale of the feature maps decreases to enhance the expressive ability of higher layers, which is crucial for model performance. Most models increase the number of channels in feature maps abruptly, such as jumping from 128 to 256.

We previously discussed that randomly deleting depths in residual networks proved that the depth of deep residual networks is not as deep as imagined. Research in the paper “Residual networks behave like ensembles of relatively shallow networks[C]” also indicated that removing some blocks does not significantly reduce performance, except for down-sampling network layers.

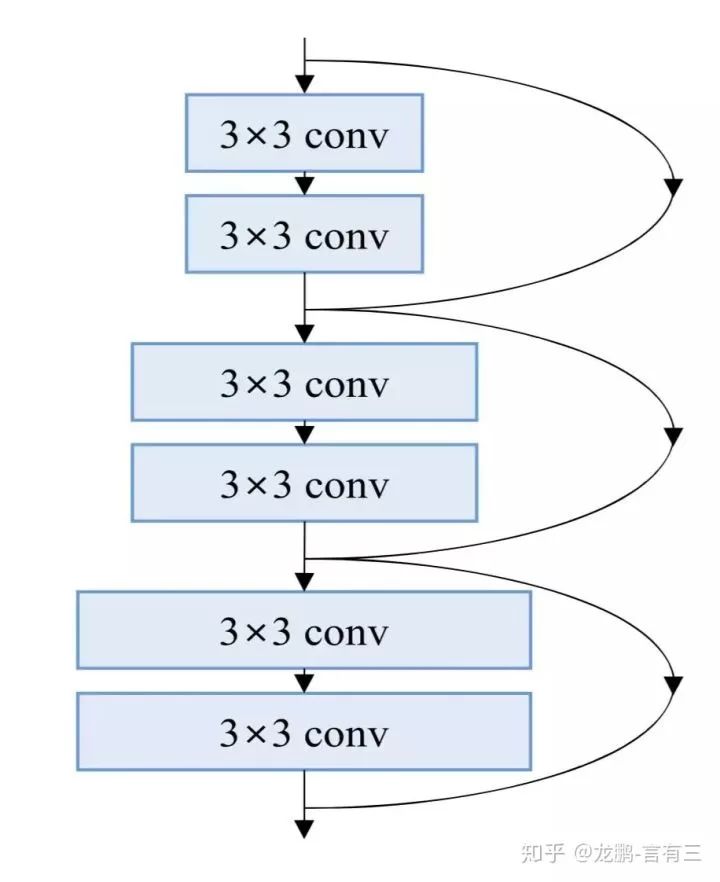
Based on this phenomenon, this article posits that to reduce the sensitivity of down-sampling, the variation in channels must be gradual, meaning that with the increase of layers, each layer gradually increases in width, thus naming it the pyramidal structure, as shown below.

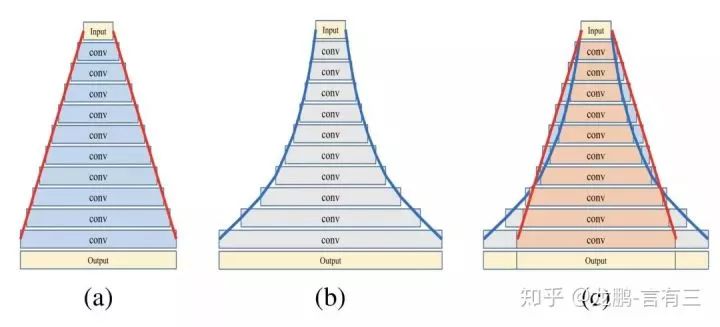
Here, figure a shows linear increase, while figure b shows exponential increase.

So how does performance measure up? First, let’s look at the comparison of training curves:

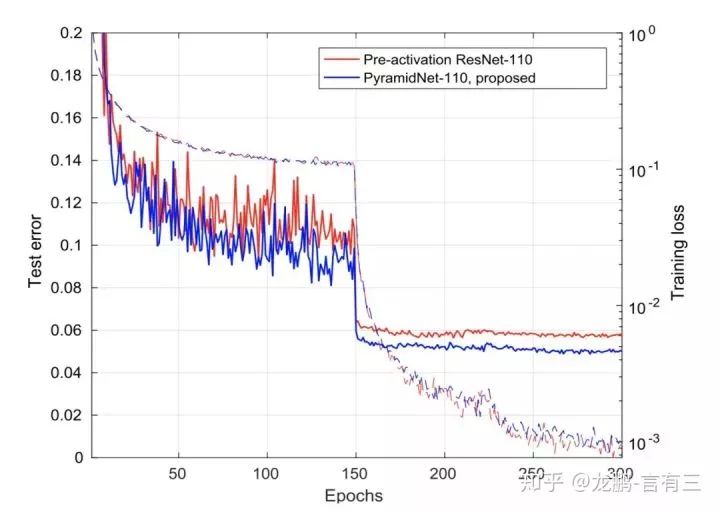
Both networks have similar parameters, around 1.7M, and from the curves, performance is also comparable.

Another issue to focus on is whether the Pyramidal ResNet achieves its original intention of improving the performance drop when down-sampling network layers are removed. The results are as follows:

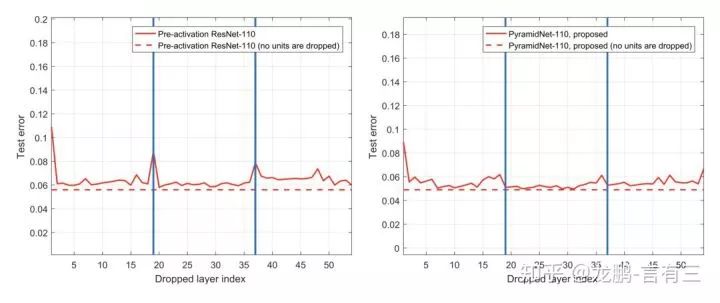
From the results, the error rate has indeed decreased. For more specific experimental results, feel free to check the paper yourself.

[1] Han D, Kim J, Kim J. Deep pyramidal residual networks[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2017: 5927-5935.

2 Many Branches – Fractal Structure

This is a network structure related to multi-branch architecture.

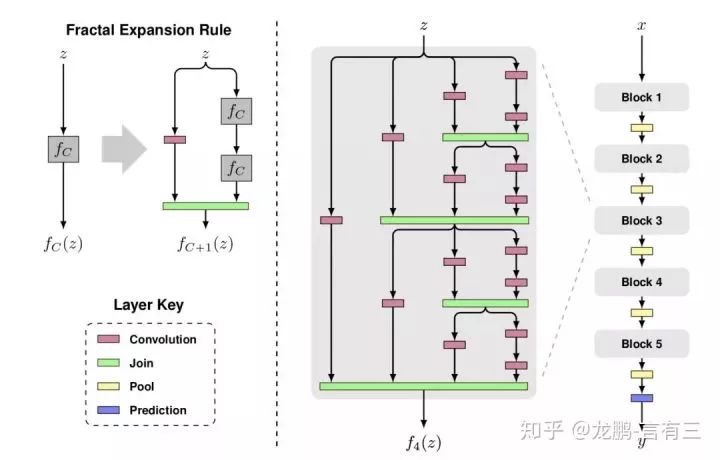
Residual networks enable the design of network structures with thousands of layers, but it is not only residual networks that can achieve this; FractalNet (Fractal Network) does as well.

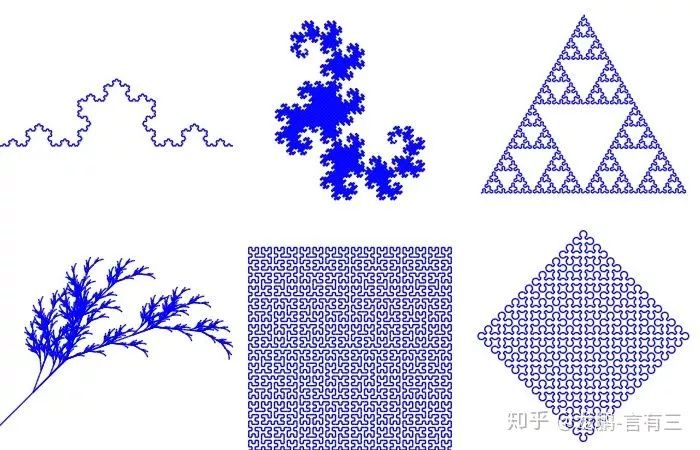
Fractals are a mathematical concept that refers to shapes with characteristics that fill space in non-integer dimensions, meaning their effective dimension is not an integer. However, we don’t need to focus on its mathematical definition here; rather, we should focus on its self-similar structure, which resembles the overall structure, as shown in the following figure:

Fractal networks, as the name suggests, also have this characteristic; the local structure resembles the global structure, as shown in the following figure:

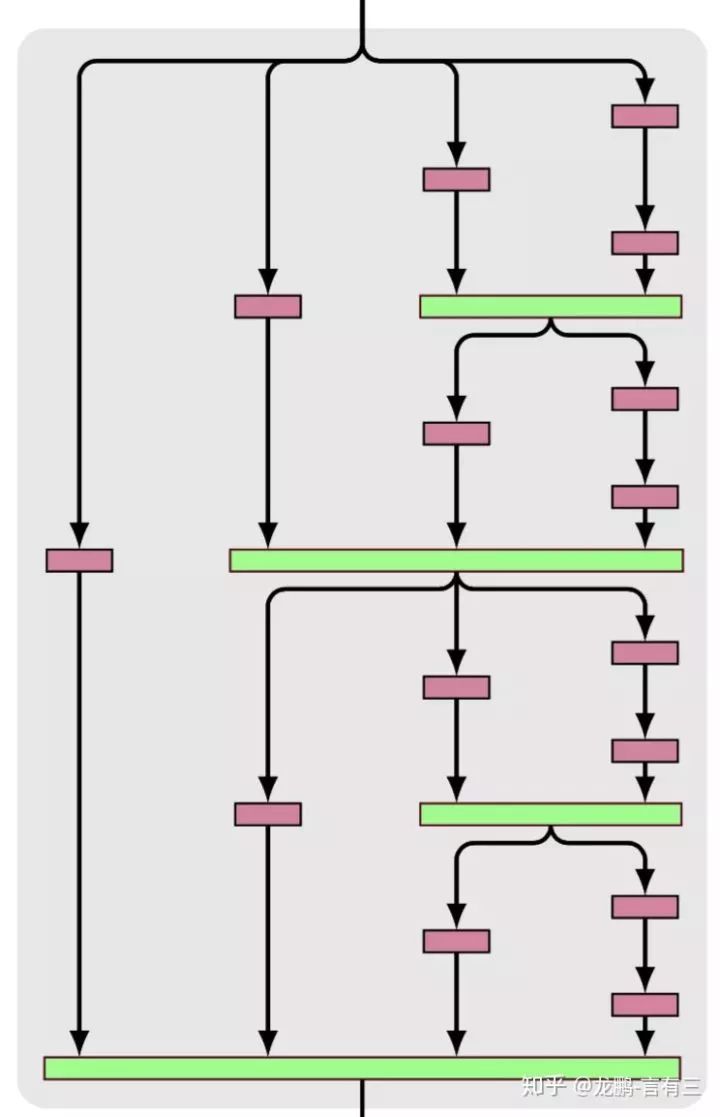
It can be seen that it contains various sub-paths of different lengths, from left to right:

The first column has only one path, length l.

The second column has two paths, each of length l/2.

The third column has four paths, each of length l/4.

The fourth column has eight paths, each of length l/8.

Its difference from residual networks is that the green modules represent nonlinear transformations, meaning that the next layer cannot directly receive signals from the previous layer; instead, they undergo transformations.

This kind of subnetwork containing different depths is reminiscent of stochastic depth mentioned earlier; it can also be viewed as an ensemble of networks with different depths.

The authors conducted experiments by randomly dropping certain depths, as shown in the following samples:

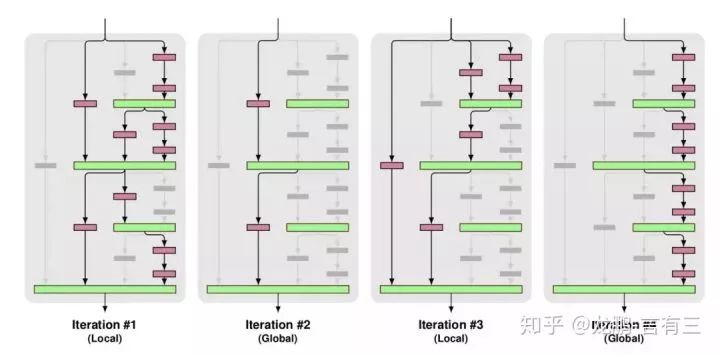
The above shows two types of paths used in training.

Global: Only one path is selected, and it is from the same column; this path is an independent strong prediction path.

Local: Contains multiple paths, but ensures that each layer has at least one input.

So what are the results?

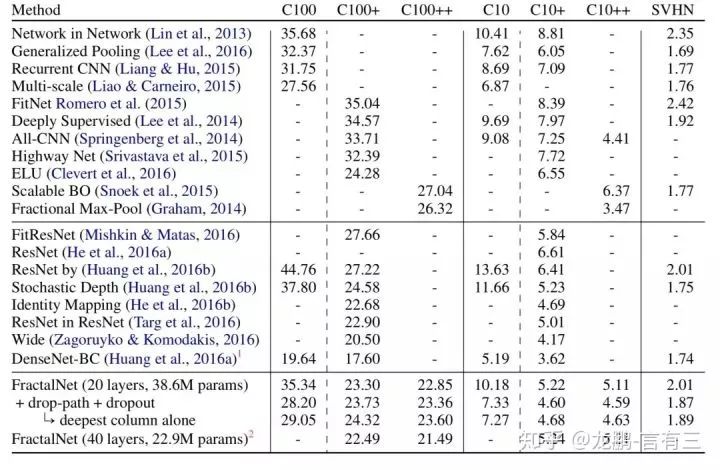
As shown above, compared with various networks, performance is excellent. After adding drop-path technology, there is significant improvement, and even networks derived from the deepest path have performance close to the best models.

Similar to research on residual networks, studies on fractal networks also demonstrate that the effective length of the path is the real influencing factor for training deep networks. Both fractal networks and residual networks have shorter effective gradient propagation paths, making it easier to train deep networks without overfitting.

[1] Larsson G, Maire M, Shakhnarovich G. Fractalnet: Ultra-deep neural networks without residuals[J]. arXiv preprint arXiv:1605.07648, 2016.

3 Everything Connects – Circular Network

This is a complex topological network structure based on skip connections.

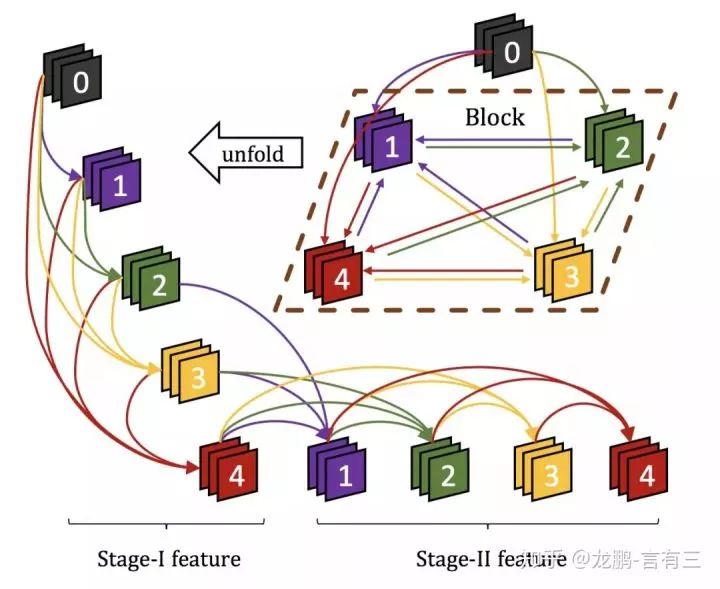
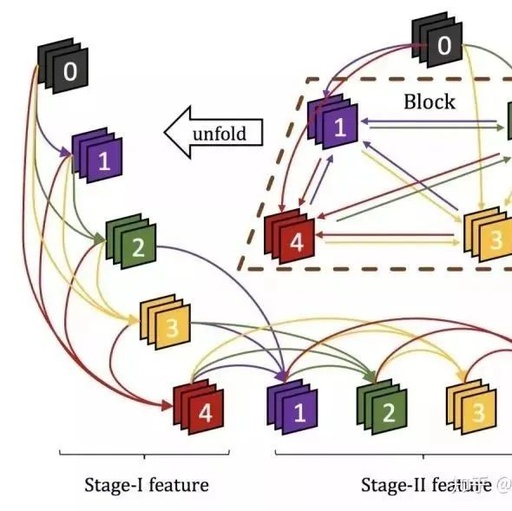
DenseNet improves channel utilization by reusing feature maps from different levels, but its connections are forward, meaning information can only be transmitted from shallow to deep layers, whereas CliqueNet goes a step further, allowing for bidirectional information transmission.

The structure is shown in the above figure; CliqueNet not only has a forward propagation part but also a backward propagation part. This network architecture is inspired by RNNs and attention mechanisms, allowing for more refined reuse of feature maps.

The training of CliqueNet consists of two stages. The first stage is similar to DenseNet, as shown in Stage-1 of the figure, where shallow features are transmitted to deep layers, which can be seen as an initialization process.

In the second stage, each layer not only receives feature maps from all previous layers but also receives feedback from subsequent layers. It can be seen that this is a cyclic feedback structure that utilizes higher-level visual information to refine the features from previous layers, achieving spatial attention effects. Experimental results show that it effectively suppresses background and noise activation.

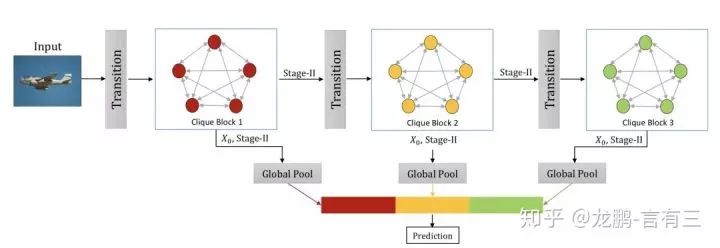
The overall network architecture is shown above: the network consists of many blocks, and the features from stage II of each block are connected through global pooling to generate the final features. Unlike DenseNet, with the network architecture, the input and output feature maps of each block do not need to increase, making it more efficient. The results are as follows:

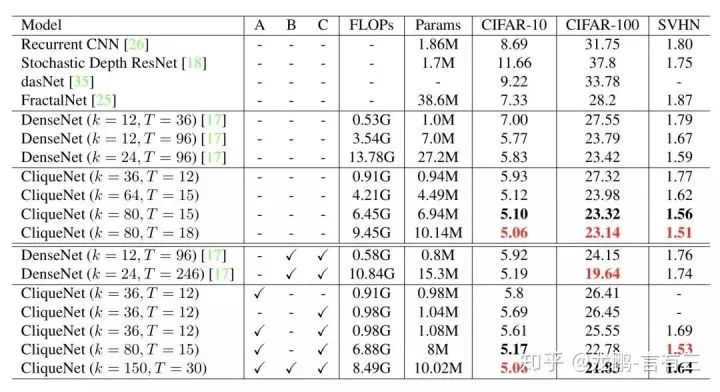
From the table above, it can be seen that the parameter count and accuracy are very advantageous.

[1] Yang Y, Zhong Z, Shen T, et al. Convolutional neural networks with alternately updated clique[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018: 2413-2422.

4 Irregular Convolution Kernels – Deformable Networks

This is a network structure related to the shape of convolution kernels.

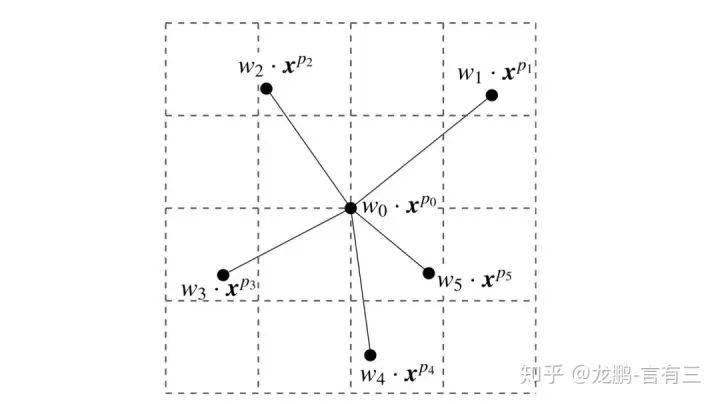
The convolution operation itself has a very fixed geometric structure; the standard convolution operation is a very regular sampling, usually square. If the convolution kernel uses non-regular sampling, meaning its shape is no longer standard square but arbitrary, it is called deformable convolution (Deformable Convolution).

To describe the convolution kernel above, not only weight coefficients are needed, but also offsets for each point. The idea of deformable convolution was first proposed in the form of Active Convolution.

In Active Convolution, each component of the convolution kernel has its own offset. For a 3*3 convolution, it includes 18 coefficients, with 9 offsets each in the X and Y directions. However, each channel shares these coefficients, so it is independent of the input and output channel counts.

For an input channel of M and an output channel of N using a 3*3 convolution in Active Convolution, the weight parameter count is M*N*3*3, and the offset parameter count is 2*3*3, which is negligible compared to the weight parameter count.

In Deformable Convolutional Networks, each channel does not share offsets, resulting in an offset parameter count of 2*M*3*3. The increased parameter count is more than that of Active Convolution, but compared to the weight parameter count of M*N*3*3, it is still much smaller, so it does not significantly increase the model size. Moreover, during actual implementation, output channels can be grouped.

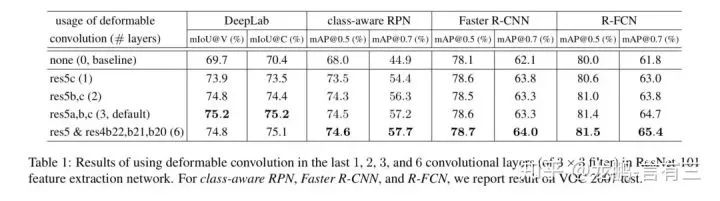
As shown in the above image, deformable convolution has a more flexible receptive field.

The implementation of deformable convolution only requires learning the offsets, which essentially adds an offset layer. We can also group the output to control the types of deformations to learn.

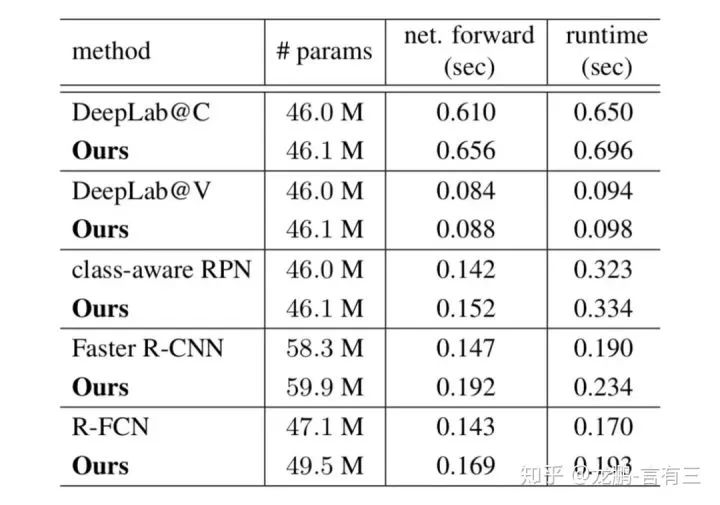
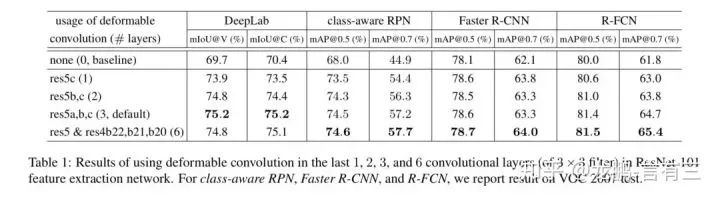
Finally, let’s look at the parameter comparisons and performance.

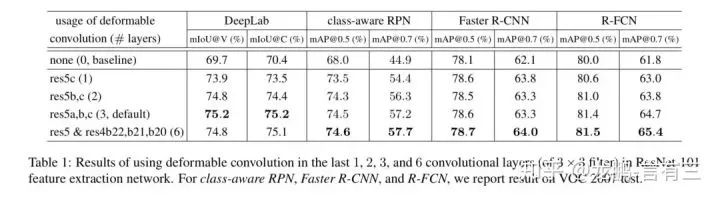
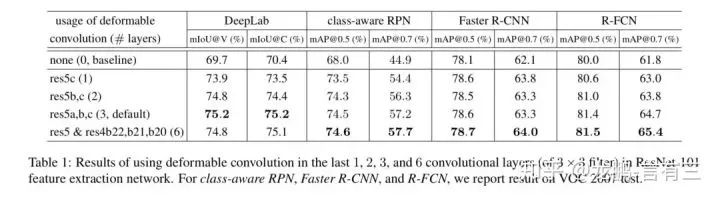
Experiments on various network layers show that the increase in parameter count is minimal, and performance is also enhanced. For specific effects, feel free to verify with your own experimental results.

[1] Jeon Y, Kim J. Active Convolution: Learning the Shape of Convolution for Image Classification[J]. 2017.[2] Dai J, Qi H, Xiong Y, et al. Deformable Convolutional Networks[J]. 2017.

5 Testing Variable Networks – Branching Networks

This is a network structure that dynamically changes during inference.

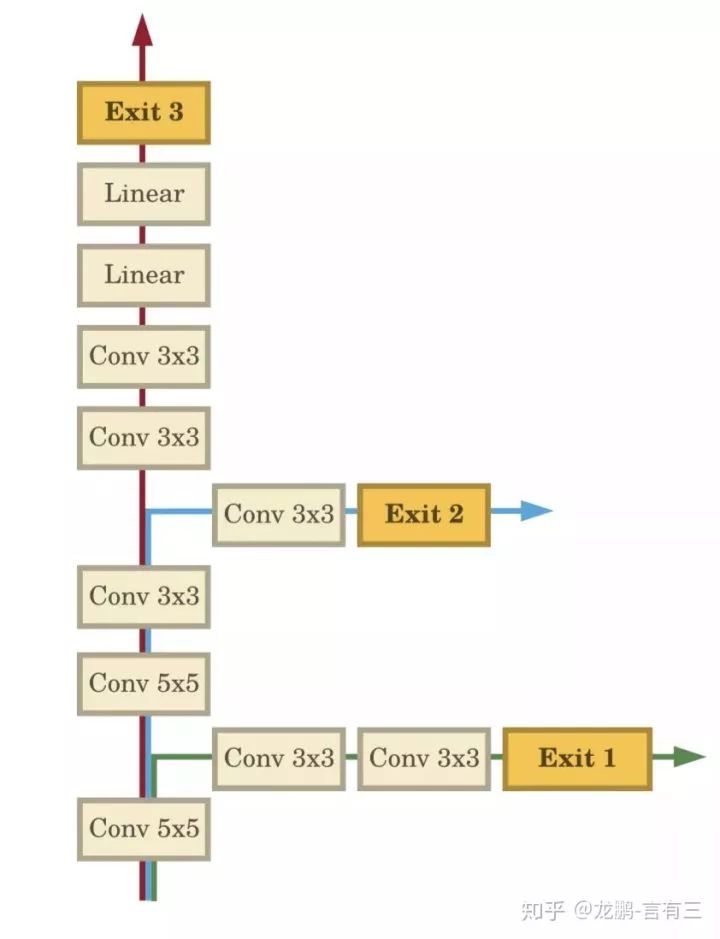
Typically, after training, the model structure is fixed, and during testing, images are computed along a fixed path. However, test samples can vary in difficulty; simple samples require minimal computation to complete the task, while difficult samples require more computation.

As shown in the above figure, it includes multiple bypass branches on the normal network path. This idea is based on the observation that as the network deepens, the representation ability increases, allowing most simple images to learn sufficient features for recognition at shallower layers, such as the Exit 1 channel in the figure. Some harder samples require further learning, as shown in the Exit 2 channel, while only a few samples require the entire network, as in the Exit 3 channel. This idea can achieve a balance between accuracy and computational load; for most samples, tasks can be completed with less computation.

So how do we determine if we can exit early? In the paper proposing this network, the authors used classification information entropy. Once the classification information entropy of a channel falls below a certain threshold, it indicates that a classification result has been obtained with high confidence, leading to an exit from the final channel.

During training, each channel contributes to the loss, with weights closer to the shallow layers being larger. The multi-channel loss not only enhances gradient information but also serves as a form of regularization.

Applying the design concept of BranchyNet to LeNet, AlexNet, and ResNet architectures resulted in noticeable acceleration while maintaining performance.

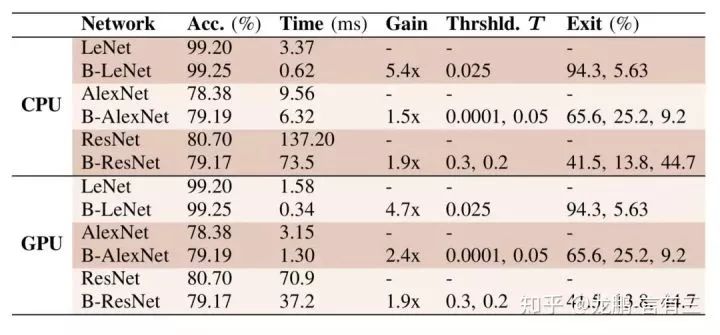
For a network with N branches, N-1 thresholds are needed, as the last branch does not require a threshold.

The LeNet series networks can allow over 90% of samples to terminate early at the first branch, while AlexNet and ResNet allow early termination for over half and over 40% of samples, respectively.

[1] Teerapittayanon S, McDanel B, Kung H T. Branchynet: Fast inference via early exiting from deep neural networks[C]//2016 23rd International Conference on Pattern Recognition (ICPR). IEEE, 2016: 2464-2469.

2

Author: People’s Artist Source: https://www.zhihu.com/question/337470480/answer/824132026This article is for learning reference only; copyright belongs to the author. If there is any infringement, please contact for deletion.

• Summary

• Changelog

• Multi-Path Feature Processing

• Evolution of Group Convolution

• Fancy Convolutions

• Mixing Convolutions

• Attention Structures in Image Domains

• Multi-Scale Feature Extraction

• New Patterns of ASPP

• Considerations of Dilated Convolutions

• Deep Supervision

• SE/SK/M&R

• Novel Structures

• Related Materials

Multi-Path Feature Processing

• Identity mapping (https://www.yuque.com/lart/architecture/db7i2a#sNMiq)

• (arxiv 2016) RESNET IN RESNET: GENERALIZING RESIDUAL ARCHITECTURES (https://www.yuque.com/lart/architecture/db7i2a#BBwPC)
• (ICLR 2018) LOG-DENSENET: HOW TO SPARSIFY A DENSENET (https://www.yuque.com/lart/architecture/db7i2a#2r6Xt)
• (ECCV 2018) Sparsely Aggregated Convolutional Networks (https://www.yuque.com/lart/architecture/db7i2a#Z015s)

• Multi-branch (https://www.yuque.com/lart/architecture/db7i2a#MHuqj)

• (ICCV 2019) Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution (https://www.yuque.com/lart/architecture/db7i2a#dNFUy)

• (CVPR 2019) ELASTIC: Improving CNNs with Dynamic Scaling Policies (https://www.yuque.com/lart/architecture/db7i2a#wIMKs)

• (CVPR 2019) Deep High-Resolution Representation Learning for Human Pose Estimation (HRNet) (https://www.yuque.com/lart/architecture/db7i2a#XDV4W)

• (arxiv) High-Resolution Representations for Labeling Pixels and Regions (HRNetV2) (https://www.yuque.com/lart/architecture/db7i2a#RFPoS)

• (CVPR 2017) Multigrid Neural Architectures (https://www.yuque.com/lart/architecture/db7i2a#2jve3)

• (arxiv 2016) Deeply-Fused Nets (https://www.yuque.com/lart/architecture/db7i2a#BVMXu)

• (IJCAI 2018) Deep Convolutional Neural Networks with Merge-and-Run Mappings (https://www.yuque.com/lart/architecture/db7i2a#pfrES)

Evolution of Group Convolution

• AlexNet (2012) (https://www.yuque.com/lart/architecture/group#7mobe)

• (CVPR 2017) ResNeXt (https://www.yuque.com/lart/architecture/group#7phku)

• (MMM 2017) Logarithmic Group Convolution (https://www.yuque.com/lart/architecture/group#cGiXD)

• (CVPR 2017) Deep Roots (https://www.yuque.com/lart/architecture/group#eIk8T)

• (arixv 2014) Rigid-Motion Scattering for Texture Classification (https://www.yuque.com/lart/architecture/group#ALoI3)

• (ICCV 2017) Factorized Convolutional Neural Networks (https://www.yuque.com/lart/architecture/group#NaHZ4)

• (arixv 2016) Xception (https://www.yuque.com/lart/architecture/group#4o328)

• (arxiv 2017) MobileNet (https://www.yuque.com/lart/architecture/group#k0YUN)

• (ICCV 2019) HBONet: Harmonious Bottleneck on Two Orthogonal Dimensions (https://www.yuque.com/lart/architecture/group#74Z7o)

• (ICCV 2017) IGCV1: Interleaved Group Convolutions for Deep Neural Networks (https://www.yuque.com/lart/architecture/group#rxMY2)

• (CVPR 2018) IGCV2: Interleaved Structured Sparse Convolutional Neural Networks (https://www.yuque.com/lart/architecture/group#CnFUw)

• (BMVC 2018) IGCV3: Interleaved Low-Rank Group Convolutions for Efficient Deep Neural Networks (https://www.yuque.com/lart/architecture/group#GMxWY)

• (CVPR 2018) ShuffleNetV1 (https://www.yuque.com/lart/architecture/group#Kh3DL)

• Other Related Articles (https://www.yuque.com/lart/architecture/group#XCSB0)

Fancy Convolutions

• (ICLR 2015) Flatted Convolution (https://www.yuque.com/lart/architecture/conv#uGzbq)

• (ICCV 2019) 4-Connected Shift Residual Networks (https://www.yuque.com/lart/architecture/conv#VIBd6)

Mixing Convolutions

• MixNet: Mixed Depthwise Convolutional Kernels (https://www.yuque.com/lart/architecture/mixnet#4d9jS)

• Res2Net: A New Multi-scale Backbone Architecture (https://www.yuque.com/lart/architecture/mixnet#w6WTr)

Attention Structures in Image Domains

• Residual Attention Network for Image Classification (https://www.yuque.com/lart/architecture/vw6t5t#cNg2C)

• Attention Augmented Convolutional Networks (https://www.yuque.com/lart/architecture/vw6t5t#xcDTJ)

• Graph-Based Global Reasoning Networks (https://www.yuque.com/lart/architecture/vw6t5t#TeeOb)

• SRM : A Style-based Recalibration Module for Convolutional Neural Networks (https://www.yuque.com/lart/architecture/vw6t5t#fHk1g)

• Spatial Group-wise Enhance: Improving Semantic Feature Learning in Convolutional Networks (https://www.yuque.com/lart/architecture/vw6t5t#5yiAM)

• Non-local Neural Networks (https://www.yuque.com/lart/architecture/vw6t5t#1rIG9)

• Asymmetric Non-local Neural Networks for Semantic Segmentation (https://www.yuque.com/lart/architecture/vw6t5t#HHV2p)

• Compact Generalized Non-local Network (https://www.yuque.com/lart/architecture/vw6t5t#eIgbE)

• A2-Nets: Double Attention Networks (https://www.yuque.com/lart/architecture/vw6t5t#f1LV0)

• GCNet: Non-local Networks Meet Squeeze-Excitation Networks and Beyond (https://www.yuque.com/lart/architecture/vw6t5t#iHP1x)

• CBAM: Convolutional Block Attention Module (https://www.yuque.com/lart/architecture/vw6t5t#VL9QW)

• BAM: Bottleneck Attention Module (https://www.yuque.com/lart/architecture/vw6t5t#tH1FF)

• A Relation-Augmented Fully Convolutional Network for Semantic Segmentationin Aerial Scenes (https://www.yuque.com/lart/architecture/vw6t5t#8aEEw)

• Dual Attention Network for Scene Segmentation (https://www.yuque.com/lart/architecture/vw6t5t#1e4w5)

• Related Links (https://www.yuque.com/lart/architecture/vw6t5t#0pYLl)

• References (https://www.yuque.com/lart/architecture/vw6t5t#EuuVn)

• Review Papers (https://www.yuque.com/lart/architecture/vw6t5t#LZ7gr)

Multi-Scale Feature Extraction

• PPM (https://www.yuque.com/lart/architecture/mutli#A095s)

• ASPP (https://www.yuque.com/lart/architecture/mutli#x7GOY)

• GPM (https://www.yuque.com/lart/architecture/mutli#xrRq4)

• FPA (https://www.yuque.com/lart/architecture/mutli#REGYY)

• Omni-Scale Residual Block (https://www.yuque.com/lart/architecture/mutli#E2GkI)

New Patterns of ASPP

• DenseASPP (https://www.yuque.com/lart/architecture/moreaspp#A2Lp6)

Considerations of Dilated Convolutions

• HDC (https://www.yuque.com/lart/architecture/moredilated#4lXNe)

• Dilated Residual NetWorks (https://www.yuque.com/lart/architecture/moredilated#J0CcE)

• Smoothed Dilated Convolutions (https://www.yuque.com/lart/architecture/moredilated#BgmZO)

Deep Supervision

• DSN (https://www.yuque.com/lart/architecture/dsn)

SE/SK/M&R

• SE (https://www.yuque.com/lart/architecture/upvx1p#bMTs0)

• SK (https://www.yuque.com/lart/architecture/upvx1p#bzKZs)

• M&R (https://www.yuque.com/lart/architecture/upvx1p#KJWYv)

Novel Structures

• FRACTALNET: ULTRA-DEEP NEURAL NETWORKS WITHOUT RESIDUALS (https://www.yuque.com/lart/architecture/arch#uplDt)

• Deep Pyramidal Residual Networks (https://www.yuque.com/lart/architecture/arch#I57ao)

• Deep Layer Aggregation (https://www.yuque.com/lart/architecture/arch#iuakf)

• UNet++: A Nested U-Net Architecture for Medical Image Segmentation (https://www.yuque.com/lart/architecture/arch#492Mv)

Related Materials

• DEEP CONVOLUTIONAL NEURAL NETWORK DESIGN PATTERNS：[https://arxiv.org/pdf/1611.00847.pdf (https://arxiv.org/pdf/1611.00847.pdf)

Recommended Reading:
The Differences and Connections Between Fully Connected Graph Convolution Networks (GCN) and Self-Attention Mechanisms
Complete Guide to Graph Convolution Networks (GCN) for Beginners

Paper Appreciation [ACL18] Component-based Syntactic Analysis Based on Self-Attentive