
An artificial neural network is actually like a complex calculator; you input something, and it gives you a result. Just like when you input 2+2 into a calculator, it outputs 4, but an artificial neural network can handle more than just basic arithmetic; it can process more complex things like images, text, etc. So when we say that an artificial neural network is a function approximator, we mean it can simulate various complex computation processes, helping us achieve the desired output from the input.

If it’s a picture of a car, there must be a function that can take this image and predict what type of car it is, just from those raw pixel values.

For traditional programming, if there is a piece of English text, there must be a function that can take this text and output the same text but in Chinese.

If you have a question, there must be a function that can generate an answer.
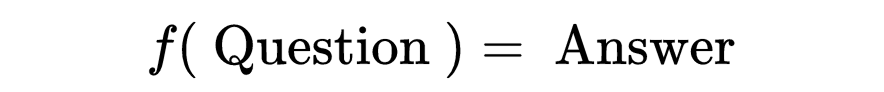
But the problem is, in traditional programming, we have always been writing functions that are very powerful, but what happens when the function is so complex that we cannot explain it? For example, when you see this number,

You know it’s 5, but if you had to write an algorithm that takes this image and says it’s 5, suddenly this becomes extremely difficult.
The task is simple, but writing a function that takes an image of a handwritten digit and outputs which digit it is, is very difficult, which is why we need machine learning. The idea here is simple: if we know there exists a function that can solve this problem, but we do not know what that function looks like, maybe we can define a structure, an artificial neural network, that can learn this function, and to learn this function, it needs something to learn from, which means it needs data, like many different images of handwritten digits.
Let’s look at a very simple example,
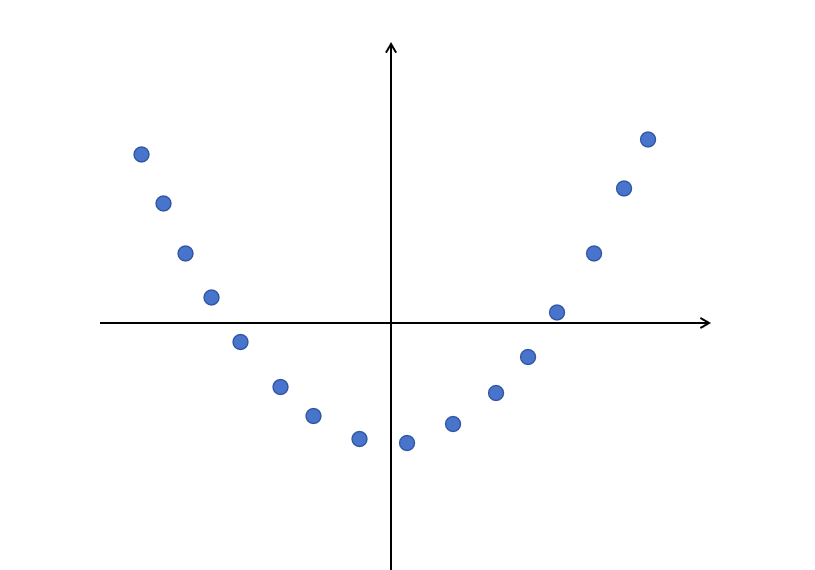
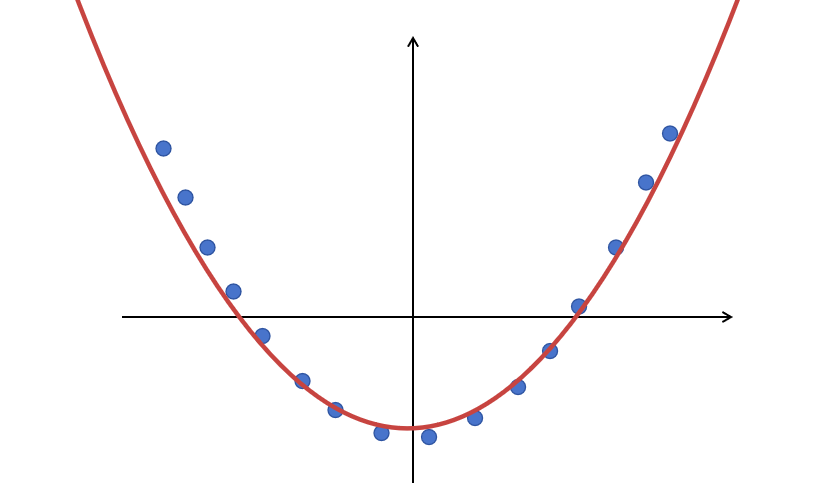
You can see some data points; if I ask you what the function that simulates these data is, you might imagine a curve passing through these data points. This is what the neural network should also learn; it should learn to approximate the function represented by these data. If a new x value appears, we should be able to predict the y value, even if we did not know this point before.
Back to handwritten digits, a very famous dataset of handwritten digits is called MNIST, which contains thousands of handwritten digits.

If you want to create a model that learns from this data to be able to recognize unseen handwritten digits, you can take inspiration from how the human brain learns.
Our brain is made up of many cells called neurons. Neurons have parts that look like antennas called dendrites, which are used to receive signals from other neurons. The body of the neuron decides whether to pass these signals to the next neuron. If it decides to pass them, the neuron sends the signal through a long line called an axon until the signal reaches another place called a synapse. At the synapse, the signal is passed to the next neuron. This is how our brain processes and transmits information.
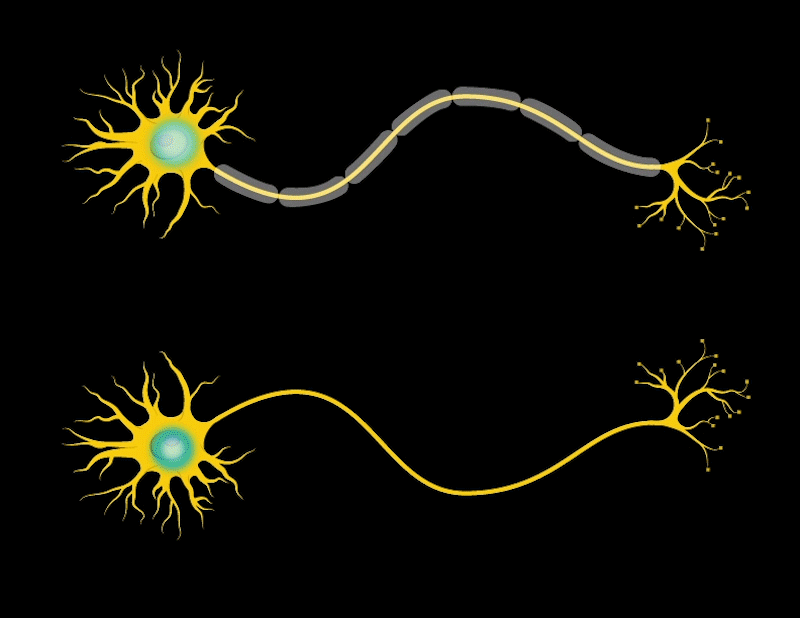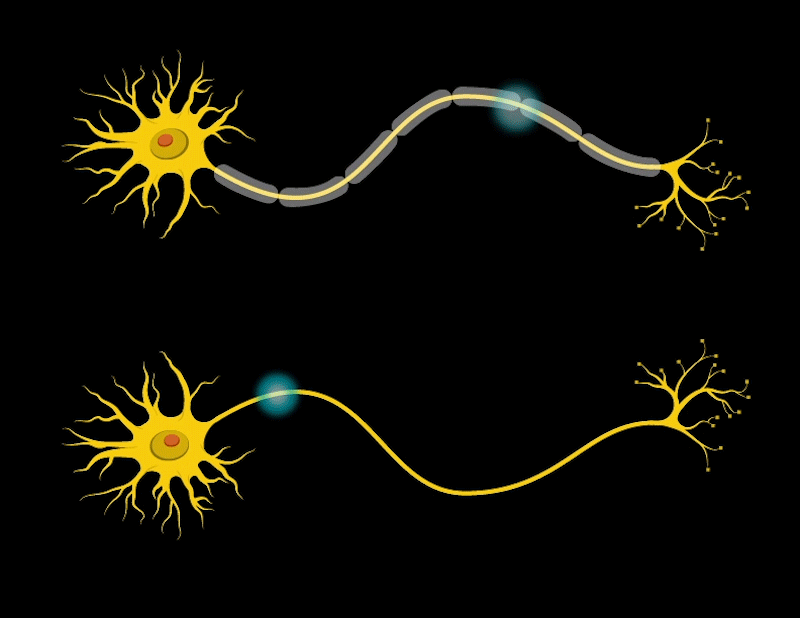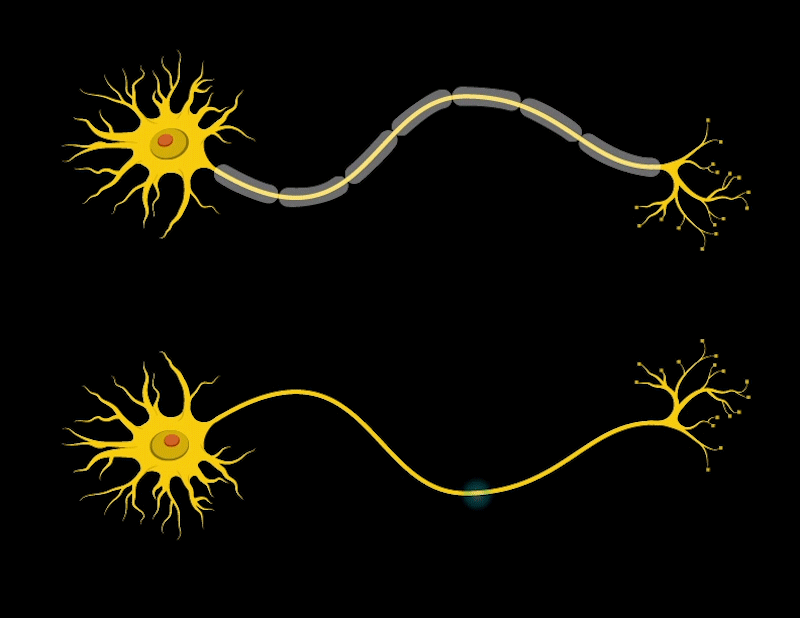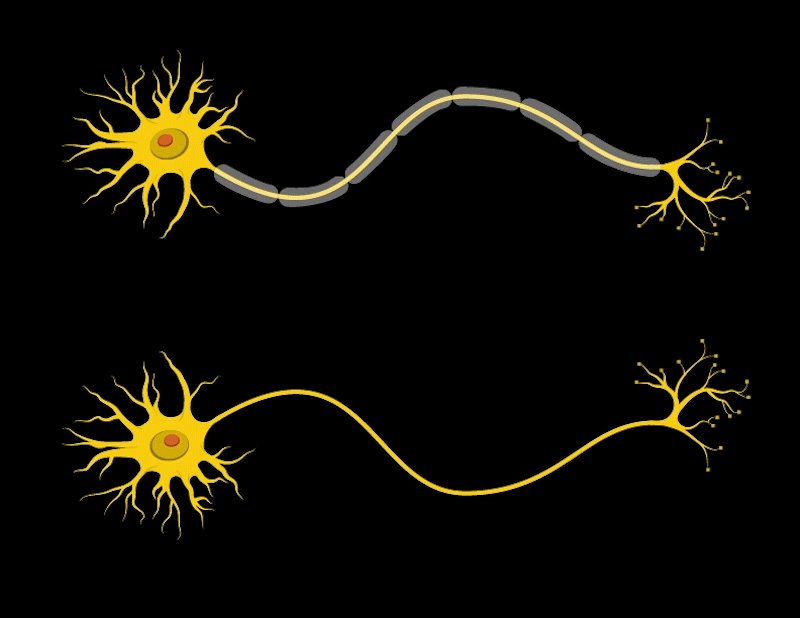
When we learn, the connections between neurons in the brain change; they become stronger, forming new connections, and neurons become more efficient.

Artificial neural networks try to simulate this process; they consist of artificial neurons, which are simple functions that receive values from other neurons and combine them into a signal to be passed to other neurons.

In this specific case, the image above is a 28×28 pixel image, where each pixel value ranges from 0 to 1, with black pixels being 0 and white pixels being 1. These pixels make up the input layer.
Now we want to know which digit the image displays; since there are 10 possible digits, we generate 10 predictions for each input image, so we can add 10 neurons here and call them the output layer.

Each input neuron (a pixel point) will connect to each output neuron (the 10 digits from 0-9), and we connect them with what is called weights, where each weight is just a number that can be randomly chosen at the beginning.
In this example, there are 784 input neurons (corresponding to the 28×28 pixel image), and each input neuron connects to 10 output neurons (corresponding to the 10 possible digits). So there will be a total of 784 pixel points multiplied by 10 digits, which equals 7840 connections. Each connection has a weight, and these weights will be adjusted during training so that the network can correctly recognize the digit in the input image.
Each output neuron will take the input values, multiply each value by the corresponding weight, and sum them to get a new value,
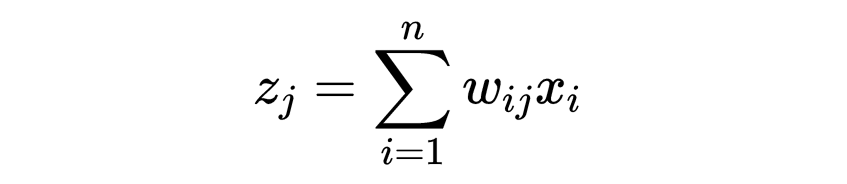
In this example, we expect the neuron representing the digit 5 to give a very high value (weight), while the neurons representing other digits give lower values. This way, the network can correctly identify that the input image is the digit 5.
If the input is the digit 0, once again, only the output neuron representing 0 should light up (receive a high value), this might be the simplest neural network we can build.
But our task is to teach this artificial neural network to recognize these digits, which means we must change the weights in some way to make better predictions. This is done by showing the network a series of sample images (like images of handwritten digits) and then observing whether the network’s predictions are accurate. If the network’s predictions are inaccurate, the weights need to be adjusted.
To know how to adjust the weights, we use a tool called loss function, which helps us measure the difference between the network’s predictions and the actual results. Our goal is to minimize this loss as much as possible, which means our predictions are more accurate.

In fact, if you visualize the weights of each neuron, as the model learns, we can see that although they initially appear random, as the model learns and trains, these weights gradually adjust and start forming specific patterns. These patterns enable the model to recognize the features of different digits, allowing it to distinguish them. Initially, the model may only learn simple linear relationships, meaning it can distinguish some very basic digit features.
To enable the model to learn more complex relationships, we can add more layers between the input layer and the output layer; these additional layers are called hidden layers.

Adding more hidden layers can make the neural network “deeper“, which is the concept of “deep learning”. The neurons in the hidden layers work similarly to those in the output layer, but each neuron also has an activation function, which can be non-linear, allowing the model to learn more complex relationships and thus improve the accuracy of digit recognition.
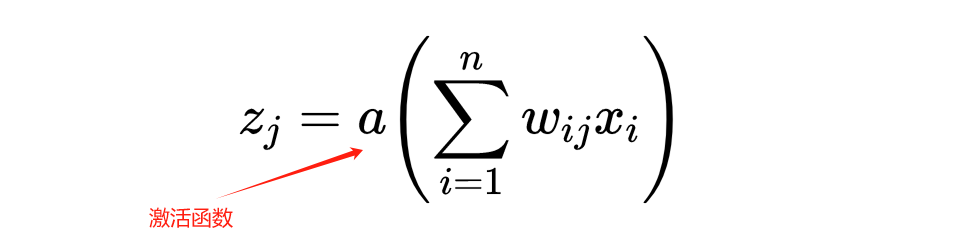
Back to the simple two-dimensional function example, the activation function will allow us to bend the straight line so that we can more accurately simulate the data.
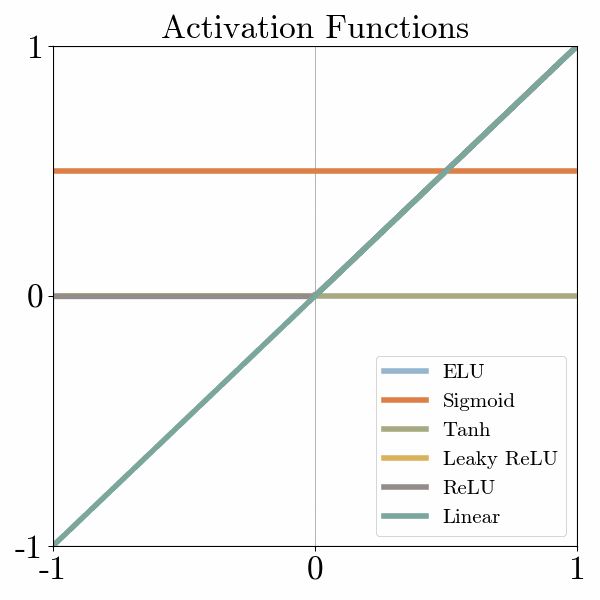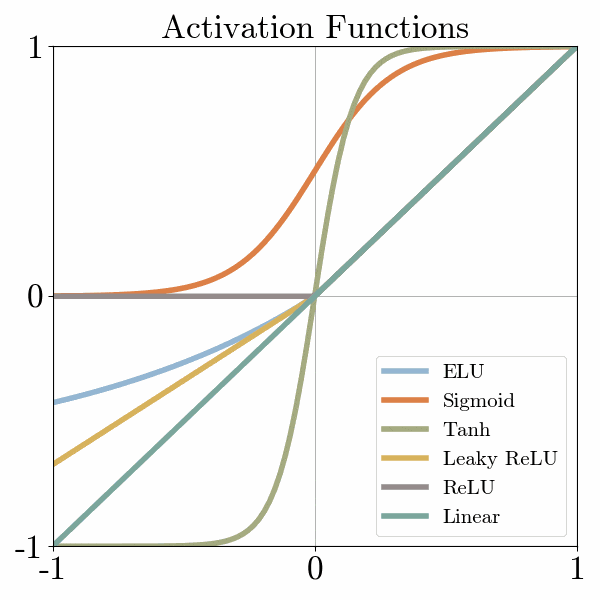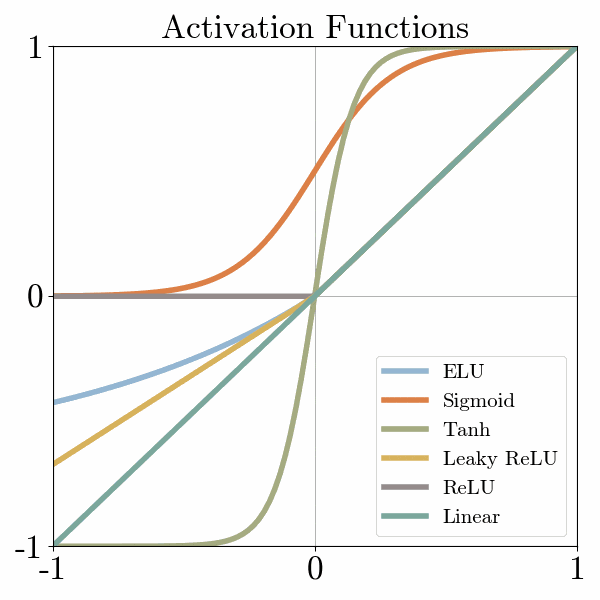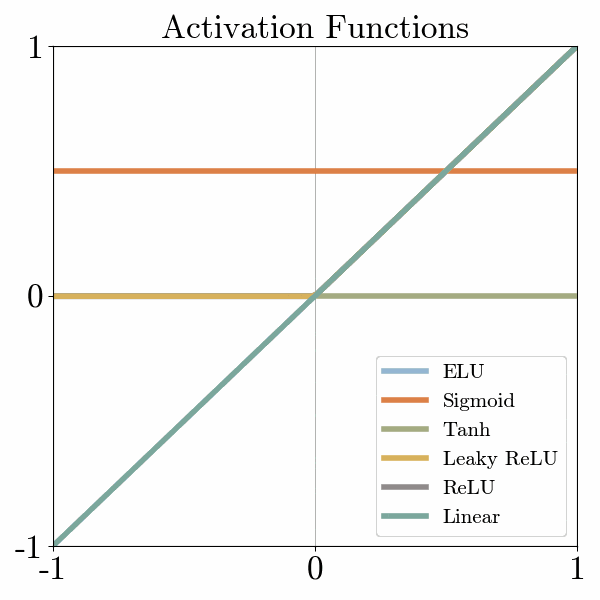
There are many activation functions, but one of the simplest is called ReLu, which turns negative numbers to 0 and keeps positive numbers unchanged.
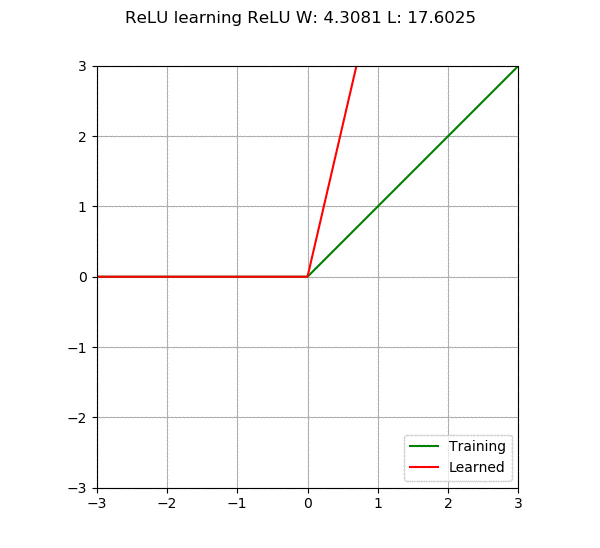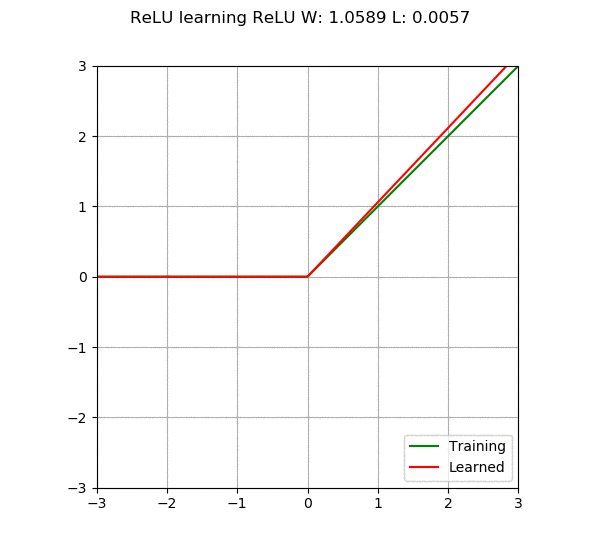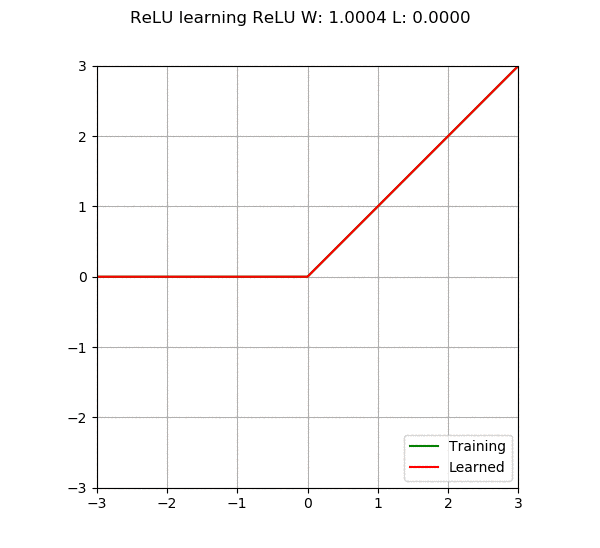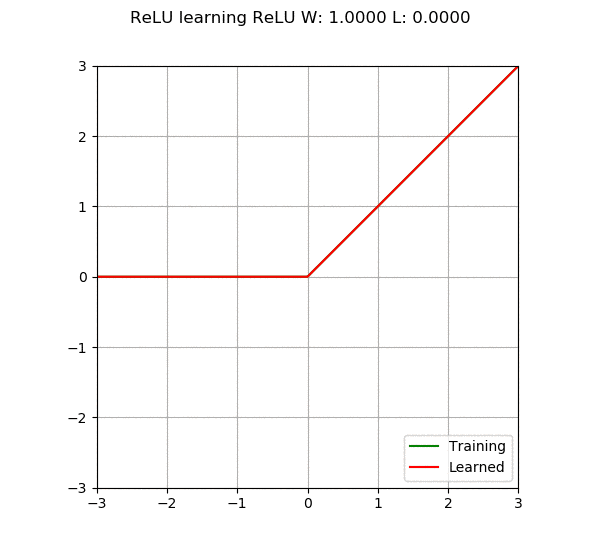
When we add more neurons or layers to the neural network, its capability increases, meaning it can learn more complex things. However, there is a problem: if we make the network too large, it may become too “smart” to the point that it not only learns what we want it to learn but also memorizes all the training data. This situation is called overfitting, just like the model becomes too focused on the training data that it performs poorly when faced with new, unseen data. On the other hand, if the model is too simple, it may not learn enough, which is called underfitting. Therefore, the main goal of neural networks is to find a balance point, building a model that is neither too complex nor too simple, capable of learning patterns from the data.
