


Click the blue text above to follow us


In recent years, the attention mechanism has become very popular due to its effectiveness, and the combination of attention with various networks is increasingly common.
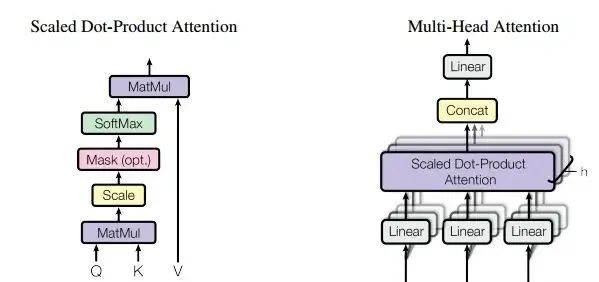
MATLAB 2023 has added the Attention layer, making the implementation of the attention mechanism extremely simple. The detailed usage can be found by directly using the following help command in the command line.
>> help selfAttentionLayer
Below is a brief introduction to the usage of the attention mechanism.
layer = selfAttentionLayer(8,256)This represents the creation of a self-attention layer with 8 heads, 256 keys, and query channels, and 2 value channels.
Next, we will introduce some practical regression examples of attention networks. Note that only versions above 2023 can use this feature. 【Data code acquisition method is at the end of the article】

MATLAB Deep Learning Loss Training Curve
Previously, many friends asked me how to plot the loss line. If you find MATLAB’s built-in training graph unsatisfactory for inclusion in papers, I accidentally discovered that it is actually quite simple.
[Mdl,Loss] = trainNetwork(x_train_regular, y_train_regular, layers, options);%%figuresubplot(2, 1, 1)plot(1 : length(Loss.TrainingRMSE), Loss.TrainingRMSE, 'r-', 'LineWidth', 1)xlabel('Iteration Count')ylabel('Root Mean Square Error')legend('Training Set Root Mean Square Error')title ('Training Set Root Mean Square Error Curve')gridset(gcf,'color','w')
subplot(2, 1, 2)plot(1 : length(Loss.TrainingLoss), Loss.TrainingLoss, 'b-', 'LineWidth', 1)xlabel('Iteration Count')ylabel('Loss Function')legend('Training Set Loss Value')title ('Training Set Loss Function Curve')gridset(gcf,'color','w')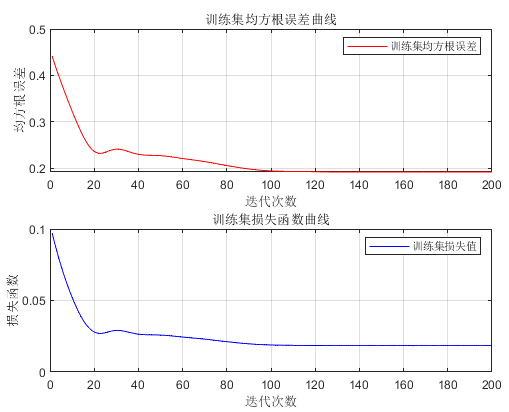
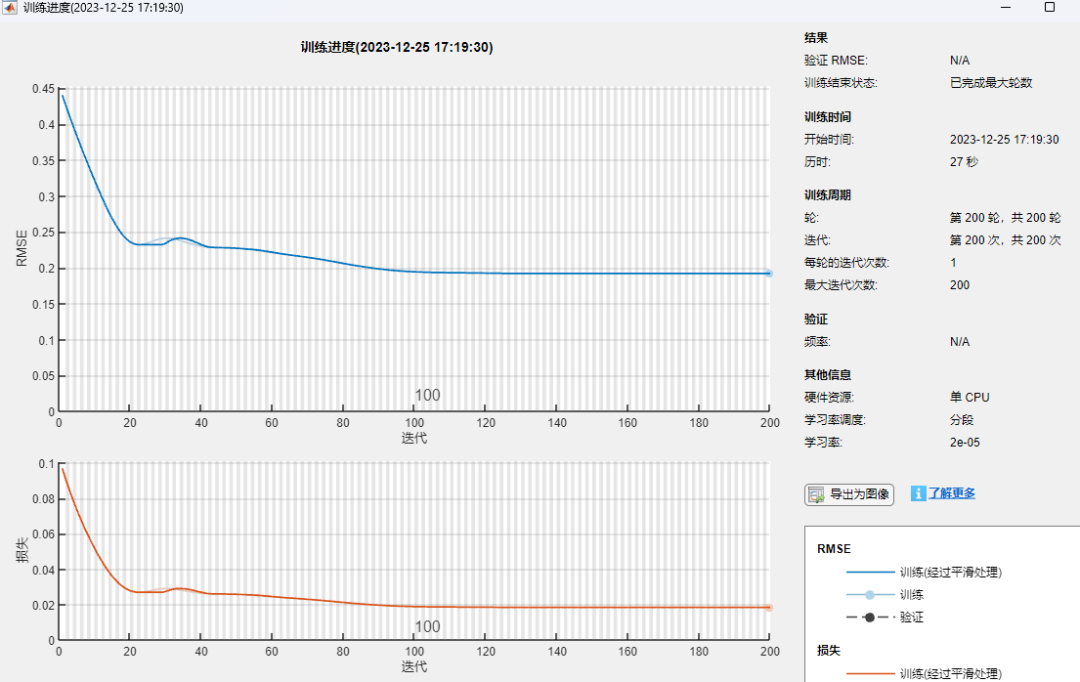

MATLAB Training Hyperparameter Settings
The hyperparameter settings for MATLAB deep learning are implemented in the options. The detailed meanings can be found by using help trainingOptions, which include the choice of optimizer, epoch, and batch size, all common hyperparameters that can be adjusted.
options = trainingOptions('adam', ... 'MaxEpochs',200,... 'MiniBatchSize',min_batchsize,... 'InitialLearnRate',0.001,... 'LearnRateSchedule','piecewise', ... 'LearnRateDropPeriod',125, ... 'LearnRateDropFactor',0.02, ... 'Plots','training-progress');The choice of optimizer mainly includes the following four options. Starting from version R2023b, the LBFGS optimizer is supported. L-BFGS is a batch solver. The L-BFGS algorithm is best suited for small networks and datasets that can be processed in a single batch. Finally, we will introduce the usage of L-BFGS, which has some differences from ordinary networks.
-
<span>"sgdm"</span>— Stochastic gradient descent with momentum (SGDM). SGDM is a stochastic solver. -
<span>"rmsprop"</span>— Root mean square propagation (RMSProp). RMSProp is a stochastic solver. -
<span>"adam"</span>— Adaptive moment estimation (Adam). Adam is a stochastic solver. -
<span>"lbfgs"</span>(since R2023b) — Limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS). L-BFGS is a batch solver. The L-BFGS algorithm is best suited for small networks and data sets that you can process in a single batch.

1. NN-attention
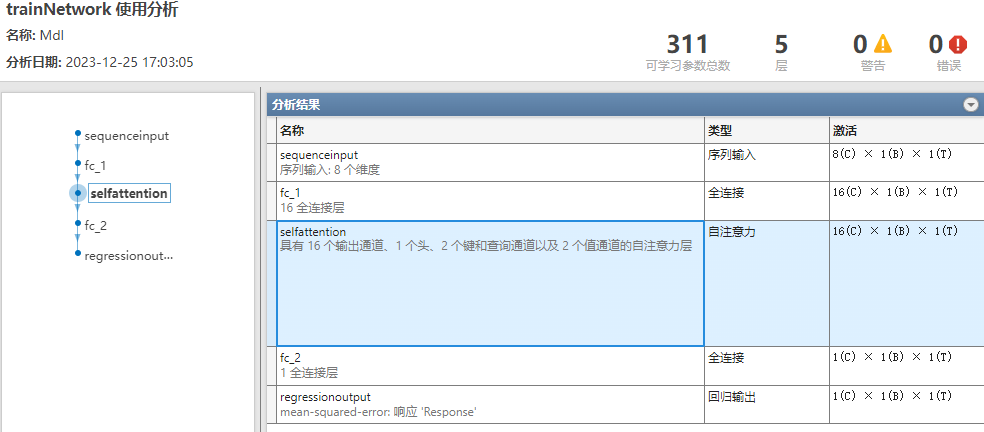
Using the classic abalone dataset with 8 inputs and 1 output, we construct a fully connected layer with 16 hidden layers, and then construct a single-head attention mechanism.
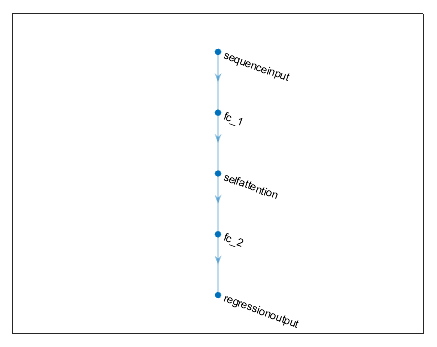
The complete code is as follows:
clc;clear;close all;load('abalone_data.mat')%%[m,n]=size(data);train_num=round(0.8*m); %Independent variable x_train_data=data(1:train_num,1:n-1);y_train_data=data(1:train_num,n);x_test_data=data(train_num+1:end,1:n-1);y_test_data=data(train_num+1:end,n);x_train_data=x_train_data';y_train_data=y_train_data';x_test_data=x_test_data';[x_train_regular,x_train_maxmin] = mapminmax(x_train_data);[y_train_regular,y_train_maxmin] = mapminmax(y_train_data);%Create network%%Call format%%min_batchsize=100;layers = [ sequenceInputLayer(size(x_train_data,1)) fullyConnectedLayer(16) selfAttentionLayer(1,2) fullyConnectedLayer(size(y_train_data,1)) regressionLayer];options = trainingOptions('adam', ... 'MaxEpochs',200,... 'MiniBatchSize',min_batchsize,... 'InitialLearnRate',0.001,... 'LearnRateSchedule','piecewise', ... 'LearnRateDropPeriod',125, ... 'LearnRateDropFactor',0.02, ... 'Plots','training-progress');[Mdl,Loss] = trainNetwork(x_train_regular, y_train_regular, layers, options);%%figuresubplot(2, 1, 1)plot(1 : length(Loss.TrainingRMSE), Loss.TrainingRMSE, 'r-', 'LineWidth', 1)xlabel('Iteration Count')ylabel('Root Mean Square Error')legend('Training Set Root Mean Square Error')title ('Training Set Root Mean Square Error Curve')gridset(gcf,'color','w')
subplot(2, 1, 2)plot(1 : length(Loss.TrainingLoss), Loss.TrainingLoss, 'b-', 'LineWidth', 1)xlabel('Iteration Count')ylabel('Loss Function')legend('Training Set Loss Value')title ('Training Set Loss Function Curve')gridset(gcf,'color','w')%% 需要分析网络graph = layerGraph(Mdl.Layers); figure; plot(graph) analyzeNetwork(Mdl) %%x_test_regular = mapminmax('apply',x_test_data,x_train_maxmin);y_test_regular=predict(Mdl,x_test_regular,"MiniBatchSize",min_batchsize);attention_predict=mapminmax('reverse',y_test_regular,y_train_maxmin);%%attention_predict=attention_predict';errors_nn=sum(abs(attention_predict-y_test_data)./(y_test_data))/length(y_test_data);figurecolor=[111,168,86;128,199,252;112,138,248;184,84,246]/255;plot(y_test_data,'Color',color(2,:),'LineWidth',1)hold onplot(attention_predict,'*','Color',color(1,:))hold ontitlestr=['attention neural network',' Error: ',num2str(errors_nn)];title(titlestr)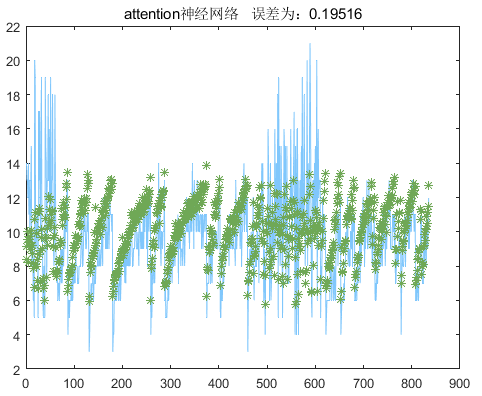
The effect is actually average, possibly because the task is too simple, and it does not fully demonstrate its potential. In fact, a simple one-layer BP network performs quite well too.

2 LSTM-attention
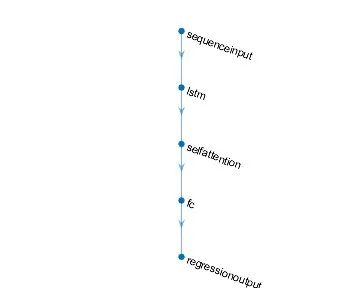
Using the classic abalone dataset with 8 inputs and 1 output, we construct a LSTM layer with 16 hidden layers, and then construct a single-head attention mechanism.
The complete source code is as follows:
clc;clear;close all;load('abalone_data.mat')%%[m,n]=size(data);train_num=round(0.8*m); %Independent variable x_train_data=data(1:train_num,1:n-1);y_train_data=data(1:train_num,n);x_test_data=data(train_num+1:end,1:n-1);y_test_data=data(train_num+1:end,n);x_train_data=x_train_data';y_train_data=y_train_data';x_test_data=x_test_data';[x_train_regular,x_train_maxmin] = mapminmax(x_train_data);[y_train_regular,y_train_maxmin] = mapminmax(y_train_data);x_test_regular = mapminmax('apply',x_test_data,x_train_maxmin);y_train_regular1=y_train_regular';%Create network%%Call formatfor i = 1: size(x_train_regular,2) %Modify input to cell format p_train1{i, 1} = (x_train_regular(:,i)); end for i = 1 : size(x_test_regular,2) p_test1{i, 1} = (x_test_regular(:,i)); end %%min_batchsize=100;layers = [ sequenceInputLayer(size(x_train_data,1)) lstmLayer(16,'OutputMode','last') selfAttentionLayer(1,2) fullyConnectedLayer(1) regressionLayer]; options = trainingOptions('adam', ... 'MaxEpochs',200,... 'MiniBatchSize',min_batchsize,... 'InitialLearnRate',0.001,... 'LearnRateSchedule','piecewise', ... 'LearnRateDropPeriod',125, ... 'LearnRateDropFactor',0.02, ... 'Plots','training-progress');[Mdl,Loss] = trainNetwork(p_train1, y_train_regular1, layers, options);%%figuresubplot(2, 1, 1)plot(1 : length(Loss.TrainingRMSE), Loss.TrainingRMSE, 'r-', 'LineWidth', 1)xlabel('Iteration Count')ylabel('Root Mean Square Error')legend('Training Set Root Mean Square Error')title ('Training Set Root Mean Square Error Curve')gridset(gcf,'color','w')
subplot(2, 1, 2)plot(1 : length(Loss.TrainingLoss), Loss.TrainingLoss, 'b-', 'LineWidth', 1)xlabel('Iteration Count')ylabel('Loss Function')legend('Training Set Loss Value')title ('Training Set Loss Function Curve')gridset(gcf,'color','w')%% 需要分析网络graph = layerGraph(Mdl.Layers); figure; plot(graph) analyzeNetwork(Mdl) %%
y_test_regular=predict(Mdl,p_test1,"MiniBatchSize",min_batchsize);attention_predict=mapminmax('reverse',y_test_regular',y_train_maxmin);%%attention_predict=attention_predict';errors_nn=sum(abs(attention_predict-y_test_data)./(y_test_data))/length(y_test_data);figurecolor=[111,168,86;128,199,252;112,138,248;184,84,246]/255;plot(y_test_data,'Color',color(2,:),'LineWidth',1)hold onplot(attention_predict,'*','Color',color(1,:))hold ontitlestr=['lstm-attention neural network',' Error: ',num2str(errors_nn)];title(titlestr)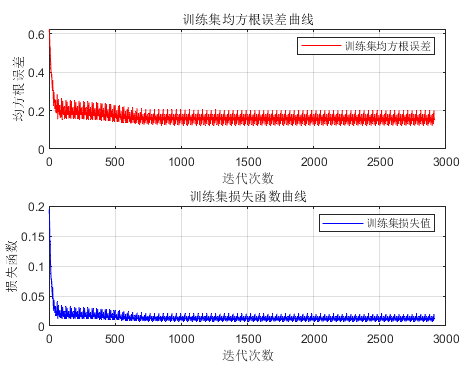
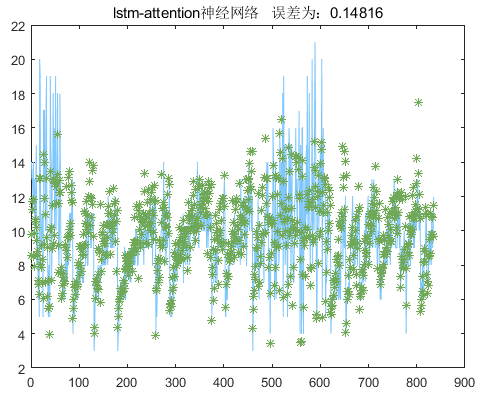
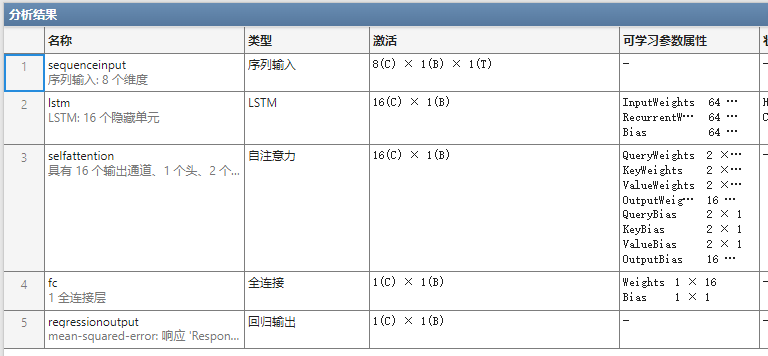

3 NN-attention-LBGFS
The LBFGS optimizer is the latest optimizer introduced in 2023b. I can’t wait to try it out, and its usage is different from common ones. Let’s test it with the abalone data.
clc;clear;close all;load('abalone_data.mat')%%[m,n]=size(data);train_num=round(0.8*m); %Independent variable x_train_data=data(1:train_num,1:n-1);y_train_data=data(1:train_num,n);x_test_data=data(train_num+1:end,1:n-1);y_test_data=data(train_num+1:end,n);x_train_data=x_train_data';y_train_data=y_train_data';x_test_data=x_test_data';[x_train_regular,x_train_maxmin] = mapminmax(x_train_data);[y_train_regular,y_train_maxmin] = mapminmax(y_train_data);%Create network%%Call format%%min_batchsize=100;layers = [ sequenceInputLayer(size(x_train_data,1)) fullyConnectedLayer(16) selfAttentionLayer(1,2) fullyConnectedLayer(size(y_train_data,1)) ];options = trainingOptions('lbfgs',... 'Plots','training-progress');[Mdl,Loss] = trainnet(x_train_regular', y_train_regular', layers, "mean-squared-error",options);%% 需要分析网络graph = layerGraph(Mdl.Layers); figure; plot(graph) analyzeNetwork(Mdl) %%x_test_regular = mapminmax('apply',x_test_data,x_train_maxmin);% y_test_regular=predict(Mdl,x_test_regular,"MiniBatchSize",min_batchsize);y_test_regular=predict(Mdl,x_test_regular');attention_predict=mapminmax('reverse',y_test_regular',y_train_maxmin);%%attention_predict=attention_predict';errors_nn=sum(abs(attention_predict-y_test_data)./(y_test_data))/length(y_test_data);figurecolor=[111,168,86;128,199,252;112,138,248;184,84,246]/255;plot(y_test_data,'Color',color(2,:),'LineWidth',1)hold onplot(attention_predict,'*','Color',color(1,:))hold ontitlestr=['attention neural network',' Error: ',num2str(errors_nn)];title(titlestr)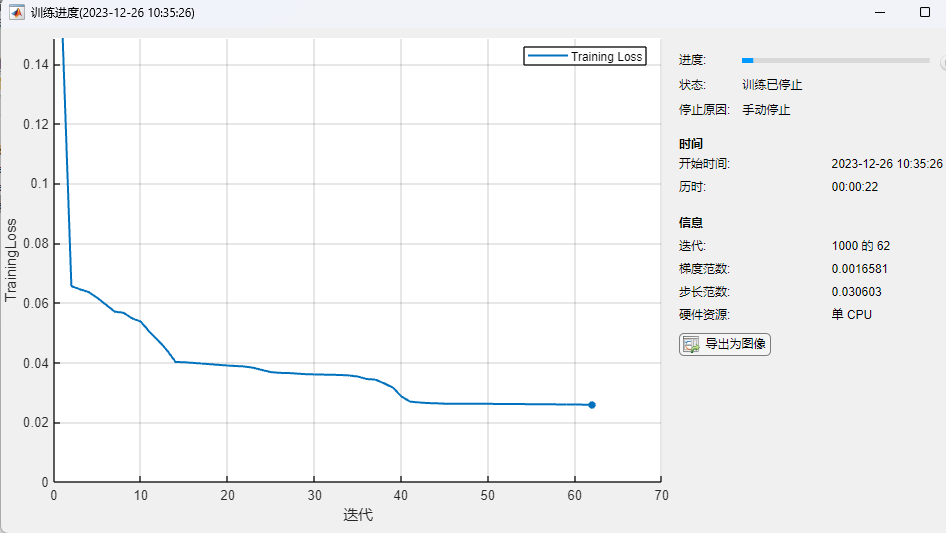
The training progress graph looks like this, and other aspects are similar to other optimizers, with similar results.

4 More Network Layer Introductions
The MATLAB deep learning toolbox is now well-developed, easy to use, and can implement many networks. Detailed network layers can be viewed at the following official link.

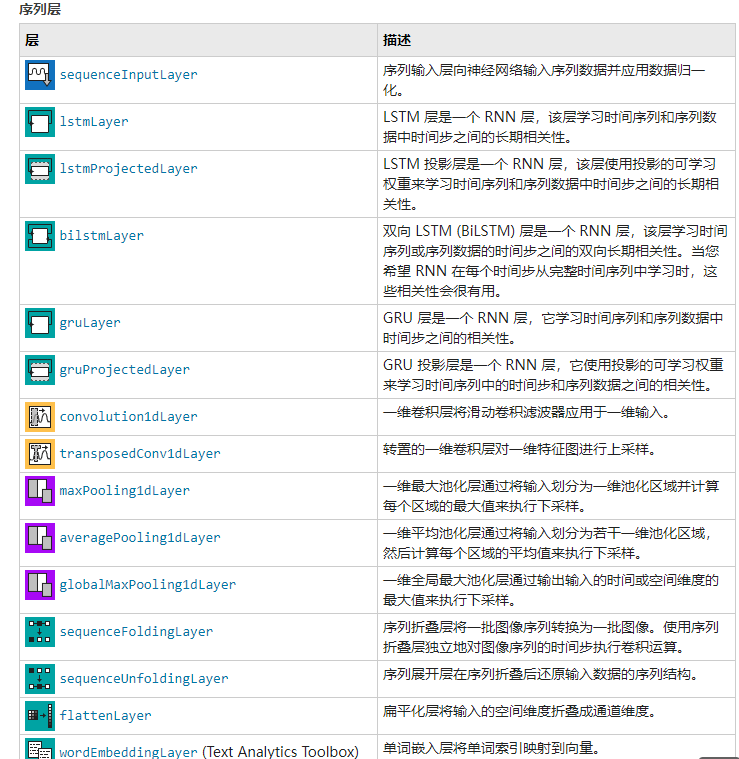
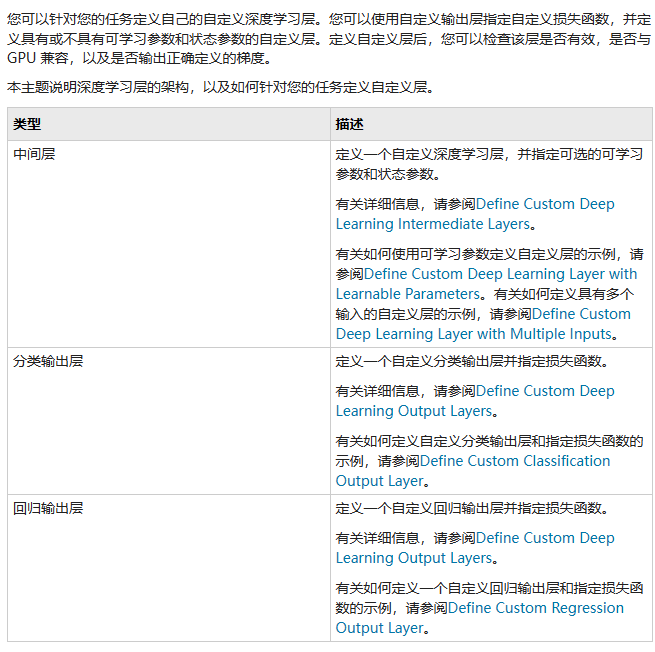

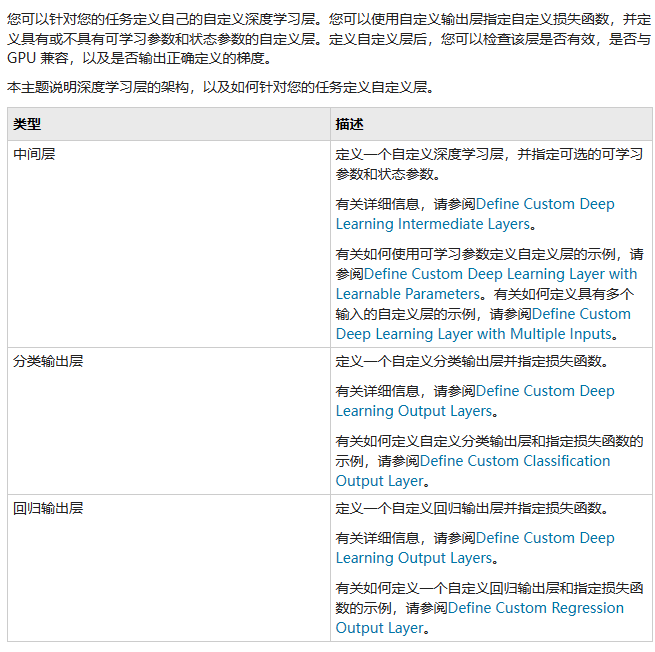
Custom Deep Learning Layers
In addition to direct calls, MATLAB also allows for the implementation of custom deep learning layers. Detailed links are as follows:
Defining Custom Deep Learning Layers – MATLAB & Simulink – MathWorks China

5 Full Series
With just a few keys, you can achieve evaluation, dimensionality reduction, clustering, regression, classification, univariate time series prediction, multivariate time series prediction, and multi-input multi-output problems, with hundreds of commonly used popular algorithms, and support one-click code export, which can be modified and improved later.
Major updates in the magic tool series! | One-click implementation of hundreds of efficient algorithms | Easily solve evaluation, dimensionality reduction, clustering, regression, classification, time series prediction, and multi-input multi-output problems.

Scan to get

The attention mechanism will be added to the toolbox, allowing for the implementation of BiLSTM-attention,CNN-LSTM-attention, TCN-attention, etc. The toolbox is continuously updated.
【Article data source acquisition method】, WeChat public account 【Lvy’s Pocket】 reply to the keyword
【attention】 to get it for free.



MERRY CHIRSTMAS
Click to see your best self.
