1 Overview
In recent years, with the increasing prominence of energy shortages and environmental issues, various forms of clean energy such as solar and wind energy have been widely applied. Microgrids, as an effective means of integrating distributed power sources into the grid, have developed rapidly. The integration of a large amount of new energy and energy storage devices has brought challenges such as complex energy scheduling and low economic efficiency to microgrids. This paper references fuzzy algorithms to predict electricity prices.
Forecasting electricity prices based on the Fuzzy Neural Network (FNN) algorithm is a method that combines fuzzy logic with neural networks, aiming to enhance the accuracy and robustness of the prediction model. In the electricity market, electricity prices are influenced by various factors, including supply and demand relationships, weather conditions, economic activities, and policy adjustments. These factors have complex nonlinear relationships and uncertainties, making electricity price prediction a typical complex problem. The fuzzy neural network provides an effective approach to solve such problems by integrating the capability of fuzzy systems to handle uncertain information with the strong learning ability of neural networks.
Research Background
With the opening of the electricity market and the intensifying competition, accurately predicting electricity prices is crucial for power generation companies to formulate production plans, electricity trading strategies, and assist governments and regulatory agencies in market regulation. Traditional methods such as time series analysis and regression analysis may struggle with the highly nonlinear and uncertain nature of electricity price prediction, while fuzzy neural networks have garnered attention for their unique advantages.
Research Methods
Data Preprocessing: Collect historical electricity price data and relevant factors affecting electricity prices, perform data cleaning, standardization, or normalization to prepare for model input.
Constructing the Fuzzy Neural Network Model: The FNN model typically consists of an input layer, fuzzy layer, rule layer, and output layer. The input layer receives preprocessed data; the fuzzy layer utilizes fuzzy set theory to fuzzify the inputs to handle the uncertainty of the input data; the rule layer establishes the relationship between inputs and outputs based on fuzzy logic; the output layer obtains the final prediction result through a defuzzification process.
Training and Optimization: Model parameters are trained using methods such as backpropagation or genetic algorithms, continually adjusting network weights and thresholds to minimize prediction errors. Multiple iterations may be needed to find the optimal solution.
Model Validation and Testing: The data is divided into training, validation, and testing sets, and techniques such as cross-validation are used to assess the model’s generalization ability and prediction accuracy.
Application Advantages
Handling Uncertainty: Fuzzy logic can effectively manage the uncertain factors influencing electricity prices, such as the unpredictability of weather.
Nonlinear Modeling: Neural networks can learn and express complex nonlinear relationships, improving prediction accuracy.
Adaptive Learning: Fuzzy neural networks possess good adaptability and learning capabilities, allowing the prediction model to adjust over time to adapt to market changes.
Comprehensive Multi-Factor Influence: They can simultaneously consider multiple influencing factors, providing a more comprehensive predictive perspective.
Conclusion
The research on electricity price prediction based on fuzzy neural networks is an interdisciplinary field, combining knowledge from electrical engineering, economics, and computer science. By continuously optimizing model structures and algorithms, improving prediction accuracy and efficiency can provide strong support to participants in the electricity market, helping them make more scientifically sound decisions. However, practical applications must also consider the model’s real-time performance, interpretability, and rapid response capability to emerging factors.
2 Introduction to Fuzzy Neural Networks
Fuzzy neural networks consist of multiple layers including the input layer, fuzzification layer, fuzzy inference layer, normalization layer, and output layer. Their basic structure is shown in Figure 4:

The input sample set of the input layer can be denoted as X, using the fuzzification layer to represent the degree of membership of each input node, and each neural network is represented as a fuzzy criterion with a certain degree of fuzziness, selecting the membership function as a radially symmetric Gaussian function. The output function of the j-th neuron is defined as:

Where cij and σij represent the center and width of the j-th Gaussian membership function, respectively. The output result obtained from the fuzzy inference layer is:
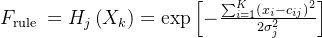
Partial Code:
clc %% Read Data
training = csvread('training_data.csv', 1,1);
testing=csvread('testing_data.csv', 1,1);
%% Remove Outliers:
P = training(:,3);
P1=testing(:,3);
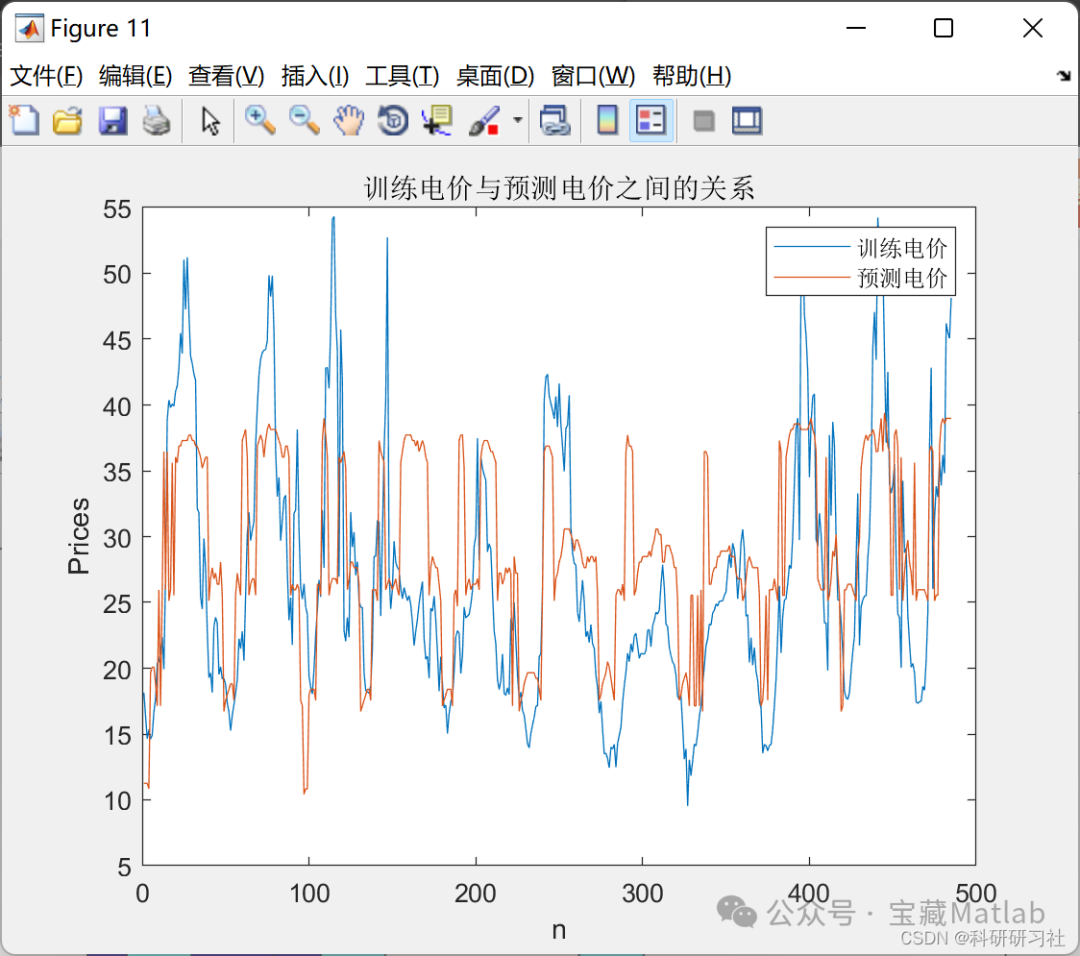
figure('name','Training Data with Outliers');
plot(P,'b*');
Ph=P;
title('Training Data with Outliers')
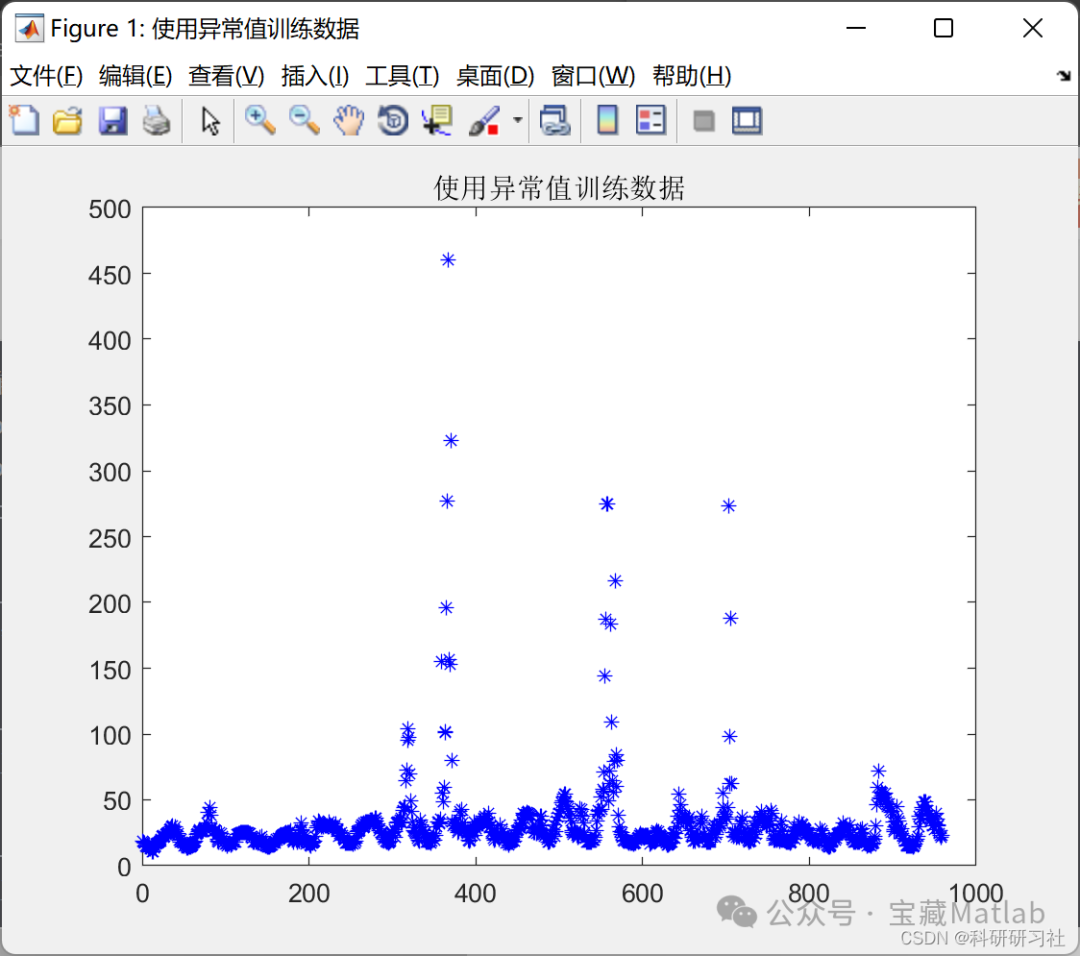
figure('name','Testing Data with Outliers');
plot(P1,'b*');
title('Testing Data with Outliers')
Q1=prctile(P,25);
Q3=prctile(P,75);
range=[Q1-1.5*(Q3-Q1),Q3+1.5*(Q3-Q1)];
position=[find(P>range(2)) find(P<range(1))];
%% Remove Outliers
P(position)=[];
figure
plot(P,'r*');
title('Training Data without Outliers')
figure
subplot(1,2,1)
hist(Ph)
title('Training Data without Outliers')
subplot(1,2,2)
hist(P)
title('Training Data without Outliers')
%% Fuzzy Neural Network
training = removerows(training, position);
T= training(:,1);
D= training(:,2);
P= training(:,3);
t=3:(length(training)-1);
training=[T(t-2), T(t-1),T(t),D(t-2), D(t-1), D(t), P(t+1)];
trainC = corrcoef(training); % Correlation Matrix
%% Define Fuzzy Inputs and Outputs
trainingInputs(:,1) = training(:,6);
trainingInputs(:,2) = training(:,2);
trainingOutputs = training(:,7);
figure
hist(trainingInputs(:,1))
title('Electricity Demand Histogram')
figure
hist(trainingInputs(:,2))
title('Temperature Histogram')
figure
hist(trainingOutputs)
title('Electricity Price Histogram')3 Results








4 References
Some theoretical references are from online literature. If there is any infringement, please contact the author for deletion.
[1] Qi Ji, Li Wei, Ning Liang, Wang Ou, Li Xi. Automation Control System for Power Grid Dispatch Based on Fuzzy Neural Network [J]. Automation of Manufacturing Industry, 2022, 44(01): 118-122.
[2] Zhang Yuhan. Research on Fuzzy Control of Controllable Excitation Linear Motor Based on TS Model [D]. Shenyang University of Technology, 2022. DOI: 10.27322/d.cnki.gsgyu.2022.000323.
5 Matlab Code Implementation
For details, please contact:
