Selected from ArXiv
Authors: Bo-Jian Hou, Zhi-Hua Zhou
Contributors: Si Yuan, Xiao Kun
This article is authorized for reproduction by Almost Human (almosthuman2014)
Reproduction is prohibited
Apart from numerical calculations, do you really know what neural networks are doing internally? We have always understood deep models based on their computational flow, but we are still unclear about whether they have physical or semantic meanings. Especially in Recurrent Neural Networks (RNNs), we only know that at each time step, they utilize previous memories to extract current semantic information, but when it comes to how and what, we are at a loss. In this article, researchers led by Zhou Zhihua from Nanjing University attempt to explore the intrinsic mechanisms of RNNs using finite state machines. This physically meaningful model can reveal the internal processes of RNNs and help us glimpse what RNNs are actually doing.
Structured learning primarily deals with structured outputs, unlike classification problems that predict a value for each independent sample. The structure mentioned here can be graphs, sequences, tree structures, and vectors, etc. Various probabilistic graphical models, perceptrons, and SVMs are commonly used machine learning algorithms for structured outputs. Over the past few decades, structured learning has been widely applied to tasks such as object tracking, object localization, and semantic parsing, while many issues such as multi-label learning and clustering are also closely related to structured learning.
Generally, structured learning uses structured annotations as supervisory information and employs corresponding algorithms to predict these structured information to achieve good performance. However, as machine learning algorithms become increasingly complex, their interpretability becomes more important. Here, interpretability refers to how to understand the intrinsic mechanisms or internal processes of the learning process. In this paper, Zhou Zhihua and other researchers focus on deep learning models and explore how to learn the structures of these models to enhance their interpretability.
Exploring the interpretability of deep learning models is often quite challenging; however, for specific types of deep learning models such as RNNs, we still have methods to address the issue. RNNs, as a major component of deep neural networks, have a very wide range of applications in various sequential data tasks, especially those variants with gating mechanisms, such as gated MGU, GRU with two gates, and LSTM with three gates.
Apart from the familiar RNNs, another tool that can capture sequential data is the finite state machine (FSA). An FSA consists of a finite number of states and transitions between states, which respond to external sequential inputs by transitioning from one state to another. The transition process of an FSA is somewhat similar to that of an RNN, as both receive input elements from the sequence one by one and pass through corresponding states. Unlike RNNs, the internal mechanisms of FSAs are easier to interpret because we can more easily simulate their processes. Furthermore, the transitions between states in an FSA have physical meanings, while RNNs only have numerical computation meanings.
These characteristics of FSAs led Zhou Zhihua’s team to explore learning an FSA model from RNNs and utilize the natural interpretability of FSAs to understand the internal mechanisms of RNNs. Therefore, Zhou Zhihua and his colleagues adopted FSA as the interpretable structure they sought. Additionally, this research differs from previous explorations of structured learning. Previous methods mainly focused on structured predictions or classification results, while this article primarily focuses on the output structure of intermediate hidden layers, so as to better understand the intrinsic mechanisms of RNNs.
To learn an FSA from RNNs and use the FSA to explain the internal mechanisms of RNNs, we need to know how to learn FSA and what specifically to interpret in RNNs. Regarding how to learn FSA, researchers found that the hidden states of non-gated classical RNNs tend to construct clusters. However, there are still some important unresolved issues, one of which is whether the tendency to construct clusters also exists in gated RNNs. We also need to consider efficiency issues, as gated RNN variants are often used on large datasets. As for what specifically to interpret in RNNs, researchers analyzed the role of gating mechanisms in models such as LSTM, GRU, and MGU, particularly the number of gates in different gated RNNs and their impacts. Given that the transitions between states in FSAs have physical meanings, we can infer semantic meanings from the transitions of the corresponding FSA to RNNs.
In this paper, Zhou Zhihua and other researchers attempt to learn an FSA from RNNs. They first verified that the hidden states of other gated RNN variants, apart from non-gated classical RNNs, also have the natural clustering properties. They then proposed two methods: one is an efficient clustering method called k-means++. The other method is based on the phenomenon that hidden states are close in geometric space when they are close in the same sequence, which is named k-means-x. Subsequently, the researchers designed five necessary elements to learn FSA: an alphabet, a set of states, an initial state, a set of accepting states, and state transitions. They finally applied these methods to both simulated and real data.
For the artificially simulated data, the researchers first indicated that we can understand the FSA learned during the running process. They then demonstrated the relationship between accuracy and the number of clusters, indicating that gating mechanisms are essential for gated RNNs, and fewer gates are better. This somewhat explains why the single-gated MGU outperforms other gated RNNs to some extent.
For the sentiment analysis of real data, researchers found that behind the numerical calculations, the hidden states of RNNs do possess the capability to distinguish semantic differences. Because in the corresponding FSA, the words that lead to positive/negative outputs indeed perform some positive or negative human emotional understanding.
Paper: Learning with Interpretable Structure from RNN

Paper link: https://arxiv.org/pdf/1810.10708.pdf
Abstract: In structured learning, the output is often a structure that can be used as supervisory information to achieve good performance. Considering that interpretability in deep learning has received increasing attention in recent years, it would be very helpful if we could learn interpretable structures from deep learning models. In this paper, we focus on Recurrent Neural Networks (RNNs), whose internal mechanisms are still not clearly understood. We find that finite state machines (FSA) that handle sequential data have more interpretable internal mechanisms and can be learned from RNNs as interpretable structures. We propose two different clustering methods to learn FSAs from RNNs. We first present the graphical representation of FSAs to demonstrate their interpretability. From the perspective of FSAs, we analyze how the performance of RNNs is influenced by the number of gates and the semantic meanings behind the numerical hidden state transitions. Our results indicate that RNNs with simpler gating structures, such as the minimum gated unit (MGU), perform better, and transitions in FSAs can yield specific classification results related to corresponding words, a process that is understandable to humans.
Methods Proposed in This Paper
In this section, we introduce the intuitive sources of the proposed methods and the framework of the methods. We represent the hidden states of RNNs as vectors or points. Therefore, when multiple sequences are input into the RNN, a large number of hidden state points accumulate, and they tend to form clusters. To verify this conclusion, we demonstrate the distribution of hidden state points on MGU, SRU, GRU, and LSTM, as shown in Figure 1 (a) to (d).
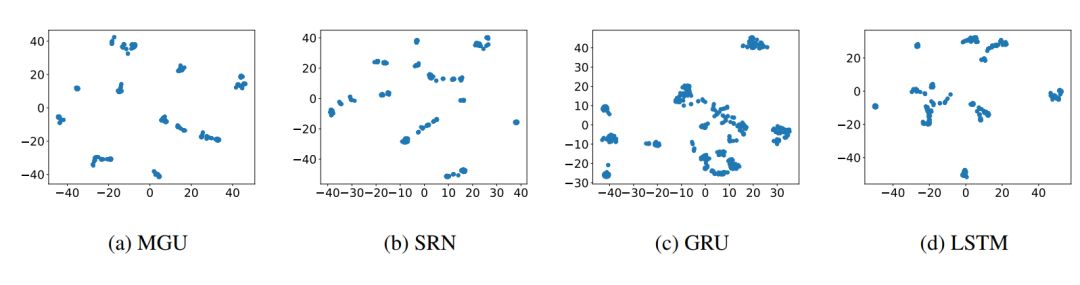
Figure 1: Hidden state points reduced to 2 dimensions using the t-SNE method, showing that hidden state points tend to form clusters.
Figure 2 illustrates the overall framework. We first train the RNN on a training dataset and then perform clustering on all hidden states H corresponding to the validation data V, and finally learn an FSA regarding V. After obtaining the FSA, we can use it to test unlabeled data or directly draw diagrams. In the first step of retraining the RNN, we utilized the same strategy as in [ZWZZ16], omitting the details here. We will then elaborate on the steps of hidden state clustering and FSA learning (see the original text).
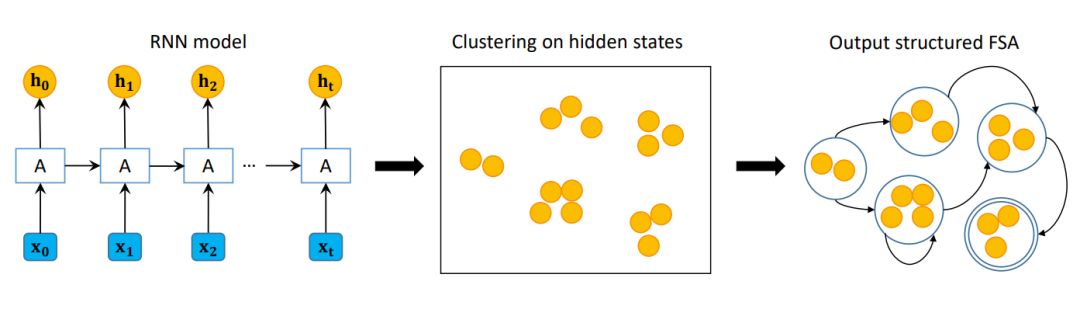
Figure 2: The framework of the proposed algorithm. The yellow circles represent hidden states, denoted as h_t, where t is the time step. “A” is the recurrent unit that receives input x_t and h_t-1 and outputs h_t. The double circle of the structured FSA represents the accepting states. Overall, the framework consists of three steps: training the RNN model, clustering hidden states, and outputting the structured FSA.
The complete process of learning FSA from RNNs is shown in Algorithm 1. We refer to this method as LISOR and demonstrate two different clustering algorithms. The k-means++ based method is called “LISOR-k,” and the k-means-x based method is called “LISOR-x.” By leveraging the clustering tendency of hidden state points, both LISOR-k and LISOR-x can learn well-generalized FSAs from RNNs.

Experimental Results
In this section, we conducted experiments on both artificial and real tasks and visualized the FSAs learned from the corresponding RNN models. Additionally, in both tasks, we discussed how we interpret RNN models from FSAs and demonstrated the accuracy of classification using the learned FSAs.
The first artificial task is to identify the sequence “0110” in a set of sequences of length 4 (containing only 0s and 1s) (Task “0110”). This is a simple task containing only 16 different cases. We included 1000 instances in the training set to improve accuracy by repeating instances. We used all possible values of length 4 0-1 sequences without duplicates to learn the FSA and randomly generated 100 instances for testing.
The second artificial task is to determine whether a sequence contains three consecutive 0s (Task “000”). There is no limit on the length of the sequence, so this task has an infinite instance space and is more challenging than Task “0110”. We randomly generated 3000 training instances of 0-1 with random lengths. We also generated 500 validation instances and 500 test instances.
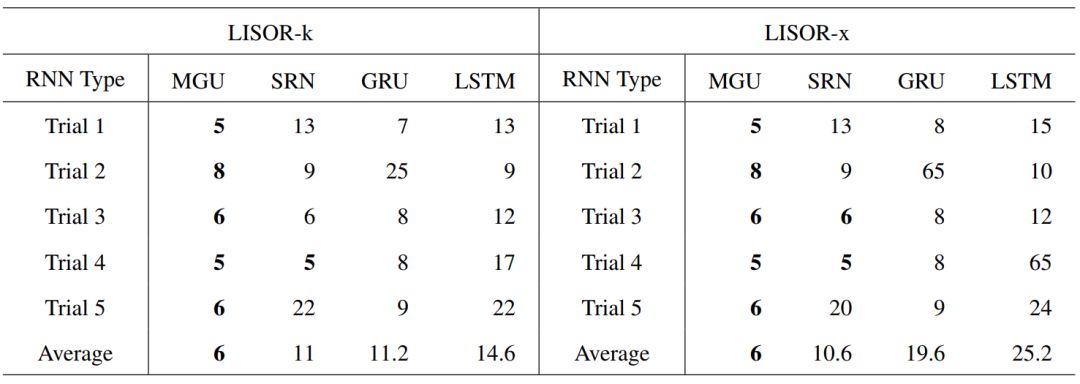
Table 2: The number of clusters (n_c) when the accuracy of the FSA learned from 4 RNNs first reaches 1.0 based on the LISOR-k and LISOR-x methods. Note that these values are more efficient and interpretable when smaller.
As shown in Table 2, we can see that the average number of clusters learned from the FSA of MGU can always reach an accuracy of 1.0 with the minimum number of clusters. A cluster number of 65 means that the accuracy of the FSA cannot reach 1.0 until n_c is 64. The minimum cluster number for each trial and the average minimum cluster number are bolded.
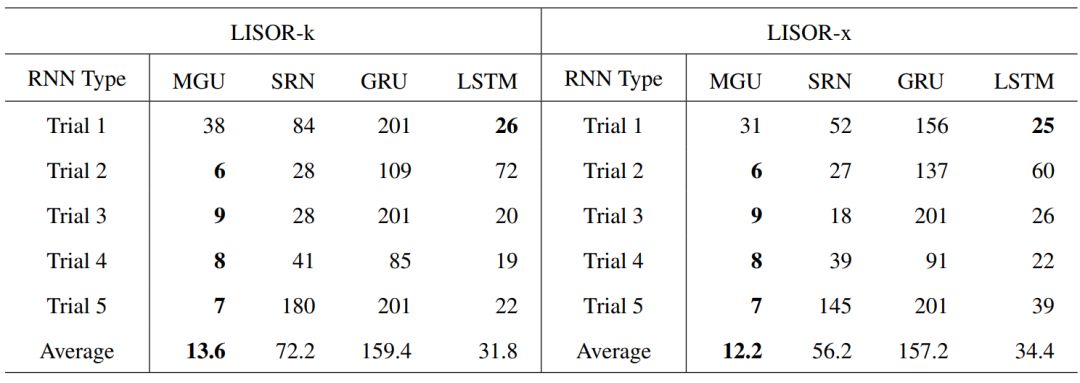
Table 3: The number of clusters (n_c) when the accuracy of the FSA learned from 4 RNNs first reaches 0.7 in Task “000” based on the LISOR-k and LISOR-x methods. Note that these values are more efficient and interpretable when smaller.
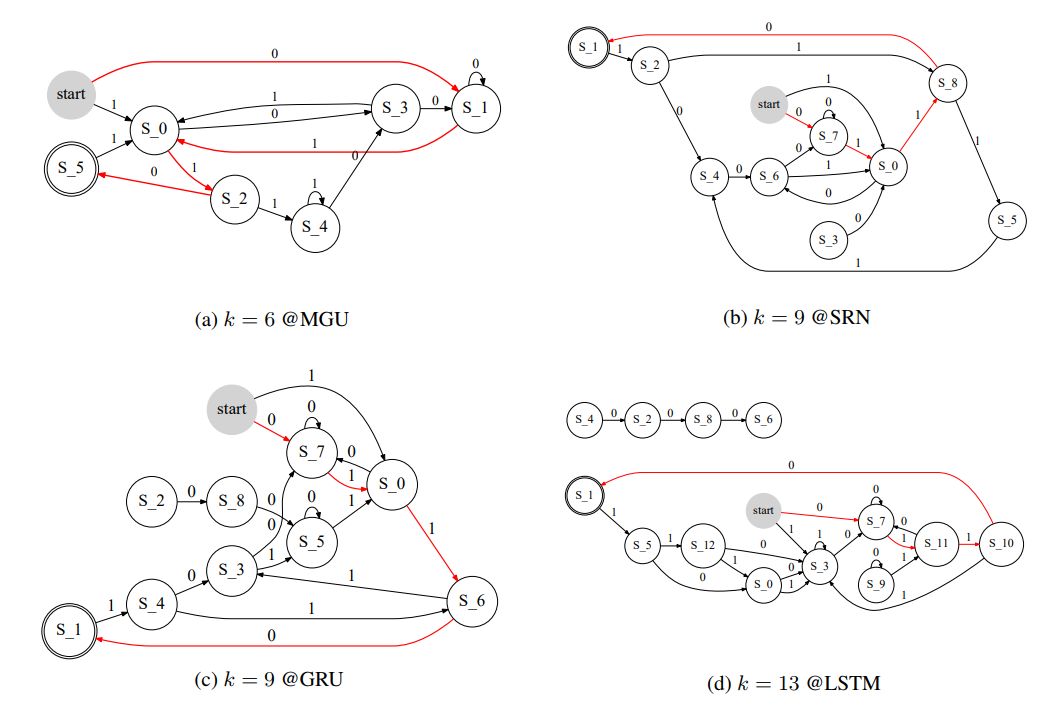
Figure 3: The structure diagram of the FSA learned when training 4 RNNs on Task “0110”. The number of clusters k is determined by the clustering number when the FSA first reaches an accuracy of 1.0. The routing of 0110 is indicated in red. Note that in Figure (d), there are 4 nodes independent of the main parts. This is because we discarded the less frequent transitions when learning a deterministic FSA by inputting a symbol.
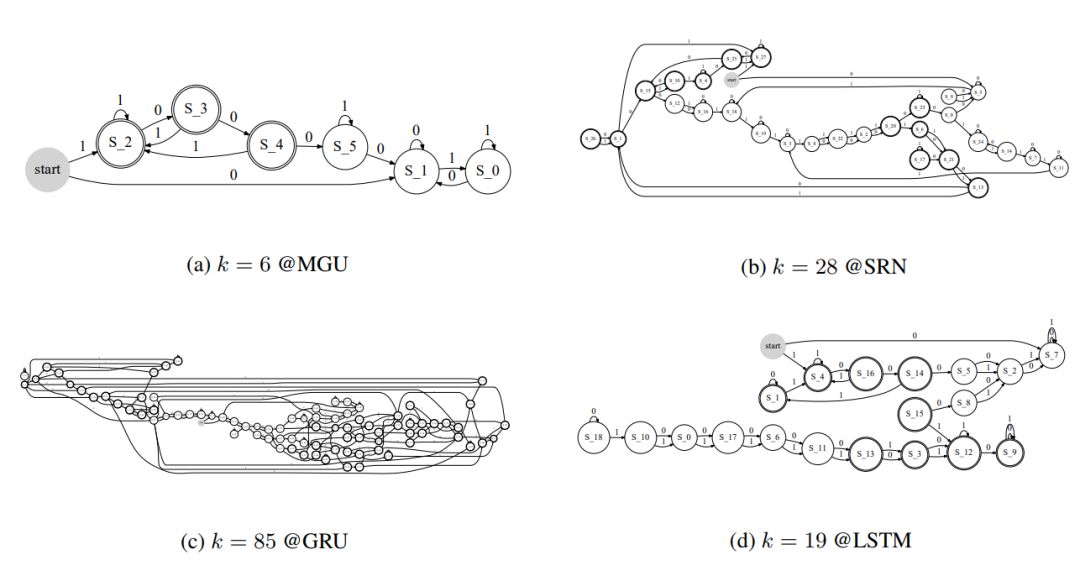
Figure 4: The structure diagram of the FSA learned when training 4 RNNs on Task “000”. The number of clusters k is determined by the clustering number when the FSA first reaches an accuracy of 0.7.

Figure 7: The FSA learned from MGU trained on the sentiment analysis task. The FSA here is compressed, and words between the same two states in the same direction are grouped into the same word class. For example, words in the “word class 0-1” all represent transitions from state 0 to state 1.

Table 5: Words transitioning from state 0 are called acceptable states (i.e., states 1 containing positive movie reviews), where most words are positive. The numbers in parentheses indicate the FSA number from which the words originate.
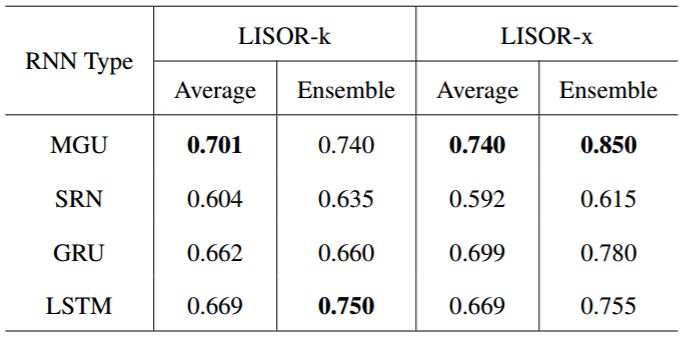
Table 4: The accuracy of sentiment classification tasks when the number of clusters is 2.

Recommended Reading
Andrew Ng’s “Machine Learning Yearning” Chinese version
My Deep Learning Introduction Path
My Machine Learning Introduction Roadmap

