The following notes summarize key points from the second week of the first part of Andrew Ng’s “Neural Networks and Deep Learning” course in the DeepLearning.ai project on Coursera.
These notes do not cover all the details of the video lectures. For content omitted in these notes, please refer to Coursera or NetEase Cloud Classroom. It is strongly recommended to watch Andrew Ng’s video lectures before reading the notes below.
1 Binary Classification Problem

Shape of the target data:
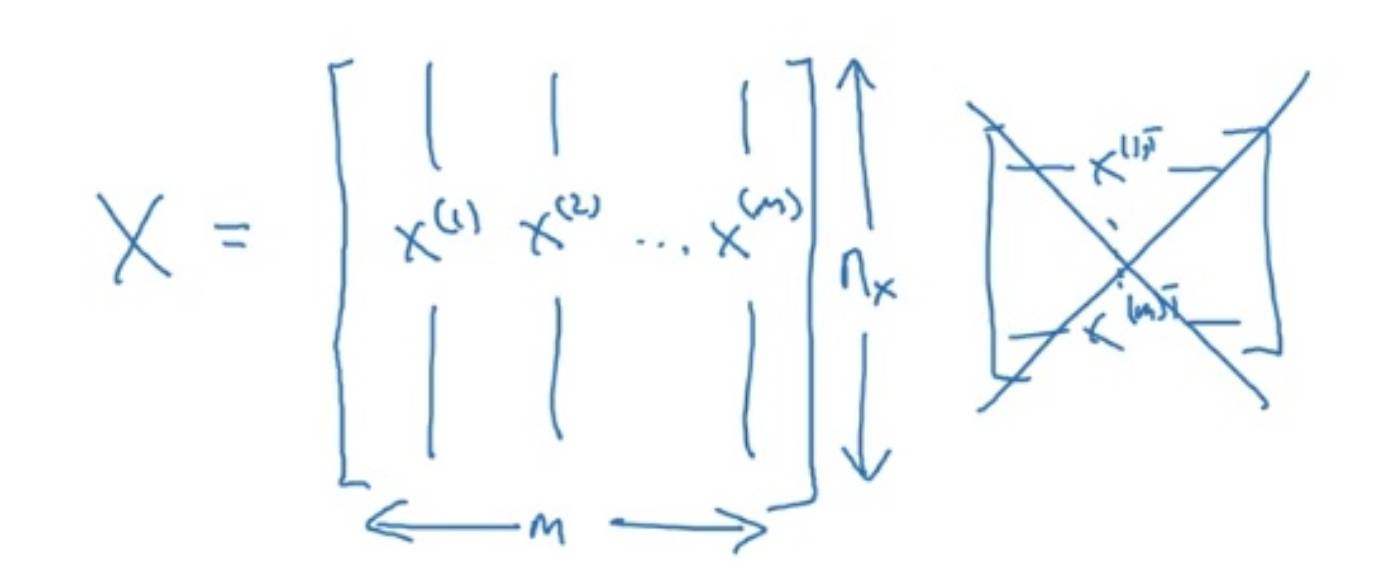

2 Logistic Regression

Note: The first derivative of the function can be expressed in terms of itself,

3 Logistic Regression Loss Function
Loss function
As a general rule, squared error is used to measure the Loss Function:
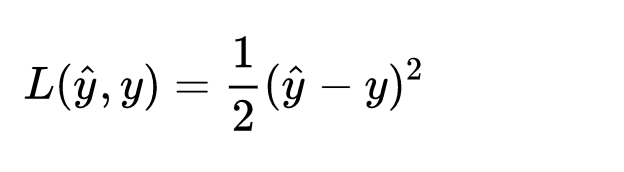
However, for logistic regression, squared error is generally not suitable as a Loss Function because the squared error loss function above is typically a non-convex function, which can lead to local optima rather than global optima when using gradient descent algorithms. Therefore, a convex function should be chosen.
The Loss Function for logistic regression:

Cost function
The average of the total Loss function across the entire training dataset is the cost function for the training set.
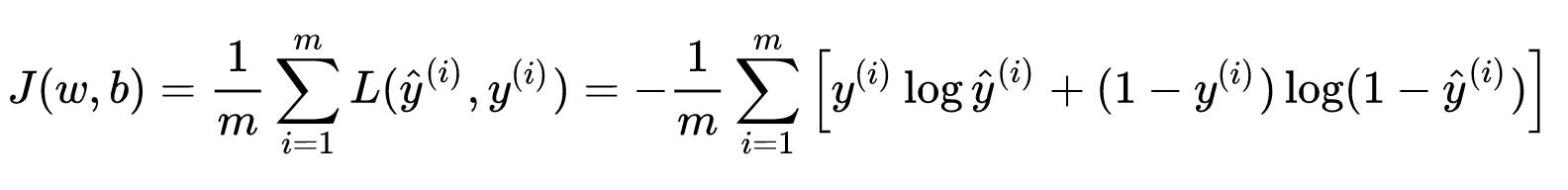
-
The cost function is a function of the coefficients w and b;
-
Our goal is to iteratively compute the optimal values of w and b, minimizing the cost function to get as close to 0 as possible.
4 Gradient Descent

5 Gradient Descent in Logistic Regression
For a single sample, the expression for the logistic regression Loss function:
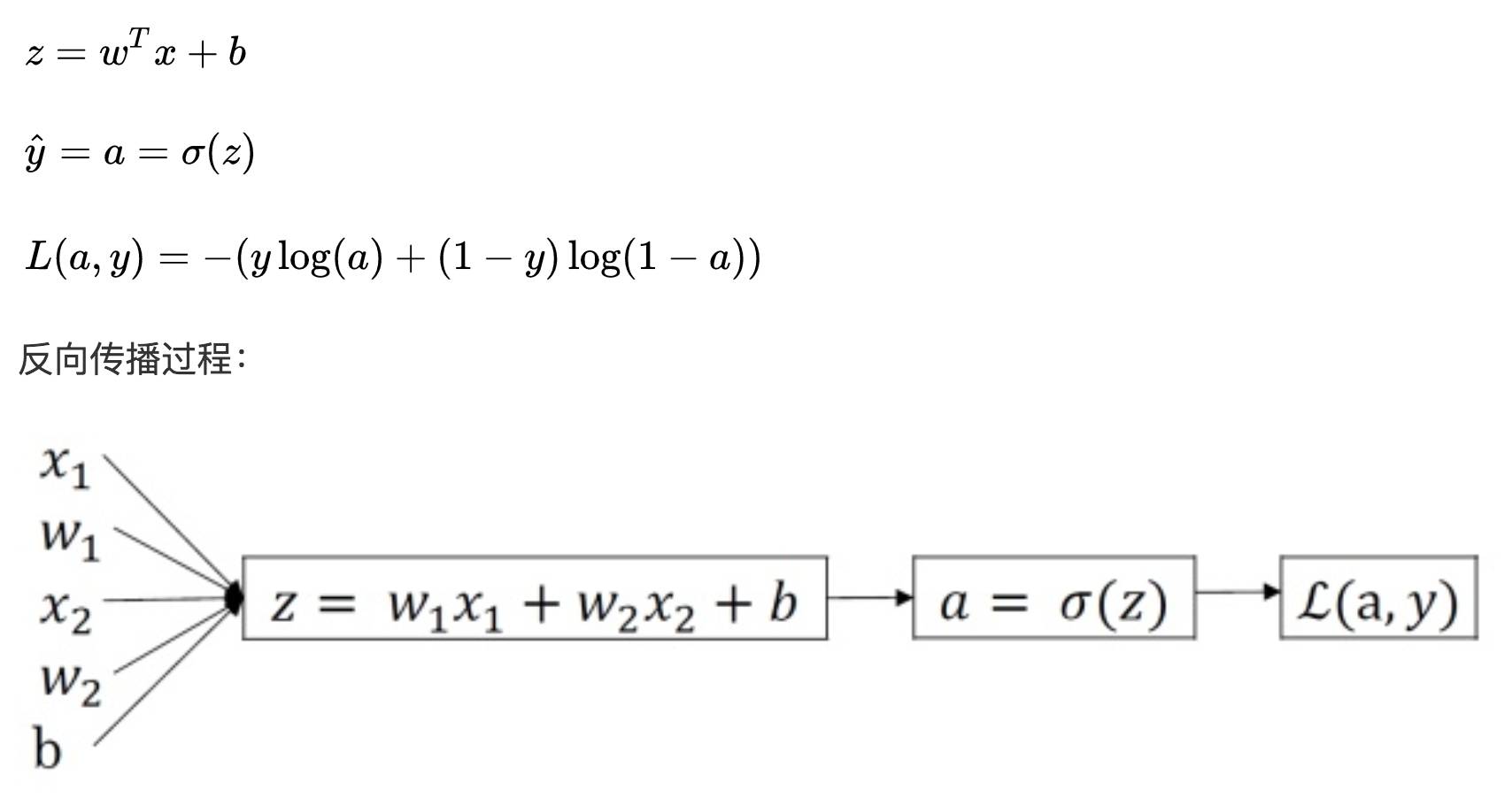


6 Gradient Descent for m Samples

7 Vectorization
In deep learning algorithms, we often have a large amount of data. During programming, we should minimize the use of loop statements as much as possible, using Python to perform matrix operations to improve program execution speed and avoid using for loops.
Vectorization in Logistic Regression

Python code:
db = 1/m*np.sum(dZ)Single iteration gradient descent algorithm process
Z = np.dot(w.T,X) + b
A = sigmoid(Z)
dZ = A-Y
dw = 1/m*np.dot(X,dZ.T)
db = 1/m*np.sum(dZ)
w = w - alpha*dw
b = b - alpha*db8 Python Notation
Although Python has a broadcasting mechanism, to ensure the correctness of matrix operations in Python programs, it is a good habit to use the reshape() function to set the required dimensions for matrix calculations;
If the following statement is used to define a vector, the generated dimension of a will be (5,), which is neither a row vector nor a column vector, and is called an array with a rank of 1. If a is transposed, it will yield a itself, which can cause issues in calculations.
a = np.random.randn(5)If you need to define a (5,1) or (1,5) vector, use the following standard statements:
a = np.random.randn(5,1)
b = np.random.randn(1,5)You can use the assert statement to check the dimensions of vectors or arrays. The assert statement checks the embedded statement, i.e., whether the dimension of a is (5,1). If not, the program stops here. Using the assert statement is also a good habit that helps us check and discover whether the statements are correct in a timely manner.
assert(a.shape == (5,1))You can use the reshape function to set the required dimensions for the array
a.reshape((5,1))9 Explanation of the Logistic Regression Cost Function
Origin of the Cost Function



Column: https://zhuanlan.zhihu.com/p/29688927
Recommended Reading:
Selected Essentials | Summary of Key Content in the Last Six Months
Essentials | Notes from the Machine Learning Foundations Course by National Taiwan University – Training versus Testing
Essentials | Detailed Notes from MIT Linear Algebra Course [Lesson 1]
Welcome to follow our public account for learning and communication~

Welcome to join our discussion group for learning and communication

