
Reference
Cohen G, Sapiro G, Giryes R. Detecting adversarial samples using influence functions and nearest neighbors[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020: 14453-14462.
Abstract
Deep neural networks are notorious for being vulnerable to adversarial attacks, which involve adding small perturbations to input images to mislead their predictions. Therefore, detecting adversarial samples is essential for the robustness of classification frameworks. In this work, we propose a method to detect such adversarial attacks that is applicable to any pre-trained neural network classifier. We use influence functions to measure the impact of each training sample on the validation set data. From the influence values (quantified), we identify the most reliable training samples for any given validation set. We search for sequences of these supporting training samples by fitting a k-NN (k-nearest neighbors) model to the activation layers of the DNN. We observe that these samples are highly correlated with the nearest neighbor points of normal inputs, whereas this correlation is much weaker for adversarial inputs. We trained an adversarial detector using the k-NN nearest neighbors and their distances, demonstrating that this detector can successfully distinguish adversarial instances and achieves state-of-the-art performance against six attack methods across three datasets. The code is open-sourced at https://github.com/giladcohen/NNIF_adv_defense.
Research Background
Deep neural networks (DNNs) are widely used in academia and industry, achieving state-of-the-art results in many domains, such as computer vision, natural language processing, and speech recognition. However, research shows that DNNs are vulnerable to adversarial samples, which are carefully designed perturbations to their input data that can deceive machine learning models, inducing them to make incorrect predictions with high confidence while remaining undetectable to humans. The adversarial subspaces of different DNN classifiers often exhibit overlapping phenomena, making it challenging to distinguish some adversarial samples generated by the model from other imperceptible DNNs. This renders adversarial attacks a genuine threat to any machine learning system.
The vulnerability of neural networks raises questions about their use in sensitive applications where adversaries might provide modified inputs to trigger misclassification. Consequently, many methods have been developed to address this adjustment, mainly divided into two categories: 1) proactive defense methods aimed at enhancing DNN robustness against adversarial samples; 2) reactive detection computations that do not alter the DNN but instead attempt to discover whether an attack is related to a given input.
In the realm of adversarial attacks and defenses, numerous researchers are conducting various related studies. Theoretically, Madry et al. adopted a robust optimization framework, demonstrating results of adversarial training; they found that projected gradient descent (PGD) is an optimal first-order adversarial method, which can yield optimal robustness against any first-order attack when used in DNN training. Simon-Ganriel et al. proved that the vulnerability of DNNs to adversarial attacks increases with the enhancement of the gradient of the training loss function. They also found that this vulnerability does not depend on the DNN model. Fawzi et al. studied the shape and complexity of the set of functions learned by DNNs and conducted empirical analyses on the curvature of decision boundaries. Their findings indicate that DNN classifiers are most vulnerable when the decision boundary is positively curved, while natural images typically lie near flat decision boundaries. These findings are also supported by Moosavi-Dezfooli et al., who discovered that positively curved decision boundaries increase the likelihood of deceiving DNN classifiers with small universal perturbations. Some works provide guarantees for the robustness of networks. Hein and Andriushchenko established a formal upper bound on the noise required for RNN network predictions, while Sinha et al. provided an efficient and fast robustness guarantee for worst-case performance.
Attacks based on Jacobian-based saliency map methods (JSMA) employ a different approach. This attack does not gently alter all image pixels but instead designs perturbations based on the L0 norm to find the maximum change caused by losing one or two pixels, modifying only those. This is a highly effective attack method, achieving success rates of up to 97%.
Moosavi-Dezfooli et al. highlighted Deepfoll as a non-targeted attack that creates adversarial examples by moving the attacked input sample to its nearest decision boundary. Carlini and Wagner proposed targeted attacks that affect defense distillation methods, and in another work, they provided an optimization framework that incorporates specific defense losses as a regularization term. Feinman et al. proposed an LR detector based on kernel density (KD) and Bayesian uncertainty features. Ma et al. described the dimensional properties of adversarial subspace regions and proposed a property known as local intrinsic dimensionality (LID). Papernot and McDaniel introduced the deep k-nearest neighbors (DkNN) algorithm to better estimate the predictions, confidence, and trustworthiness of given test samples. Lee et al. trained generative classifiers using DNN activations from each layer of the training set, applying confidence scores based on Mahalanobis distances to detect adversarial samples.
This Work
We use two “metrics” to examine the influence of training data on network decisions. The first is the influence function, which determines how data in the training set affects the network’s decision for a given test sample. This metric quantifies the impact of a small change in a specific training point on the loss of a test point within the loss function. Therefore, it provides us with a measure of the test sample, primarily used to classify the degree of influence of each training sample.
Secondly, we embedded k-NN in the network model space; various recent works have demonstrated a high correlation between the outputs of the network’s pooling layers and the k-NN decisions applied to the embedding space of that network. They essentially show that the network’s decisions depend on the similarity of the nearest neighbors in the embedded space. Thus, distances in this space can serve as a measure of the effectiveness of network outputs.
Considering the influence function and k-NN based metrics, we combine them to generate a new strategy for detecting adversarial examples. The fundamental principle behind our method is that for a normal input, its k-NN training samples and the most useful training samples should be correlated. However, for adversarial samples, this correlation should be disrupted, thus serving as a reference indication of an ongoing attack.
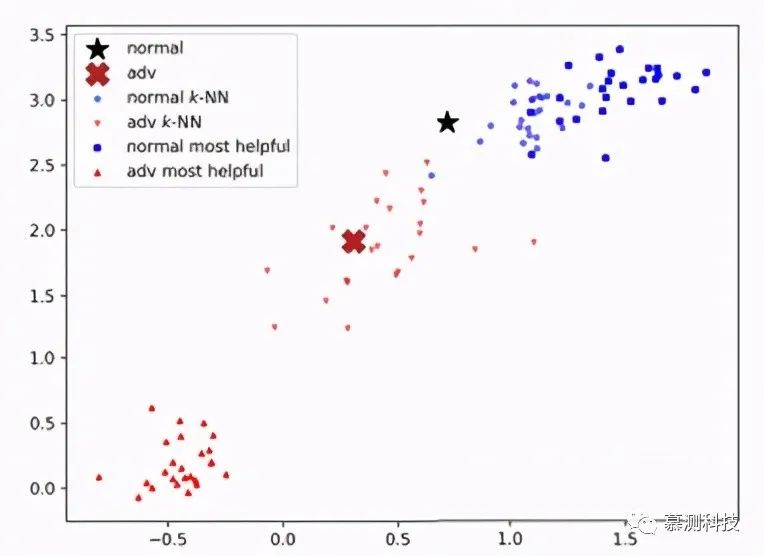
The above figure illustrates the relationship between k-NN and the most helpful training samples. The black stars and brown Xs represent normal images from the CIFAR-10 validation set and their corresponding adversarial images; for each sample, we find its 25 nearest neighbors in the DNN embedding space (blue circles/red downward triangles); additionally, we find 25 of the most useful training examples from the training set (blue squares and red upward triangles). Notably, in the PCA embedding space, the nearest neighbors of normal images and the most useful training samples are very close, whereas adversarial images do not exhibit the same correspondence among their training samples.
To examine the correlation between the two, we adopt the following strategy: for invisible input samples, we select the most influential samples from the training set using the influence function. However, we check their ranking in terms of distance in the network embedding space (and their L2 distance ranking with the input sample embedding vectors). Finally, we use these k-NN features to train a simple Logistic Regression (LR) model to detect whether the input is adversarial.
We evaluated our detection strategy across various attack methods and datasets, showing their advantages over other leading detection techniques. Experimental results confirm the earlier hypothesis regarding the similarity between k-NN applied to the embedding space and DNN decisions, illustrating how it is used to detect adversarial samples.
Research Methodology
We assume that DNN predictions are influenced by k-NN data in its hidden layers, particularly in the front. To deceive the network, adversarial attacks must move the test samples into the “bad” subspace of the embedding space, where erroneous training data can lead to incorrect classifications by the network. To test our hypothesis, we fit a k-NN model on the activation layers of the DNN and employed an influence function proposed by Koh and Liang.
The influence function can indicate which training samples contribute positively to DNN predictions and which do not. The expression for this influence function is as follows:
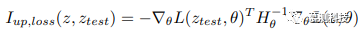
Where H is the Hessian in its learning model, L is the loss of its learning model, and θ are the model parameters.
For each test example Ztest, the influence values for each training sample in the training set are calculated according to the formula depicted above, and then the resulting I values are sorted to determine the top M most useful and harmful training examples for a specific Ztest. Next, for each selected 2×M training points, we find their ranks and distances to the test sample using a k-NN model fitted in the embedding space with all training samples’ embedding vectors. We input the embedding vector of each test sample Z into the k-NN model, extracting the nearest neighbor ranks (R) and distances (D) of all examples in the training set, where RM’ and DM’ are all harmful training samples. We repeat this process to create an efficient dataset.
We named our adversarial detection method the Nearest Neighbor Influence Function (NNIF). (Assuming that the training, validation, and test dataset is not contaminated with adversarial examples) we perform relevant validation on this sample. We primarily utilize NNIF features to train an LR classifier, partitioning its output values into positive and negative based on the harmful/useful classification: adversarial (positive) and normal (negative).
For the reliability and robustness of DNNs, they utilize nearest neighbor values in the activation layers to achieve interpretability. As a new competitive strategy, we transform the original DkNN algorithm into an adversarial detection method. This is accomplished by collecting empirical p-values computed in the DkNN strategy and specifying a reactive adversarial detector by training an LR model on these features. Although NNIF also uses nearest neighbor values, we do not check the labels of the nearest neighbors but instead use the influence function to examine their correlations with the most beneficial/harmful training samples.
Experimental Results
We compared the performance of NNIF against SOTALID, the Mahalanobis detector, and the DkNN adversarial detector, demonstrating our NNIF adversarial detector’s capabilities against six adversarial attack strategies. Finally, we analyzed the robustness of NNIF under white-box testing. Before presenting our results, we first describe the experimental setup used in our analysis.
Ø Experimental Setup
Training and Testing: Three image datasets were divided into three subsets: training set, validation set, and test set, containing 49k, 1k, and 10k images, respectively. The data sources are the official SVHN training set and SVHM test sample set.

Its algorithm flow is illustrated in the above figure. Based on the AUC values of the ROC curves observed, we used nested cross-validation within the validation set to select the noise amplitude for the DkNN, Mahalanobis methods, and the top influence samples needed to be collected by NNIF. We optimized the deep k-nearest neighbors using grid search. The entire execution process is contained in the pseudocode depicted in the above figure.
Ø Detecting Adversarial Attacks
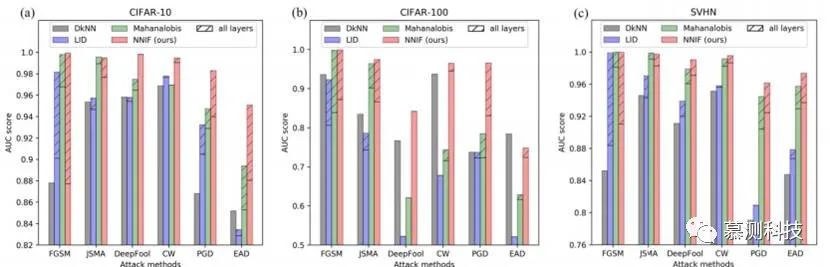
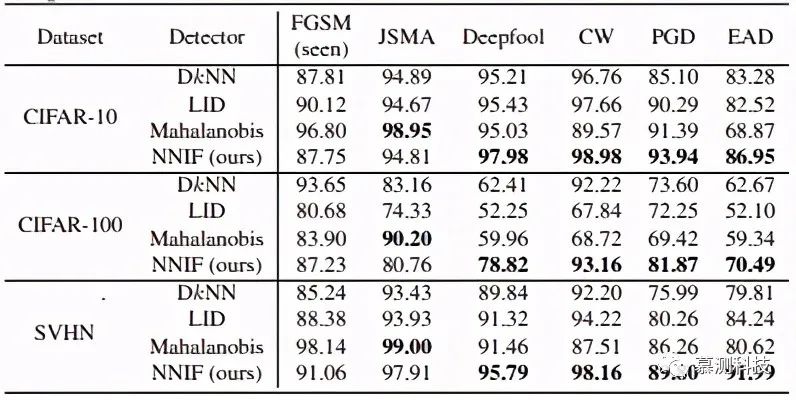
The above figure shows the recognition capabilities of four detection adversarial detectors: DkNN (black), LID (blue), Mahalanobis (green), and NNIF (red) on the CIFAR-10, CIFAR-100, and SVHN mainstream datasets. We compared the detection scores of six adversarial attacks: FGSM, JSMA, Deepfool, CW, PGD, and EAD. In some cases, considering all layers of DNN activation, the scores of LID/Mahalanobis/NNIF were enhanced, as depicted in the shadow pattern above.
It can be observed that our method outperforms all other detectors in distinguishing Deepfool, CW, and PGD attacks across all datasets. For FGSM and JSMA, our NNIF detector also demonstrates SOTA results, matching the performance of the Mahalanobis detector. For EAD, we show new SOTA results for CIFAR-10 and SVHN, but not for CIFAR-100.
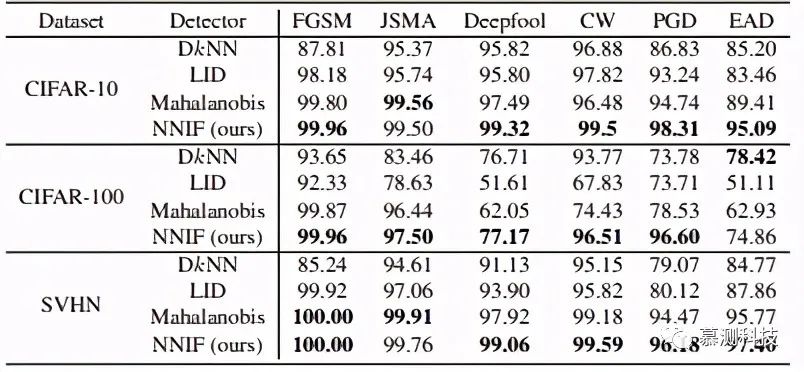
The above figure summarizes the AUC scores of all DNN activation layer features in the detectors, with the only exception being the DkNN method, which is used only in the embedding space.
Ø Validity Verification
Quantifying the contribution of each feature (RM’ DM’ RM’’ DM’’), we conducted a reliability study on the CIFAR-10 dataset. The following figure displays the AUC and accuracy results of Deepfool attacks using only DNN embedding space features.
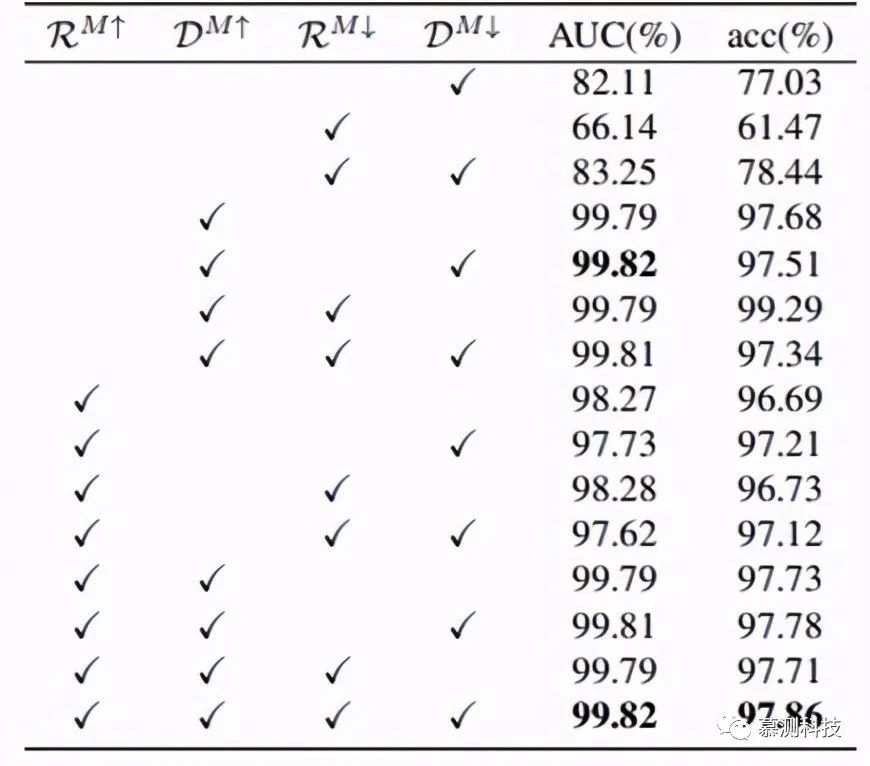
Our analysis indicates that the most influential feature is DM’, which represents the L2 distance to the most helpful training samples in the embedding space. We also demonstrated that the features RM’ DM’ DM’’ affect the attacks differently; we computed the probability density functions of these three features for Deepfool and CW attacks on CIFAR-10, concluding that RM or DM is more useful for detecting Deepfool adversarial attacks than CW. On the other hand, the DM’’ feature is better at distinguishing Deepfool attacks from CW attacks.
Deploying any learning-based detector is risky, as attackers might have access to the parameters of the LR classifier. Therefore, deploying a detector to detect a feature and applying a simple threshold is beneficial. Our results indicate that this scheme is possible for NNIF when using DM’ for all potential attack features.
Ø Application Expansion
To evaluate the extent to which our detection method can be transferred to unseen attacks, we used the LR classifier trained on features obtained from FGSM attacks. The AUC scores are shown in the figure below:
It can be observed that our NNIF method exhibits the best generalization across all adversaries except for JSMA.
Ø Attacking NNIF
To better validate the effectiveness of our proposed NNIF, we conducted an evaluation. Here, we considered a threatening white-box model, where the adversary is aware of all model information. We applied this white-box attack. The attack strategy is illustrated in the figure below:
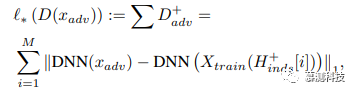
Here, DNN (·) represents the network transformation from the input image to the penultimate embedding vector, and Hinds+[i] is the index of the i-th most helpful training sample. c is a constant that balances the fidelity of the original image and the strength of the adversarial attack.
We applied this white-box attack to 4000 random samples from the ciremote-10 test set, comparing the performance of DkNN, LID, Mahalanobis, and NNIF detectors on the original CW against CW-opt attacks, with the experimental results shown in the figure below:
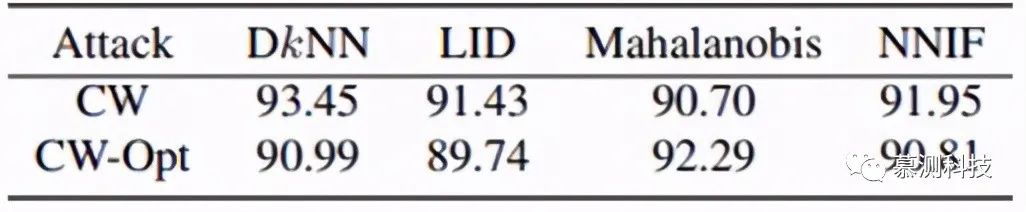
It can be observed that the proposed white-box attack only reduced the detection accuracy of NNIF by 1%, leading us to conclude that our NNIF defense algorithm is robust. However, we observe that the Mahalanobis value exhibited an increase, which is somewhat expected, as Mahalanobis estimates the global Gaussian distribution for each class without considering local features in the embedding space.
Conclusion
In this paper, we discussed the task of detecting adversarial attacks. Our research findings indicate that for original images in the DNN embedding space, their nearest neighbor values are strongly correlated with whether they are influenced by the influence function. Furthermore, the L2 distance of the test image embedding vector to its most helpful training input DM’ is a favorable measure for detecting adversarial samples. Using the aforementioned distances combined with the nearest neighbor ranking of training inputs, we achieved SOTA adversarial detection performance against six attacks (FGSM, JSMA, Deepfool, CW, PGD, EAD) across CIFAR-10, CIFAR-100, and SVHN datasets. Additionally, we demonstrated that our detector exhibits robustness under white-box testing.
A potential avenue for future research is to examine how different distance metrics, or transformations of DNN embedding vectors, relate to the most beneficial/harmful training samples. We emphasize that throughout our analysis, we primarily used L2 distances, leading us to suspect that employing another distance metric (such as Mahalanobis distance) might further enhance our experimental results.
Another open question for future research is the computational time, which requires reflecting the impact of the computational function across the entire training set. Clearly, optimizing computation time is a priority for deploying our NNIF algorithm, especially for real-time applications or systems that demand rapid detection capabilities. One possible solution to this problem is to establish a hash mapping relationship between the nearest and most influential training samples. Each training sample can be encoded with a probability vector to determine its impact on a specific class, and then the probabilities for each class can be averaged, deploying a simple k-NN search in the embedding space.
Acknowledgements
This paper was translated and summarized by He Jiawei, a master’s student from the School of Software, Nanjing University, Class of 2021.
Thanks to the National Key R&D Program (2018YFB1403400) and the National Natural Science Foundation (61003024, 61170067) for their funding.
