1. Introduction
2. Graph Neural Networks for Multimodal Graph Learning
3. Multimodal Graph Learning for Images
4. Multimodal Graph Learning for Language Datasets
5. Multimodal Graph Learning Applied to Scientific Discovery
6. Outlook
Artificial intelligence methods for graphs have achieved significant success in modeling complex systems, with applications ranging from dynamic networks in biology to interacting particle systems in physics. However, increasingly heterogeneous graph datasets require multimodal approaches to combine different inductive biases. Inductive bias refers to the preference or tendency of a learning algorithm towards certain types of hypotheses in machine learning, which helps the algorithm make inferences from the given training data. This bias can be based on the prior knowledge of the algorithm designer or can be a hypothesis about the structure of the problem space.
Learning on multimodal datasets is challenging because inductive biases may vary by data modality, and the graph may not be explicitly given in the input. To address these challenges, graph AI methods combine different modalities to leverage cross-modal dependencies through geometric relationships. Diverse datasets are integrated through graphs and fed into complex multimodal architectures, which are defined as image-intensive, knowledge-based, and language-intensive models. With the above classifications, we introduce a multimodal graph learning framework that utilizes it to study existing methods and provides guidelines for designing new models.
Graph-based deep learning technologies have achieved breakthroughs in biology, chemistry, physics, and social sciences. The main use of Graph Neural Networks is to learn representations of various graph components including nodes, edges, subgraphs, and entire graphs based on neural message passing strategies. The representations learned by Graph Neural Networks can be used for downstream tasks, including label prediction through semi-supervised learning, self-supervised learning, as well as graph design and generation. In most existing applications, datasets explicitly describe graphs represented by nodes, edges, and additional information, which represent contextual knowledge such as the attributes of nodes, edges, and graphs.
Modeling complex systems requires data that observes the same objects from different perspectives, different scales, or through various modalities (such as images, sensor readings, language sequences, and concise mathematical statements). Multimodal learning studies how to optimize these heterogeneous complex observations to create learning systems that are widely applicable, robust to variations in the underlying data distribution, and can be trained with less labeled data. Although multimodal learning has succeeded in cases where single-modal methods fail, it still faces challenges in applying to a broader range of AI scenarios. These challenges include finding representation methods suitable for machine learning analysis and integrating combined information from different modalities to create predictive models. These challenges have proven to be difficult. For example, multimodal methods often focus only on the most helpful part of the modality during model training, neglecting other modalities that may have informational value – this defect is known as modality collapse. Additionally, contrary to the general view that “each object must exist in all modalities”, due to limitations in data collection and measurement techniques, the set of objects appearing in each modality may be small – this defect is known as missing modalities. Since different modalities can lead to complex relational dependencies, simple modality fusion cannot fully leverage multimodal datasets. Graph learning models connect different modality data points as edges in optimally defined graphs and construct learning systems suitable for various tasks to model the aforementioned data systems.
We explore a technique framework known as multimodal graph learning (MGL). Multimodal graph learning provides a framework that can encompass existing algorithms and assist in developing new methods that utilize graphs for multimodal learning. This framework allows for learning representations of fused graphs and studies how to address the aforementioned challenges of modality collapse and missing modalities. We apply the multimodal graph learning framework to a wide range of fields, from computer vision and language processing to natural sciences (Figure 1). This paper considers using image-intensive graphs (IIGs) for image and video reasoning, language-intensive graphs (LIGs) for processing natural and biological sequences, and knowledge-intensive graphs (KIGs) for assisting scientific discovery.
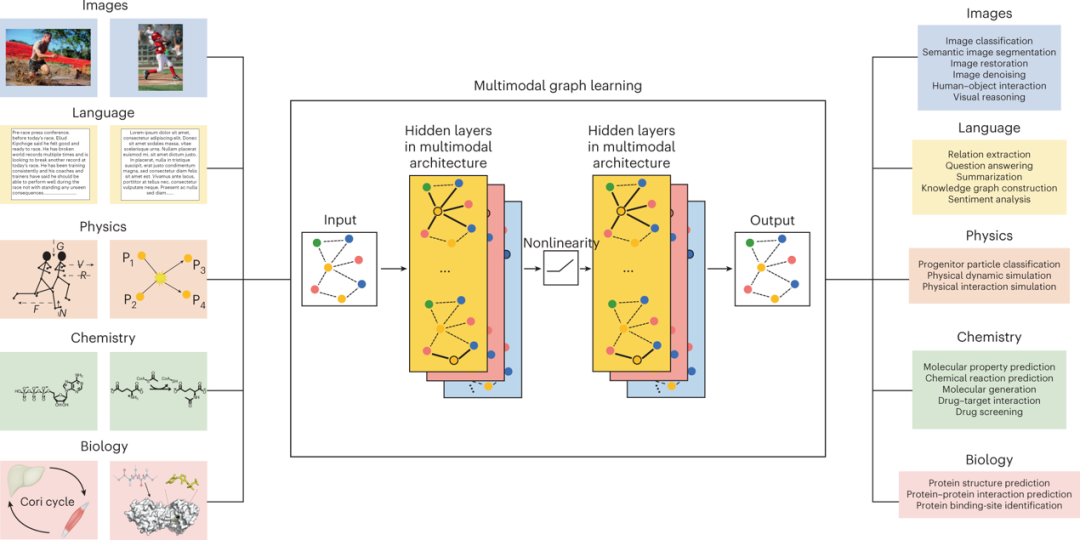
Figure 1 Centered multimodal learning. The left side shows different data modalities. The right side shows the value of multimodal graph learning in machine learning tasks. As a unified framework, multimodal graph learning achieves multimodal graph neural architectures through learning systems in computer vision, natural language processing, and natural sciences.
2. Graph Neural Networks for Multimodal Graph Learning
Deep learning has pioneered numerous fusion methods for multimodal learning. For example, the structure of Recurrent Neural Networks (RNN) successfully combines with Convolutional Neural Networks (CNN) for fusing audio and image information in video description tasks. Recently, generative models have also proven to be very accurate on language-related and physics-based multimodal data. These models are based on an encoder-decoder framework, where the combined architecture is trained simultaneously in the encoder (each architecture is specialized for one modality), while the decoder gathers information from each architecture. When complex relationships between modalities form a network structure, Graph Neural Networks (GNNs) provide an expressive and flexible strategy to leverage interdependencies in multimodal datasets.
The application of Graph Neural Networks in multimodal learning is attractive because they can flexibly model interactions within different data types and across types. However, data fusion through graph learning requires constructing network topologies and implementing inference algorithms on the graph. We propose a methodology that generates output representations suitable for downstream tasks based on given multimodal input data, which is integrated multimodal graph learning. The multimodal graph learning framework can be seen as consisting of four interconnected learning components that form an end-to-end flow. Figures 2a and 2b highlight the differences between traditional single-modal architecture combinations that handle multimodal data and our proposed integrated multimodal architecture.
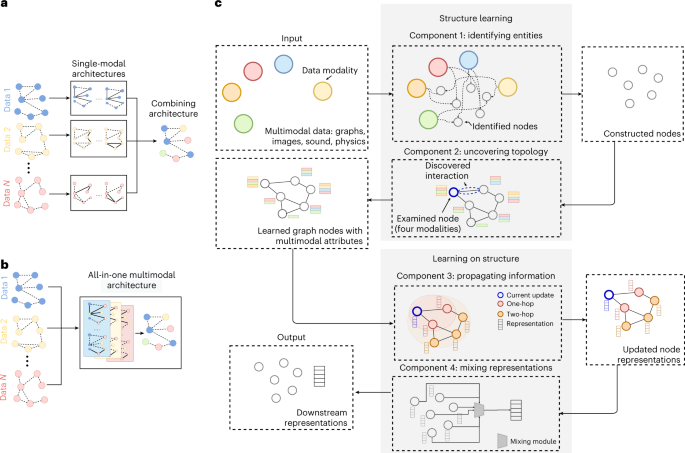
Figure 2 Architecture of multimodal graph learning. a, The conventional approach to multimodal learning is to combine different single-modal architectures, each optimized for a specific data modality. b, In contrast, the integrated multimodal architecture considers the unique inductive biases of each data modality and optimizes model parameters in an end-to-end manner to achieve data fusion at the representation level. c, Multimodal graph learning consists of four components: entity recognition, topology discovery, information propagation, and representation mixing. These components are divided into two stages: “structure learning” and “learning on the structure”.
The first two components of multimodal graph learning, namely entity recognition and topology discovery, can be categorized under the structure learning stage (Figure 2c).
(1) Component One: Entity Recognition
The first component of multimodal graph learning is used to identify relevant entities in various data modalities and project them into a shared naming space. For example, in precision medicine, a patient’s condition may be described through matched pathological slices and clinical notes, resulting in patient nodes with both image and language information. In another example from computer vision (Figure 3), entity recognition involves defining superpixels in an image.
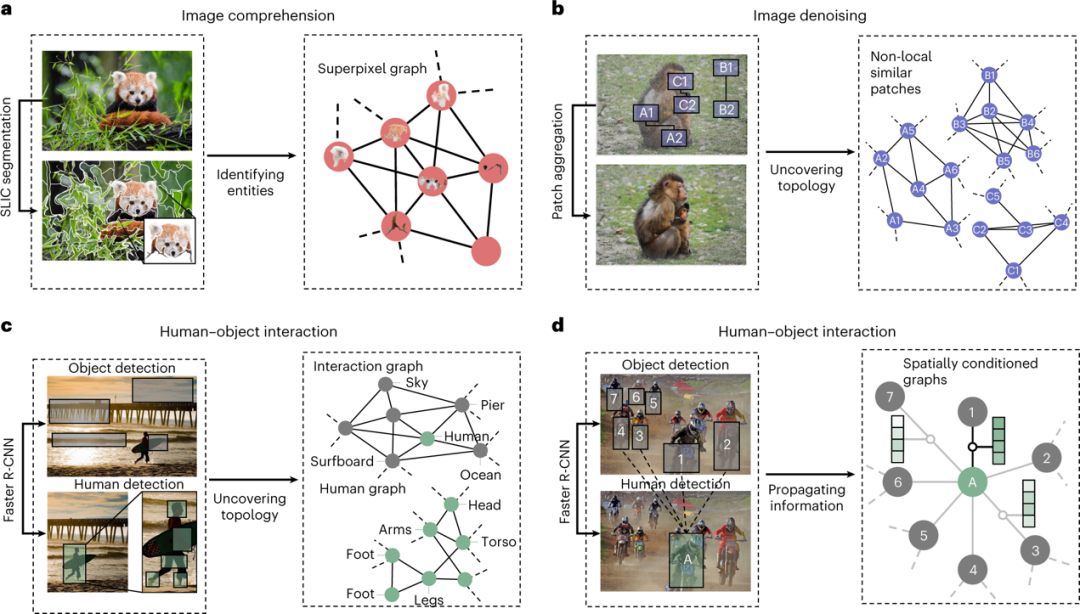
Figure 3 Applying multimodal graph learning in the image domain. a, Modality recognition in image understanding, where nodes represent regions of interest generated by the SLIC (Simple Linear Iterative Clustering) segmentation algorithm, also known as superpixels. b, Topology discovery in image denoising, where image patches (nodes) are connected to other non-locally similar patches. c, Topology discovery in human-object interaction, where two graphs are created. One human-centered graph maps body parts to their anatomically adjacent positions, while another graph connects body parts based on their distances relative to other objects in the image. d, Information propagation in human-object interaction, where a space-based graph modifies message passing to align the relative orientations of objects in the image based on edge features.
(2) Component Two: Topology Discovery
After defining the entities of the problem, the second component begins to explore interactions and types of interactions between cross-modal nodes. Interactions are often explicitly given, so they can be viewed as the graph being pre-defined, and this component is responsible for combining the existing graph structure with other modal structures (for example, in Figure 5c, the “topology discovery” part corresponds to combining protein surface information with the protein structure itself). When data lacks a preset network structure, revealing topological components explores possible adjacency matrices based on explicit features (e.g., spatial and visual features) or implicit features (e.g., similarity in representations). For the latter case, an example from natural language processing is considering constructing a graph from text input that expresses relationships between words (Figure 4b).
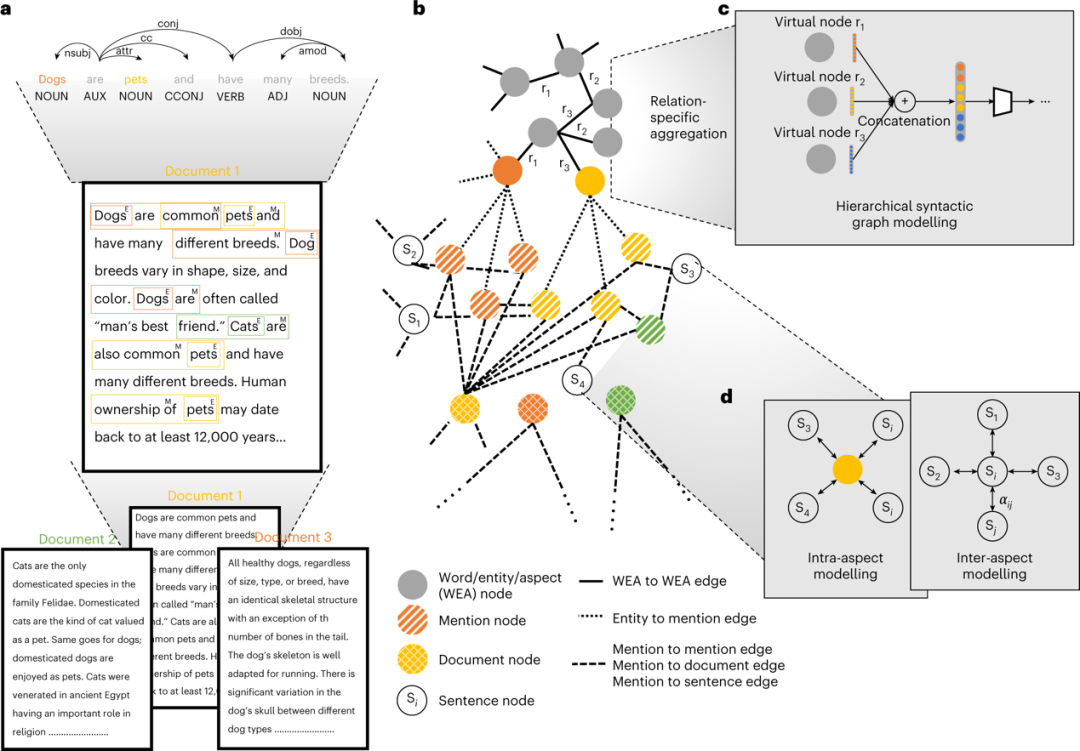
Figure 4 Applications of multimodal graph learning on language datasets. a, Different contextual background levels in text input, from sentences to documents and individual components identified within each context level. This is an example of the first component “entity recognition” in the multimodal graph learning framework. b, A simplified construction of language-intensive graphs from text input, which is an application of the “topology discovery” component in the multimodal graph learning framework. c and d are examples of “Aspect-Based Sentiment Analysis” (ABSA), which aims to provide sentiment scores for sentences given aspects, categorized as positive, negative, or neutral. By grouping within sentences based on their domains (c) or modeling the relationships between sentences and domains (d), these methods integrate inductive biases associated with aspect-based sentiment analysis and innovate in the third component of multimodal graph learning, “information propagation”.
Once the graph is specified or adaptively optimized (the structure learning stage in multimodal graph learning; Figure 2c), various strategies can be used for learning on the graph. The last two components of multimodal graph learning, collectively referred to as the “learning on the structure” stage (Figure 2c), describe these strategies.
(3) Component Three: Information Propagation
The third component uses convolution or message passing to learn node representations based on the adjacency relationships of the graph. In cases with multiple adjacency matrices, the method uses independent propagation models or assumes a hypergraph form to fuse the adjacency matrices with a single propagation model.
(4) Component Four: Representation Mixing
The final component transforms the learned node-level representations according to the needs of downstream tasks. The information propagation model outputs representations of nodes that can be mixed and combined based on the final representation levels (e.g., at the graph level or subgraph level labels). Popular mixing strategies include simple aggregation operations (such as summation or averaging) or more complex functions containing neural network architectures. Figure 2c shows all multimodal graph learning components, from multimodal input data to representations optimized for downstream tasks.
3. Multimodal Graph Learning for Images
Image-intensive graphs (IIGs) are a type of multimodal graph where nodes represent visual features, and edges represent spatial connections between image features. Structured image learning involves creating image-intensive graphs to encode geometric prior conditions related to images, such as translation invariance and scale separation. Translation invariance describes the property of convolutional neural networks where the output remains unchanged with input image displacement, achieved through convolution filters with shared weights. In contrast, scale separation indicates how to decompose long-range interactions across scale features, focusing on local interactions that can propagate to coarser-grained scales. For example, in convolutional neural networks, pooling layers immediately following convolutional layers achieve scale separation. Additionally, Graph Neural Networks can simulate long-range dependencies of arbitrary shapes that are critical for image-related tasks, such as image segmentation, image restoration, or human-object interaction.
Visual understanding remains central to visual analysis, and multimodal graph learning has proven to be significantly effective in image classification, segmentation, and enhancement. The task of image classification is to identify various objects present in an image. In contrast, image segmentation divides an image into several parts and assigns each part to a specific category. Finally, image restoration and denoising transform low-quality images into high-definition versions. The information required to accomplish these tasks includes objects, segments, and image patches, as well as their surrounding long-range contextual information.
The construction of image-intensive graphs (corresponding to components 1 and 2 of multimodal graph learning) begins with segmentation algorithms such as Simple Linear Iterative Clustering to determine meaningful regions (as shown in Figure 3a). These regions determine the nodes used for extracting feature maps and visual feature summaries of each region, with attributes initialized by convolutional neural networks such as FCN-16 or VGG19. Furthermore, nodes not only connect to their k nearest neighbor nodes in the feature space learned by convolutional neural networks (as shown in Figure 3b) but also connect to spatially adjacent regions or connect to any number of neighboring nodes determined by a pre-set similarity threshold between nodes.
Once the structure learning stage of multimodal graph learning is completed, propagation models based on graph convolution and graph attention (i.e., component 3 of multimodal graph learning) will weigh the neighbors of nodes in the graph according to the learned attention scores. Additionally, methods such as graph denoising networks, internal graph neural networks, and residual graph convolutional networks will consider edge similarities to represent the relative distances between image regions.
Visual reasoning extends deep beyond merely recognizing visual elements; it unfolds reasoning by querying relationships between entities in an image. These relationships may involve interactions between humans and objects, such as human-object interaction, or more broadly, interactions between visual, semantic, and digital entities, as seen in visual question answering.
In human-object interactions, multimodal graph learning methods identify two entities, namely body parts (such as hands, faces, etc.) and objects (such as surfboards, bicycles, etc.), which interact in a fully connected bipartite graph or in a partially connected topological structure. In visual question answering tasks, multimodal graph learning methods construct a new topological structure that encompasses the interconnections between visual, semantic, and digital graphs. These entities include visual objects identified by extractors (such as Faster R-CNN) and scene text recognized by optical character recognition and digital text recognition. The interactions between these entities are defined based on spatial positioning: entities that are close together are connected by edges.
Based on the aforementioned structure learning (component 3 of multimodal graph learning), the way information is propagated between the same type of entities and different types of entities is distinguished. In human-object interactions, the same type of entities (i.e., intra-class neural information) exchange knowledge by following edges and applying transformations defined by graph attention, which weight the neural information based on the similarity of node latent vectors. In contrast, information between different types of entities (i.e., inter-class neural information) is propagated through graph parsing neural networks, where the weights are learned adaptively. The model may have multiple channels for reasoning same-class entities and sharing information across classes. For example, in human-object interactions, the relationship parsing neural network uses a dual-channel model to perform human-centered and object-centered message passing before the final prediction (Figure 3c). The visual question answering task also employs the same strategy, where visual, semantic, and digital channels independently perform message passing before sharing information through visual-semantic aggregation and semantic-digital aggregation. Other neural architectures can also serve as alternatives to graph-based channels.
4. Multimodal Graph Learning for Language Datasets
Language models have widely transformed our analysis of natural language with their ability to generate context language embeddings. However, beyond vocabulary, the structure of language also exists at the sentence level (syntactic trees, dependency parsing), paragraph level (inter-sentence relationships), and document level (inter-paragraph links). Mainstream language models such as Transformers can capture such structures, but they have strict computational and data requirements. Multimodal graph learning methods alleviate these problems by incorporating language structures into the model. Specifically, these methods rely on language-intensive graphs (LIGs), in which nodes represent semantic features connected by linguistic dependencies.
(1) Creating Language-Intensive Graphs
At the highest level of abstraction, language datasets can be viewed as a corpus consisting of a set of documents, followed by individual documents, a set of sentences, a set of entities, and finally individual words (Figure 4a). Multimodal graph learning can consider these different levels of contextual information by constructing language-intensive graphs. The choice of context to include and how to create language-intensive graphs to represent the context depends on the specific task requirements. We will describe the steps for text classification and relation extraction, as these tasks are foundational to most language analysis.
In text classification tasks, the model needs to assign appropriate labels to a piece of text based on the usage and meaning of words (tokens). The graph structure between words is determined by their relative positions in the document or co-occurrence relationships. Relation extraction seeks to identify relationships between words in the text, which is crucial for other language processing tasks (such as question answering, summarization, and knowledge graph reasoning). To capture the semantics of sentences, the structure between word entities is based on the underlying dependency trees. In addition to words, other entities are included to capture topological structure information across sentences (Figure 4a, b).
(2) Learning Language-Intensive Graphs
Once language-intensive graphs are constructed, we need to design a model that can learn on this graph and incorporate inductive biases relevant to specific language tasks. We take “Aspect-Based Sentiment Analysis (ABSA)” as an example to reveal how to learn on language-intensive graphs. Aspect-Based Sentiment Analysis associates the sentiment (positive or negative) of the text with a word, phrase, or topic. To perform the aspect-based sentiment analysis task, the model must understand the syntactic structure and explore long-distance relationships between topic words and other words in the text. To propagate information between distant words, domain-specific graph neural networks mask non-topic vocabulary in the language-intensive graph to achieve long-distance information propagation. They also perform element-wise multiplication (the multiplication of elements in the same position of two matrices or vectors to form a new matrix or vector) or gating processing (a mechanism in neural networks that controls the flow of information using “gates” to determine the extent to which information is retained or forgotten) on the latent representations of query words and topic words. To make the graph incorporate syntactic structure information, graph neural networks distinguish different types of relationships in the dependency tree through type-specific information propagation (Figure 4c).
When performing sentiment analysis on documents, the sentiment of adjacent or similar sentences is extremely important. Cooperative graph attention networks achieve this by collaboration between two graph model blocks – internal and external modules (Figure 4d). These modules capture the relationships between sentences and other sentences with the same topic (internal domain) as well as relationships with adjacent sentences containing different topics in the document (external domain). The outputs of the internal and external modules are mixed in an interactive module, passed through a series of hidden layers. Finally, the intermediate representations between each hidden layer are fused through learned attention weights to form the final sentence representation (component 4 of multimodal graph learning).
5. Multimodal Graph Learning Applied to Scientific Discovery
In addition to applications in computer vision and language modeling, the application of graphs in natural sciences is also increasing. We refer to these graphs as knowledge-intensive graphs (KIGs) because they incorporate inductive biases relevant to specific tasks or encode scientific knowledge in their structure.
(1) Multimodal Graph Learning in Physics
In particle physics, Graph Neural Networks have been used to identify source particles that lead to particle jets, which are produced by high-energy particle collisions and scatter outwards. In these graphs, nodes represent particles and are connected to their k nearest neighbor nodes. After multiple rounds of message passing, the aggregated node representations are used to identify source particles.
Physics-inspired Graph Neural Networks have emerged for simulating physical systems dominated by multi-scale processes. Traditional methods cannot handle such tasks. A typical goal is to discover hidden physical laws from existing experimental data. Graph Neural Networks train using existing experimental data and information by leveraging physical laws, and then evaluate at specific points in the spacetime domain. This physics-inspired architecture combines multimodal data with mathematical models. For example, Graph Neural Networks can represent differential operators of the underlying dynamics as functions on nodes and edges. Graph Neural Networks can also represent physical interactions between objects, such as particles in fluids, joints of robots, and nodes in power networks. Initial node representations describe the initial states of these particles and global constants such as gravity. Edges represent relative particle velocities. Message passing first updates edge representations and calculates the effects of forces within the system. Then, the updated edge representations are used to update node representations and compute the new states of particles after force application (Figure 5a). This message passing strategy advances the “multimodal graph learning for images” and has also been used to solve combinatorial algorithms (Bellman-Ford and Prim algorithms) and chip layout to design the physical layout of computer chips.
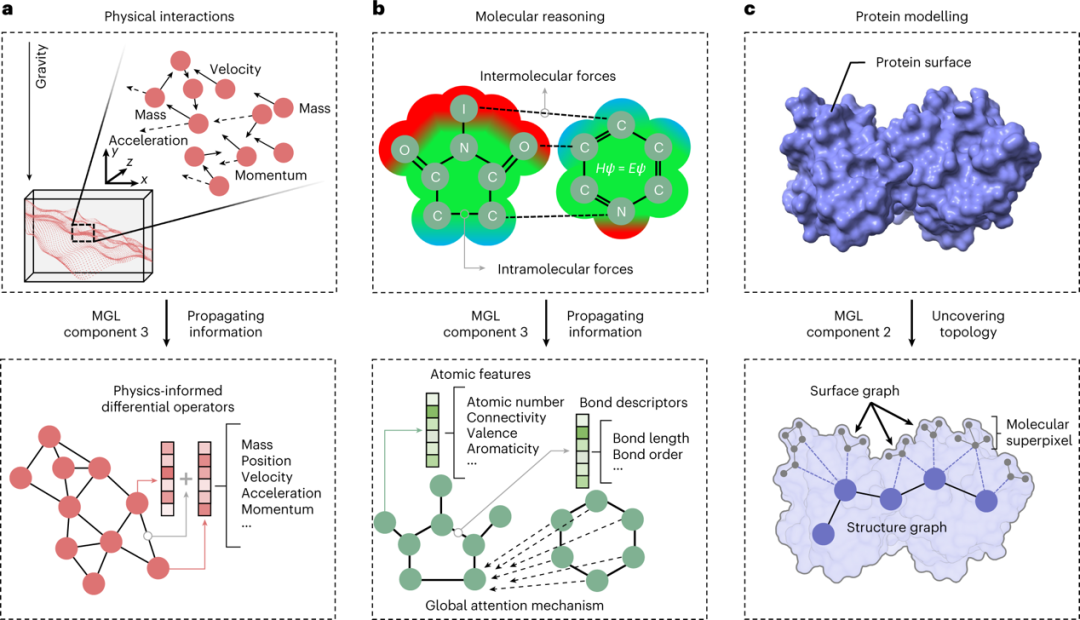
Figure 5 Applications of multimodal graph learning in natural sciences. a, Physics-inspired neural message passing networks update the states of particles in the system by propagating information through interactions between particles and other forces. b, Information propagation in molecular inference, utilizing global attention mechanisms to simulate potential interactions between atoms in two molecules to predict whether the two molecules will react. c, Topological structure discovery in protein modeling, utilizing multi-scale graph representations to combine the primary, secondary, and tertiary structures of proteins with higher-level protein motifs in molecular superpixels to represent a protein. This robust topological structure provides better predictive capabilities for tasks such as predicting protein-ligand binding affinities.
(2) Multimodal Graph Learning in Chemistry
In chemistry, multimodal graph learning can predict the internal and interaction properties of molecules by performing message passing operations on molecular graphs composed of atoms connected by chemical bonds. Current research work incorporates not only two-dimensional molecular details but also three-dimensional spatial molecular information. When such information is unavailable, multimodal graph learning considers not only granular atomic representations but also stereochemical features to aggregate neural information and represent molecules as collections of chemical substructures.
Stereoisomers are those with the same graph connectivity but different spatial arrangements of molecules. This means that the aggregation function in the molecular graph performs the same aggregation regardless of the orientation of atoms in three-dimensional space. This can lead to performance degradation because stereoisomers may have different properties. To address this issue, researchers have proposed two aggregation methods: permutation and permutation-connection. They update each atom within the group by calculating the weighted sum of all permutations of the chiral group. Although the identities of neighbors are the same in each permutation, their spatial arrangements differ. By weighting each permutation, permutation and permutation-connection successfully encode this inductive bias by modifying the way information is propagated in the underlying graph (component 3 of multimodal graph learning).
Additionally, multimodal graph learning can help determine the chemical products generated by reactions between molecules. For example, to predict whether two molecules will react, quantum-chemistry-enhanced Graph Neural Networks (QM-GNN) use initial representations of chemical information to represent the molecular graphs of each reactant. After multiple rounds of message passing, atomic representations are updated through global attention mechanisms (Figure 5b). This attention mechanism reveals a novel topological structure in which atoms can interact with atoms in other molecules. It integrates a chemical principle: the interactions between particles affect the chemical reaction itself. The final representation is combined with descriptors such as atomic charges and bond lengths and is used for prediction. This approach integrates structural knowledge about molecules in Graph Neural Networks with relevant chemical knowledge, allowing for accurate predictions on small training datasets. The fusion of Graph Neural Network outputs to include domain knowledge demonstrates the role of mixing modules in multimodal graph learning. Molecular graph learning creates new opportunities for virtual drug screening, molecular generation and design, and drug target identification.
(3) Multimodal Graph Learning in Biology
Not only for individual molecules, multimodal graph learning can also aid in understanding the properties of complex structures across multiple scales, with the most relevant being proteins. At the scale of amino acid sequences, the hallmark task is to predict the 3D structure from amino acid sequences. AlphaFold constructed a knowledge-intensive graph where nodes are representations of amino acids derived from sequence homology. To propagate information in this graph, AlphaFold introduced triangular multiplication updates and triangular self-attention updates. These triangular modifications integrate the inductive bias that learned representations must obey the triangle inequality of distances to represent 3D structures. Innovations such as multimodal graph learning enable AlphaFold to predict 3D protein structures from amino acid sequences.
In addition to 3D structures, the geometric and physical properties of protein surface molecules play a key role in cellular function and disease, making it crucial to model these properties. For example, MaSIF (a multimodal graph model for predicting protein interactions) trains a Graph Neural Network by describing molecular surfaces as multimodal graphs to predict protein interactions. The initial representations of nodes are based on geometric and chemical properties. Next, the Gaussian kernels defined for each node are used for information propagation to encode the complex geometric shapes of molecular surfaces, extending the concept of convolution. The final representations can be used to predict protein-protein interactions, structural configurations of protein complexes, and binding of proteins to ligands.
Multimodal graph learning is an emerging field with applications spanning natural sciences, vision, and language domains. We anticipate that comprehensive multimodal graph architectures and their new applications in natural sciences and medicine will drive the development of multimodal graph learning. At the same time, we outline when multimodal graph learning may prove to be of little value or useless, and the need for improvement to address challenges arising from multimodal inductive biases or explicit lack of graph structures.
(1) Comprehensive Multimodal Graph Architectures
Current mainstream methods mainly adopt domain-specific architectures tailored for various data modalities. However, the advancement of universal architectures provides a representation strategy that considers the interdependencies between modalities, regardless of whether they are presented as images, language sequences, graphs, or tabular datasets. Furthermore, multimodal graph learning architectures support more complex graph structures, such as hypergraphs and heterogeneous graphs.
This architecture also paves the way for new applications of graph-based multimodal learning. For example, knowledge distillation aims to transfer knowledge from a large “teacher” model to a smaller “student” model while maintaining performance and using fewer resources. Knowledge-intensive graphs can be used to design more efficient knowledge distillation loss functions. In another case, visible neural networks set the architecture so that nodes correspond to concepts at different scales of cellular systems (such as molecules, pathways), connected based on biological relationships and used for forward and backward propagation. By integrating such inductive biases, models can be trained efficiently with data, as they do not need to reinvent relevant fundamental principles but understand these principles from the start, requiring less training data. Coordinating algorithm design with domain knowledge also helps improve the interpretability of models.
(2) Comprehensive Multimodal Graph Architectures
In fields lacking prior knowledge or relational structures, the application of existing methods is limited. For example, in tasks such as predicting chemical reactions, classifying jet source particles, simulating physical interactions, and protein-ligand modeling, task-relevant interactions are not pre-defined, meaning these methods must automatically capture novel, unspecified, and relevant interactions. Some applications adopt node feature similarities to dynamically construct local adjacency relationships after each layer to discover new interactions. However, since information is only propagated between closely connected nodes, this approach cannot capture novel interactions between distant nodes. A solution to this limitation is to introduce attention layers with induced sparsity to discover. In applications without strong correlation structures, such as molecular property prediction, particle classification, and text classification, node features often hold higher predictive value than any encoding structure. Therefore, some other methods have been shown to outperform graph-based methods in terms of performance.
(3) Pioneering Applications in Natural Sciences and Medicine
The application of deep learning in the natural sciences reveals the powerful capacity of graphical representations in modeling molecular structures from small to large scales. Integrating different types of data can bridge the gap between molecular and organism levels when simulating large-scale physical, chemical, or biological phenomena. Recent applications of knowledge graphs introduced into precision medicine and predictions in genomics, drugs, and clinics have emerged. Multiscale learning systems are becoming important tools in areas such as protein structure prediction, protein property prediction, and modeling biomolecular interactions. These methods can integrate mathematical descriptions of physical relationships, knowledge graphs, prior distributions, and constraints by modeling preset graph structures or modifying message passing algorithms. When such information is present, multimodal learning can enhance performance in image denoising, image restoration, and human-object interaction within visual systems.
Graph Neural Networks and Combinatorial Optimization Reading Club
A large number of real-world problem solutions rely on the design and solving of algorithms. Traditional algorithms are designed by human experts, and as AI technology continues to develop, cases of algorithms learning algorithms are increasingly common, such as AI algorithms represented by neural networks, which is the reason for algorithm neuralization solving. In the direction of algorithm neuralization solving, Graph Neural Networks are a powerful tool that can fully utilize the characteristics of graph structures to achieve efficient approximations of high-complexity algorithms. Complex system optimization and control based on Graph Neural Networks will be a new future direction after the current trend of large models.
To explore the development and real applications of Graph Neural Networks in algorithm neuralization solving, the Intelligent Club, in collaboration with Associate Professor Fan Changjun from the School of Systems Engineering at the National University of Defense Technology and Associate Professor Huang Wenbing from the Gaoling Academy of Artificial Intelligence at Renmin University of China, jointly initiated the “Graph Neural Networks and Combinatorial Optimization” reading club. The reading club will focus on related areas of Graph Neural Networks and algorithm neuralization solving, including neural algorithm reasoning, solving combinatorial optimization problems, geometric graph neural networks, and the application of algorithm neuralization solving in AI for Science, aiming to provide participants with an academic exchange platform, stimulate participants’ academic interests, and further promote research and application development in related fields. The reading club will start on June 14, 2023, and will be held every Wednesday evening from 19:00 to 21:00, lasting approximately 8 weeks. Interested friends are welcome to sign up!
 For more details, please see:
Accelerating the Efficiency of Classic Algorithms, Breaking Through Real-World Technical Bottlenecks: The Launch of the Graph Neural Networks and Combinatorial Optimization Reading Club
For more details, please see:
Accelerating the Efficiency of Classic Algorithms, Breaking Through Real-World Technical Bottlenecks: The Launch of the Graph Neural Networks and Combinatorial Optimization Reading Club