In the process of constructing the detailed model structure of the twin neural network, we first create a shared convolutional network. We have already understood the convolutional layer, pooling layer, and fully connected layer.
First, please understand the following concepts:
Convolutional Layer
Pooling Layer
Convolutional Layer
Fully Connected Layer
Shared Convolutional Layer
Euclidean Distance
Let’s define a function and build the shared convolutional network based on the Sequential class: from keras.models import Sequential, Input from keras.layers import Conv2D, MaxPooling2D, Flatten, Dense
def create_shared_network(input_shape): model = Sequential() model.add(Conv2D(filters=128, kernel_size=(3, 3), activation='relu', input_shape=input_shape)) model.add(MaxPooling2D()) model.add(Conv2D(filters=64)) model.add(Flatten()) model.add(Dense(units=128)) return model
We can see that the above function creates a convolutional network based on the model structure. Now, you might be curious about how we share weights in two twin networks? The answer is that it is not necessary to create two completely independent networks; we only need to declare an instance of the shared network in Keras. We can use this instance to create two convolutional networks. Since it is a reuse of one instance, Keras knows to let them share weights. First, use the previously defined function to create an instance of the shared network: input_shape = X_train.shape[1:] shared_network = create_shared_network(input_shape) By using the Input class to specify inputs for the upper and lower layers: input_top = Input(shape=input_shape)
input_bottom = Input(shape=input_shape)
The next step is to stack the shared network on the right side of the input layer using Keras’s functional method, with the syntax as follows:
output_top = shared_network(input_top) output_bottom = shared_network(input_bottom) You might not be familiar with this syntax because we previously used the more user-friendly Sequential method to build models. Although using Sequential is simpler, it also loses some flexibility; some operations cannot be completed based on Sequential, such as building the above model structure. Therefore, we use the functional method to construct this model.
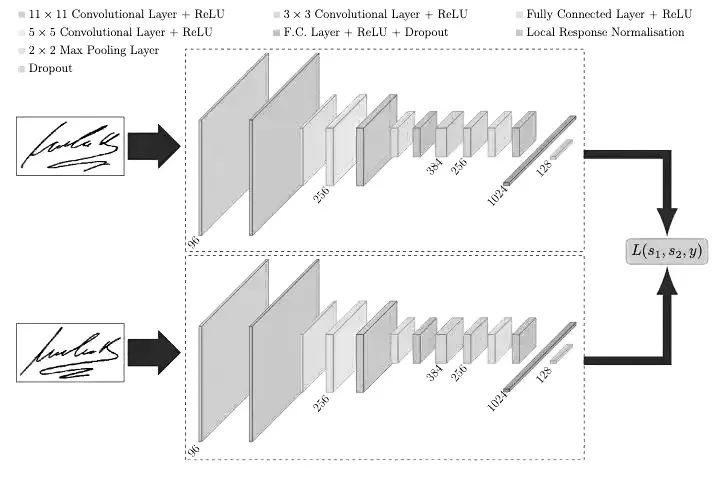
The next task is to merge the two outputs and then compute the Euclidean distance between them. Remember, the output result is a low-dimensional linear space represented by a 128×1 vector.
Since Keras does not have a layer that can directly compute the Euclidean distance, we must define it ourselves. By using the Lambda layer provided in Keras, we can encapsulate any function and define it as a layer object.
Define a euclidean_distance function to calculate the Euclidean distance between two vectors:
from keras import backend as K def euclidean_distance(vectors): vector1, vector2 = vectors sum_square = K.sum(K.square(vector1 - vector2), axis=1, keepdims=True) return K.sqrt(K.maximum(sum_square, K.epsilon()))
The euclidean_distance function can be encapsulated into a Lambda layer: from keras.layers import Lambda distance = Lambda(euclidean_distance, output_shape=(1,))([output_top, output_bottom])
Finally, merge the distance layer defined above with the inputs to form the complete model: from keras.models import Model model = Model(inputs=[input_top, input_bottom], outputs=distance)
Call the summary function to verify whether the model structure meets expectations:
print(model.summary())
The output result is shown in Figure 7-16.
Layer (type) input_1 (InputLayer) input_2 (InputLayer) Shared_Conv_Network (Sequential (None,128) Output Shape (None, 112, 92, 1) (None, 112, 92, 1)
Param
Connected to
0
18707264
input_1 [0] [0] input_2 [0] [0] Shared_Conv_Network [1] [0] Shared_Conv_Network [2] [0]
Euclidean_Distance (Lambda)
(None, 1)
0
Total params: 18,707,264 Trainable params: 18,707,264 Non-trainable params: 0
The model has two input layers, both of size 112x92x1. The two input layers are connected to a shared convolutional network. The two sets of outputs from the shared convolutional network (both 128-dimensional arrays) are merged and passed to the Lambda layer, which calculates the distance between the two 128-dimensional arrays. Finally, the computed Euclidean distance is used as the model’s output. That’s it! We have successfully created a twin neural network. As we can see, the complexity of the model mainly comes from the shared convolutional layers. With this basic structure, we can increase the complexity of the shared convolutional layers as needed.
