Graph neural networks (GNNs) have gained widespread attention and are applied in scenarios such as recommendation systems, knowledge graphs, and traffic analysis due to their advantages in handling non-Euclidean space data and complex features.
The irregularity of large-scale graph structures, the complexity of node features, and the dependency of training samples put immense pressure on the computational efficiency, memory management, and communication overhead of GNN models in distributed systems. This article first briefly introduces the message passing mechanism in GNN models, classifies common GNN models, and analyzes the difficulties and challenges faced in training with large-scale data; then it categorizes, summarizes, and analyzes GNN algorithm models aimed at large-scale data, including sampling algorithms based on nodes, edges, and subgraphs; next, it introduces relevant progress in accelerating GNN programming frameworks, mainly including an introduction to mainstream frameworks and a classification summary and analysis of optimization techniques.
Graph structures can describe complex relationships, such as gene structures, communication networks, traffic routes, and social networks. Graph computation extracts structural information but cannot learn node features. Neural networks perform well on Euclidean space data but cannot be directly applied to non-Euclidean space graph data. GNNs combine the advantages of graph computation and neural networks to handle non-Euclidean space data and its complex features, applied in scenarios such as network link prediction, recommendation systems, and traffic analysis. In practical applications, graph data can be enormous, with hundreds of billions of nodes and trillions of edges, with storage costs exceeding 10TB. GNNs face challenges in computational efficiency, memory management, and distributed communication overhead in large-scale data. The challenges faced by GNN models in large-scale data applications can be categorized into graph data structure, GNN models, data scale, and hardware platforms.
(4) Hardware Structure.GNN models have modeling needs regarding graph data structures and complex features, requiring flexible irregular data reading and efficient dense computation. CPUs and GPUs have their advantages but cannot satisfy both requirements simultaneously, increasing the difficulty of accelerating large-scale GNN models.
To improve the scalability of GNN models, accelerate the running process, and reduce memory overhead, researchers have proposed strategies to enhance GNN processing efficiency in application models for scenarios such as natural language processing, traffic prediction, and recommendation systems. In terms of algorithm models, to address memory issues, researchers have adopted mini-batch training, such as GraphSage and FastGCN. In programming frameworks, to solve the dependency of training samples, frameworks like DGL and PyG have been proposed. In terms of hardware structures, optimization strategies or dedicated hardware acceleration structures, such as HyGCN, have been proposed by combining CPUs, GPUs, FPGAs, etc. As shown in Figure 1:
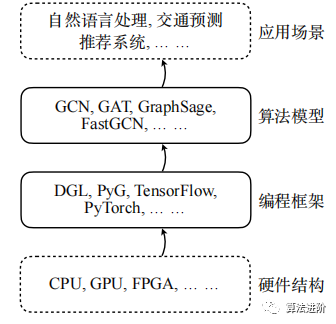
Table 1 lists the relevant surveys in this article. The surveys [29-32] focus on the full graph training mode of GNN models and their applications. However, when the number of nodes or edges is large, the training process is limited by the memory of a single GPU. To address this issue, sampling algorithms support the transition of GNN models from full graph training to mini-batch training and are applied to large-scale data. GNN programming frameworks, combined with deep learning frameworks and graph structure features, improve storage utilization and computational efficiency, promoting large-scale data applications. The surveys [33-34] mainly summarize the progress of GNN programming frameworks. The surveys [36-38] focus on distributed platforms, summarizing and analyzing the progress of distributed GNNs in algorithm models, software frameworks, and hardware platforms.

This article investigates, summarizes, and analyzes GNNs for large-scale applications from two aspects: algorithm models and framework optimization. First, it introduces the fundamental knowledge and typical algorithms of GNNs, then summarizes the GNN models with different granularity sampling strategies, as well as mainstream acceleration frameworks and related technologies. This provides ideas for the subsequent collaborative optimization of frameworks and algorithms in large-scale data applications of GNNs.
The organization of this article is shown in Figure 2:
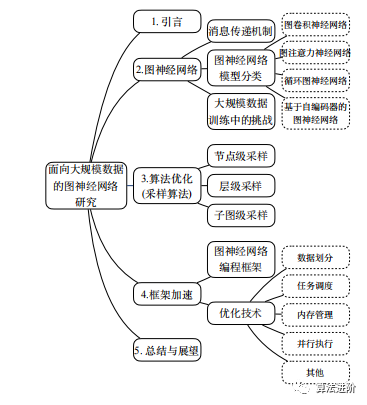
Figure2 Organization of This Article
2 Graph Neural Networks
Graph neural networks (GNNs) are a type of neural network model designed for graph-structured data, combining the advantages of graph computation and neural networks to capture graph structures and abstract node features. Graph computation models excel at capturing topological structures but cannot handle high-dimensional features. Typical neural networks are suitable for Euclidean space data, such as convolutional neural networks for grid data and recurrent neural networks for sequential information. For complex non-Euclidean space graph data, the modeling process requires new processing mechanisms. Currently popular message passing patterns enhance node expressive power by acquiring higher-order neighbor information, including two steps: neighbor aggregation and node updating.
This section starts with the message passing mechanism, introducing the aggregation and updating operations of GNN models, classifying and introducing graph convolutional networks, graph attention networks, gated graph neural networks, and autoencoder-based graph neural networks, analyzing their challenges in large-scale data training, and summarizing these challenges.
2.1 Message Passing Mechanism
2.2 Common Models
Graph Convolutional Network (GCN)..GCN is a common GNN model that implements neighbor node aggregation through convolutional operations. GCN models are divided into spectral domain-based and spatial domain-based categories, where spectral domain methods are based on graph signal analysis and spectral graph theory, while spatial domain methods focus on direct aggregation of neighboring nodes.
In large-scale data training, GCN faces memory shortages and neighbor explosion issues. Mini-batch training can alleviate memory limitations but increases computational and memory consumption. As the number of layers increases, resource consumption grows exponentially.
Graph Attention Network (GAT).GAT is a deep learning model for processing graph-structured data. It introduces an attention mechanism to assign different weights to each node to capture dependencies between nodes. GAT demonstrates efficiency and scalability in GNNs and is widely applied in social networks, recommendation systems, and bioinformatics.
In large-scale data training, both GAT and GCN face memory shortages and neighbor explosion issues. GAT uses attention-weighted aggregation, which consumes more computational and storage resources.
Gated Graph Neural Network (GGNN).Recurrent neural networks (RNNs) are used for modeling sequential information, such as text, user history, and audio/video. Long short-term memory networks (LSTMs) and gated recurrent units (GRUs) are two common forms of RNNs. The GGNN model is based on GRU and targets tasks involving output state sequences, while GCN and GAT models take static graphs as input. GGNN takes time-evolving graphs as input and captures graph structural evolution features through structures like forget gates and update gates.
In large-scale data training, GGNN needs to load the entire adjacency matrix, occupying larger memory. Training involves a significant number of parameters, leading to notable memory challenges. In mini-batch training, the irregularity of graph data increases redundant computations.
Autoencoder-based Graph Neural Network (Structural Deep Network Embedding, SDNE).Autoencoders consist of encoders and decoders, efficiently learning node representations through unsupervised learning. The SDNE model applies autoencoders to graph-structured data, similar to typical autoencoder models, requiring the reduction of reconstruction loss of nodes. Additionally, it considers the similarity between nodes.
SDNE cannot capture high-order associations between nodes and needs to leverage loss functions to capture direct associations between nodes. However, in large-scale data training, memory limitations lead to redundant computations in mini-batch training. Despite using negative sample sampling, the irregularity of graph data still poses challenges.
Table 3 summarizes the challenges faced by GNNs in large-scale data applications based on different training methods (full batch training and mini-batch training) in three aspects: GNN models, graph data structures, and data scale.
Table 3 Challenges of GNNs in Large-Scale Data Applications
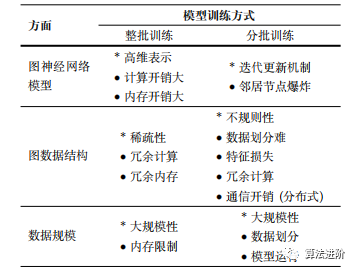
3 GNN Sampling Algorithms
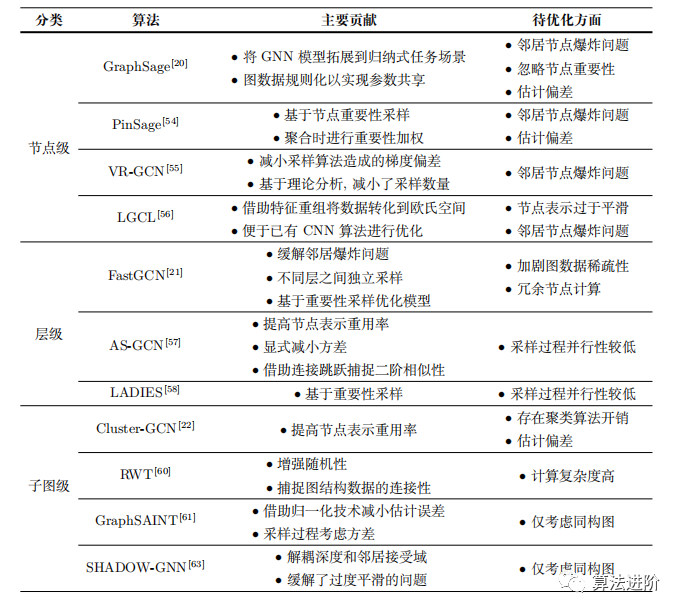
To address the challenges faced by GNNs in large-scale data training, meaningful algorithm optimization work has been undertaken. Most of the work focuses on optimizing data, with the primary method being the use of different granularity sampling algorithms to achieve mini-batch training. These algorithms can be categorized into three types based on sampling granularity: node-based sampling algorithms, layer-based sampling algorithms, and subgraph-based sampling algorithms.
3.1 Node-based Sampling Algorithms
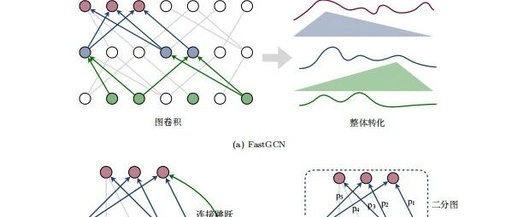
GraphSage.GraphSage employs node sampling for representation learning, optimizing model parameters. As shown in Figure 3(b), for the target node, a fixed number of neighboring nodes are randomly sampled, and feature aggregation is performed using aggregation functions, learning through backpropagation. By optimizing the model, new data representations are achieved, and the irregular graph structure data is regularized through random node sampling algorithms, achieving parameter sharing.
PinSage.The PinSage algorithm combines random walks and graph convolution operations for large-scale recommendation systems. It constructs a computational graph through node sampling, capturing graph structural features and enhancing the scalability of graph convolutional neural network models on large-scale data. It proposes an importance-based node sampling algorithm, as shown in Figure 3(c), evaluating node importance using random walk strategies, selecting the top k most important nodes for sampling, and performing importance weighting during aggregation.
VR-GCN.VR-GCN is a new sampling algorithm that addresses the parameter sharing problem in large-scale GNNs, ensuring convergence through variance reduction, and proving that the sampling scale does not affect local optimal performance. As shown in Figure 3(d), for the target node, VR-GCN samples only two nodes, using historical activated nodes to reduce variance, significantly decreasing the bias and variance of estimated gradients. Compared to considering all neighboring nodes, VR-GCN only considers two neighboring nodes, greatly reducing the time complexity and memory overhead of model training.
LGCL.LGCL structures graph data to meet the requirements of convolution operations, transforming irregular graph structure data into Euclidean space through node feature reorganization, facilitating optimization using CNN algorithms. However, the reorganization method based on significant features somewhat undermines the diversity of node features, exacerbating the problem of over-smoothing node representations. As illustrated in Figure 3(e), the sampling mean aggregation method leads to node feature values approaching the maximum corresponding feature value, ultimately causing all node representations to become similar, exacerbating the over-smoothing problem of graph convolutional networks.
Summary.To address the limitations of direct training models in GNNs, GraphSage proposes a node-based sampling algorithm that adapts to inductive tasks by randomly sampling first-order and second-order neighbors. PinSage introduces an importance-based sampling algorithm and performs importance weighting during node aggregation. VR-GCN focuses on the convergence of sampling algorithms, improving algorithm convergence by reducing the bias and variance of gradient estimates. LGCL filters and reorganizes features to form new nodes for aggregation.
3.2 Layer-based Sampling Algorithms
FastGCN.FastGCN transforms the graph convolution operation into a probabilistic distribution integral form, as shown in Figure 4(a), and uses the Monte Carlo method to estimate the integral value, addressing the time and memory overhead issues in large-scale data training of GNNs. FastGCN employs hierarchical sampling to avoid neighbor node explosion and conducts model training based on the sampled loss function and gradient function, while optimizing performance through importance sampling.
AS-GON.AS-GON is an adaptive hierarchical sampling algorithm that avoids neighbor node explosion in GCN by fixing the number of sampled nodes per layer. Sampling nodes in the lower layer based on the sampling results of the upper layer allows as many lower-layer neighboring nodes to be shared by upper-layer nodes as possible. AS-GON also captures second-order similarity through connection jumps, utilizing connection jump strategies to obtain second-order neighbor feature information, propagating high-order neighbor feature information without additional sampling overhead.
LADIES.LADIES is a new sampling algorithm aimed at addressing challenges in both node-based and layer-based sampling algorithms. As illustrated in Figure 4(d), this algorithm constructs a bipartite graph based on upper-layer nodes and their neighboring nodes, calculating importance scores as sampling probabilities and sampling a fixed number of neighboring nodes as lower-layer nodes based on these probabilities. By iteratively constructing the entire computational graph, it effectively reduces computational and memory overhead.
Summary.FastGCN estimates integral values through hierarchical sampling to avoid neighbor node explosion but faces issues with sparse connections and redundant nodes. AS-GCN ensures convergence through explicit variance reduction and captures second-order associations. LADIES constructs adjacent two-layer nodes based on bipartite graphs for hierarchical importance sampling, alleviating the neighbor node explosion issue, but global node reuse is limited.
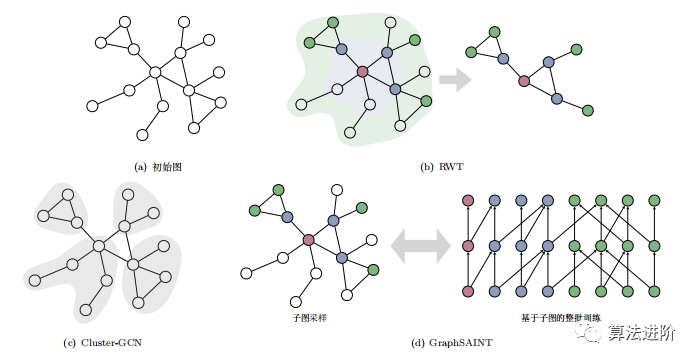
3.3 Subgraph-based Sampling Algorithms
Cluster-GCN.Cluster-GCN improves the computational efficiency of GCN’s mini-batch training through subgraph sampling algorithms. By using the clustering-aware partitioning algorithm Metis, nodes are divided into c blocks, and the adjacency matrix is transformed into diagonal matrices A and B. The representation function of GCN is decomposed into different clustering blocks, and random combinations of blocks are used to alleviate the issues of edge omission and estimation errors. In mini-batch training, multiple clustering blocks are randomly selected for each batch rather than using a single block as training data.
RWT.RWT is a layer-wise random walk training strategy designed to address time and space overhead issues in Cluster-GCN for large-scale graph applications. It implements mini-batch training through subgraph sampling, constructing GNN models for training in each batch. The sampling strategy considers both randomness and graph structural connectivity, employing a layer-wise expansion approach to sample from neighboring nodes of the current subgraph and update the subgraph until a threshold is reached. RIWT has been validated for effectiveness on GCN and GAT.
GraphSAINT.GraphSAINT is a sampling-based GNN model that first samples subgraphs and then constructs network models, eliminating mini-batch training bias and reducing mini-batch variance. First, it estimates the sampling probabilities of nodes and edges, then performs subgraph sampling in each training batch and constructs a complete GON model for training. Normalization methods eliminate bias while optimizing sampling algorithms through random walk strategies.Zeng et al. proposed GraphSAINT, which improves accuracy through bias elimination and error reduction. They proposed a parallel training framework that enhances program parallelism through subgraph sampling mini-batch training. The parallelization between and within samplers theoretically provides near-linear speedup. In terms of feature propagation, it improves cache utilization and reduces communication overhead through data partitioning. Additionally, they proposed a runtime scheduler to optimize parallel performance through reordering operation sequences and adjusting mini-batch graphs.
SHADOW-GNN.SHADOW-GNN is a GNN model designed to address the challenges posed by large-scale data and alleviate over-smoothing issues. By decoupling the association between the node acceptance region and the depth of the GNN, it achieves deep network expressive capabilities while avoiding over-smoothing. SHADOW-GNN employs subgraph sampling strategies to form different subgraphs, then applies GNN models of arbitrary depth on these subgraphs to obtain node representations.
Summary.Cluster-GCN improves node utilization through node clustering, as shown in Figure 5(c); RWT employs random walk strategies for layer-wise expansion of subgraphs, as shown in Figure 5(b); GraphSAINT focuses on reducing estimation bias and variance to improve model performance; SHADOW-GNN enhances model scalability and alleviates over-smoothing issues through graph sampling strategies, as shown in Figure 5(d).
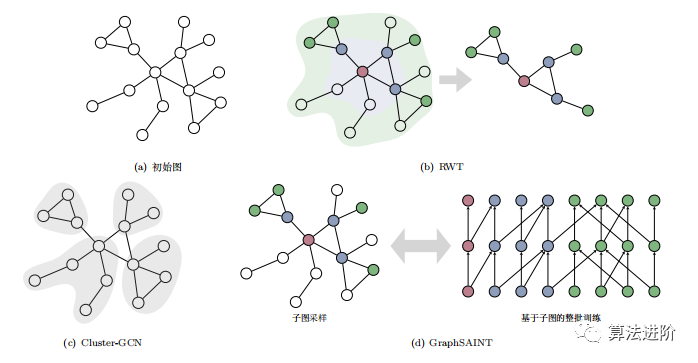
Figure 5 Subgraph-based Sampling Algorithms
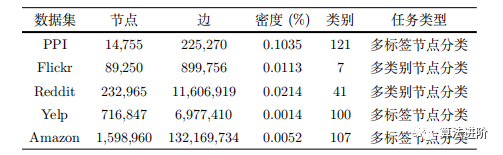
Zeng et al. compared the accuracy of four sampling algorithms on node classification tasks across five datasets (Table 4), with performance comparison results shown in Table 5. The subgraph-based sampling algorithms performed better across different datasets, with higher micro F1 scores and lower variance. The node classification accuracy of GraphSage is close to that of subgraph-based sampling algorithms on datasets such as Flickr, Reddit, Yelp, and Amazon, but with longer training times.
Table 4 Dataset Statistics
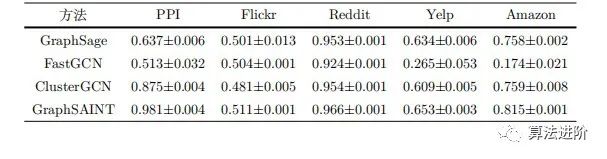
To address the challenges in large-scale data training, this section summarizes different granularity sampling algorithms (as shown in Table 6), including node-level, layer-level, and subgraph-level sampling algorithms. These algorithms alleviate memory limitations in large-scale data training to some extent, increase model scalability, and improve model convergence through importance sampling, variance reduction, and random combinations. However, current sampling algorithms primarily optimize based on static homogeneous graphs, ignoring the complex features of graph data in real applications, such as heterogeneity, dynamics, and power-law distributions.
Table 6 Summary of Sampling Algorithms
4 Graph Neural Network Framework
The computation process of GNNs involves irregular memory access and complex feature computations, and traditional frameworks perform poorly in graph computations. To address this issue, researchers have proposed programming frameworks for GNNs and explored optimization techniques, laying the foundation for running and optimizing large-scale GNN models.
Table 7 GNN Programming Frameworks
4.2 Framework-Related Optimization Techniques
Table 8 Framework-Related Optimization Techniques for GNNs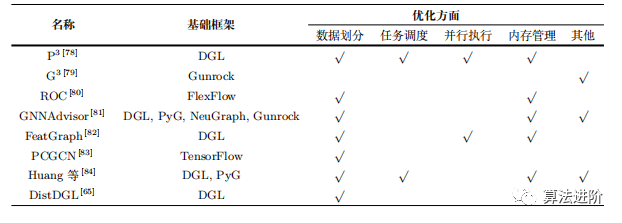
5 Summary and Outlook
Common GNN Models and Their Challenge Analysis. This article first introduces four common GNN models: graph convolutional networks, graph attention networks, gated graph neural networks, and autoencoder-based graph neural networks, analyzing the challenges they face in large-scale data applications and summarizing and analyzing model-layer-related challenges. Then, it summarizes and analyzes relevant research from the perspectives of algorithm models and programming frameworks.
Algorithm Models.To address the challenges brought by large-scale data in GNN model training, most optimization work focuses on sampling algorithms. This article categorizes existing work based on sampling granularity into node-based, layer-based, and subgraph-based sampling algorithms. For each category of sampling algorithm, it introduces the main associated models and analyzes them. Finally, a comprehensive summary and analysis are conducted.
Programming Frameworks.This article first summarizes mainstream programming frameworks like DGL and PyG. It then categorizes existing optimization techniques into five categories: data partitioning, task scheduling, parallel execution, memory management, and others. For each category, it briefly introduces the optimization objectives and lists specific optimization strategies. Finally, a comprehensive summary and analysis are conducted.
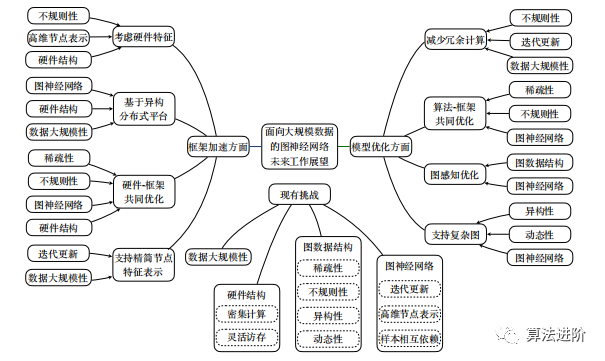
Outlook.This article summarizes the related progress of GNN optimization for large-scale data, covering both model optimization and framework acceleration aspects. Below, we will look forward to future work from these two aspects, as detailed in Figure 6: