Click the blue text to follow us for more knowledge sharing.
01
Forward Propagation
To explain the forward propagation of neural networks, we will use a simple fully connected three-layer neural network as shown in the figure below:
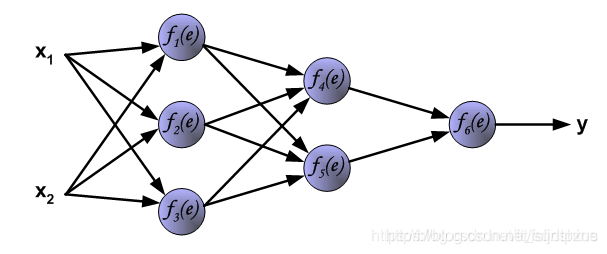
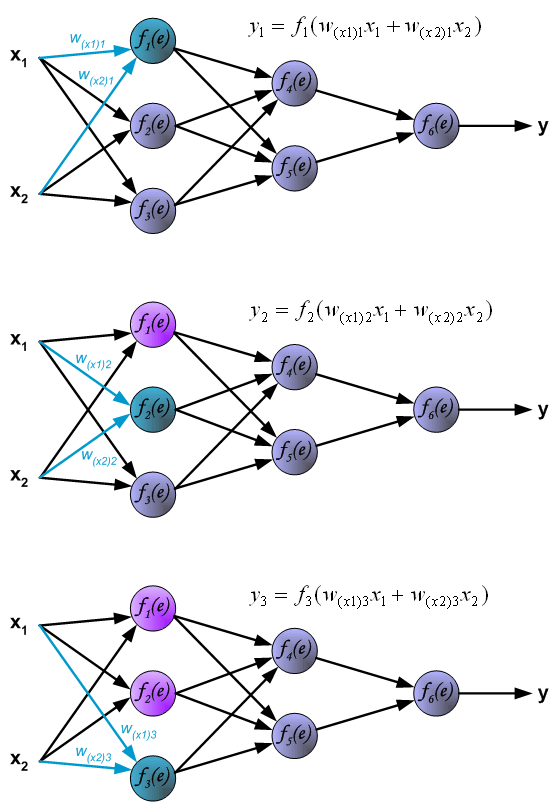
The neural network consists of layers of neurons (one column is considered a layer of the neural network). In forward propagation, each neuron in each layer is connected to all neurons in the previous layer or to the input data. For example, in the figure, f1(e) is connected to x1 and x2. Therefore, during computation, the output of each neuron = the sum of the functions of the previous layer before applying the activation function. For instance, the output y1 of f1(e) is calculated as y1 = (w(x1)x1 + w(x2)x2)
Where w is the weight, and f(e) represents the activation function; bias is not included in this example.
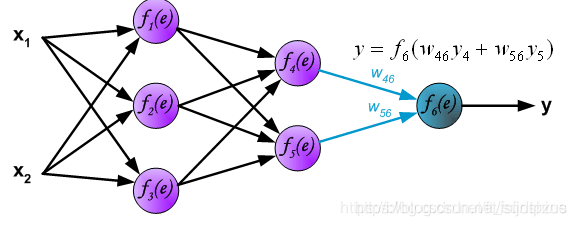
Then, f1, f2, and f3 are fully connected as inputs to the neurons in the next layer, and f4, f5 as inputs to the final layer of neurons, ultimately producing the output y value.
02
Backward Propagation Principle
The Backpropagation algorithm (BP algorithm) is a learning algorithm suitable for multi-layer neural networks. The learning process of the BP algorithm consists of the forward propagation process and the backward propagation process.
In the forward propagation process, as mentioned earlier, if the predicted value y does not match the actual value, the square sum of the output and the expected error is taken as the loss function.
The loss function from the forward propagation is then passed into the backward propagation process, where the partial derivatives of the loss function with respect to each neuron’s weights and biases are calculated layer by layer, serving as the gradient of the objective function concerning the weights and biases. Based on this computed gradient, the weights w and biases b are modified, completing the network’s learning during the weight modification process. The network learning ends when the error reaches the desired value.
Assuming you have the following network layer: the first layer is the input layer with two neurons i1 and i2, and bias b1; the second layer is the hidden layer with two neurons h1 and h2 and bias b2; the third layer is the output layer o1 and o2, with weights wi marked on each line connecting the layers, and we assume the activation function is the sigmoid function. Now we assign initial values:
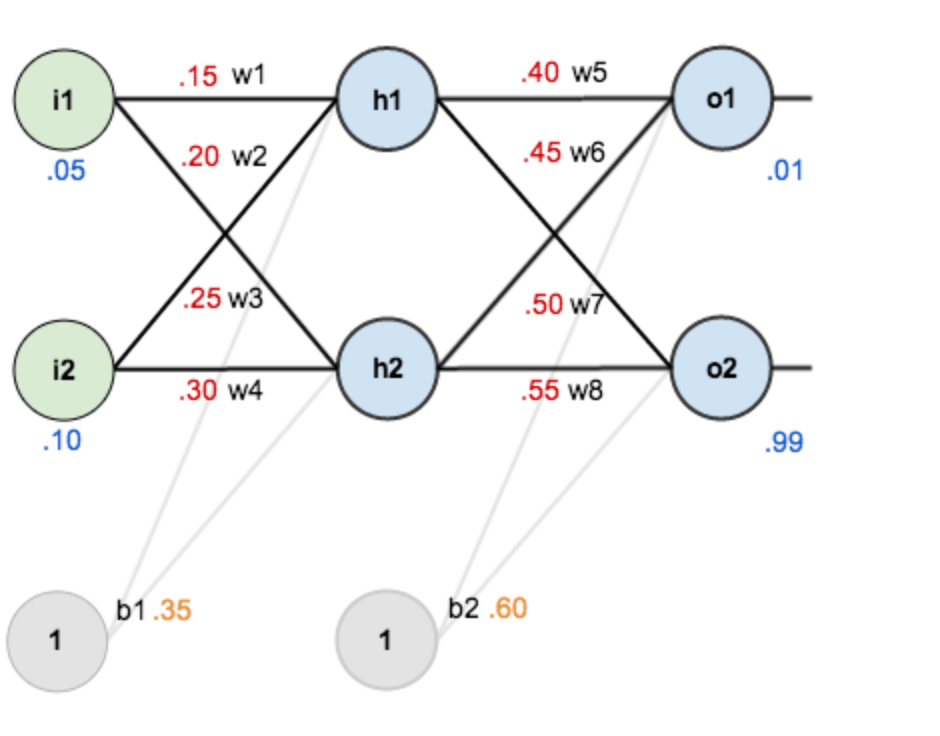
Given input data, weights, biases, and activation functions, according to the steps of forward propagation, the output value is [0.75136079, 0.772928465], which is still far from the actual values [0.01, 0.99]. Now we perform backward propagation on the error, updating the weights and biases and recalculating the output.
03
Backward Propagation Steps
Taking the update of weights as an example:
1
Calculate Total Error
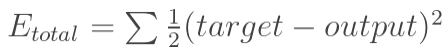

2
Weight Update from Hidden Layer to Output Layer:
Taking weight parameter w5 as an example, if we want to know how much influence w5 has on the overall error, we can use the overall error to take the partial derivative with respect to w5: (Chain Rule)
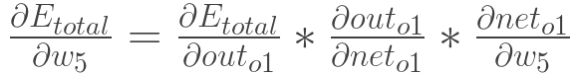
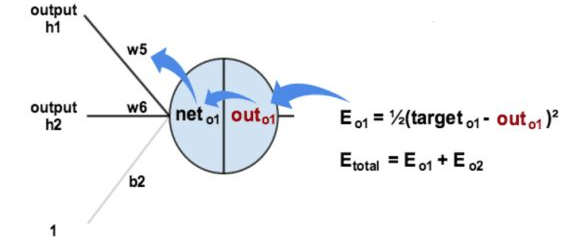
Substituting data:

We can obtain:

Finally, we update the value of w5:
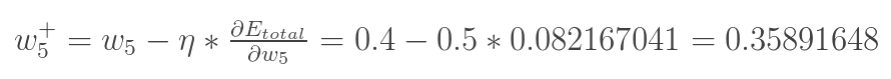
(where n is the learning rate, controlling the step size for weight updates, here we take 0.5)
Similarly, we can update w6, w7, w8:
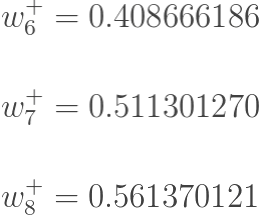
3
Weight Update from Hidden Layer to Hidden Layer
The method is actually similar to what was mentioned above, but one thing needs to change. When calculating the total error’s partial derivative with respect to w5, it was from out(o1)—->net(o1)—->w5, but for the weight update between hidden layers, it is out(h1)—->net(h1)—->w1, and out(h1) will receive errors from E(o1) and E(o2) from both places, so both need to be calculated.
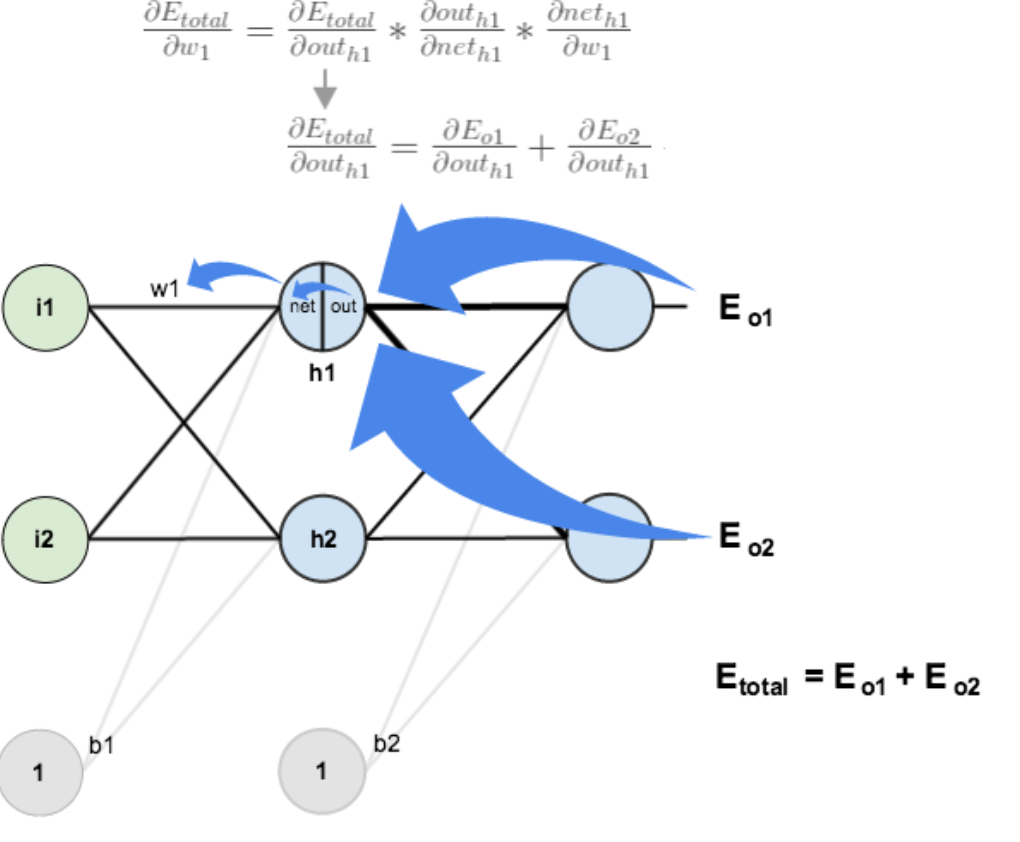
Similar to the above calculation process, substituting data gives:
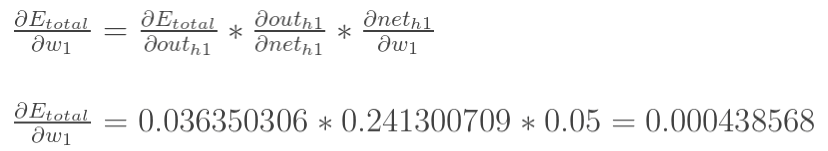
Updating the weight of w1:
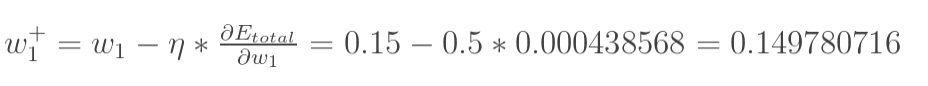
Similarly, we can obtain the weights of w2, w3, and w4:
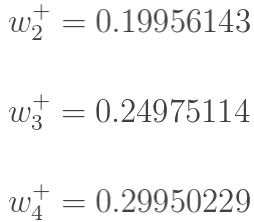
Thus, the error backpropagation method is completed, and finally, we recalculate the updated weights, iterating continuously until the total error is reduced to our expected range.
Note: This article is for knowledge sharing purposes only and is provided for reference. If there are any infringements, it will be deleted.
1. Original link: https://blog.csdn.net/fsfjdtpzus/article/details/106256925
2. Original link: https://blog.csdn.net/qq_29407397/article/details/90599460
Recommended Reading

1. Liu Duzhou on common prescriptions for palpitations and heart discomfort
2. Swing hand patting to relieve hunchback, lumbar disc herniation, lumbar muscle strain, without spending a penny~
3. [Health and Wellness] How to treat “winter diseases” in the summer? It is already into the summer heat, and there are nine questions you must know for treating winter diseases in summer!
4. Basic knowledge of Convolutional Neural Networks
5. Neural Network Algorithms

Ancient and Modern Medical Case Cloud Platform
Providing over 400,000 ancient and modern medical case search services
Supports manual, voice, OCR, and batch structured input of medical cases
Designed with nine analysis modules, closely aligned with clinical needs
Supports collaborative analysis of massive medical cases on the platform and personal medical cases
Cloud Medical Case APP
Mobile terminal for real scene medical case collection on the Ancient and Modern Medical Case Cloud Platform
High-precision OCR recognition and intelligent voice extraction technology
Real-time synchronization to the Ancient and Modern Medical Case Cloud Platform
Data structured, standardized, and data mining in one step
Android users can directly scan the QR code on the right or search for “Cloud Medical Case APP” in the application treasure to download


Scan the QR code to follow us
China Academy of Chinese Medical Sciences Institute of Chinese Medicine Information Research
Intelligent R&D Center for Traditional Chinese Medicine Health
Big Data R&D Department
Phone: 010-64089619
QQ: 2778196938
Client download: www.yiankb.com